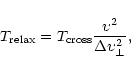 |
(1) |
The relaxation time for a single star can be defined as the time
necessary for two-body encounters to change its velocity, or energy, by
an amount of the same order as the initial velocity, or energy,
i.e. the time in which the memory of the initial values is lost. Thus
for the velocity we have
 |
(5) |
The appropriate values of
![]() and
and
![]() in
the above equations have
been discussed at length in the literature. Chandrasekhar (1942)
argued that
in
the above equations have
been discussed at length in the literature. Chandrasekhar (1942)
argued that
![]() is the value of b for which the
angular deflection
of the star is equal to
is the value of b for which the
angular deflection
of the star is equal to
![]() .
The value of
.
The value of
![]() has been subject to considerable controversy. Chandrasekhar (1942),
Kandrup (1980) and Smith (1992) have opted for a
has been subject to considerable controversy. Chandrasekhar (1942),
Kandrup (1980) and Smith (1992) have opted for a
![]() of
the order of the mean inter-particle distance, while others
(e.g. Spitzer & Hart 1971; Farouki & Salpeter
1982; Spitzer 1987)
used for
of
the order of the mean inter-particle distance, while others
(e.g. Spitzer & Hart 1971; Farouki & Salpeter
1982; Spitzer 1987)
used for
![]() a characteristic radius of the system. The
numerical simulations of Farouki & Salpeter (1994) argue
in favour of the latter. This is further corroborated by the
results of Theis (1998).
a characteristic radius of the system. The
numerical simulations of Farouki & Salpeter (1994) argue
in favour of the latter. This is further corroborated by the
results of Theis (1998).
Using the estimates
![]() ,
,
![]() and
assuming virial equilibrium, so that we can use for the velocity the
estimate
and
assuming virial equilibrium, so that we can use for the velocity the
estimate
![]() ,
we find
(Binney & Tremaine 1987)
,
we find
(Binney & Tremaine 1987)
It is clear that, for the number of particles used in present-day
simulations of collisionless systems and the appropriate values of the
softening, N is considerably larger than
![]() .
Since,
however, only the logarithms of these quantities enter in Eqs. (6) and (7), the differences in the estimates of the relaxation
times differ, for commonly used values of N, by less than a factor of
2. Equation (7)
is more appropriate, since it includes the softening. Often a
coefficient g is introduced in the Coulomb logarithm,
i.e.
.
Since,
however, only the logarithms of these quantities enter in Eqs. (6) and (7), the differences in the estimates of the relaxation
times differ, for commonly used values of N, by less than a factor of
2. Equation (7)
is more appropriate, since it includes the softening. Often a
coefficient g is introduced in the Coulomb logarithm,
i.e.
![]() .
Giersz & Heggie (1994) estimated
that the most appropriate value of g is 0.11. They also
compiled in their Table 2 the values given by several other
authors. They are all between 0.11 and 0.4. Independent of what is
chosen for the Coulomb logarithm, equations such as (6)
or (7) argue that even for a moderately low number
of particles, of the order of say a few thousands, the relaxation time
is comfortably high, of the order of, or higher than, 40 crossing
times.
.
Giersz & Heggie (1994) estimated
that the most appropriate value of g is 0.11. They also
compiled in their Table 2 the values given by several other
authors. They are all between 0.11 and 0.4. Independent of what is
chosen for the Coulomb logarithm, equations such as (6)
or (7) argue that even for a moderately low number
of particles, of the order of say a few thousands, the relaxation time
is comfortably high, of the order of, or higher than, 40 crossing
times.
Copyright ESO 2001