A&A 487, 975-991 (2008)
DOI: 10.1051/0004-6361:200809426
T. A. van Kempen1 - S. D. Doty2 - E. F. van Dishoeck1,3 - M. R. Hogerheijde1 - J. K. Jørgensen4
1 - Leiden Observatory, Leiden University, PO Box 9513, 2300 RA Leiden, The Netherlands
2 - Department of Physics and Astronomy, Denison
University, Olin 109 Granville, OH 43023, USA
3 - Max-Planck Institut für Extraterrestrische
Physik (MPE), Giessenbachstr. 1, 85748 Garching, Germany
4 -
Argelander-Institut für Astronomie, Universität Bonn,
Auf dem Hügel 71, 53121 Bonn, Germany
Received 18 January 2008 / Accepted 3 April 2008
Abstract
Context. Within low-mass star formation, water vapor plays a key role in the chemistry and energy balance of the circumstellar material. The Herschel Space Observatory will open up the possibility to observe water lines originating from a wide range of excitation energies.
Aims. Our aim is to simulate the emission of rotational water lines from envelopes characteristic of embedded low-mass protostars. A large number of parameters that influence the water line emission are explored: luminosity, density, density slope, and water abundances.
Methods. Both dust and water emission are modeled using full radiative transfer in spherical symmetry. The temperature profile is calculated for a given density profile. The H2O level populations and emission profiles are in turn computed with a non-LTE line code. The results are analyzed to determine the diagnostic value of different lines, and are compared with existing observations.
Results. Lines can be categorized in: (i) optically thick lines, including ground-state lines, mostly sensitive to the cold outer part; (ii) highly excited (
![]() -250 K) optically thin lines sensitive to the abundance in the hot inner part; and (iii) lines which vary from optically thick to thin depending on the abundances. Dust influences the emission of water significantly by becoming optically thick at the higher frequencies, and by pumping optically thin lines.
-250 K) optically thin lines sensitive to the abundance in the hot inner part; and (iii) lines which vary from optically thick to thin depending on the abundances. Dust influences the emission of water significantly by becoming optically thick at the higher frequencies, and by pumping optically thin lines.
Conclusions. A good physical model of a source, including the correct treatment of dust, is a prerequisite for inferring the water abundance structure and possible jumps at the evaporation temperature from observations. The inner warm (T>100 K) envelope can be probed by highly excited lines, while a combination of excited and spectrally resolved ground state lines probes the outer envelope. Observations of H218O lines, although weak, provide even stronger constraints on abundances.
Key words: stars: pre-main sequence - circumstellar matter - stars: formation - ISM: molecules - submillimeter
Low-mass (
![]() )
young stellar objects (YSOs) form
through gravitational collapse of cloud cores. Most of their mass is
accreted over periods of less than 106 years
(André et al. 2000; Myers et al. 2000). These early stages of low-mass star
formation, the so-called Class 0 and Class I stages, are characterized
by the presence of centrally condensed envelopes that veil the
central protostars and disks (Lada 1987; André et al. 1993). The envelopes also contain
most of the mass (
)
young stellar objects (YSOs) form
through gravitational collapse of cloud cores. Most of their mass is
accreted over periods of less than 106 years
(André et al. 2000; Myers et al. 2000). These early stages of low-mass star
formation, the so-called Class 0 and Class I stages, are characterized
by the presence of centrally condensed envelopes that veil the
central protostars and disks (Lada 1987; André et al. 1993). The envelopes also contain
most of the mass (![]() -
-
![]() )
of the total system
until the emergence of the central star and disk
(Adams et al. 1987; Shirley et al. 2000; Jørgensen et al. 2002). Water plays a pivotal role in
these early evolutionary stages. First, the high dipole moment of
H2O makes its rotational lines excellent coolants of warm gas in
the inner region of protostellar envelopes, allowing material to
continue collapsing at higher temperatures
(Goldsmith & Langer 1978; Neufeld & Kaufman 1993; Ceccarelli et al. 1996). Second, water is one of
the dominant reservoirs of the non-refractory oxygen budget in dense
clouds (van Dishoeck et al. 1993). The partitioning of gaseous oxygen
between H2O, OH and O, as well as the ratio between H2O gas and
ice, affect the chemistry of all other oxygen-containing molecules
including the complex organics (Charnley et al. 1992).
The evaporation point of H2O ice in interstellar space is
around 100 K (Fraser et al. 2001), so only the small warm inner
regions of protostellar envelopes are likely to contain fractional
abundances of water vapor as high as 10-4 with respect to H2,
perhaps even exceeding that of CO
(e.g., van Dishoeck & Blake 1998; Ceccarelli et al. 1996; Boonman et al. 2003). In colder
regions, water is the main ingredient of icy grain mantles as shown by
infrared spectroscopy
(e.g., Pontoppidan et al. 2004; Boogert et al. 2002; Whittet et al. 1983; Smith et al. 1989), with
gas-phase water abundances that are orders of magnitudes lower. This abundance
jump makes water an excellent tracer of warm, dense gas and a unique
probe into the inner region close to the forming star.
)
of the total system
until the emergence of the central star and disk
(Adams et al. 1987; Shirley et al. 2000; Jørgensen et al. 2002). Water plays a pivotal role in
these early evolutionary stages. First, the high dipole moment of
H2O makes its rotational lines excellent coolants of warm gas in
the inner region of protostellar envelopes, allowing material to
continue collapsing at higher temperatures
(Goldsmith & Langer 1978; Neufeld & Kaufman 1993; Ceccarelli et al. 1996). Second, water is one of
the dominant reservoirs of the non-refractory oxygen budget in dense
clouds (van Dishoeck et al. 1993). The partitioning of gaseous oxygen
between H2O, OH and O, as well as the ratio between H2O gas and
ice, affect the chemistry of all other oxygen-containing molecules
including the complex organics (Charnley et al. 1992).
The evaporation point of H2O ice in interstellar space is
around 100 K (Fraser et al. 2001), so only the small warm inner
regions of protostellar envelopes are likely to contain fractional
abundances of water vapor as high as 10-4 with respect to H2,
perhaps even exceeding that of CO
(e.g., van Dishoeck & Blake 1998; Ceccarelli et al. 1996; Boonman et al. 2003). In colder
regions, water is the main ingredient of icy grain mantles as shown by
infrared spectroscopy
(e.g., Pontoppidan et al. 2004; Boogert et al. 2002; Whittet et al. 1983; Smith et al. 1989), with
gas-phase water abundances that are orders of magnitudes lower. This abundance
jump makes water an excellent tracer of warm, dense gas and a unique
probe into the inner region close to the forming star.
Observations of interstellar gas-phase water from the ground are
limited by the large amounts of water vapor in the Earth's atmosphere.
Water maser lines at radio wavelengths longward of 3 mm (100 GHz), such as at
22 GHz, are readily seen, even from low-mass embedded YSOs
(e.g., Furuya et al. 2003; Park & Choi 2007), but are constrained to small hot spots
and are often variable in nature (Felli et al. 2007). They provide little
information about the general physical and chemical evolution during
star formation (Elitzur et al. 1989). One of the few exceptions of a
non-masing water line observable from the ground is the 183 GHz
J=313-202 transition, which can be used to trace widespread
water emission under exceptional conditions
(e.g., Cernicharo et al. 1996; Doty 2000; Cernicharo et al. 1990).
Observations of deuterated water can also be done from the ground, in
particular through the HDO 101-000 464 GHz, 312-221225 GHz, and 211-212 241 GHz lines
(e.g., Turner et al. 1975; Jacq et al. 1990; Helmich et al. 1996; Stark et al. 2004; Parise et al. 2005) and the
D2O 110-101 316 GHz line (Butner et al. 2007), but the large
uncertainties in the D/H ratio owing to fractionation make such
observations a poor tracer of water itself. The H218O
isotopologue can be detected as well, but only through its high
excitation temperature (
![]() K) 313-220transition at 203 GHz (e.g., Jacq et al. 1988; van der Tak et al. 2006; Gensheimer et al. 1996).
K) 313-220transition at 203 GHz (e.g., Jacq et al. 1988; van der Tak et al. 2006; Gensheimer et al. 1996).
To observe water emission lines systematically for a wide range of
energy states, one has to turn to space-based observatories. Gaseous
water has been detected in a number of starforming regions using the
Infrared Space Observatory (ISO), the Sub-millimeter Wave Astronomy
Satellite (SWAS), and ODIN (e.g., Ristorcelli et al. 2005; Nisini et al. 2002; Harwit et al. 1998; Bergin & Snell 2002; Maret et al. 2002; Boonman et al. 2003; Cernicharo & Crovisier 2005; Bergin & Melnick 2005; Snell et al. 2000; Nisini et al. 1999; Helmich et al. 1996; Ceccarelli et al. 1999). However,
due to large beams, low spectral resolution, or a combination of both,
such observations were unable to accurately resolve the water
abundance profile and trace the origin of the water emission,
especially for low-mass YSOs. Two instruments onboard the Herschel
Space Observatory![]() can be used
for future observations of rotational water lines at unprecedented
sensitivity, resolution and spectral coverage
(Ceccarelli et al. 2001). The Heterodyne Instrument for the Far
Infrared (HIFI) (de Graauw & Helmich 2001) and Photodetector Array
Camera and Spectrometer (PACS) (Poglitsch et al. 2001) provide high
spectral (up to 125 kHz) and spatial (20'' at 1 THz) resolution,
which will allow a thorough analysis of water emission through a much
wider range of observable transitions. In addition, the high
sensitivity of the instrument will allow observations of various lines
at low abundance, such as the optically thin isotopologues of water, in particular
H218O. However, to infer abundances from such observations,
detailed radiative transfer calculations are needed.
can be used
for future observations of rotational water lines at unprecedented
sensitivity, resolution and spectral coverage
(Ceccarelli et al. 2001). The Heterodyne Instrument for the Far
Infrared (HIFI) (de Graauw & Helmich 2001) and Photodetector Array
Camera and Spectrometer (PACS) (Poglitsch et al. 2001) provide high
spectral (up to 125 kHz) and spatial (20'' at 1 THz) resolution,
which will allow a thorough analysis of water emission through a much
wider range of observable transitions. In addition, the high
sensitivity of the instrument will allow observations of various lines
at low abundance, such as the optically thin isotopologues of water, in particular
H218O. However, to infer abundances from such observations,
detailed radiative transfer calculations are needed.
Several modeling efforts have been carried out to analyze the observed water lines, based either on models of shocks at high and low velocities (e.g., Giannini et al. 2001; Nisini et al. 2002; Kaufman & Neufeld 1996) or on thermal emission from the envelope itself (e.g., Maret et al. 2002; Boonman et al. 2003). As pointed out by van der Tak et al. (2006), the high water abundance combined with its high dipole moment and its susceptibility to far-infrared emission from dust results in high optical depths make this molecule particularly difficult to model. As a result, no systematic parameter studies have been carried out yet We present here a parameter study of the water emission from low-mass protostellar envelopes using a full radiative transfer method including the effects of dust that is applied to realistic physical models of low-mass YSOs. Specific predictions for Herschel are made by convolving the computed emission with the Herschel observing beams. Poelman & van der Tak (2007) present similar models for high-mass protostars.
This paper is organized as follows. Section 2 presents the physical and molecular parameters necessary to accurately model water. Section 3 takes an in-depth look at a single Class 0 source, L 483, and explores the effects of possible water abundance profiles. Section 4 presents the results from the range of parameters that influence water emission. Section 5 investigates the influence of dust on water line fluxes and profiles, which is often ignored. Section 6 gives an analysis of a selected sample of observed water lines from ISO, SWAS, and ODIN to test the models and to infer implications for observations with future instruments such as HIFI and PACS. Final conclusions and recommendations can be found in Sect. 7.
The modeling has been carried out in two stages. First, the dust radiative transfer is calculated for a given power-law density profile (Sect. 2.1). This produces dust temperature profiles for given density structures. Subsequently, water level populations and line emission profiles are modeled using the line radiative transfer code RATRAN (Sect. 2.2) (Hogerheijde & van der Tak 2000), with the assumption that the gas temperature is equal to that of the dust. For an overview of the steps, see van Dishoeck (2003) (Fig. 2). Our method refers to the ``empirical method'' presented there. See Table 1 for an overview of the parameters.
Table 1: Parameters for low-mass protostellar envelopes.
Our protostellar envelope models are taken to be spherically
symmetric, with the protostar located at the center. It has been shown
that this assumption is valid for analyzing both the continuum
and line emission down to scales of a few hundred AU
(e.g., Jørgensen et al. 2005; Shirley et al. 2000; Jørgensen et al. 2002; Schöier et al. 2002). The
density n at radius r within the protostellar envelope is
described by
| n(r)=n0(r/r0)-p, | (1) |
Both the gas and dust temperatures inside the envelope are also often described by a power-law profile. However, this approximation fails at small radii where the dust becomes optically thick (e.g., Doty & Leung 1994; Jørgensen et al. 2002;Young & Evans 2005). The actual temperature structure depends on a combination of the density structure and the central source luminosity, and a dust radiative transfer calculation is needed to determine it. The radiation is produced by the energy released through accretion of material onto the protostar.
Table 2: The masses and inner radii of the model envelopes.
| |
Figure 1:
Example of the physical structure of a model envelope with the density (solid), temperature (dashed), and abundance (dotted) displayed versus radius. The adopted parameters are
|
| Open with DEXTER | |
The continuum radiative transfer through the envelope was calculated
using the spherically symmetric dust radiative transfer code DUSTY
(Ivezic & Elitzur 1997). DUSTY is a scale-free 1D code that uses the ratio Y of the outer over inner radius,
![]() /
/
![]() ,
the
dust opacity
,
the
dust opacity ![]() at 100
at 100 ![]() m, the temperature at
m, the temperature at
![]() ,
and the power-law index of the density profile p as its
variables. Results are then scaled by using the luminosity and
distance of specific sources. The inner edge of our envelope
,
and the power-law index of the density profile p as its
variables. Results are then scaled by using the luminosity and
distance of specific sources. The inner edge of our envelope
![]() was set at the radius where the temperature of the
envelope reaches 250 K. Material closer to the star is assumed to be
located in a disk, which is not taken into account. In addition, we
assume that the disk has no influence on the temperature and density
distribution of the envelope. The exact inner radius in AU depends on
the luminosity, which differs for each model, and
was set at the radius where the temperature of the
envelope reaches 250 K. Material closer to the star is assumed to be
located in a disk, which is not taken into account. In addition, we
assume that the disk has no influence on the temperature and density
distribution of the envelope. The exact inner radius in AU depends on
the luminosity, which differs for each model, and
![]() is
typically a few tens of AU, much smaller than the
Herschel beams (see Table 2). In all our models, Y is
taken to be 200. Values of
is
typically a few tens of AU, much smaller than the
Herschel beams (see Table 2). In all our models, Y is
taken to be 200. Values of
![]() are a few thousand to ten
thousand AU, greater than the Herschel beam (20'' at 1113 GHz) at all
but the lowest frequencies, but generally less than the values
given in Jørgensen et al. (2002). The adopted dust opacity's are the
often-used OH tables, Col. 5 of Ossenkopf & Henning (1994)
throughout. Figure 1 shows a typical temperature and
density profile.
are a few thousand to ten
thousand AU, greater than the Herschel beam (20'' at 1113 GHz) at all
but the lowest frequencies, but generally less than the values
given in Jørgensen et al. (2002). The adopted dust opacity's are the
often-used OH tables, Col. 5 of Ossenkopf & Henning (1994)
throughout. Figure 1 shows a typical temperature and
density profile.
![\begin{figure}
\par\includegraphics[scale=0.6]{images/combined1.ps}\end{figure}](/articles/aa/full/2008/33/aa09426-08/Timg44.gif) |
Figure 2:
Contour plots of the integrated water line intensity for the L 483 models, plotted as functions of
|
| Open with DEXTER | |
The gas temperature is taken to be equal to the dust temperature for
the entire spatial extent of our model, and the gas:dust mass ratio is
taken to be 100:1. Warm dense gas can efficiently cool through the
emission of excited molecular and atomic lines such as CO, H2O, OH,
and [O I] (Giannini et al. 2001). Water can also heat the gas through
far-infrared pumping followed by collisional de-excitation
(e.g., Ceccarelli et al. 1996). As a result, dust and gas temperatures
can differ slightly, especially in the 100-200 K range
(e.g., Ceccarelli et al. 2000; Maret et al. 2002); however, at densities of 107 cm-3 or higher, the gas and dust in the warm inner region couple
efficiently. At low densities (<105 cm -3) and
temperatures (<50 K), any differences between gas and dust
temperature depend on the source parameters (e.g., luminosity,
total envelope mass) and the external interstellar radiation field
(ISRF). Doty & Neufeld (1997) show in their Fig. 12 that these
differences are generally small, about 10 K or less for low-mass
YSOs, and typically only exist at radii greater than 2000 AU.
Boonman et al. (2003) show that for high-mass YSOs, the water line
emission for a full radiative transfer calculation of the gas
temperature differs negligible from that calculated using the
![]() assumption.
assumption.
Our choice of
![]() assumes that water
vapor at larger radii does not contribute to the total water
line emission due to the low densities (<105 cm-3) and
temperatures (<15 K) in these regions. This assumption
mostly affects the transitions leading to the ground states. Any
such material is able to absorb water emission for optically thick
lines, and lead to weak emission lines in observations taken with a
beam that is much larger than our adopted source sizes. However,
such extended envelope material is almost indistinguishable from any
larger scale cloud complexes not directly related to the source.
Such contributions from large-scale clouds need to be taken into
account on a source-by-source basis, but are beyond the scope of
this work. The protostellar envelopes are assumed to be shielded
from strong external radiation fields by surrounding molecular cloud
material. If directly exposed to outside radiation, the temperature in
the outer envelopes is affected by the ISRF, but material is not
heated by more than 40 K for the ISRF found within the Orion
starforming region (Jørgensen et al. 2006). Low-mass starforming regions
are expected to have significantly lower ISRF. External radiation is
not considered for these models.
assumes that water
vapor at larger radii does not contribute to the total water
line emission due to the low densities (<105 cm-3) and
temperatures (<15 K) in these regions. This assumption
mostly affects the transitions leading to the ground states. Any
such material is able to absorb water emission for optically thick
lines, and lead to weak emission lines in observations taken with a
beam that is much larger than our adopted source sizes. However,
such extended envelope material is almost indistinguishable from any
larger scale cloud complexes not directly related to the source.
Such contributions from large-scale clouds need to be taken into
account on a source-by-source basis, but are beyond the scope of
this work. The protostellar envelopes are assumed to be shielded
from strong external radiation fields by surrounding molecular cloud
material. If directly exposed to outside radiation, the temperature in
the outer envelopes is affected by the ISRF, but material is not
heated by more than 40 K for the ISRF found within the Orion
starforming region (Jørgensen et al. 2006). Low-mass starforming regions
are expected to have significantly lower ISRF. External radiation is
not considered for these models.
To limit the model complexity, the wide range of parameters was
reduced to four variables (see Table 1). The
density at 1000 AU,
![]() )
and the exponent of the density
power law p are two of these. Jørgensen et al. (2002) observed many
low-mass YSOs and inferred densities at 1000 AU between
)
and the exponent of the density
power law p are two of these. Jørgensen et al. (2002) observed many
low-mass YSOs and inferred densities at 1000 AU between
![]() to
to
![]() cm-3. Accordingly, three values,
cm-3. Accordingly, three values,
![]() ,
and
,
and
![]() cm-3 were chosen
to sample this range, and p was chosen to be either 1.5 or 2.0.
The stellar variables are reduced to a single variable, the
luminosity. Models using luminosities of 2, 7, and 25
cm-3 were chosen
to sample this range, and p was chosen to be either 1.5 or 2.0.
The stellar variables are reduced to a single variable, the
luminosity. Models using luminosities of 2, 7, and 25 ![]() are explored to represent the wide range of luminosities observed in
low-mass protostars. Although the surface temperature of the protostar
cannot be derived directly, it is assumed to be around 5000 K for
low-mass young stars, regardless of the luminosity or age. Test models
show that, due to the reprocessing of stellar photons into IR/thermal
photons very close to the star, the stellar effective temperature has
little influence on the modeling. The final variable is the
gas-phase water abundance, to be discussed below. Table 1 summarizes all the adopted parameters. The
resulting masses and inner and outer radii for each envelope model can
be found in Table 2.
are explored to represent the wide range of luminosities observed in
low-mass protostars. Although the surface temperature of the protostar
cannot be derived directly, it is assumed to be around 5000 K for
low-mass young stars, regardless of the luminosity or age. Test models
show that, due to the reprocessing of stellar photons into IR/thermal
photons very close to the star, the stellar effective temperature has
little influence on the modeling. The final variable is the
gas-phase water abundance, to be discussed below. Table 1 summarizes all the adopted parameters. The
resulting masses and inner and outer radii for each envelope model can
be found in Table 2.
Because of the gradient in temperature, the water abundance X with
respect to H2 is expected to vary within YSO envelopes. Previous
studies of low- and high-mass YSOs used a variety of H2O
observations with ISO-LWS, ISO-SWS, and/or SWAS to constrain the water
abundance profile in protostellar envelopes to have a ``jump'' in
abundance at a characteristic temperature around 100 K
(e.g., van der Tak et al. 2006; Maret et al. 2002; Boonman et al. 2003). Such ``jumps'' have also
been confirmed by ground-based observations of other molecules such as
CH3OH and H2CO
(e.g., Ceccarelli et al. 2000; van der Tak et al. 2000; Maret et al. 2004; Schöier et al. 2002; Jørgensen 2004).
The abundance of water in the inner region X0 is high for two
reasons. First, most water exists in the gas phase
above 100 K, the temperature at which water ice evaporates from the
grains. Second, gas-phase reactions of atomic oxygen with molecular
hydrogen drive all oxygen into water at high temperatures (T>230 K) (Charnley et al. 2001).
However, in regions where the temperature drops below 100 K, water is mostly frozen out onto the
grains, and only trace amounts of gaseous water are present
with an abundance
![]() .
.
Accordingly, ``jump'' abundances are assumed for all models with X0,
the abundance of the warm inner region, taken to be 10-4 or
10-6 , and
![]() ,
the abundance in the cold outer region,
taken to be 10-6, 10-7, or 10-8. These values cover the
range of inferred abundances from observations to date for embedded
protostars. Although beam-averaged H2O abundances below
10-8 have been observed for B 68 and Oph-D (Bergin & Snell 2002),
such clouds are starless. At the extremely low temperatures of <15 K, virtually all heavy elements are frozen out. Abundances as low as
10-11 were tested by Boonman et al. (2003), but models with outer
abundances of 10-8 were preferred in fitting the combined SWAS
and ISO-LWS data. One combination of abundances is a
constant abundance at 10-6, included to investigate the
differences between ``jump'' and constant abundance profiles. A finer
grid of abundances within this range is explored for the L 483 model.
Figure 1 includes the assumed abundance structure.
Our models do not consider a so-called ``drop'' abundance profile
(see Schöier et al. 2004), in which the abundance in the outermost
part is higher due to longer timescales for freeze-out at lower
densities and due to photodesorption of ices (Bergin & Melnick 2005). Such an
abundance profile would result in more self-absorption in the
ground-state lines, equivalent to absorption caused by the cold
fore-ground material not associated with the protostellar system.
,
the abundance in the cold outer region,
taken to be 10-6, 10-7, or 10-8. These values cover the
range of inferred abundances from observations to date for embedded
protostars. Although beam-averaged H2O abundances below
10-8 have been observed for B 68 and Oph-D (Bergin & Snell 2002),
such clouds are starless. At the extremely low temperatures of <15 K, virtually all heavy elements are frozen out. Abundances as low as
10-11 were tested by Boonman et al. (2003), but models with outer
abundances of 10-8 were preferred in fitting the combined SWAS
and ISO-LWS data. One combination of abundances is a
constant abundance at 10-6, included to investigate the
differences between ``jump'' and constant abundance profiles. A finer
grid of abundances within this range is explored for the L 483 model.
Figure 1 includes the assumed abundance structure.
Our models do not consider a so-called ``drop'' abundance profile
(see Schöier et al. 2004), in which the abundance in the outermost
part is higher due to longer timescales for freeze-out at lower
densities and due to photodesorption of ices (Bergin & Melnick 2005). Such an
abundance profile would result in more self-absorption in the
ground-state lines, equivalent to absorption caused by the cold
fore-ground material not associated with the protostellar system.
The effects of micro-turbulence within the envelope are
represented by a velocity dispersion
![]() ,
,
![]() km s-1(b=1 km s-1, with b the Doppler parameter),
consistent with the typical line widths observed for optically thin
rotational emission in low-mass YSO envelopes
(Jørgensen et al. 2005,2004,2002). For a more thorough
discussion of the effects of the choice of this value,
see Sect. 5.2. An infall velocity profile was included, based on the
velocity profiles for collapsing clouds as found by Shu (1977). This velocity profile was scaled to a velocity of 4 km s-1 at the inner radius
km s-1(b=1 km s-1, with b the Doppler parameter),
consistent with the typical line widths observed for optically thin
rotational emission in low-mass YSO envelopes
(Jørgensen et al. 2005,2004,2002). For a more thorough
discussion of the effects of the choice of this value,
see Sect. 5.2. An infall velocity profile was included, based on the
velocity profiles for collapsing clouds as found by Shu (1977). This velocity profile was scaled to a velocity of 4 km s-1 at the inner radius
![]() .
At radii of a few hundred AU, the micro-turbulent velocity
dominates over the infall velocity, which is the scale probed mostly by
single-dish observations (e.g., Jørgensen et al. 2004). H2 is
assumed to be in a 1:1 ortho to para ratio. Water itself is in 3:1
ortho to para ratio. Collisional rate coefficients for both ortho-
and para-H2O with ortho- and para-H2 were obtained from the
LAMDA database (Schöier et al. 2005) based on calculations by Green et al. (1993) for temperatures in the range from 20 to 2000 K. New rate coefficients have recently been published
(Faure et al. 2007; Dubernet & Grosjean 2002; Phillips et al. 1996; Grosjean et al. 2003)
.
At radii of a few hundred AU, the micro-turbulent velocity
dominates over the infall velocity, which is the scale probed mostly by
single-dish observations (e.g., Jørgensen et al. 2004). H2 is
assumed to be in a 1:1 ortho to para ratio. Water itself is in 3:1
ortho to para ratio. Collisional rate coefficients for both ortho-
and para-H2O with ortho- and para-H2 were obtained from the
LAMDA database (Schöier et al. 2005) based on calculations by Green et al. (1993) for temperatures in the range from 20 to 2000 K. New rate coefficients have recently been published
(Faure et al. 2007; Dubernet & Grosjean 2002; Phillips et al. 1996; Grosjean et al. 2003)![]() . For a general discussion of uncertainties in molecular data, see Schöier et al. (2005).
. For a general discussion of uncertainties in molecular data, see Schöier et al. (2005).
The excitation and radiative transfer of the rotational water lines were calculated using the spherically symmetric version of the RATRAN code (Hogerheijde & van der Tak 2000). First, level populations were computed for all H2O levels with energies up to 2000 K for the model envelope using full Monte Carlo radiative transfer. Individual iterations use a convergence criterion of 10-6 on the relative error of the fractional population for the solution of the statistical equilibrium. Iterations continue with increasing amounts of photons, until the greatest relative difference between fractional populations over all cells and all levels of three subsequent iterations is less than 1/6. In practice this means that the vast majority of cells and levels are converged to much smaller relative errors. Far-infrared radiation from the dust and CMB are included in the H2O excitation and line formation. This inclusion makes it possible to investigate infrared pumping, self-absorption of a line, and absorption against the dust continuum. Even though many levels are very sparsely populated, tests show that it is necessary to include the higher levels to obtain an accurate population distribution throughout the model.
The populations are then used to reconstruct detailed line profiles
through ray-tracing, which can be convolved with any beam or area. It
can also be used to make velocity maps of the source. The adopted spectral
resolution is 0.05 km s-1. RATRAN was benchmarked
against many codes (van Zadelhoff et al. 2002). Furthermore, it was
part of a recent benchmark test![]() for line modeling of
H2O (van der Tak et al. 2005).
for line modeling of
H2O (van der Tak et al. 2005).
Table 3: Key water lines observable with Herschel HIFI and PACS.
Although level populations were calculated for all levels up to
![]() K, only lines with an upper energy level below 500 K were selected for the presentation of results (see Table 3). Both H2O and H218O were modeled with a focus on lines that fall into the Herschel wavelength range. The
16O:18O isotope ratio was assumed to be 550:1, the ratio in
the local ISM (Wilson & Rood 1994).
All generic models are placed at 150 pc, the typical distance of most
nearby low-mass starforming regions such as Ophiuchus, Taurus, and
Chameleon. Results were convolved with the appropriate Herschel beams
and given in main beam temperatures. For reference, the typical
sensitivities expected with HIFI (5
K, only lines with an upper energy level below 500 K were selected for the presentation of results (see Table 3). Both H2O and H218O were modeled with a focus on lines that fall into the Herschel wavelength range. The
16O:18O isotope ratio was assumed to be 550:1, the ratio in
the local ISM (Wilson & Rood 1994).
All generic models are placed at 150 pc, the typical distance of most
nearby low-mass starforming regions such as Ophiuchus, Taurus, and
Chameleon. Results were convolved with the appropriate Herschel beams
and given in main beam temperatures. For reference, the typical
sensitivities expected with HIFI (5![]() ,
0.5 h, 0.5 km s-1 resolution)
are 60 mK for 557 GHz, 180 mK at 1130 GHz, and 600 mK at 1669 GHz. For
PACS, limiting line fluxes (5
,
0.5 h, 0.5 km s-1 resolution)
are 60 mK for 557 GHz, 180 mK at 1130 GHz, and 600 mK at 1669 GHz. For
PACS, limiting line fluxes (5![]() ,
0.5 h, point source) range
from
,
0.5 h, point source) range
from
![]() W m-2 to
W m-2 to
![]() W m-2
W m-2![]() . To convert from main beam temperatures
. To convert from main beam temperatures
![]() to fluxes
to fluxes ![]() in Jy (10-26 W m-2 Hz-1), use the formula
in Jy (10-26 W m-2 Hz-1), use the formula
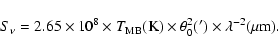 |
(2) |
As an illustrative model, the isolated Class 0 source L 483,
(Motte & André 2001)
located at 200 pc, was modeled to investigate the sensitivity of the
water line intensities to different abundances. This source has been
studied extensively by Jørgensen et al. (2002) and Jørgensen (2004) and
its physical and chemical structure is well-constrained through
continuum and line data from (sub)millimeter single-dish telescopes
and interferometers. The well-determined envelope and source
parameters (
![]() and
and
![]() cm-3) are roughly in the middle of
our parameter range, making L 483 an excellent test-case for modeling water
emission. Only the inferred density slope, p=0.9, is somewhat
flatter than for other sources, but this does not influence the
model trends. For CO, a jump abundance at an evaporation temperature
of
cm-3) are roughly in the middle of
our parameter range, making L 483 an excellent test-case for modeling water
emission. Only the inferred density slope, p=0.9, is somewhat
flatter than for other sources, but this does not influence the
model trends. For CO, a jump abundance at an evaporation temperature
of
![]() K was found to explain the observed molecular
lines. Any compact disk is constrained to a mass of 0.012
K was found to explain the observed molecular
lines. Any compact disk is constrained to a mass of 0.012 ![]() using interferometer observations with the Sub-Millimeter Array (Jørgensen et al. 2007), negligible
compared to the total estimated envelope mass of 4.4
using interferometer observations with the Sub-Millimeter Array (Jørgensen et al. 2007), negligible
compared to the total estimated envelope mass of 4.4 ![]() out to the 10 K radius of 10 000 AU. In addition, this source has been observed with ISO-LWS
(Giannini et al. 2001). The best-fit parameters from the dust radiative
transfer (Y=1400, p=0.9,
out to the 10 K radius of 10 000 AU. In addition, this source has been observed with ISO-LWS
(Giannini et al. 2001). The best-fit parameters from the dust radiative
transfer (Y=1400, p=0.9,
![]() ), which fit both
the SED and the spatial extent of the SCUBA continuum data,
determine the physical structure of the envelope.
), which fit both
the SED and the spatial extent of the SCUBA continuum data,
determine the physical structure of the envelope.
![]() (at
T=250 K) is 9.9 AU for this rather shallow density profile,
and
(at
T=250 K) is 9.9 AU for this rather shallow density profile,
and
![]() is
is ![]() 10 000 AU. The radius where water freezes
out onto the grains (T=100 K) is located at 35 AU. This L 483 model
was used to explore a wider variety of water abundances than the
generic models. Specifically, values of
10 000 AU. The radius where water freezes
out onto the grains (T=100 K) is located at 35 AU. This L 483 model
was used to explore a wider variety of water abundances than the
generic models. Specifically, values of
![]() ,
and
,
and
![]() were used for X0 and
were used for X0 and
![]() ,
and
,
and
![]() for
for ![]() .
All
other parameters were kept fixed. Ortho- and para-water were modeled
separately, and water abundances are given for ortho- or para-water
individually instead of the combined total water abundance with the used 3:1 ortho to para ratio. This allows independent probes of the ortho to para ratio. Thus, X0 and
.
All
other parameters were kept fixed. Ortho- and para-water were modeled
separately, and water abundances are given for ortho- or para-water
individually instead of the combined total water abundance with the used 3:1 ortho to para ratio. This allows independent probes of the ortho to para ratio. Thus, X0 and ![]() refer to either ortho- or para-H2O, depending on the line in question.
refer to either ortho- or para-H2O, depending on the line in question.
Table 4:
Integrated intensities,
![]() [K km s-1], for H2O and H218O lines for L 483 models with various abundances. Negative values indicate strong (self-) absorbed lines.
[K km s-1], for H2O and H218O lines for L 483 models with various abundances. Negative values indicate strong (self-) absorbed lines.
In Table 4 the integrated emission of both H216O
and H218O lines, observable with Herschel-HIFI (see Table 3), are presented for the reference grid of L 483, whereas Table 5 presents the peak
temperatures. Detailed contour plots of all HIFI lines as functions of
X0 and ![]() are presented in Fig. 2 the online appendix. Many of the trends discussed below are similar to those found for AFGL 2591, as discussed in Poelman & van der Tak (2007).
Overall, lines are found to belong to three categories. First, all
excited H218O and several H2O highly excited
(
are presented in Fig. 2 the online appendix. Many of the trends discussed below are similar to those found for AFGL 2591, as discussed in Poelman & van der Tak (2007).
Overall, lines are found to belong to three categories. First, all
excited H218O and several H2O highly excited
(
![]() K) lines are completely optically thin. They have
Gaussian profiles with widths that depend on the turbulent width. Due to
the freeze-out of water onto grains below 100 K, these optically thin
lines probe the inner warm dense region. For the model where water has
a constant abundance of 10-6, emission from the warm dense inner
region still dominates and is optically thin (either due to the low
population of the highly excited states or the low abundance of
H218O). A good example is the H2O 524-431 970 GHz
line shown in Fig. 2 (right).
K) lines are completely optically thin. They have
Gaussian profiles with widths that depend on the turbulent width. Due to
the freeze-out of water onto grains below 100 K, these optically thin
lines probe the inner warm dense region. For the model where water has
a constant abundance of 10-6, emission from the warm dense inner
region still dominates and is optically thin (either due to the low
population of the highly excited states or the low abundance of
H218O). A good example is the H2O 524-431 970 GHz
line shown in Fig. 2 (right).
Table 5: Peak temperatures [K] of H2O lines for L 483 models of various abundances. Negative values primarily indicate absorption into the dust continuum.
The ground state lines of both H218O and H2O, together with
most H2O excited lines with energies below 200 K, provide a strong
contrast with the optically thin lines. These lines only probe the
outer region. Even an abundance of water as low as 10-8 in the
cold outer envelope produces a high enough column for these lines to
become optically thick. The extremely high optical depth (![]() )
and the absorptions into the dust further prevent the integrated
intensity from probing the entire envelope. Thus, these lines trace
the outer abundance
)
and the absorptions into the dust further prevent the integrated
intensity from probing the entire envelope. Thus, these lines trace
the outer abundance
![]() ,
and self-absorption and absorption
of the dust continuum are commonly found in their line profiles.
However, most optically thick lines have wings that are
either optically thin or less optically thick.
These wings may be able to probe the inner region up to the
boundary layer around T=100 K. See the 110-101 line in Fig. 2
(left), Table 5 and the spectra in
Figs. 3 and 4
(discussed in Sect. 3.4).
,
and self-absorption and absorption
of the dust continuum are commonly found in their line profiles.
However, most optically thick lines have wings that are
either optically thin or less optically thick.
These wings may be able to probe the inner region up to the
boundary layer around T=100 K. See the 110-101 line in Fig. 2
(left), Table 5 and the spectra in
Figs. 3 and 4
(discussed in Sect. 3.4).
| |
Figure 3:
H2O spectra for an abundance X0 of 10-5 for the 110-101 (557 GHz, left), 212-101 (1669 GHz middle), and 312-303 (1097 GHz right) lines. Lines are shown for
|
| Open with DEXTER | |
| |
Figure 4:
H2O spectra for an abundance
|
| Open with DEXTER | |
Finally, some lines are optically thick for a high X0-
![]() combination, but are optically thin at low abundances. It is not known
a-priori if these lines originate within the cold outer envelope or
the warm dense inner regions. Examples are several of the highly
excited H2O lines, but such dependencies are also seen for lowly
excited H218O lines. Figure 2 (middle) shows an example with the p-H218O 202-111 line. It can be seen that, depending on the total column of water, this line either traces
combination, but are optically thin at low abundances. It is not known
a-priori if these lines originate within the cold outer envelope or
the warm dense inner regions. Examples are several of the highly
excited H2O lines, but such dependencies are also seen for lowly
excited H218O lines. Figure 2 (middle) shows an example with the p-H218O 202-111 line. It can be seen that, depending on the total column of water, this line either traces
![]() at high
columns or X0 at lower columns. For the H218O lines, a clear
dividing line between dependency on X0 or
at high
columns or X0 at lower columns. For the H218O lines, a clear
dividing line between dependency on X0 or ![]() lies at
lies at
![]() (see online appendix). Such a division is less clear for H216O. The dust
can become optically thick, especially at high frequencies, so the
higher frequency lines will not be able to probe the inner region at
all. For the L 483 models, this only takes place at
frequencies higher than 1500 GHz, but see Sect. 5 for further
discussion. In the following, individual H2O and H218O lines
are discussed in more detail.
(see online appendix). Such a division is less clear for H216O. The dust
can become optically thick, especially at high frequencies, so the
higher frequency lines will not be able to probe the inner region at
all. For the L 483 models, this only takes place at
frequencies higher than 1500 GHz, but see Sect. 5 for further
discussion. In the following, individual H2O and H218O lines
are discussed in more detail.
The main isotopologue of water, H216O, is optically thick in
most transitions considered here.
All lines with
![]() and 2 are optically thick and trace
the outer cold envelope. Most other lines trace either the warm inner
or cold outer envelope. The integrated intensities of these ``hybrid''
lines depend sensitively on the precise abundance parameters of the L 483 reference model. In particular, the radius where the line turns
optically thick is comparable to that where the one where the temperature reaches
100 K for this model. These are the 221-212, 312-221,
312-303, 321-312 and 422-413 lines. At low
abundances of
and 2 are optically thick and trace
the outer cold envelope. Most other lines trace either the warm inner
or cold outer envelope. The integrated intensities of these ``hybrid''
lines depend sensitively on the precise abundance parameters of the L 483 reference model. In particular, the radius where the line turns
optically thick is comparable to that where the one where the temperature reaches
100 K for this model. These are the 221-212, 312-221,
312-303, 321-312 and 422-413 lines. At low
abundances of
![]() ,
they depend more on X0. If the
abundance in the outer region is larger than
,
they depend more on X0. If the
abundance in the outer region is larger than
![]() ,
they
depend on
,
they
depend on
![]() instead. The integrated intensities range from
several hundreds of mK km s-1 in absorption to a few K km s-1 in emission, with peak brightness from 100 mK to 1 K, readily detectable with HIFI. The group of highly excited para-lines have peaks up to a few tens of mK, requiring much longer integration times.
instead. The integrated intensities range from
several hundreds of mK km s-1 in absorption to a few K km s-1 in emission, with peak brightness from 100 mK to 1 K, readily detectable with HIFI. The group of highly excited para-lines have peaks up to a few tens of mK, requiring much longer integration times.
Dependencies of the line strengths on abundances are not linear. An exception is whenever the line is completely optically thin over the entire profile. This is not the case for most lines and parts of the line profile will be optically thin and parts optically thick, causing complicated dependencies. For instance, the total integrated intensity of the 557 GHz line depends sensitively on the inner and outer abundances. Abundance combinations of 10-4/10-6 produce lines with less total emission than 10-6/10-6. The 10-6/10-6 combination contains less water emission originating from the warm inner regions, but more dust continuum is able to escape the inner regions in the 10-6/10-6. This influences the population distribution in the outer region, resulting in less central absorption. Since absorption is a major feature within this line profile, the total integrated line intensity effectively goes up.
Because of the low abundance of the H218O isotopologue, most of
its lines are optically thin. Only the three transitions connecting to
the ground levels of ortho- and para-H218O - 111-000,
110-101, and 212-101 - have optical depths higher than 5 for all abundances. However, excited lines with
![]() are
optically thick in their line centers for
X0>10-5.
The integrated intensities of these H218O lines range from a few
hundred mK km s-1 in absorption to a few tens of mK km s-1 in
emission, whereas peak temperatures range from a few mK to a few tens
of mK, thus requiring long integration times. Due to the low
abundance, the dependence on either X0 or
are
optically thick in their line centers for
X0>10-5.
The integrated intensities of these H218O lines range from a few
hundred mK km s-1 in absorption to a few tens of mK km s-1 in
emission, whereas peak temperatures range from a few mK to a few tens
of mK, thus requiring long integration times. Due to the low
abundance, the dependence on either X0 or
![]() is much more
evident than for H216O (see Fig. 2 for
example). The optically thick ground-state lines accurately trace
is much more
evident than for H216O (see Fig. 2 for
example). The optically thick ground-state lines accurately trace
![]() ,
while optically thin excited lines only depend on
X0. The few optically thick excited lines trace X0 as well,
since the
,
while optically thin excited lines only depend on
X0. The few optically thick excited lines trace X0 as well,
since the ![]() surface lies within the 100 K radius.
Higher excitation H218O lines are not very strong, in the range
of a few micro-K to a few milli-K, too weak to be detectable with HIFI
in reasonable integration times.
surface lies within the 100 K radius.
Higher excitation H218O lines are not very strong, in the range
of a few micro-K to a few milli-K, too weak to be detectable with HIFI
in reasonable integration times.
A number of characteristic line profiles are presented in Figs. 3 and 4. The continuum has been subtracted so that the profiles can be readily compared on the same scale. The total profile contains valuable information about the envelope structure and velocity profile, none of which can be determined using the integrated line intensity alone. As seen in the examples, there is a wide variety of model profiles depending on a number of parameters. First, the excitation energy of the upper state, the total water column density and the critical density of the line in question will determine whether an emission line is optically thick, thin or a combination of both. Most lines show a combination, with optically thin wings around an optically thick line center. Second, the width depends on the systematic and turbulent velocity. Third, water in the colder outer envelope will absorb photons and scatter the radiation, causing an absorption feature. Finally, the optical depth of dust itself blocks line emission at frequencies above 1500 GHz originating in the inner region. In the following these profile shapes are discussed in more detail.
The profiles of optically thin lines are Gaussian and are good tracers
of the velocity profile.
Optically thin lines always trace the inner
warm region, where the higher excitation states are populated. The
ratio of the line wing over the peak temperature can vary, depending
on the excitation energy of the line. Higher excitation lines are
broader, while low excitation lines have a narrower peak with very
weak line wings. An example in Fig. 4 is the
312-303 1097 GHz line, which is completely optically thin
for
![]() .
The line center becomes optically thick at
.
The line center becomes optically thick at
![]() and thus decreases, but the optically thin line
wings are noticeably higher in emission. At
and thus decreases, but the optically thin line
wings are noticeably higher in emission. At
![]() ,
the
optically thick line center is brighter than at 10-5 due to the
high abundance, but still weaker than the optically thin emission at
,
the
optically thick line center is brighter than at 10-5 due to the
high abundance, but still weaker than the optically thin emission at
![]() .
.
The profiles of optically thick lines are much more complicated. Their wings can either be optically thick or thin, depending on the abundances and frequency of the line. This gives rise to three different profiles.
(i) Absorption depth: if dust is optically thick (e.g., at 1669 GHz),
the depth is independent of both X0 and
![]() as long as
as long as
![]() ,
and only depends on the radius where the dust turns
optically thick, setting the continuum level. In Figs. 3 and 4 (middle) the 1669 GHz continuum-subtracted line is always at -0.2 K. If dust is optically thin (e.g., the 557 GHz 110-101 line), the depth v of the absorption depends on both
,
and only depends on the radius where the dust turns
optically thick, setting the continuum level. In Figs. 3 and 4 (middle) the 1669 GHz continuum-subtracted line is always at -0.2 K. If dust is optically thin (e.g., the 557 GHz 110-101 line), the depth v of the absorption depends on both ![]() and X0 and is caused by
self-absorption of the water in the cold outer region against the warm
emission. Indeed, it is found that water at around 70-90 K acts as a
warm background emitter and water at 20 K as the cold absorber.
and X0 and is caused by
self-absorption of the water in the cold outer region against the warm
emission. Indeed, it is found that water at around 70-90 K acts as a
warm background emitter and water at 20 K as the cold absorber.
(ii) Absorption width: again there is a difference between high and
low optical depths of dust. For 1669 GHz the width of the absorption
depends on
![]() ,
but not on X0. For 557 GHz, there is no
dependence on abundance. The width of the absorption is the same for
varying X0 (the temperature at which the water emits changes
little), and even though the profiles appear different for different
,
but not on X0. For 557 GHz, there is no
dependence on abundance. The width of the absorption is the same for
varying X0 (the temperature at which the water emits changes
little), and even though the profiles appear different for different
![]() ,
this can be attributed to the changing absorption depth,
not width.
,
this can be attributed to the changing absorption depth,
not width.
(iii) Line wing strength: the strength of the line wing, which often
contains the bulk of the line emission, is determined by the optical
depth of the dust and gas. Most often, the peaks seen in the
wings of the ground-state lines are still optically thick. The wings
trace both
![]() (see 110-101 and 212-101lines in Fig. 3, left, middle), which still
contain large columns of the gas, and X0 (110-101and 212-101 Fig. 4, left, middle),
although in that case the relation is not straightforward.
Line pumping from the warm gas further inwards is the main origin of
the dependency from
X0=10-4 to 10-5. However, if
(see 110-101 and 212-101lines in Fig. 3, left, middle), which still
contain large columns of the gas, and X0 (110-101and 212-101 Fig. 4, left, middle),
although in that case the relation is not straightforward.
Line pumping from the warm gas further inwards is the main origin of
the dependency from
X0=10-4 to 10-5. However, if
![]() and X0 are low enough, the line wings turn optically
thin and are significantly enhanced (Fig. 3) because higher temperatures are probed. This behavior is seen for a
and X0 are low enough, the line wings turn optically
thin and are significantly enhanced (Fig. 3) because higher temperatures are probed. This behavior is seen for a ![]() /X0 combination of 10-7/10-6where the line wings are brighter than for
/X0 combination of 10-7/10-6where the line wings are brighter than for ![]() /X0 combinations of 10-7/10-4 and 10-7/10-5.
/X0 combinations of 10-7/10-4 and 10-7/10-5.
Although the beams for HIFI and the accompanying dilution
factors are large compared to the physical size of the warm gas (see
Table 3), the inner warm region is detectable
through the higher excited states. The outer cold envelope is
completely transparent for these lines. Considering the expected
sensitivities of HIFI, a combination of different lines can constrain
the water abundance profile. The H218O 202-111 994 GHz
line in HIFI Band 4 is mostly optically thin and traces X0, except
at H216O
![]() abundances higher than
5
abundances higher than
5
![]() .
However, the line is weak (a few tens of mK) and
needs at least a few hours of integration to be detected. A possible
alternative is the high excitation H216O 312-303 line
in HIFI Band 4, which can be detected in roughly an hour of
integration. It traces X0 at high X0 abundances, but for X0lower than 10-5, emission coming from the colder outer part
dominates, thus tracing
.
However, the line is weak (a few tens of mK) and
needs at least a few hours of integration to be detected. A possible
alternative is the high excitation H216O 312-303 line
in HIFI Band 4, which can be detected in roughly an hour of
integration. It traces X0 at high X0 abundances, but for X0lower than 10-5, emission coming from the colder outer part
dominates, thus tracing
![]() .
This emission originates in the
region with temperatures ranging from 70-100 K. Once the inner
abundance X0 is well-constrained, ground-state lines can in turn be
used to constrain the abundance in the outer region. The bright wings
of the 557 GHz line (HIFI Band 1) are detectable within a few minutes,
but the entire line profile is needed for proper analysis (see Sect. 3.4). The dependence on
.
This emission originates in the
region with temperatures ranging from 70-100 K. Once the inner
abundance X0 is well-constrained, ground-state lines can in turn be
used to constrain the abundance in the outer region. The bright wings
of the 557 GHz line (HIFI Band 1) are detectable within a few minutes,
but the entire line profile is needed for proper analysis (see Sect. 3.4). The dependence on
![]() can be traced most accurately
using the line profiles of the 111-000 1113 GHz para-H2O
and 1101 GHz para-H218O lines in Band 4, but resolving these
profiles requires much longer integration times than the 557 GHz line.
The 1667 GHz 212-101 ortho-H2O line in Band 6 is intrinsically
brighter, but will take almost an hour of integration due to the low
sensitivity of HIFI at this frequency. In addition, dust can become
optically thick at this high frequency so that the line profile only
traces the structure in the outer envelope.
can be traced most accurately
using the line profiles of the 111-000 1113 GHz para-H2O
and 1101 GHz para-H218O lines in Band 4, but resolving these
profiles requires much longer integration times than the 557 GHz line.
The 1667 GHz 212-101 ortho-H2O line in Band 6 is intrinsically
brighter, but will take almost an hour of integration due to the low
sensitivity of HIFI at this frequency. In addition, dust can become
optically thick at this high frequency so that the line profile only
traces the structure in the outer envelope.
The optically thick H216O 202-111 988 GHz line, with its optically thin H218O counterpart are the best candidates for determining the optical depth of water, but the H218O lines require significant integration time (see above). An alternative is provided by comparison between of the 548 GHz H218O and 557 GHz H216O ground-state lines, but H218O is still optically thick so that detailed modeling is required. The 111-0001113 GHz, 202-111 988 GHz, and 211-202 752 GHz para-H2O lines are well-suited to probing the physical structure of the envelope. Due to their different excitation energies and optical depths, these lines probe different environments within the protostellar envelope, and their line ratios are not affect by the uncertain ortho/para ratio.
The source L 483 was observed with ISO-LWS (Giannini et al. 2001). The para
220-111 line at 2968 GHz (101 ![]() m) was detected with a
flux of
m) was detected with a
flux of
![]() W cm-2 and the ortho
212-101 line at 1670 GHz (179.5
W cm-2 and the ortho
212-101 line at 1670 GHz (179.5 ![]() m) was found to have an
upper limit of
m) was found to have an
upper limit of
![]() W cm-2. The low LWS
resolving power of
W cm-2. The low LWS
resolving power of
![]() (
(![]() 1500 km s-1) was insufficient for determining the effect of any
self-absorption or disentangling outflow components from quiescent
envelope material. The best-fitting LVG model for the high-J CO
lines gave a component of gas with T=850-1800 K; it is expected
that this hot gas contributes significantly to the water emission (Giannini et al. 2001).
1500 km s-1) was insufficient for determining the effect of any
self-absorption or disentangling outflow components from quiescent
envelope material. The best-fitting LVG model for the high-J CO
lines gave a component of gas with T=850-1800 K; it is expected
that this hot gas contributes significantly to the water emission (Giannini et al. 2001).
The above models, corrected for the ISO beam of 80'', are compared to the observed intensity. Our models show a strong absorption into the dust for both lines with optically thin line wings. Integrated intensities range from -
![]() up to
up to
![]() W cm-2 for the 220-111 line and from
W cm-2 for the 220-111 line and from
![]() W cm-2 to
W cm-2 to
![]() W cm-2for the ortho 212-101 line for different X0-
W cm-2for the ortho 212-101 line for different X0-
![]() combinations. The best fit, using both the detection and upper limit,
is found for an outer abundance of 10-7 and an inner abundance
between 10-6 and 10-5. The detected line is reproduced
within 30%, while the upper limit is only 50% higher than the
intensity produced by the model. For lower values of
combinations. The best fit, using both the detection and upper limit,
is found for an outer abundance of 10-7 and an inner abundance
between 10-6 and 10-5. The detected line is reproduced
within 30%, while the upper limit is only 50% higher than the
intensity produced by the model. For lower values of ![]() ,
around 10-8, the integrated emission in our model is almost an
order of magnitude lower than the observed 220-111line. Such low outer abundances are found for cold regions in the
envelopes around high-mass YSOs (Boonman et al. 2003), but appear
inconsistent with the data for this low-mass YSO, unless the detected
emission originates fully in the outflow. Higher inner abundances
cannot be ruled out. However, the self-absorption in the models
becomes stronger, resulting in a worse fit to the detected line and
upper limit.
,
around 10-8, the integrated emission in our model is almost an
order of magnitude lower than the observed 220-111line. Such low outer abundances are found for cold regions in the
envelopes around high-mass YSOs (Boonman et al. 2003), but appear
inconsistent with the data for this low-mass YSO, unless the detected
emission originates fully in the outflow. Higher inner abundances
cannot be ruled out. However, the self-absorption in the models
becomes stronger, resulting in a worse fit to the detected line and
upper limit.
Other water lines within the ISO-LWS domain were not detected. The
derived upper limits were found to be at least a factor 5 higher than
fluxes predicted from all possible models. At short (>80 ![]() m)
wavelengths, the difference is a few orders of magnitude. Since all
lines are unresolved, no conclusion can be reached as to whether the
detected water emission is dominated by outflow contributions or by
thermal excitation within the circumstellar envelope with a high
abundance. This example illustrates the need for spectrally and
spatially resolved data of a number of lines to disentangle the
different physical components.
m)
wavelengths, the difference is a few orders of magnitude. Since all
lines are unresolved, no conclusion can be reached as to whether the
detected water emission is dominated by outflow contributions or by
thermal excitation within the circumstellar envelope with a high
abundance. This example illustrates the need for spectrally and
spatially resolved data of a number of lines to disentangle the
different physical components.
Table 6:
Integrated intensities,
![]() [K km s-1], for H2O lines in the wide parameter grid for an abundance combination of
X0=10-4 and
[K km s-1], for H2O lines in the wide parameter grid for an abundance combination of
X0=10-4 and
![]() .
.
| |
Figure 5:
Examples of the luminosity dependence of line profiles for a
model with p=1.5,
X0=10-4,
|
| Open with DEXTER | |
| |
Figure 6:
Examples of the density dependence of line profiles for a
model with p=1.5,
X0=10-4,
|
| Open with DEXTER | |
Table 6 and Figs. 5 and 6 present the results for a grid probing the
parameters from Table 1 for a constant abundance
combination of 10-4 for X0 and 10-7 for
![]() .
Results for the full grid, including all probed
abundances, can be found in the online appendix. The main variables of
the grid - the luminosity, the density, and the density profile
steepness - are discussed within this section. The dependence on
abundance mirrors the behavior seen for the L 483 model discussed in
Sect. 3. For most combinations of envelope parameters, the H216O
transitions studied here are optically thick, sometimes with optically
thin line wings. For H218O lines, most transitions are
optically thin, although the three ground state lines are optically
thick at line center. The only optically thin H216O lines are
those for which the upper level of the transition has an excitation
temperature above 200-250 K, specifically the lines with J=3 and
higher. These lines are only optically thin if the densities are low
enough, <107 cm-3, and abundances are low,
X0<10-5 and
.
Results for the full grid, including all probed
abundances, can be found in the online appendix. The main variables of
the grid - the luminosity, the density, and the density profile
steepness - are discussed within this section. The dependence on
abundance mirrors the behavior seen for the L 483 model discussed in
Sect. 3. For most combinations of envelope parameters, the H216O
transitions studied here are optically thick, sometimes with optically
thin line wings. For H218O lines, most transitions are
optically thin, although the three ground state lines are optically
thick at line center. The only optically thin H216O lines are
those for which the upper level of the transition has an excitation
temperature above 200-250 K, specifically the lines with J=3 and
higher. These lines are only optically thin if the densities are low
enough, <107 cm-3, and abundances are low,
X0<10-5 and
![]() .
For typical low-mass envelopes, such densities are only encountered
within the inner region, where enhanced abundances are found.
Thus, because many higher excited H216O lines become optically
thick only in the very dense warm inner region, they are still good
tracers of the inner region (see Sect. 3.3.1 and
Fig. 4 right).
For high densities and thus higher envelope masses, the larger dust
column plays a major role by heavily influencing the water line
emission. This is discussed in Sect. 5.
.
For typical low-mass envelopes, such densities are only encountered
within the inner region, where enhanced abundances are found.
Thus, because many higher excited H216O lines become optically
thick only in the very dense warm inner region, they are still good
tracers of the inner region (see Sect. 3.3.1 and
Fig. 4 right).
For high densities and thus higher envelope masses, the larger dust
column plays a major role by heavily influencing the water line
emission. This is discussed in Sect. 5.
Figure 5 shows four lines for various luminosities. For
all lines, both the line strength and the absorption features
are stronger for higher luminosities. For optically thin lines, a
best fit can be found with a slope that has a power-law index of
![]() 0.8, i.e.
0.8, i.e.
![]() .
Figure 7 shows
two such power laws for the 220-211 1228 GHz line that
differentiate between the exact conditions and correspond to
0.45 L0.8 and
0.15 L0.8. The slope of the power law is determined
by the temperature profile, which determines the amount of warm gas
present in the dense inner region, and the filling factor of this warm
gas within the beam. This filling factor is not readily apparent,
since models have different values for
.
Figure 7 shows
two such power laws for the 220-211 1228 GHz line that
differentiate between the exact conditions and correspond to
0.45 L0.8 and
0.15 L0.8. The slope of the power law is determined
by the temperature profile, which determines the amount of warm gas
present in the dense inner region, and the filling factor of this warm
gas within the beam. This filling factor is not readily apparent,
since models have different values for
![]() and different
radii where T=100 K is reached depending on luminosity and density profile
(see Table 2).
The peak temperatures of these optically thin lines naturally follow a
similar dependence. Even for lines that display an optically thick
line center (e.g., the 331-404 line in
Fig. 5), the peak temperatures depend on luminosity in
a similar way to the completely optically thin lines.
and different
radii where T=100 K is reached depending on luminosity and density profile
(see Table 2).
The peak temperatures of these optically thin lines naturally follow a
similar dependence. Even for lines that display an optically thick
line center (e.g., the 331-404 line in
Fig. 5), the peak temperatures depend on luminosity in
a similar way to the completely optically thin lines.
For optically thick lines, a more complex dependency is seen in Fig. 5 (e.g., the 111-000 line). For such self-absorbed lines, the wings (which are optically thin) increase with L, while any absorption features also become more prominent. Although the peak temperatures do not follow the proposed power law of the optically thin lines, they will become easier to detect for more luminous sources.
![\begin{figure}
\par\includegraphics[width=7.2cm,clip]{images/lum.ps}\end{figure}](/articles/aa/full/2008/33/aa09426-08/Timg102.gif) |
Figure 7:
The modeled integrated intensity of the optically thin
220-211 1228 GHz line for
X0=10-4. Intensities are
shown for the 3 different values of
|
| Open with DEXTER | |
Figure 6 shows four lines for a range of densities, varying by more than an order of magnitude, corresponding to envelope masses ranging from 0.15 to 1.93
![]() .
The density at 1000 AU has a strong influence on the water line emission. For optically
thin lines, models with a constant p and constant luminosity show
that a power law with an index of 0.75 accurately describes the
dependence of line strengths on
.
The density at 1000 AU has a strong influence on the water line emission. For optically
thin lines, models with a constant p and constant luminosity show
that a power law with an index of 0.75 accurately describes the
dependence of line strengths on
![]() (see
Fig. 7). For optically thick lines, the line will
decrease in strength at higher densities, since the emission from the
warm inner part is veiled behind a larger, cold water column.
(see
Fig. 7). For optically thick lines, the line will
decrease in strength at higher densities, since the emission from the
warm inner part is veiled behind a larger, cold water column.
A higher density can also result in the dust becoming optically thick. This has an effect on the higher excited lines at high frequencies. For example, the optically thin 331-404 1893 GHz line (see Fig. 6, right) decreases by nearly two orders of magnitude in strength when the density increases from
![]() to
to
![]() cm-3. The dust is optically thin in the low-density models and optically thick at high density. Since the emission of this higher excitation line originates in the warm inner region, optically thick dust can obscure over 99% of the emission of this high frequency line (see Sect. 5).
cm-3. The dust is optically thin in the low-density models and optically thick at high density. Since the emission of this higher excitation line originates in the warm inner region, optically thick dust can obscure over 99% of the emission of this high frequency line (see Sect. 5).
The steepness of the power law used to define the density
distribution, p, also influences water line emission. Table 6 shows that lines differ subtly between p=2 and p=1.5. The line intensities of models with p= 2 are
lower by a factor ranging from 0.5 to 3 than those for models with
p= 1.5. Absorption features also differ in their depths for similar
models with only p varied. This is caused by differing temperature
profiles within the Herschel beams. Assuming equal
![]() at 1000 AU, the warm (T>100 K) region is significantly smaller for a
model with p=2 than for p=1.5. Although local densities are
higher by almost an order of magnitude, the beam dilution is too
severe to overcome such small regions.
at 1000 AU, the warm (T>100 K) region is significantly smaller for a
model with p=2 than for p=1.5. Although local densities are
higher by almost an order of magnitude, the beam dilution is too
severe to overcome such small regions.
The models were also calculated for the isotopologue
H218O. Similar to the L 483 models, transitions connected with
the ground state lines are optically thick for all models. H218O
excited lines with
![]() and 3 do have optically thick
centers for some combinations of abundance, luminosities and/or
densities, but are optically thin at densities below 106 cm-3. Higher excitation H218O lines are always optically thin. The best-fit power law slopes for the optically thin H218O
lines are the same as those for H216O. Of course, these
conclusions are limited by the optical depth of dust at the frequency
of the line, since H218O lines at high frequencies are affected
by dust. The precise frequency depends on the combination of
luminosity and the density profile (Sect. 5). Results for H218O can
be found in the online appendix.
and 3 do have optically thick
centers for some combinations of abundance, luminosities and/or
densities, but are optically thin at densities below 106 cm-3. Higher excitation H218O lines are always optically thin. The best-fit power law slopes for the optically thin H218O
lines are the same as those for H216O. Of course, these
conclusions are limited by the optical depth of dust at the frequency
of the line, since H218O lines at high frequencies are affected
by dust. The precise frequency depends on the combination of
luminosity and the density profile (Sect. 5). Results for H218O can
be found in the online appendix.
The H2O line profiles shown in Figs. 5 and 6 all contain optically thin and optically thick parts as discussed in Sect. 3.4. Since the line wings of most transitions are optically thin, a ``bump'' is present in these wings at the velocity for which that particular line becomes optically thick. This velocity depends solely on the total column of water at this velocity and not on the luminosity. The height of this bump is determined by both the luminosity and the density profile. The line center changes according to the actual optical depth of both the dust and the water itself. Line centers can (i) be effectively thin and show a Gaussian profile, (ii) be dominated by a small region and be flat-topped, (iii) show a self-absorption feature determined by the optical depth of the line alone; (iv) have absorption into the dust continuum.
Our spherically symmetric envelope models have several limitations, which can affect the interpretation of observed line strengths.
Table 7:
Integrated intensity and peak brightness of lines with and without dust for a model with p=1.5,
![]() and
and
![]() cm-3.
cm-3.
![\begin{figure}
\par\includegraphics[angle=270,width=150pt]{images/duststructure_...
...udegraphics[angle=270,width=150pt]{images/duststructure_highdens.ps}\end{figure}](/articles/aa/full/2008/33/aa09426-08/Timg113.gif) |
Figure 8:
Cartoon of protostellar envelope models. For two different models, the |
| Open with DEXTER | |
The presence of dust in protostellar envelopes influences water emission lines significantly in two ways, as can be seen in Table 7. First, the dust can become optically thick,
preventing water emission from deep in the envelope to escape. Second,
the far-infrared radiation can pump the water lines. Dust becomes
optically thick at specific columns, depending on the value of the
opacity, ![]() ,
at a given frequency (see Fig. 5c in
Ossenkopf & Henning 1994, for the precise relation).
Since
,
at a given frequency (see Fig. 5c in
Ossenkopf & Henning 1994, for the precise relation).
Since
![]() ,
with the dust opacity index
,
with the dust opacity index ![]() typically 1.5, this is especially likely at higher frequencies. Column 4 of Table 8 shows the total gas and dust column densities needed to reach a dust optical depth equal to 1 for each line.
typically 1.5, this is especially likely at higher frequencies. Column 4 of Table 8 shows the total gas and dust column densities needed to reach a dust optical depth equal to 1 for each line.
Table 8:
The dust properties at selected water line frequencies for four typical models.
The column density
![]() required to produce
required to produce ![]() for the dust at each frequency
is given with the corresponding radii and temperatures.
for the dust at each frequency
is given with the corresponding radii and temperatures.
Figure 8 illustrates this effect in a cartoon for two
different envelope models. Two models, one with low density (low
![]() )
and one with high density
(high
)
and one with high density
(high
![]() ), are compared for two
ground-state lines. The dust at 557 GHz only becomes optically thick
for the more massive envelope due to very high column densities, while
the low-density model remains optically thin throughout. The
), are compared for two
ground-state lines. The dust at 557 GHz only becomes optically thick
for the more massive envelope due to very high column densities, while
the low-density model remains optically thin throughout. The ![]() surfaces correspond to temperatures well over 100 K. Since the 557 GHz
water line is optically thick at lower columns, the dust will have no
effect on this line, except for weakening the line due to dust
absorption. Even the H218O column is large enough to prevent the
dust opacity from influencing the 548 GHz line. In contrast, the dust
at 1669 GHz becomes optically thick at a much smaller column, which
corresponds to a radius and temperature much farther out into the
envelope. The actual radius depends on the model in question.
In the low-density model, the dust only turns optically thick
at radii close to the 100 K water evaporation radius, while dust in
the high-density model already obscures the line in the outer regions
of the envelope. Optically thin lines at this frequency will not be
able to probe the warm inner region, since the optically thick dust
effectively absorbs all water line emission.
surfaces correspond to temperatures well over 100 K. Since the 557 GHz
water line is optically thick at lower columns, the dust will have no
effect on this line, except for weakening the line due to dust
absorption. Even the H218O column is large enough to prevent the
dust opacity from influencing the 548 GHz line. In contrast, the dust
at 1669 GHz becomes optically thick at a much smaller column, which
corresponds to a radius and temperature much farther out into the
envelope. The actual radius depends on the model in question.
In the low-density model, the dust only turns optically thick
at radii close to the 100 K water evaporation radius, while dust in
the high-density model already obscures the line in the outer regions
of the envelope. Optically thin lines at this frequency will not be
able to probe the warm inner region, since the optically thick dust
effectively absorbs all water line emission.
Figure 9 shows example spectra of the 110-101line at 557 GHz, 212-101 line at 1669 GHz and the
312-303 line at 1097 GHz for a model with
![]() ,
,
![]() cm-3, p=1.5,
X0=10-4, and
cm-3, p=1.5,
X0=10-4, and
![]() ,
with and without dust. The spectra with dust
are significantly weaker by up to 50%, even for optically thin dust
at 557 GHz, since dust within the line of sight absorbs the water line
photons. Lines that are optically thin at a frequency where optically thick
dust exists are weaker by factors up to a few or more if dust is
present, due to less water being ``visible''. Optically thin lines can
be pumped by far-infrared dust radiation coming from the region at
radii larger than the
,
with and without dust. The spectra with dust
are significantly weaker by up to 50%, even for optically thin dust
at 557 GHz, since dust within the line of sight absorbs the water line
photons. Lines that are optically thin at a frequency where optically thick
dust exists are weaker by factors up to a few or more if dust is
present, due to less water being ``visible''. Optically thin lines can
be pumped by far-infrared dust radiation coming from the region at
radii larger than the ![]() surface of the dust at the frequency of
the line.
surface of the dust at the frequency of
the line.
For each envelope model, the column density of dust depends on a
combination of luminosity L (through the location of
![]() ,
Table 2) and envelope structure parameters n0 and p. If the
,
Table 2) and envelope structure parameters n0 and p. If the
![]() surface is approximated as a hard surface where all water
photons are absorbed, a typical temperature can be extracted for each
combination of L, n0, and p. This temperature is the upper limit
to which water lines can probe for each model before dust becomes
optically thick. Table 8 presents the
surface is approximated as a hard surface where all water
photons are absorbed, a typical temperature can be extracted for each
combination of L, n0, and p. This temperature is the upper limit
to which water lines can probe for each model before dust becomes
optically thick. Table 8 presents the ![]() temperatures for four astronomically distinct models, based on the
results from Table 6 of Jørgensen et al. (2002). Model 1, with
temperatures for four astronomically distinct models, based on the
results from Table 6 of Jørgensen et al. (2002). Model 1, with
![]() ,
p=1.5, and
,
p=1.5, and
![]() cm-3, corresponds to a very young Class 0 YSO, which is dominated by a large, cold, and
massive protostellar envelope. A good example is the well-studied NGC
1333 IRAS 4B source in the Perseus molecular cloud. Lines with a
frequency above 1600 GHz are unable to probe the region with T>100 K. Dust is optically thin throughout the envelope for frequencies
lower than a 1000 GHz. Model 2, with
cm-3, corresponds to a very young Class 0 YSO, which is dominated by a large, cold, and
massive protostellar envelope. A good example is the well-studied NGC
1333 IRAS 4B source in the Perseus molecular cloud. Lines with a
frequency above 1600 GHz are unable to probe the region with T>100 K. Dust is optically thin throughout the envelope for frequencies
lower than a 1000 GHz. Model 2, with
![]() , p=2 and
, p=2 and
![]() cm-3, has similar parameters but its mass is
more centrally condensed. Due to the very high column densities, dust
becomes optically thick at all frequencies above 700 GHz, making it
even more difficult to probe the central warm region than in Model 1. Highly excited water lines are effectively shielded from observers
within this envelope at all frequencies. The third model,
cm-3, has similar parameters but its mass is
more centrally condensed. Due to the very high column densities, dust
becomes optically thick at all frequencies above 700 GHz, making it
even more difficult to probe the central warm region than in Model 1. Highly excited water lines are effectively shielded from observers
within this envelope at all frequencies. The third model,
![]() ,
p=2,
,
p=2,
![]() cm-3, corresponds to a
more evolved source with a low luminosity and a small envelope with
most of the mass concentrated in the center due to a steep density
profile. The relative amount of warm gas in this envelope is
significantly higher. Such a model would correspond to most Class I
sources, e.g., TMC-1A. The last model included has
cm-3, corresponds to a
more evolved source with a low luminosity and a small envelope with
most of the mass concentrated in the center due to a steep density
profile. The relative amount of warm gas in this envelope is
significantly higher. Such a model would correspond to most Class I
sources, e.g., TMC-1A. The last model included has
![]() ,
p=1.5, and
,
p=1.5, and
![]() cm-3 which corresponds to a
higher luminosity source, but with a low total mass. The mass of the
envelope is distributed over larger radii and the luminosity is
higher. For these last two models, dust will not hide the inner parts
of the envelope at all. Only the very warm region (T> 150 K) is
veiled near the inner radius of Model 3.
cm-3 which corresponds to a
higher luminosity source, but with a low total mass. The mass of the
envelope is distributed over larger radii and the luminosity is
higher. For these last two models, dust will not hide the inner parts
of the envelope at all. Only the very warm region (T> 150 K) is
veiled near the inner radius of Model 3.
The structure of micro-turbulence, defined in our models as a velocity dispersion, during the embedded phases of star formation is not well known, and theoretical models do not yet agree on a correct treatment. A good review of the theoretical considerations and problems is given in Ward-Thompson & Buckley (2001, their Sect. 3.2). Jørgensen (2004) concludes that the inclusion of micro-turbulence as a velocity dispersion gives a more accurate reproduction of line intensities and profiles as opposed to the inclusion of infall (Jørgensen et al. 2005). Ward-Thompson & Buckley (2001, Sect. 4.6) test different values of micro-turbulence, as well as different power-law values for the variation of micro-turbulence with radius. This results in a large variation in the molecular line profiles of CS and HCO+. Similarly, Fig. 10 shows that the choice of the velocity dispersion can have a strong effect on all water lines, both optically thick and thin. All three lines (557, 1669, and 1097 GHz) show large differences in both line profile and in total integrated emission up to a factor of 3, when the velocity dispersion is varied between 0.83 (b=0.5), 1.67 (b=1) and 3.34 (b=2) km s-1. Absorption both into the continuum and in the line are broader for higher values of micro-turbulence, while peak separation increases with increased velocity dispersion. Optically thin lines and line wings broaden if b is larger. Such effects are similar to those found by Ward-Thompson & Buckley (2001).
For molecular lines in low-mass protostellar envelopes,
Ward-Thompson & Buckley (2001) and Jørgensen et al. (2005) both adopt a
constant value for the micro-turbulence with radius. In our case, a
velocity dispersion,
![]() km s-1 (b=1 km s-1), has been chosen to best reproduce line emission for a
wide variety of molecules in sources such as L483, including CO, CS,
but also complex molecules such as H2CO and CH3OH, tracing both
the warm and cold regions. We recommend that for the modeling of
water lines from specific sources, the velocity dispersion for the
cloud in question be adopted as derived from other molecular lines.
km s-1 (b=1 km s-1), has been chosen to best reproduce line emission for a
wide variety of molecules in sources such as L483, including CO, CS,
but also complex molecules such as H2CO and CH3OH, tracing both
the warm and cold regions. We recommend that for the modeling of
water lines from specific sources, the velocity dispersion for the
cloud in question be adopted as derived from other molecular lines.
The conclusions presented in previous paragraphs can be compared to current observational studies. However, due to the approximations used within the models and the unique combinations of parameters for individual sources, it is recommended that these models be used only as a starting point for interpreting water emission of protostellar envelopes from specific sources. As discussed in Sect. 4.6, there are several factors that will complicate any analysis of observed water lines. To compare the envelope models presented above with any individual observation other than those from Herschel, the line intensities have to be corrected for the actual beam size of the telescope.
Water has been detected in several low-mass YSOs (both Class 0 and
Class I) with ISO-LWS such as NGC 1333 IRAS 2/4, IRAS 16293-2422,
Elias 29, L 1448, L 483, and SSV 13 (e.g., Giannini et al. 2001; Nisini et al. 1999; Maret et al. 2002; Ceccarelli et al. 1999; Liseau et al. 1996). Up
to 14 water lines were detected, ranging from 180.5 ![]() m to 67.3
m to 67.3 ![]() m. In most sources the total number of lines is significantly
lower, but sufficient for proving the existence of water. For example,
only a single line was detected for the Class I source Elias 29
(Ceccarelli et al. 1999).
m. In most sources the total number of lines is significantly
lower, but sufficient for proving the existence of water. For example,
only a single line was detected for the Class I source Elias 29
(Ceccarelli et al. 1999).
As an illustration, we consider the case of NGC 1333 IRAS4A/B, for
which Maret et al. (2002) report the emission of 14 water lines, together
with high-J CO, OH, [O I], and [C II]. A model was put forward to explain the
origin of these FIR lines using a collapsing envelope model without
an outflow. Based on the model developed by Ceccarelli et al. (1996), the
envelope and stellar parameters were derived from the best fit model
to the 14 water lines. The water abundances in the envelope were found to
include a jump at 100 K with a best fit of
![]() and
and
![]() .
A lower inner abundance is excluded by their
model results,
but a higher X0 abundance of
the order of
.
A lower inner abundance is excluded by their
model results,
but a higher X0 abundance of
the order of
![]() cannot be excluded.
cannot be excluded.
| |
Figure 9:
Example spectra of the 110-101 557 GHz line (
left), 212-101 1669 GHz line ( middle) and 312-303 1097 GHz line ( right) for a model with p=1.5,
|
| Open with DEXTER | |
| |
Figure 10:
Example spectra of the 110-101 557 GHz line ( left), 212-101 1669 GHz line ( middle), and 312-303 1097 GHz line ( right) for a model with
p=1.5,
|
| Open with DEXTER | |
The physical parameters derived by Jørgensen et al. (2002) and abundances
proposed by Maret et al. (2002) correspond best with our model to n0=106 cm-3,
![]() ,
and p=1.5 with abundances 10-6 for X0 and 10-6/10-7 for
,
and p=1.5 with abundances 10-6 for X0 and 10-6/10-7 for
![]() .
However, our predicted line strengths differ from the observed and
predicted line strengths in Maret et al. (2002), especially for low
excitation lines. Our 221-212 and 212-101
predictions are 0.5 10-20 and
.
However, our predicted line strengths differ from the observed and
predicted line strengths in Maret et al. (2002), especially for low
excitation lines. Our 221-212 and 212-101
predictions are 0.5 10-20 and
![]() W cm-2 for the
10-6/10-7 abundance combination within the ISO-LWS beam,
significantly lower than the observed values of 11 and
W cm-2 for the
10-6/10-7 abundance combination within the ISO-LWS beam,
significantly lower than the observed values of 11 and
![]() W cm-2. Although an inner abundance of 10-4 produces brighter lines for the presented models, these lines are still an order of magnitude lower than the observed fluxes in Maret et al. (2002).
The most likely explanation is the different treatment of dust between
the two models, which lowers the fluxes of the high-frequency lines in
our case. However, this also suggests that our models can only
explain the ISO-LWS fluxes if there are cavities in the envelopes
through which the photons can escape. Recent results with the Spitzer
Space Telescope show numerous spectrally unresolved water lines from
20 to 30
W cm-2. Although an inner abundance of 10-4 produces brighter lines for the presented models, these lines are still an order of magnitude lower than the observed fluxes in Maret et al. (2002).
The most likely explanation is the different treatment of dust between
the two models, which lowers the fluxes of the high-frequency lines in
our case. However, this also suggests that our models can only
explain the ISO-LWS fluxes if there are cavities in the envelopes
through which the photons can escape. Recent results with the Spitzer
Space Telescope show numerous spectrally unresolved water lines from
20 to 30 ![]() m, which suggest that NGC 1333 IRAS 4B is indeed viewed
almost face-on, allowing the ro-vibrational lines to escape the
protostellar system unhindered along the outflow axis
(Watson et al. 2007). This can also help the longer wavelength lines
coming from the inner envelope. Another possibility is that
significant contributions come from large-scale outflows. This is
confirmed by SWAS (see Sect. 6.2).
m, which suggest that NGC 1333 IRAS 4B is indeed viewed
almost face-on, allowing the ro-vibrational lines to escape the
protostellar system unhindered along the outflow axis
(Watson et al. 2007). This can also help the longer wavelength lines
coming from the inner envelope. Another possibility is that
significant contributions come from large-scale outflows. This is
confirmed by SWAS (see Sect. 6.2).
SWAS![]() observed only the
ground-state transition of o-H2O at 557 GHz and o-H218O at 548 GHz. Although the beam of SWAS (
observed only the
ground-state transition of o-H2O at 557 GHz and o-H218O at 548 GHz. Although the beam of SWAS (
![]() )
is significantly larger than for ISO-LWS, the increased spectral resolution of better than 1 km s-1 spectrally resolves most lines in starforming regions.
)
is significantly larger than for ISO-LWS, the increased spectral resolution of better than 1 km s-1 spectrally resolves most lines in starforming regions.
SWAS observed the NGC 1333 IRAS4 region (Neufeld et al. 2000; Bergin et al. 2003)
where, contrary to the analysis of Maret et al. (2002), they observed a
wide (24.4 km s-1) and bright (
![]() -1.9 K km s-1) line. It was concluded that these lines originate within the outflow of one or more sources inside the NGC 1333 region. The model proposed by Maret et al. (2002) would have produced a narrow (<4 km s-1) and weak (0.02-0.04 K km s-1) 557 GHz line for each source contained within the beam. Our grid gives a typical integrated intensity within a SWAS beam of
-1.9 K km s-1) line. It was concluded that these lines originate within the outflow of one or more sources inside the NGC 1333 region. The model proposed by Maret et al. (2002) would have produced a narrow (<4 km s-1) and weak (0.02-0.04 K km s-1) 557 GHz line for each source contained within the beam. Our grid gives a typical integrated intensity within a SWAS beam of
![]() K km s-1 for a X0/
K km s-1 for a X0/![]() combination of 10-4/10-6 with a typical line width of 6 km s-1.
combination of 10-4/10-6 with a typical line width of 6 km s-1.
Ashby et al. (2000) report on SWAS data for B335, an isolated Class 0
source with a 3![]() upper limit of <0.06 K km s-1. Evans et al. (2005) used a wide variety of molecular emission lines to model the chemistry and physical structure of this source.
The low luminosity (4.5
upper limit of <0.06 K km s-1. Evans et al. (2005) used a wide variety of molecular emission lines to model the chemistry and physical structure of this source.
The low luminosity (4.5 ![]() )
and low density (
)
and low density (
![]() cm-3) found by Evans et al. (2005) indicate that this class 0 source would be represented best by a model
with p=1.5,
cm-3) found by Evans et al. (2005) indicate that this class 0 source would be represented best by a model
with p=1.5,
![]() and
and
![]() cm-3.
Our predicted 557 GHz line strength corrected for the much larger SWAS beam is 0.02-0.06 K km s-1 for outer abundances from 10-8 to 10-6, just below the upper limits from SWAS. The only model that would have been detectable with SWAS has a constant abundance of 10-6. The high jump abundance model with
X0=10-4 and
cm-3.
Our predicted 557 GHz line strength corrected for the much larger SWAS beam is 0.02-0.06 K km s-1 for outer abundances from 10-8 to 10-6, just below the upper limits from SWAS. The only model that would have been detectable with SWAS has a constant abundance of 10-6. The high jump abundance model with
X0=10-4 and
![]() cannot be ruled out, since most of the line is self-absorbed. A similar conclusion holds for most other Class 0 sources detected with SWAS.
cannot be ruled out, since most of the line is self-absorbed. A similar conclusion holds for most other Class 0 sources detected with SWAS.
Using the SWAS archive![]() , upper
limits were found on several Class I sources,
including RCrA IRS 5 and 7.
Only upper limits of 20-50 mK in peak temperature could be derived. These
observed limits are higher by up to an order of magnitude than the
predictions presented in Sect. 4 for models that would fit the physical
parameters of Class I sources.
The cold envelope material is constrained to 10''-30'', a small
region within the SWAS beam. Thus, our models are consistent with the
scarce observational data on Class I sources.
, upper
limits were found on several Class I sources,
including RCrA IRS 5 and 7.
Only upper limits of 20-50 mK in peak temperature could be derived. These
observed limits are higher by up to an order of magnitude than the
predictions presented in Sect. 4 for models that would fit the physical
parameters of Class I sources.
The cold envelope material is constrained to 10''-30'', a small
region within the SWAS beam. Thus, our models are consistent with the
scarce observational data on Class I sources.
In summary, both the ISO and SWAS data stress the need for Herschel Space Observatory data to properly constrain the origin of the observed H2O emission and distinguish large-scale and outflow contributions from the emission originating in the quiescent gas of the protostellar envelope.
This paper presents several models that examine the excitation of water
and its oxygen-18 isotopologue in envelopes around low-mass
protostars, with parameters covering the entire range of luminosity
and envelope characteristics of observed Class 0 and I sources. A
model for the Class 0 source L 483 was used to illustrate the
dependence of rotational water lines on the water abundances in the
inner (T>100 K) region X0 and outer (T<100 K) region
![]() .
In turn, a broader grid of models was explored for the
full range of parameters and likely abundances. The main conclusions
follow.
.
In turn, a broader grid of models was explored for the
full range of parameters and likely abundances. The main conclusions
follow.
Acknowledgements
T.v.K. would like to thank Dieter Poelman, Floris van der Tak, and Antonio Crapsi for valuable discussion concerning YSO envelope modeling in general and the use of RATRAN. T.v.K. and astrochemistry at Leiden Observatory are supported by a Spinoza grant and by grant 614.041.004 from the Netherlands Organization for Scientific Research (NWO).
![\begin{figure}
\par\includegraphics[width=140pt]{pictures/p31_c.ps}\includegraph...
...s}\includegraphics[width=140pt]{pictures/p1_c.ps}\hspace*{2.5cm}}
\end{figure}](/articles/aa/full/2008/33/aa09426-08/Timg140.gif) |
Figure 11:
Contour plots of the integrated intensity of the L 483 models as a function of inner (X0) and outer (
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=140pt]{pictures/o9_c.ps}\includegraphi...
...t]{pictures/o2_c.ps}\includegraphics[width=140pt]{pictures/o1_c.ps}
\end{figure}](/articles/aa/full/2008/33/aa09426-08/Timg141.gif) |
Figure 12:
Contour plots of the integrated intensity of the L 483 models as a function of inner (X0) and outer (
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=140pt]{pictures/18p31_c.ps}\includegra...
...}\includegraphics[width=140pt]{pictures/18p1_c.ps}\hspace*{2.5cm}}\end{figure}](/articles/aa/full/2008/33/aa09426-08/Timg142.gif) |
Figure 13:
Contour plots of the integrated intensity of the L 483 models as a function of inner (X0) and outer (
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=140pt]{pictures/18o9_c.ps}\includegrap...
...ictures/18o2_c.ps}\includegraphics[width=140pt]{pictures/18o1_c.ps}
\end{figure}](/articles/aa/full/2008/33/aa09426-08/Timg143.gif) |
Figure 14:
Contour plots of the integrated intensity of the L 483 models as a function of inner (X0) and outer (
|
| Open with DEXTER | |
Table 9:
Integrated intensities,
![]() [K km s-1], for H2O lines in the wide parameter grid for all abundances. Ortho lines for p=1.5.
[K km s-1], for H2O lines in the wide parameter grid for all abundances. Ortho lines for p=1.5.
Table 10:
Integrated intensities,
![]() [K km s-1], for H2O lines in the wide parameter grid for all abundances, Ortho lines for p=2.0.
[K km s-1], for H2O lines in the wide parameter grid for all abundances, Ortho lines for p=2.0.
Table 11:
Integrated intensities,
![]() [K km s-1], for H2O lines in the wide parameter grid for all abundances. Para lines for p=1.5.
[K km s-1], for H2O lines in the wide parameter grid for all abundances. Para lines for p=1.5.
Table 12:
Integrated intensities,
![]() [K km s-1], for H2O lines in the wide parameter grid for all abundances for para p =2.0.
[K km s-1], for H2O lines in the wide parameter grid for all abundances for para p =2.0.