A&A 467, 207-216 (2007)
DOI: 10.1051/0004-6361:20065682
T. Pillai1,![]() - F. Wyrowski1 - J. Hatchell2 - A. G. Gibb3 - M. A. Thompson4
- F. Wyrowski1 - J. Hatchell2 - A. G. Gibb3 - M. A. Thompson4
1 - Max-Planck-Institut für Radioastronomie, Auf dem Hügel 69, 53121 Bonn, Germany
2 - School of Physics, University of Exeter, Stocker Road, Exeter EX4 4QL, UK
3 - Department of Physics & Astronomy, University of British Columbia, Vancouver, BC, V6T 1Z1, Canada
4 - Centre for Astrophysics Research, Science & Technology Research Institute, University of Hertfordshire, College Lane, Hatfield, AL10 9AB, UK
Received 23 May 2006 / Accepted 5 February 2007
Abstract
Aims. UltraCompact H II regions are signposts of high-mass star formation. Since high-mass star formation occurs in clusters, one expects to find even earlier phases of massive star formation in the vicinity of UltraCompact H II regions. Here, we study the amount of deuteration and depletion toward pre/protocluster clumps found in a wide-field (
![]() arcmin) census of clouds in 32 massive star-forming regions that are known to harbour UCH II regions.
arcmin) census of clouds in 32 massive star-forming regions that are known to harbour UCH II regions.
Methods. We determine the column density of
![]() ,
,
![]() ,
CO,
,
CO,
![]() ,
and
,
and
![]() lines. We used the
(J,K) = (1, 1) and (2, 2) inversion transitions of
lines. We used the
(J,K) = (1, 1) and (2, 2) inversion transitions of
![]() to constrain the gas temperatures.
to constrain the gas temperatures.
Results. We find that 65% of the observed sources have strong
![]() emission and more than 50% of the sources exhibit a high degree of deuteration, (
emission and more than 50% of the sources exhibit a high degree of deuteration, (
![]() ), 0.7 being the highest observed deuteration of
), 0.7 being the highest observed deuteration of
![]() reported to date. Our search for
reported to date. Our search for
![]() in two sources did not result in a detection. The enhancement in deuteration coincides with moderate CO depletion onto dust grains. There is no evidence of a correlation between the two processes, though an underlying correlation cannot be ruled out as the depletion factor is very likely to be only a lower limit. Based on simultaneously observed
in two sources did not result in a detection. The enhancement in deuteration coincides with moderate CO depletion onto dust grains. There is no evidence of a correlation between the two processes, though an underlying correlation cannot be ruled out as the depletion factor is very likely to be only a lower limit. Based on simultaneously observed
![]() and
and
![]() (J=1-0) lines, we derive a high abundance ratio of
(J=1-0) lines, we derive a high abundance ratio of
![]() to
to
![]() ,
which might indicate anomalous ratios of C and N isotopes relative to those derived toward the local ISM.
,
which might indicate anomalous ratios of C and N isotopes relative to those derived toward the local ISM.
Conclusions. We find CO depletion and high deuteration towards cold cores in massive star forming regions. Therefore, these are good candidates for sources at the early phases of massive star formation. While our sensitive upper limits on
![]() do not prove the predictions of the gas-phase and grain chemistry models wrong, an enhancement of
do not prove the predictions of the gas-phase and grain chemistry models wrong, an enhancement of ![]() 104 over the cosmic D/H ratio from
104 over the cosmic D/H ratio from
![]() warrants explanation.
warrants explanation.
Key words: stars: formation - astrobiology - molecular data - methods: observational - ISM: clouds - radio lines: ISM
The earliest phases of high mass star formation are still poorly
understood. The prevalent theory is that massive stars are born in
dense clumps within giant molecular clouds (GMCs), where the presence
of UltraCompact H II regions (UCH II) identifies massive stars which
have already begun to ionize their surroundings. Observations
(Cesaroni et al. 1994,1998) have shown that these
are often associated with warm (T>100 K), compact (<0.1 pc) and
very dense (
![]()
![]() )
cores known as hot molecular
cores (HMCs). An evolutionary sequence has been suggested based on
recent observations (Codella et al. 2004;
Beuther & Shepherd 2005) with the HMC stage immediately
preceding the formation of UCH II regions. But the stage before hot cores -
the precluster and early protocluster phases of massive star formation
- have not yet been studied. Since many UCH II regions are
located in clusters, one expects to find even earlier phases of
massive star formation, and the raw material out of which massive stars
or star clusters form, in the vicinity of UCH IIs (Thompson et al. 2006).
)
cores known as hot molecular
cores (HMCs). An evolutionary sequence has been suggested based on
recent observations (Codella et al. 2004;
Beuther & Shepherd 2005) with the HMC stage immediately
preceding the formation of UCH II regions. But the stage before hot cores -
the precluster and early protocluster phases of massive star formation
- have not yet been studied. Since many UCH II regions are
located in clusters, one expects to find even earlier phases of
massive star formation, and the raw material out of which massive stars
or star clusters form, in the vicinity of UCH IIs (Thompson et al. 2006).
This has prompted us to embark upon a program to search for massive
pre/protocluster clumps by taking a wide-field (
![]() arcmin) census of clouds in 32 massive star-forming regions, harbouring UCH II regions (Wood & Churchwell 1989). Our program is known as SCAMPS (the SCUBA Massive
Pre/Protocluster core Survey; Thompson et al. 2005; Thompson et al. 2007, in prep.).
arcmin) census of clouds in 32 massive star-forming regions, harbouring UCH II regions (Wood & Churchwell 1989). Our program is known as SCAMPS (the SCUBA Massive
Pre/Protocluster core Survey; Thompson et al. 2005; Thompson et al. 2007, in prep.).
We discovered a multitude of secondary, cold condensations and warmer
clumps that might contain heavily embedded massive protostars. Many of
the sources are seen as dark patches in MSX infrared images of the
region, infrared dark clouds (IRDCs; Menten et al. 2005). As a result these clumps must have dust temperatures below 30 K (as evidenced by MIR upper limits) and have masses of a few 100 to 1000 ![]() .
These clumps thus could be in a colder pre-protostellar phase.
.
These clumps thus could be in a colder pre-protostellar phase.
In order to study the physical and chemical conditions of these
clumps, we carried out a multi-wavelength survey toward them in
various molecular tracers. In this study, we also included 9 sources
which were selected on the basis of the MIR extinction (IRDCs) and
followed up later with submillimeter dust continuum emission and
millimeter rotational lines of H2CO (Carey et al. 1998). We have
recently reported a study of ammonia in this sample
(Pillai et al. 2006). Here, we report on our study using ammonia to
probe the temperature and deuteration in the clumps and CO to estimate
depletion of neutral molecules from the gas phase. Depletion has
proved to be a good tracer of low-mass pre-stellar cores
(Bacmann et al. 2003 and
Crapsi et al. 2005), and
![]() is an important
tool in measuring the physical conditions in molecular clouds and can
be used to confirm the low temperatures and high densities required
for depletion (Ho & Townes 1983). Since only the lowest
is an important
tool in measuring the physical conditions in molecular clouds and can
be used to confirm the low temperatures and high densities required
for depletion (Ho & Townes 1983). Since only the lowest
![]() energy
levels are expected to be populated for cold dark clouds (T<20 K),
their physical conditions can be probed using the (1, 1) and (2, 2)
inversion transitions in the metastable (J,K) rotational levels of
ammonia. Radiative transitions between different K-ladders are
forbidden, therefore the lowest levels are populated only via
collisions. The optical depth can be determined from the ratio of the
hyperfine satellites. Thus, the population of the different levels can
be estimated and hence the temperature of the gas determined.
energy
levels are expected to be populated for cold dark clouds (T<20 K),
their physical conditions can be probed using the (1, 1) and (2, 2)
inversion transitions in the metastable (J,K) rotational levels of
ammonia. Radiative transitions between different K-ladders are
forbidden, therefore the lowest levels are populated only via
collisions. The optical depth can be determined from the ratio of the
hyperfine satellites. Thus, the population of the different levels can
be estimated and hence the temperature of the gas determined.
![]() is observed to be an excellent tracer
of the dense gas where many other molecules would have heavily
depleted (Tafalla et al. 2004). In addition, recent chemical models reveal that
is observed to be an excellent tracer
of the dense gas where many other molecules would have heavily
depleted (Tafalla et al. 2004). In addition, recent chemical models reveal that
![]() (and also N2H+), does not deplete from the gas phase for the
densities observed in dark clouds (<106
(and also N2H+), does not deplete from the gas phase for the
densities observed in dark clouds (<106
![]() ;
Bergin & Langer 1997). However in the light of recent experiments of the desorption of CO and N2 at temperatures relevant to dense cores, the relative difference between the derived CO and N2 binding energies is found to be significantly less than that currently adopted in astrochemical models (Öberg et al. 2005). Therefore, the observed non-depletion of
;
Bergin & Langer 1997). However in the light of recent experiments of the desorption of CO and N2 at temperatures relevant to dense cores, the relative difference between the derived CO and N2 binding energies is found to be significantly less than that currently adopted in astrochemical models (Öberg et al. 2005). Therefore, the observed non-depletion of
![]() and N2H+ during the early formation of a massive cluster remains a "mystery''.
and N2H+ during the early formation of a massive cluster remains a "mystery''.
High densities in the earliest phase are expected to enhance depletion of molecules (mainly CO) onto grains (Bacmann et al. 2003). The freeze out of abundant gas phase molecules along with the low temperatures (![]() 20 K) prevalent in these clumps leads to a high degree of deuteration
(Flower et al. 2005; Roueff et al. 2005; Hatchell 2003; Shah & Wootten 2001; Saito et al. 2000). Hence, the estimation of deuteration and
depletion in clumps can be used as a chemical and physical chronometer.
20 K) prevalent in these clumps leads to a high degree of deuteration
(Flower et al. 2005; Roueff et al. 2005; Hatchell 2003; Shah & Wootten 2001; Saito et al. 2000). Hence, the estimation of deuteration and
depletion in clumps can be used as a chemical and physical chronometer.
In this paper we investigate the
![]() temperature and deuteration in
our candidate pre/protocluster cores using observations with the
Effelsberg 100 m and IRAM 30 m telescopes.
In Sect. 2, we describe our single dish
observations.
We also discuss the data reduction and present the derived physical
parameters for different molecules. In Sect. 3, we
show that candidate pre/protocluster clumps exhibit very high deuteration and
depletion. The fractionation of
temperature and deuteration in
our candidate pre/protocluster cores using observations with the
Effelsberg 100 m and IRAM 30 m telescopes.
In Sect. 2, we describe our single dish
observations.
We also discuss the data reduction and present the derived physical
parameters for different molecules. In Sect. 3, we
show that candidate pre/protocluster clumps exhibit very high deuteration and
depletion. The fractionation of
![]() is compared with depletion of CO
from the gas phase. The possible origin of deuterated species and the
variation of deuteration with gas temperature is also discussed.
HCN was also observed as part of the 30 m observations and we
conclude the discussion with our
interpretation of the HCN isotopic abundance with galactic distance.
is compared with depletion of CO
from the gas phase. The possible origin of deuterated species and the
variation of deuteration with gas temperature is also discussed.
HCN was also observed as part of the 30 m observations and we
conclude the discussion with our
interpretation of the HCN isotopic abundance with galactic distance.
Table 1: Parameters of observed rotational transitions.
In this section we present the results of single dish observations of
![]() ,
,
![]() ,
CO and HCN lines on a sample of 23 SCAMPS sources and 9
IRDCs. The brightest compact submm sources with no MIR counterpart
were selected for these observations from our original catalogue of
the SCUBA fields. The parameters of the molecular transitions covered,
along with the observing setups are given in Table 1. In
Table 2, we give the source list. The derived
line parameters and the column densities are presented in Tables 3-6.
,
CO and HCN lines on a sample of 23 SCAMPS sources and 9
IRDCs. The brightest compact submm sources with no MIR counterpart
were selected for these observations from our original catalogue of
the SCUBA fields. The parameters of the molecular transitions covered,
along with the observing setups are given in Table 1. In
Table 2, we give the source list. The derived
line parameters and the column densities are presented in Tables 3-6.
Table 2: Positions and velocities of the observed sources. IRDC positions are taken from Carey et al. (1998).
The
![]() ,
,
![]() ,
,
![]() and
and
![]() observations were made at the IRAM 30 m telescope
observations were made at the IRAM 30 m telescope![]() on Pico Veleta in August 2003 toward the 32 candidate pre/protocluster clumps given in Table 2. We performed 9 point maps
with 10'' spacing around the peak to be able to compare, independently of the beam, lines at different frequencies. All line parameters listed are averaged over the map.
on Pico Veleta in August 2003 toward the 32 candidate pre/protocluster clumps given in Table 2. We performed 9 point maps
with 10'' spacing around the peak to be able to compare, independently of the beam, lines at different frequencies. All line parameters listed are averaged over the map.
Individual positions were observed with an integration time of 2 minutes per position in the position switch mode. The receivers A100, B100, A230 and B230 were tuned to 86.13, 109.975, 219.56 and 231.32 GHz respectively.
The VESPA autocorrelator was used at the backend, with
a spectral resolution of 40 kHz and 320 kHz at 100 and 230 GHz
respectively. We had average summer weather conditions with a maximum
system temperature of 248 K at 110 GHz. Towards selected sources we also have
![]() (J=2-1) and
(J=2-1) and
![]() (110-101) observations. The half power beam width (HPBW) of
the 30 m telescope is 22'' at 110 GHz and 11'' at 230 GHz. The main
beam efficiency at these frequencies is 0.75 and 0.52, respectively.
(110-101) observations. The half power beam width (HPBW) of
the 30 m telescope is 22'' at 110 GHz and 11'' at 230 GHz. The main
beam efficiency at these frequencies is 0.75 and 0.52, respectively.
Table 3:
![]() and
and
![]() column densities, rotational temperature and fractionation.
column densities, rotational temperature and fractionation.
We observed the
![]() (1, 1) and (2, 2) transitions with the Effelsberg
100 m telescope
(1, 1) and (2, 2) transitions with the Effelsberg
100 m telescope ![]() in April 2004 for the 23 sources listed in Table 2.
Two of the sources were re-observed because of baseline problems with the receiver.
With the AK 8192 backend, we were able to observe the (1, 1), (2, 2),
(3, 3) and (4, 4) transitions in both polarisations simultaneously using
the K-band receiver. With 8 subunits of 10 MHz bandwidth, the
resulting spectral resolution was
in April 2004 for the 23 sources listed in Table 2.
Two of the sources were re-observed because of baseline problems with the receiver.
With the AK 8192 backend, we were able to observe the (1, 1), (2, 2),
(3, 3) and (4, 4) transitions in both polarisations simultaneously using
the K-band receiver. With 8 subunits of 10 MHz bandwidth, the
resulting spectral resolution was ![]() 0.25 km s-1. The
beam at the
0.25 km s-1. The
beam at the
![]() frequencies was 40''. The observations were
performed in the frequency switching mode. Pointing was checked at
hourly intervals by continuum scans on G10.62. We estimate the
pointing to be accurate to within 6''. The pointing scans were
used for the absolute flux calibration. The
frequencies was 40''. The observations were
performed in the frequency switching mode. Pointing was checked at
hourly intervals by continuum scans on G10.62. We estimate the
pointing to be accurate to within 6''. The pointing scans were
used for the absolute flux calibration. The
![]() observations toward the
9 IRDCs are reported in Pillai et al. (2006). Note that for
G12.19-0.12 and G29.97-0.05 we report the observations carried out in
October 2002 with a spectral resolution of
observations toward the
9 IRDCs are reported in Pillai et al. (2006). Note that for
G12.19-0.12 and G29.97-0.05 we report the observations carried out in
October 2002 with a spectral resolution of ![]() 1 km s-1.
1 km s-1.
The ratio of the brightness temperatures of the
![]() (1, 1) and (2, 2)
transitions, along with the optical depth, can be used to estimate the
rotational temperature. For temperatures <20 K, which are typical for
cold dark clouds, the rotational temperature closely follows the gas
kinetic temperature (Walmsley & Ungerechts 1983). Like
(1, 1) and (2, 2)
transitions, along with the optical depth, can be used to estimate the
rotational temperature. For temperatures <20 K, which are typical for
cold dark clouds, the rotational temperature closely follows the gas
kinetic temperature (Walmsley & Ungerechts 1983). Like
![]() ,
its
isotopologue
,
its
isotopologue
![]() also has hyperfines which allows the estimation of
optical depth and hence the column density. Thus
the fractionation ratio can be estimated assuming that
also has hyperfines which allows the estimation of
optical depth and hence the column density. Thus
the fractionation ratio can be estimated assuming that
![]() and
and
![]() are co-spatial and hence have the same gas temperature.
are co-spatial and hence have the same gas temperature.
![\begin{figure}
\par\includegraphics[height=18cm,angle=-90]{5682fig1.eps} \end{figure}](/articles/aa/full/2007/19/aa5682-06/Timg31.gif) |
Figure 1:
Left panel: comparison of the LSR velocities of
|
| Open with DEXTER | |
Out of the 32 sources that were observed,
![]() with hyperfines were detected in 22
sources with S/N ratio >5
with hyperfines were detected in 22
sources with S/N ratio >5![]() while we have a 100%
while we have a 100%
![]() (1, 1) and (2, 2) detection. While we detected the (3, 3) lines in most of the sources, the (4, 4) lines were not detected. The fits to the hyperfines for
(1, 1) and (2, 2) detection. While we detected the (3, 3) lines in most of the sources, the (4, 4) lines were not detected. The fits to the hyperfines for
![]() and
and
![]() were done using CLASS methods
were done using CLASS methods
![]() (1, 1) and HFS respectively (Forveille et al. 1989). The line parameters from the resultant fits are given
(1, 1) and HFS respectively (Forveille et al. 1989). The line parameters from the resultant fits are given![]() in Tables A.2 and A.3. For those sources
with a high uncertainty in the
in Tables A.2 and A.3. For those sources
with a high uncertainty in the
![]() optical depth, the main line
is fitted with a single Gaussian and the integrated intensity is
quoted. The spectra are shown in Fig. A.1.
optical depth, the main line
is fitted with a single Gaussian and the integrated intensity is
quoted. The spectra are shown in Fig. A.1.
The basic physical parameters, namely the rotational temperature, the
kinetic temperature and ammonia column density were derived using the
standard formulation for
![]() spectra (Bachiller et al. 1987). The
expressions used to estimate the column densities from the radiative
transfer equations for all other molecules including
spectra (Bachiller et al. 1987). The
expressions used to estimate the column densities from the radiative
transfer equations for all other molecules including
![]() are given
in Appendix A. The deduced physical parameters are given in
Table 3. The uncertainties given in brackets are
formal errors obtained by a Gaussian error propagation. We have
derived the
are given
in Appendix A. The deduced physical parameters are given in
Table 3. The uncertainties given in brackets are
formal errors obtained by a Gaussian error propagation. We have
derived the
![]() column density solely based on the ortho
transition. We assume that the ortho and para transitions are
in LTE.
column density solely based on the ortho
transition. We assume that the ortho and para transitions are
in LTE.
For the few cases with significant detection of the para state we find
that ratio of the integrated line intensity (
![]() )
is approximately 3 consistent with a thermalised ortho to para ratio of 3.
)
is approximately 3 consistent with a thermalised ortho to para ratio of 3.
For the column density determination of
![]() ,
we have averaged
over the 9 points of the map to compare to the
,
we have averaged
over the 9 points of the map to compare to the
![]() results. Essentially the resolution of the
results. Essentially the resolution of the
![]() observations has
been degraded to that of the
observations has
been degraded to that of the
![]() observations. A caveat is that a map obtained with 10
observations. A caveat is that a map obtained with 10
![]() spacing at the IRAM 30 m does
not completely sample the 40
spacing at the IRAM 30 m does
not completely sample the 40
![]() beam of the Effelsberg
telescope. However, it is very unlikely that there is significant
emission outside the beam of the Effelsberg telescope (i.e. its FWHM) because a)we find that
the brightest peak is always at the center of the map, b) box
averaging delivers a similar result to a 1 D Gaussian
weighted average c) the peak dust emission positions
have been chosen as the centre coordinates for these observations.
beam of the Effelsberg
telescope. However, it is very unlikely that there is significant
emission outside the beam of the Effelsberg telescope (i.e. its FWHM) because a)we find that
the brightest peak is always at the center of the map, b) box
averaging delivers a similar result to a 1 D Gaussian
weighted average c) the peak dust emission positions
have been chosen as the centre coordinates for these observations.
The
rotational temperatures are in a range from 11 to 23 K, with ammonia
column densities from 1 to 5
![]()
![]() .
We obtain
[
.
We obtain
[
![]() /
/
![]() ]
ratios from 0.004-0.66. A deuteration factor of 66%
in
]
ratios from 0.004-0.66. A deuteration factor of 66%
in
![]() is much larger than the largest reported value so
far,
is much larger than the largest reported value so
far, ![]() 33% by Hatchell (2003). In 10 out of the 22
sources with
33% by Hatchell (2003). In 10 out of the 22
sources with
![]() detection, we obtain abundance ratios
detection, we obtain abundance ratios ![]() 0.02
while the rest of the sources have a high degree of deuteration
(
0.02
while the rest of the sources have a high degree of deuteration
(![]() 13%). These 10 sources with low ratios show optically thin
13%). These 10 sources with low ratios show optically thin
![]() emission.
emission.
In Fig. 1, the correlation between the velocities and
line widths of the
![]() and
and
![]() emission is shown. Velocities and
line widths are clearly different in some sources, with the
emission is shown. Velocities and
line widths are clearly different in some sources, with the
![]() line widths being smaller in most cases. This could be either due to
line widths being smaller in most cases. This could be either due to
![]() and
and
![]() tracing different regions or the slightly different
beams at the two frequencies, in which case, clumping might contribute
to a larger line width. It is interesting to note that the critical
density of the reported
tracing different regions or the slightly different
beams at the two frequencies, in which case, clumping might contribute
to a larger line width. It is interesting to note that the critical
density of the reported
![]() transition is a factor 47 higher than
that of the corresponding
transition is a factor 47 higher than
that of the corresponding
![]() transition, assuming similar
collisional rates. However, a more likely explanation is that
transition, assuming similar
collisional rates. However, a more likely explanation is that
![]() could be originating from the more disturbed protocluster
environment, while
could be originating from the more disturbed protocluster
environment, while
![]() might be tracing the gas in precluster cores
(Pillai et al. in prep.).
might be tracing the gas in precluster cores
(Pillai et al. in prep.).
The
![]() (1-0) and (2-1) observations were performed simultaneously with
(1-0) and (2-1) observations were performed simultaneously with
![]() (
11,1-10,1). Figure A.2 shows the spectra toward all sources. Note that there are secondary features in the
(
11,1-10,1). Figure A.2 shows the spectra toward all sources. Note that there are secondary features in the
![]() spectra for a few sources, likely to be line of sight components not seen in
dense gas like
spectra for a few sources, likely to be line of sight components not seen in
dense gas like
![]() .
In Table A.4
.
In Table A.4![]() , we list the observed line parameters based on Gaussian fits, and, in Table 4, the column density and excitation temperature
estimates (see Appendix A) and the
, we list the observed line parameters based on Gaussian fits, and, in Table 4, the column density and excitation temperature
estimates (see Appendix A) and the
![]() abundances. The
abundances. The
![]() excitation temperature has been derived from the
excitation temperature has been derived from the
![]() J=1-0 and J=2-1 line ratios.
J=1-0 and J=2-1 line ratios.
Based on the dust continuum and CO observations for the observed sample, the depletion can be studied for the first time on a sample of massive clumps.
Recent observational studies on the condensation of CO in low mass prestellar
cores reveal that in the initial cold and dense evolutionary stage, CO
is heavily depleted onto the dust grains (Bacmann et al. 2002, Savva et al. 2003). The depletion factor ![]() is defined as
is defined as
The effective ![]() column density (Launhardt 1996) is calculated from
column density (Launhardt 1996) is calculated from
Table 4:
![]() column density and abundance from (J=1-0) and (J=2-1) transitions.
column density and abundance from (J=1-0) and (J=2-1) transitions.
In these dense clumps it is possible that the
![]() line may be optically thick and hence derived column densities could be a lower limit. In order to investigate this possibility, we observed the rarer isotopomer
line may be optically thick and hence derived column densities could be a lower limit. In order to investigate this possibility, we observed the rarer isotopomer
![]() toward two of our sources, G35.19-1.73 and G81.74+0.59 as
shown in Fig. 2. The line parameters are given in Table 5. In Sect. 3.1.1, we discuss how
toward two of our sources, G35.19-1.73 and G81.74+0.59 as
shown in Fig. 2. The line parameters are given in Table 5. In Sect. 3.1.1, we discuss how
![]() is used as a more reliable tracer of the optical depth.
is used as a more reliable tracer of the optical depth.
![\begin{figure}
\par\includegraphics[angle=-90,width=7cm,clip]{5682fig2.eps} \end{figure}](/articles/aa/full/2007/19/aa5682-06/Timg57.gif) |
Figure 2:
|
| Open with DEXTER | |
We also observed the isotopomeric species of HCN,
![]() and
and
![]() in
our 3 mm setup with the IRAM 30 m telescope.
in
our 3 mm setup with the IRAM 30 m telescope.
![]() was detected in
almost all sources except G19.30P1/P2 and G10.15-0.34. In
Fig. A.3, we show the spectra toward all sources
where both
was detected in
almost all sources except G19.30P1/P2 and G10.15-0.34. In
Fig. A.3, we show the spectra toward all sources
where both
![]() and
and
![]() are detected with sufficient S/N (
are detected with sufficient S/N (![]() 3
3![]() ). The
). The
![]() line has hyperfines, which allows to estimate the
optical depth. However, we find that
line has hyperfines, which allows to estimate the
optical depth. However, we find that
![]() is optically thin in
almost all cases. In two sources with moderate optical depths, the
uncertainty in
is optically thin in
almost all cases. In two sources with moderate optical depths, the
uncertainty in ![]() is too large to derive meaningful constraints on the
column density. The line parameters are given in
Table 6 along with their column
densities. The column density is computed using the gas temperature
derived from
is too large to derive meaningful constraints on the
column density. The line parameters are given in
Table 6 along with their column
densities. The column density is computed using the gas temperature
derived from
![]() as the excitation temperature (see Appendix A).
as the excitation temperature (see Appendix A).
The derived
![]() abundances are a factor of 2-12 lower than the canonical value of
abundances are a factor of 2-12 lower than the canonical value of
![]() (Frerking et al. 1982). Wu & Yang (2005) find similar depletion factors for
the infrared dark cloud G79.2+0.38, another of the clumps in the cloud in the present study.
(Frerking et al. 1982). Wu & Yang (2005) find similar depletion factors for
the infrared dark cloud G79.2+0.38, another of the clumps in the cloud in the present study.
As mentioned in Sect. 2.4, the CO column density as determined from
![]() transitions might be underestimated if
transitions might be underestimated if
![]() is optically thick. However, the rarer isotopomer
is optically thick. However, the rarer isotopomer
![]() is expected to be optically thin. The canonical value of the relative abundance of
is expected to be optically thin. The canonical value of the relative abundance of
![]() w.r.t
w.r.t
![]() ,
A(18,17), is 3.65 (Wilson & Rood 1994) in the ISM. As discussed in Kramer et al. (1999), the measured ratios of the integrated intensities of the
,
A(18,17), is 3.65 (Wilson & Rood 1994) in the ISM. As discussed in Kramer et al. (1999), the measured ratios of the integrated intensities of the
![]() and
and
![]() lines can then be used to determine the
lines can then be used to determine the
![]() optical depth.
optical depth.
Due to the limited observing time, we observed the
![]() line only in the two brightest
line only in the two brightest
![]() sources. If R18,17 and
sources. If R18,17 and
![]() denotes the ratio of the integrated intensities of the
denotes the ratio of the integrated intensities of the
![]() and
and
![]() lines and the optical depth of
lines and the optical depth of
![]() as derived from the ratio, then
as derived from the ratio, then
For G35.19-1.73, we find that
![]() ,
which implies
that the correction factor for the column density given by
,
which implies
that the correction factor for the column density given by
![]() ,
is clearly smaller than the observed
depletion. However, for G81.74+0.59, the ratio itself
,
is clearly smaller than the observed
depletion. However, for G81.74+0.59, the ratio itself
![]() ,
suggesting that Eq. (3) is not valid anymore. It
is unlikely to be due to different excitation conditions or the extent of
emission of
,
suggesting that Eq. (3) is not valid anymore. It
is unlikely to be due to different excitation conditions or the extent of
emission of
![]() and
and
![]() .
It is indeed possible that there are real variations in
the ratio of
.
It is indeed possible that there are real variations in
the ratio of
![]() to
to
![]() ,
a possibility which needs to be investigated.
Additionally, the observed relatively small observed
peak brightness temperatures for
,
a possibility which needs to be investigated.
Additionally, the observed relatively small observed
peak brightness temperatures for
![]() exclude high optical depth in this line.
Therefore, to the extent that we assume G35.19-1.73 to be representative of our
sample, we may conclude that
exclude high optical depth in this line.
Therefore, to the extent that we assume G35.19-1.73 to be representative of our
sample, we may conclude that
![]() optically depth is "moderate''.
optically depth is "moderate''.
How do we account for the high deuteration we observe in these
pre/protostellar clumps? There are two main pathways to bring about
deuteration (Rodgers & Charnley 2001; Millar 2002, 2003; Roueff et al. 2005); a) gas-phase reactions, b) production of
deuterium bearing molecules on grain surfaces. Accretion of
neutrals onto the dust grains that would otherwise destroy
![]() enhances deuteration. Up to now all these processes have been used
to explain fractionation in different sources.
enhances deuteration. Up to now all these processes have been used
to explain fractionation in different sources.
In pre/protostellar cores, ion-molecule exchange reactions prevalent at low temperatures coupled with the depletion of CO from gas phase is preferred over grain production of highly deuterated species at temperatures of 20 K (Shah & Wootten 2001; Caselli et al. 2003).
The freeze-out of molecules from the gas onto the dust grains, particularly that of heavy molecules like CO in the cold initial phase has been predicted by chemical models
(Flower et al. 2005; Rodgers & Charnley 2001; Roberts & Millar 2000a,b; Brown & Millar 1989b; Watson 1976). These predictions have been validated by observations of molecular freeze out onto dust grains in low-mass starless dense cores (Caselli et al. 1999; Tafalla et al. 2002). The primary fractionation reaction that dominates at low temperatures (<20 K) is
Table 5:
![]() (J=2-1) line parameters.
(J=2-1) line parameters.
Table 6:
![]() and
and
![]() line parameters and column density.
line parameters and column density.
Roberts & Millar (2000b) show that at 10 K, accretion of neutrals onto the dust grains,
especially CO, leads to the formation of doubly deuterated molecules
such as ![]() and
and
![]() .
Based on these arguments,
we expect to see a correlation between deuteration and CO depletion.
In Fig. 3, we compare the
.
Based on these arguments,
we expect to see a correlation between deuteration and CO depletion.
In Fig. 3, we compare the
![]() fractionation and the
degree of CO depletion (depletion factor). As seen from the
correlation plot, there is a large scatter in the values and we do not
see any obvious trend of high depletion and deuteration.
Nevertheless, the main result is that we find very high deuterium
fractionation and CO depletion.
fractionation and the
degree of CO depletion (depletion factor). As seen from the
correlation plot, there is a large scatter in the values and we do not
see any obvious trend of high depletion and deuteration.
Nevertheless, the main result is that we find very high deuterium
fractionation and CO depletion.
![\begin{figure}
\par\includegraphics[angle=-90,width=9cm,clip]{5682fig3.eps} \end{figure}](/articles/aa/full/2007/19/aa5682-06/Timg76.gif) |
Figure 3:
Comparison of
|
| Open with DEXTER | |
Depletion could well occur on scales much smaller than the beam for
sources at the distances typical for these sources (several kpc). In
that case, the CO depletion that is measured as an average over the telescope beam is an underestimate of the true
depletion. The
![]() emission, on the other hand, is probably
dominated by the dense clumps. This could explain why the CO
depletion does not appear to track the deuteration in
Fig. 3. The uncertainties on the CO depletion factors are
quite large, mainly due to the uncertainty in the
emission, on the other hand, is probably
dominated by the dense clumps. This could explain why the CO
depletion does not appear to track the deuteration in
Fig. 3. The uncertainties on the CO depletion factors are
quite large, mainly due to the uncertainty in the ![]() column
density estimate from the 850
column
density estimate from the 850 ![]() m dust continuum. The largest
uncertainty is a factor of 4 in the dust opacity at 850
m dust continuum. The largest
uncertainty is a factor of 4 in the dust opacity at 850 ![]() m (Ossenkopf & Henning 1994; Krügel & Siebenmorgen 1994; Draine & Lee 1984). But we note that with the choice of the
Ossenkopf & Henning opacities, the derived column densities are
already lower than for e.g. Savage & Mathis (1979) dust properties. The
two studies other than ours that directly compare CO depletion and
deuterium fraction are by Bacmann et al. (2003) and
Crapsi et al. (2005). Bacmann et al. use the
m (Ossenkopf & Henning 1994; Krügel & Siebenmorgen 1994; Draine & Lee 1984). But we note that with the choice of the
Ossenkopf & Henning opacities, the derived column densities are
already lower than for e.g. Savage & Mathis (1979) dust properties. The
two studies other than ours that directly compare CO depletion and
deuterium fraction are by Bacmann et al. (2003) and
Crapsi et al. (2005). Bacmann et al. use the
![]() to
to
![]() ratios to determine the deuteration. They claim to
find a correlation between
ratios to determine the deuteration. They claim to
find a correlation between
![]() to
to
![]() ratios and
depletion and argue that the presence of a significant amount of O
(which is also an important
ratios and
depletion and argue that the presence of a significant amount of O
(which is also an important
![]() destroyer) in the gas phase
still undepleted might be responsible for the large scatter
observed. Crapsi et al. observe N2H+ and N2D+ toward 31
low-mass starless cores and find a good correlation between deuterium
fractionation and CO depletion.
destroyer) in the gas phase
still undepleted might be responsible for the large scatter
observed. Crapsi et al. observe N2H+ and N2D+ toward 31
low-mass starless cores and find a good correlation between deuterium
fractionation and CO depletion.
If ![]() is the fractional abundance of species X relative to
is the fractional abundance of species X relative to ![]() and
and
![]() is the abundance ratio of
is the abundance ratio of ![]() relative to
relative to ![]() ,
then under the assumption of steady-state and equating formation and destruction in
Eq. (4), one finds (Millar 2003)
,
then under the assumption of steady-state and equating formation and destruction in
Eq. (4), one finds (Millar 2003)
At low temperatures (T < 20 K) observed in cold cores, the
primary fractionation reaction is dominated by the forward reaction
in Eq. (4). At higher temperatures, the reverse reaction
becomes important in removing
![]() very rapidly from the
gas phase. Consequently, the decrease in primary fractionation
produces a corresponding decrease in secondary fractionation reactions
responsible for deuterium enhancements in molecules. Therefore, one naively
expects to find an anti-correlation between temperature and deuterium
fractionation. In Fig. 4, we plot the
very rapidly from the
gas phase. Consequently, the decrease in primary fractionation
produces a corresponding decrease in secondary fractionation reactions
responsible for deuterium enhancements in molecules. Therefore, one naively
expects to find an anti-correlation between temperature and deuterium
fractionation. In Fig. 4, we plot the
![]() fractionation
against the temperature for the high mass candidate pre/protostellar clumps (this paper) and
for pre/protostellar clumps in the lower mass regime from the literature.
The latest gas-phase predictions for [
fractionation
against the temperature for the high mass candidate pre/protostellar clumps (this paper) and
for pre/protostellar clumps in the lower mass regime from the literature.
The latest gas-phase predictions for [
![]() ]/[
]/[
![]() ]
(Roueff et al. 2005) are also plotted. This model assumes a density
of
]
(Roueff et al. 2005) are also plotted. This model assumes a density
of
![]()
![]() ,
carbon and oxygen depletion factors
of 5 and 15 respectively while Nitrogen is kept constant. Our data points nicely
fill in the missing observed data points between 10-20 K. Clearly the agreement with the model is moderate.
,
carbon and oxygen depletion factors
of 5 and 15 respectively while Nitrogen is kept constant. Our data points nicely
fill in the missing observed data points between 10-20 K. Clearly the agreement with the model is moderate.
![\begin{figure}
\par\includegraphics[angle=-90,width=8.8cm,clip]{5682fig4.eps} \end{figure}](/articles/aa/full/2007/19/aa5682-06/Timg93.gif) |
Figure 4:
Plot of
|
| Open with DEXTER | |
The levels of deuteration do fall off rapidly with increasing
temperature above 25 K (Roueff et al. 2005), but at the low
temperatures shown here the dependence is small. The Roueff et
al. models employ fixed H2 densities of around 105
![]() ,
which
would be typical averages over the 40
,
which
would be typical averages over the 40
![]() beam for our sources.
However the
beam for our sources.
However the
![]() emission will be enhanced at the peaks, where
higher densities and higher depletion would be expected to produce
higher levels of deuteration. Depletion, which increases over time
roughly with the increase in density, has a strong influence on
deuteration. The final levels of depletion and deuteration depend on
the accretion history (e.g. Flower et al. 2005), but it is
clear that higher densities or longer timescales result in higher
levels of both, e.g. Roberts et al. (2003) derive
[
emission will be enhanced at the peaks, where
higher densities and higher depletion would be expected to produce
higher levels of deuteration. Depletion, which increases over time
roughly with the increase in density, has a strong influence on
deuteration. The final levels of depletion and deuteration depend on
the accretion history (e.g. Flower et al. 2005), but it is
clear that higher densities or longer timescales result in higher
levels of both, e.g. Roberts et al. (2003) derive
[
![]() ]/[
]/[
![]() ]
ratios of 0.4-0.8 for densities of
]
ratios of 0.4-0.8 for densities of
![]()
![]() .
.
However, most of the low [
![]() ]/[
]/[
![]() ]
ratios and interestingly the
high temperatures are from the sources where
]
ratios and interestingly the
high temperatures are from the sources where
![]() column densities were estimated from the integrated intensity of the line and therefore are really lower limits on the [
column densities were estimated from the integrated intensity of the line and therefore are really lower limits on the [
![]() ]/[
]/[
![]() ]
ratios. The exact temperature which we measure for a clump of course depends on the combination of hot/cold gas in the beam, which can explain the scatter between 15-18 K where in some cases we are still seeing a lot of deuteration and in others it has already diminished.
]
ratios. The exact temperature which we measure for a clump of course depends on the combination of hot/cold gas in the beam, which can explain the scatter between 15-18 K where in some cases we are still seeing a lot of deuteration and in others it has already diminished.
On average, the fractionation observed in sources in our sample is very high. However, note that few sources at temperatures above 15 K show an order of magnitude lower deuteration than the model predictions, while others show extremely high deuterations, much higher than those found in low mass pre/protostellar cores.
There could be three main reasons for the very low fractionation
estimated for a few sources. First, one of the main assumption in
deriving the [
![]() ]/[
]/[
![]() ]
ratio is that the filling factors for both
molecular transitions are the same. Any deviation from this
assumption might result in a discrepant ratio. Second, these sources
might be relatively more evolved. In such a case, the kinetic
temperatures derived from the
]
ratio is that the filling factors for both
molecular transitions are the same. Any deviation from this
assumption might result in a discrepant ratio. Second, these sources
might be relatively more evolved. In such a case, the kinetic
temperatures derived from the
![]() (1, 1) and (2, 2) lines might only
be a lower limit. In such cases where the gas temperature is
roughly higher than 20 K, the rotational temperature does not
represent the real gas temperature. Hence the column density
(deuteration) determined may be under estimated. Third, the sources could be chemically young, hence
the timescale to reach the high deuteration in these sources is larger
than their age. Tafalla & Santiago (2004) recently discussed such a chemically young low mass core. It is also possible that
(1, 1) and (2, 2) lines might only
be a lower limit. In such cases where the gas temperature is
roughly higher than 20 K, the rotational temperature does not
represent the real gas temperature. Hence the column density
(deuteration) determined may be under estimated. Third, the sources could be chemically young, hence
the timescale to reach the high deuteration in these sources is larger
than their age. Tafalla & Santiago (2004) recently discussed such a chemically young low mass core. It is also possible that
![]() might be tracing different regions from
might be tracing different regions from
![]() and that the temperature derived from
and that the temperature derived from
![]() may not be the temperature of
may not be the temperature of
![]() .
.
A simple model for grain surface formation of multiply deuterated
molecules is considered by Brown & Millar (1989a) and predicts the
abundances of deuterated species, in order to differentiate between
the gas and grain chemistry. According to the Brown and Millar model prediction, the
abundances of deuterated species scale as [
![]() ]/[
]/[
![]() ]
]
![]()
![]() for grain surface formation.
for grain surface formation.
Alternatively, Roberts & Millar (2000a) propose a gas-phase chemistry where the effects of the freeze out of gas phase species onto grains is included and find an enhancement in the fractionation of both singly and doubly deuterated species.
Very deep observations of the
![]() 110-101 line for two
sources G35.19-1.73 and G81.74+0.59, did not result in any detection at an rms
of
110-101 line for two
sources G35.19-1.73 and G81.74+0.59, did not result in any detection at an rms
of ![]() 20 mK. Based on the 3
20 mK. Based on the 3![]() upper limits, we then derive
[
upper limits, we then derive
[
![]() ]/[
]/[
![]() ]
(see Appendix A) and find that
]
(see Appendix A) and find that
![\begin{displaymath}{\rm\Big({\frac{1}{3} ([{\rm NH_{2}D]/[NH_3]})^2\Big)}_{observed}<(0.06)_{G35.19}; (0.04)_{G81.74}}
\end{displaymath}](/articles/aa/full/2007/19/aa5682-06/img98.gif)
How do the obtained upper limits compare with the predictions of
recent gas-phase deuterium chemistry models? In Fig. 5,
we compare the results of model calculations with our observed upper
limits for the ratio of
![]() to
to
![]() (Roueff et al. 2005). We
have used their "model 2'' which gives the highest molecular
fractional abundances for the N-bearing species. In this context it is
also interesting to note that while Roueff et al. find that their
model underpredicts the
(Roueff et al. 2005). We
have used their "model 2'' which gives the highest molecular
fractional abundances for the N-bearing species. In this context it is
also interesting to note that while Roueff et al. find that their
model underpredicts the
![]() to
to
![]() ratio in low mass prestellar
cores (LDN 134N, LDN 1689N, Barnard 1, LDN 1544), it agrees well with
the observed ratio in our sample.
ratio in low mass prestellar
cores (LDN 134N, LDN 1689N, Barnard 1, LDN 1544), it agrees well with
the observed ratio in our sample.
![\begin{figure}
\par\includegraphics[height=8.8cm,angle=-90]{5682fig5.eps} \end{figure}](/articles/aa/full/2007/19/aa5682-06/Timg100.gif) |
Figure 5: Comparison of obtained upper limits for G35.19-1.73 and G81.74+0.59 with the gas phase model predictions (Roueff et al. 2005, their model 2). |
| Open with DEXTER | |
Hence, we cannot reject active grain or gas-phase chemistry on the
basis of the observed
![]() upper limits. While a gas-phase model
along with condensation of neutral species onto grain mantles
adequately explains moderate deuteration (
upper limits. While a gas-phase model
along with condensation of neutral species onto grain mantles
adequately explains moderate deuteration (
![]() /
/
![]() )
observed towards
some sources, the very high fractionation we derive remains
unexplained. Although we do not understand the grain-surface
chemistry, particularly in this case involving deuterated ammonia, a
naive extrapolation from the surface-chemistry involving H, D, C and O
and a high grain-surface D/H ratio might explain the significant
enhancement of deuterated ammonia (Caselli et al. 2004).
However, the efficacy of this model is strongly dependent on the
gas-phase atomic D/H ratio, which in the extreme case of our sample
implies an enhancement of
)
observed towards
some sources, the very high fractionation we derive remains
unexplained. Although we do not understand the grain-surface
chemistry, particularly in this case involving deuterated ammonia, a
naive extrapolation from the surface-chemistry involving H, D, C and O
and a high grain-surface D/H ratio might explain the significant
enhancement of deuterated ammonia (Caselli et al. 2004).
However, the efficacy of this model is strongly dependent on the
gas-phase atomic D/H ratio, which in the extreme case of our sample
implies an enhancement of ![]() 104 over the cosmic D/H ratio.
104 over the cosmic D/H ratio.
Although the exact evolutionary status of the sources
(i.e. pre/protostellar) in our sample cannot be determined with
certainty, there are several observational evidences that substantiate
their high mass pre/protostellar nature. The large line broadening (
![]()
![]() )
observed in all molecular tracers, together with the high
H2 column density (
)
observed in all molecular tracers, together with the high
H2 column density (
![]() cm-2) is
characteristic of massive star forming regions. These sources have masses
between a few hundred to a few thousand solar masses. Their
source-averaged H2 densities are a few 105
cm-2) is
characteristic of massive star forming regions. These sources have masses
between a few hundred to a few thousand solar masses. Their
source-averaged H2 densities are a few 105
![]() - unlikely for
low-mass objects. Moreover, the physical properties of these cores
are similar to those associated with UCH II regions
(e.g. Thompson et al. 2006). Therefore we expect them
to be forming (or on the verge of forming) high-mass stars. The exact
nature of these sources will be discussed in a future paper (Hatchell
et al. in prep.).
- unlikely for
low-mass objects. Moreover, the physical properties of these cores
are similar to those associated with UCH II regions
(e.g. Thompson et al. 2006). Therefore we expect them
to be forming (or on the verge of forming) high-mass stars. The exact
nature of these sources will be discussed in a future paper (Hatchell
et al. in prep.).
The deuteration of a few tens of percent in ammonia is comparable to
the highest which have been measured in the interstellar medium, which
occur in low-mass prestellar cores. The related ratio
[N2D+]/[N2H+] exceeds 20% in a few prestellar cores
including L1544 (Crapsi et al. 2004). High deuterated ammonia abundances
have also been measured in early-stage protostars: the
[NH2D]/[NH3] ratio reaches over 30% in protostars in Perseus
(Hatchell 2003), and detections of triply deuterated ammonia
(van der Tak et al. 2002; Lis et al. 2002) and methanol (Parise et al. 2004) have all been in the
environments of protostars, though deuteration of ![]() 5%
is more common (Saito et al. 2000; Hatchell 2003; Shah & Wootten 2001). The high
deuteration of our sample supports the idea that these
are the high-mass equivalent of prestellar or protostellar cores.
5%
is more common (Saito et al. 2000; Hatchell 2003; Shah & Wootten 2001). The high
deuteration of our sample supports the idea that these
are the high-mass equivalent of prestellar or protostellar cores.
Hot molecular cores, believed to be the early protostellar stage of
high mass star formation and potentially a later evolutionary stage of
our sources, have a low molecular deuteration fractionation ![]() 10-3, consistent with ice formation at a higher temperature of
60-80 K and little gas-phase deuteration, as expected at high
temperatures (Hatchell et al. 1998; Roberts et al. 2002; Hatchell et al. 1999). High
[NH2D]/[NH3] ratios are observed in the Orion region but only in
the compact ridge and not the hot core (Turner 1990). If our
candidate precluster cores are precursors of hot cores, then the
chemistry must radically alter during the later evolution of the hot
core, perhaps with continuing accretion at higher temperatures during
the early protostellar phase dominating the ice production.
10-3, consistent with ice formation at a higher temperature of
60-80 K and little gas-phase deuteration, as expected at high
temperatures (Hatchell et al. 1998; Roberts et al. 2002; Hatchell et al. 1999). High
[NH2D]/[NH3] ratios are observed in the Orion region but only in
the compact ridge and not the hot core (Turner 1990). If our
candidate precluster cores are precursors of hot cores, then the
chemistry must radically alter during the later evolution of the hot
core, perhaps with continuing accretion at higher temperatures during
the early protostellar phase dominating the ice production.
Let us define the abundance ratio,
![]() , as
, as
The isotopomeric species of HCN,
![]() and
and
![]() have been often
observed in their J=1-0 transition toward various local molecular
clouds (Dahmen et al. 1995; Hirota et al. 1998; Ikeda et al. 2002) to estimate the ratio
have been often
observed in their J=1-0 transition toward various local molecular
clouds (Dahmen et al. 1995; Hirota et al. 1998; Ikeda et al. 2002) to estimate the ratio
![]() .
These lines can be
observed with the same receiver and hence the ratio derived will be
independent of calibration errors. Moreover, the optical depth can be
measured from the three hyperfine components of the
.
These lines can be
observed with the same receiver and hence the ratio derived will be
independent of calibration errors. Moreover, the optical depth can be
measured from the three hyperfine components of the
![]() line. As
mentioned in Sect. 2.5,
line. As
mentioned in Sect. 2.5,
![]() is optically thin in almost
all cases and hence the observed ratios must indicate the abundance
ratio
is optically thin in almost
all cases and hence the observed ratios must indicate the abundance
ratio
![]() ,
since the column density estimates are free from
bias due to photon trapping effects.
,
since the column density estimates are free from
bias due to photon trapping effects.
In Fig. 6 we plot the abundance ratio of
![]() and
and
![]() as a function of distance from the galactic centre for our sources.
The ratio of the abundances does not seem to correlate with the distance. However, the formal error bars are too large to be able to make any strong argument against a correlation of
as a function of distance from the galactic centre for our sources.
The ratio of the abundances does not seem to correlate with the distance. However, the formal error bars are too large to be able to make any strong argument against a correlation of
![]() with galactocentric distance.
with galactocentric distance.
![\begin{figure}
\par\includegraphics[height=8.7cm,angle=-90]{5682fig6.eps} \end{figure}](/articles/aa/full/2007/19/aa5682-06/Timg105.gif) |
Figure 6:
|
| Open with DEXTER | |
If we adopt the canonical values for the
![]() of 77
and
of 77
and
![]() of 450 toward the local interstellar medium
(ISM), then the implied
of 450 toward the local interstellar medium
(ISM), then the implied
![]() to
to
![]() abundance ratio is
abundance ratio is
![]() 6 (Wilson & Rood 1994, their Table 4). From our data, we
find that most of the values tend to be higher, consistent with a mean
value of 17. This ratio is intermediate between that found toward the
galactic centre (
6 (Wilson & Rood 1994, their Table 4). From our data, we
find that most of the values tend to be higher, consistent with a mean
value of 17. This ratio is intermediate between that found toward the
galactic centre (![]() 30), an extreme high mass star-forming region
and the local ISM (
30), an extreme high mass star-forming region
and the local ISM (![]() 6) where typically low mass star formation
pervades (see again Table 4 of Wilson & Rood 1994).
6) where typically low mass star formation
pervades (see again Table 4 of Wilson & Rood 1994).
The SCAMPS sources are in the close
vicinity of massive star forming regions and hence the energetic UV
radiation could cause a isotope-selective photo-destruction
(Schilke et al. 1992). Chemical fractionation is also likely to
play an important role in the observed high values. The high
deuterium fractionation we observed must be equally affecting the
abundances of
![]() and
and
![]() .
Therefore, if at all, chemical
fractionation were to play a role, it must be attributed to an
anomalous fractionation in the isotopes of either N or C. A high
ratio implies either a low
.
Therefore, if at all, chemical
fractionation were to play a role, it must be attributed to an
anomalous fractionation in the isotopes of either N or C. A high
ratio implies either a low
![]() fractionation or
fractionation or
![]() fractionation in HCN. As noted earlier in this section, the carbon
isotopic ratio is known to vary across the Galaxy
(Wilson & Rood 1994). The ratio is influenced mainly by a)
the self-shielding property of CO, b)
fractionation in HCN. As noted earlier in this section, the carbon
isotopic ratio is known to vary across the Galaxy
(Wilson & Rood 1994). The ratio is influenced mainly by a)
the self-shielding property of CO, b)
![]() selective isotopic
fractionation, and c) stellar winds from stars more massive than the sun,
which favours the production of
selective isotopic
fractionation, and c) stellar winds from stars more massive than the sun,
which favours the production of
![]() over
over
![]() (Krügel 2003). The deviation from the canonical value in the
local ISM could be therefore due to a complex chemistry or
environment in these high-mass star forming regions.
(Krügel 2003). The deviation from the canonical value in the
local ISM could be therefore due to a complex chemistry or
environment in these high-mass star forming regions.
Although the number of assumptions involved is considerable, in particular that the two species may not be exactly tracing the same volume of gas as evidenced by the differences in their line widths, the ratio we derive clearly indicates the differences in the properties of high mass and low mass star forming regions.
In this paper, we report the study of physical and chemical properties
of a new sample of high-mass pre/protocluster clumps. We have observed
32 sources in the
![]() (1, 1) and (2, 2),
(1, 1) and (2, 2),
![]() (111-101),
(111-101),
![]() (J=1-0 and 2-1),
(J=1-0 and 2-1),
![]() and
and
![]() (J=1-0) transitions. We have
clear detections of
(J=1-0) transitions. We have
clear detections of
![]() in 22 sources and 100% detection in
in 22 sources and 100% detection in
![]() .
.
Our observations suggest large deuterium enhancements (up to 66%),
the largest reported so far. We also derived the amount of molecular
depletion by comparing the
![]() column density with the
column density with the ![]() column density derived from dust continuum observations, and we find that
the degree of CO depletion is a factor 2-12 higher compared to the
canonical value for its abundance. The derived abundance ratio of
column density derived from dust continuum observations, and we find that
the degree of CO depletion is a factor 2-12 higher compared to the
canonical value for its abundance. The derived abundance ratio of
![]() to
to
![]() is indicative of a very high
is indicative of a very high
![]() /
/
![]() ratio, discrepant from that found toward the local ISM. These
properties clearly reflect the complex chemistry in regions of high
mass star formation.
ratio, discrepant from that found toward the local ISM. These
properties clearly reflect the complex chemistry in regions of high
mass star formation.
This study shows that depletion and high deuteration exist towards
massive cold cores in massive star forming regions and makes
them promising candidates for the early phases of massive star
formation. In a subsequent paper, we will discuss the spatial distribution of
![]() in two sources
observed with high angular resolution, confirming the high deuteration
found from this study.
in two sources
observed with high angular resolution, confirming the high deuteration
found from this study.
Acknowledgements
T. Pillai was supported for this research through a stipend from the International Max Planck Research School (IMPRS) for Radio and Infrared Astronomy at the University of Bonn. JH was supported at MPIfR Bonn by DFG SFB 494 and holds a PPARC AF at Exeter.
We used the following expressions to determine the column density of the different molecules.
The column density is given by,
Here,
![]() is defined as
is defined as
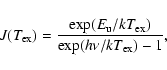 |
(A.2) |
In the optically thin case,
The
![]() partition function is determined by considering the contribution of the different energy levels from J=0 to J=2, while the metastable levels from (J,K=1,1) to (J,K=3,3) have been considered for
partition function is determined by considering the contribution of the different energy levels from J=0 to J=2, while the metastable levels from (J,K=1,1) to (J,K=3,3) have been considered for
![]() .
.
For other molecular species, the partition function
![]() at temperature
at temperature
![]() is
estimated as
is
estimated as
![]() ,
where
,
where ![]() and
and ![]() are the best fit parameters from a fit to the partition function obtained from JPL catalogue at different excitation
temperatures from 10-300 K.
are the best fit parameters from a fit to the partition function obtained from JPL catalogue at different excitation
temperatures from 10-300 K.
In Table A.1, we give the dipole moments we used for different molecules and the partition function,
![]() at temperature
at temperature
![]() K.
K.
By fitting the main and the hyperfine components of the (1, 1) line
and the main component of the (2, 2) line, we obtain the rotational
temperature. The kinetic temperature and
![]() column density, have
been derived using the standard formulation for
column density, have
been derived using the standard formulation for
![]() spectra
(Bachiller et al. 1987). The
spectra
(Bachiller et al. 1987). The
![]() column density has been
estimated assuming that the level populations are thermalised,
i.e.,
column density has been
estimated assuming that the level populations are thermalised,
i.e.,
![]() .
A similar assumption holds for our
estimation of
.
A similar assumption holds for our
estimation of
![]() column densities.
column densities.
The upper limit on the
![]() column density is estimated from the
integrated intensity. This quantity was measured by integrating over a
velocity range determined from the
column density is estimated from the
integrated intensity. This quantity was measured by integrating over a
velocity range determined from the
![]() line width around the LSR
velocity of the source. The 1
line width around the LSR
velocity of the source. The 1![]() uncertainty on this value is
estimated from the rms of the noise in the channels where no line
emission is expected, and, is given by
uncertainty on this value is
estimated from the rms of the noise in the channels where no line
emission is expected, and, is given by
![]() .
.
Table A.1:
Molecular parameters used to estimate
![]() .
.
Table A.2:
![]() line parameters with uncertainties (in brackets) from the hyperfine/Gaussian fits.
line parameters with uncertainties (in brackets) from the hyperfine/Gaussian fits.
Table A.3:
![]() line parameters with uncertainties (in brackets) from the hyperfine/Gaussian fits.
line parameters with uncertainties (in brackets) from the hyperfine/Gaussian fits.
![\begin{figure}
\par\includegraphics[height=17cm]{5682fig8.eps} \end{figure}](/articles/aa/full/2007/19/aa5682-06/Timg134.gif) |
Figure A.2:
Lower spectrum: 30 m
|
Table A.4:
![]() (J=1-0) and (J=2-1) line parameters.
(J=1-0) and (J=2-1) line parameters.