A&A 454, 863-881 (2006)
DOI: 10.1051/0004-6361:20054199
A. H. Córsico1,2,![]() -
L. G. Althaus1,2,
-
L. G. Althaus1,2,![]()
1 - Facultad de Ciencias Astronómicas y Geofísicas,
Universidad Nacional de La Plata, Paseo del Bosque s/n, (1900) La Plata, Argentina
2 - Instituto de Astrofísica La Plata, IALP,
CONICET, Argentina
Received 13 September 2005 / Accepted 26 March 2006
Abstract
An adiabatic, nonradial pulsation study of GW Vir stars
is presented. The pulsation calculations were based on PG 1159
evolutionary sequences with different stellar masses artificially
derived from a full
evolutionary sequence of 0.5895 ![]() that has been computed by taking
the evolutionary history of the progenitor star into account. The artificial
sequences were constructed by appropriately scaling
the stellar mass of the 0.5895-
that has been computed by taking
the evolutionary history of the progenitor star into account. The artificial
sequences were constructed by appropriately scaling
the stellar mass of the 0.5895-![]() sequence well before the models
reached the low-luminosity, high-gravity stage of the GW Vir domain.
We computed g-mode pulsation periods appropriate to GW Vir variable
stars. The implications for the mode-trapping properties of our PG
1159 models are discussed at length. We found that the mode-trapping
features characterizing our PG 1159 models are mostly fixed by the
stepped shape of the core chemical profile left by prior convective
overshooting. This is particularly true at least for the range of
periods observed in GW Vir stars. In addition, we make asteroseismic
inferences about the internal structure of the GW Vir stars PG 1159-035,
PG 2131+066, PG 1707+427, and PG 0122+200.
sequence well before the models
reached the low-luminosity, high-gravity stage of the GW Vir domain.
We computed g-mode pulsation periods appropriate to GW Vir variable
stars. The implications for the mode-trapping properties of our PG
1159 models are discussed at length. We found that the mode-trapping
features characterizing our PG 1159 models are mostly fixed by the
stepped shape of the core chemical profile left by prior convective
overshooting. This is particularly true at least for the range of
periods observed in GW Vir stars. In addition, we make asteroseismic
inferences about the internal structure of the GW Vir stars PG 1159-035,
PG 2131+066, PG 1707+427, and PG 0122+200.
Key words: dense matter - stars: white dwarfs - stars: oscillations
GW Vir (or DOV) stars currently constitute one of the most exciting
classes of variable stars, since they represent an evolutionary
connection between the cool, very luminous, asymptotic giant branch
(AGB) stars and the hot, extremely compact white dwarf (WD) stars.
Since the discovery of their prototype, PG 1159-035, by McGraw et al. (1979), GW Vir stars have been the focus of numerous observational
and theoretical efforts. These stars are believed to be the variable
members of the PG 1159 family, a spectral class of stars characterized
by a rather abnormal surface chemical composition, with atmospheres
devoid of hydrogen and, instead, rich in helium (
![]() ), carbon (
), carbon (
![]() ), and oxygen (
), and oxygen (
![]() )
(Werner et al. 1997). The
PG 1159 stars (
)
(Werner et al. 1997). The
PG 1159 stars (
![]() K and
K and
![]() )
are thought to be
the descendants of post-AGB stars that, after experiencing a late
thermal pulse at the beginning of the WD cooling track, return to AGB,
and finally evolve into the hot central stars of planetary nebulae as
hydrogen-deficient pre-WD stars - the so-called "born-again''
scenario (Fujimoto 1977; Schönberner 1979; Iben et al. 1983). In
fact, recent evolutionary calculations of the born-again scenario
incorporating convective overshooting have been successful in
reproducing the observed photospheric composition of PG 1159 stars
(Herwig et al. 1999; Althaus et al. 2005).
)
are thought to be
the descendants of post-AGB stars that, after experiencing a late
thermal pulse at the beginning of the WD cooling track, return to AGB,
and finally evolve into the hot central stars of planetary nebulae as
hydrogen-deficient pre-WD stars - the so-called "born-again''
scenario (Fujimoto 1977; Schönberner 1979; Iben et al. 1983). In
fact, recent evolutionary calculations of the born-again scenario
incorporating convective overshooting have been successful in
reproducing the observed photospheric composition of PG 1159 stars
(Herwig et al. 1999; Althaus et al. 2005).
![\begin{figure}
\par\includegraphics[width=12.6cm,clip]{4199f-01.eps}
\end{figure}](/articles/aa/full/2006/30/aa4199-05/Timg51.gif) |
Figure 1:
The observed location of PG 1159 stars
in the
|
| Open with DEXTER | |
The GW Vir variables are low-amplitude, multiperiodic g-mode pulsators
with periods in the range of 5 to 30 min. Eleven such
variables are presently known, six of which are associated with a
planetary nebula and sometimes termed PNNV (Planetary Nebula Nuclei
Variable). The remainder objects that lack a surrounding nebulae are
called "naked'' GW Vir stars. In Fig. 1 we plot the
observed location of the known GW Vir stars in the
![]() plane. In addition, we have included in the figure some
non-variable PG 1159 stars, as well as PG 1159 stars for which
photometric data are not available. Note that GW Vir stars are
separated into two subgroups, one containing low-gravity,
high-luminosity stars - the PNNVs RX J2117+3412, HE 1429-1209, K1-16,
NGC 246, HS 2324+3944, Lo 4, and Abell 43 - and the other
corresponding to high-gravity stars - the naked GW Vir stars PG 1159-035, PG 2131+066,
PG 1707+427, and PG 0122+200. Finally,
among the low-gravity GW Vir stars there are two objects labeled
as pulsating "hybrid-PG 1159'' - HS 2324+3944 and Abell 43. They
are variable PG 1159 stars showing strong Balmer lines of hydrogen in
their spectra.
plane. In addition, we have included in the figure some
non-variable PG 1159 stars, as well as PG 1159 stars for which
photometric data are not available. Note that GW Vir stars are
separated into two subgroups, one containing low-gravity,
high-luminosity stars - the PNNVs RX J2117+3412, HE 1429-1209, K1-16,
NGC 246, HS 2324+3944, Lo 4, and Abell 43 - and the other
corresponding to high-gravity stars - the naked GW Vir stars PG 1159-035, PG 2131+066,
PG 1707+427, and PG 0122+200. Finally,
among the low-gravity GW Vir stars there are two objects labeled
as pulsating "hybrid-PG 1159'' - HS 2324+3944 and Abell 43. They
are variable PG 1159 stars showing strong Balmer lines of hydrogen in
their spectra.
A longstanding problem associated with GW Vir stars is related to the
excitation mechanism for the pulsations and, in particular, to the
chemical composition of the driving zone, an issue that has always
attracted the attention of theorists but that until very recently
has eluded all attempts at understanding. In their pioneering
works, Starrfield et al. (1983, 1984, 1985) and Stanghellini et al. (1991) realized that g-mode pulsations with periods around 500 s
could be driven in PG 1159 models by the
![]() -mechanism associated
with the partial ionization of carbon and oxygen. While these authors
were successful in finding the correct destabilizing mechanism, the
periods of the excited modes were too short compared to the
observed periodicities in GW Vir stars. In addition, their models
required a driving region very poor in helium needed to excite pulsations.
-mechanism associated
with the partial ionization of carbon and oxygen. While these authors
were successful in finding the correct destabilizing mechanism, the
periods of the excited modes were too short compared to the
observed periodicities in GW Vir stars. In addition, their models
required a driving region very poor in helium needed to excite pulsations.
This requirement led to the suspicion that a composition gradient might exist to make the helium-devoid envelope and the helium-rich atmospheric layers compatible. Even very recent theoretical work by Bradley & Dziembowski (1996) and Cox (2003) points out the necessity of a different chemical composition in the driving region from the observed surface composition. This is difficult to explain in view of the fact that PG 1159 stars are still experiencing mass loss, thereby preventing any gravitational settling of carbon and oxygen. Clearly at odds with the conclusions of these works, the calculations by Saio (1996) and Gautschy (1997), and more recently by Quirion et al. (2004) and Gautschy et al. (2005), demonstrate that g-mode pulsations in the range of periods of GW Vir stars could be easily driven in PG 1159 models at satisfactory effective temperatures, with a uniform envelope composition that is compatible with the observed photospheric abundances.
While non-adiabatic stability issues like those mentioned above are of the utmost importance in elucidating the cause of GW Vir pulsations and in placing constraints on the composition of the subphotospheric layers, there is another avenue that may help to extract valuable information about the internal structure and evolutionary status of PG 1159 stars: considering adiabatic pulsation periods alone. This approach, known as asteroseismology, allows us to derive structural parameters for individual pulsators by matching adiabatic periods with the observed periodicities. Current examples of the asteroseismic studies of GW Vir stars are those of Kawaler & Bradley (1994) (PG 1159-035), Kawaler et al. (1995) (PG 2131+066), O'Brien et al. (1998) (PG 0122+200), Vauclair et al. (2002) (RX J2117+341), and Kawaler et al. (2004) (PG 1707+427). These studies have been successful at providing precise mass determinations and valuable constraints on the outer compositional stratification of PG 1159 stars. As important as they were, these investigations were based on stellar models that were not actually fully self-consistent evolutionary PG 1159 models. With the notable exception of the exemplary work of Kawaler & Bradley (1994), all these studies use the observed mean period spacing and the asymptotic theory of stellar pulsations alone to make asteroseismic inferences; that is, no detailed period fitting was carried out in those works. In part, the reason for this is that, for most of GW Vir stars (with exception of PG 1159-035), the observed mode density does not appear to be high enough for detailed asteroseismic analysis.
It is important to mention that for applications requiring accurate values of the adiabatic pulsation periods of GW Vir stars only full evolutionary models can be used. This is particularly true for asteroseismic fits to individual stars. In fact, as has been shown, stellar models representing PG 1159 stars should reflect the thermal structure of their progenitors because that structure primarily determines the adiabatic period spectrum, at least in the high luminosity phases (Kawaler et al. 1985). This is of the utmost importance for the theoretically expected rates of the pulsation period change - see, e.g., Kawaler et al. (1986). In addition, special care must be taken in the numerical simulations of the evolutionary stages prior to the AGB phase. Specifically, the modeling process should include extra mixing episodes beyond the fully convective core during central helium burning (Straniero et al. 2003). Overshoot during the central helium burning stage leads to sharp variations in the chemical profile at the inner core - see Straniero et al. (2003) and Althaus et al. (2003). This, in turn, could have a strong impact on the mode-trapping properties of the PG 1159 models. Last, but not least, a self-consistent treatment of the post-AGB evolution is required. In fact, the details of the last helium thermal pulse on the early WD cooling branch and the subsequent born-again episode determine, to a great extent, the chemical stratification and composition of the outer layers of the hot PG 1159 stars. The composition stratification of the stellar envelope, in turn, plays an important role in the mode-trapping characteristics of PG 1159 stars - see Kawaler & Bradley (1994).
All these requirements are completely fulfilled by the
0.5895-![]() PG 1159 models presented recently by Althaus et al.
(2005). In fact, these authors have computed the evolution of
hydrogen-deficient post-AGB WDs taking into account a complete and
detailed treatment of the physical processes that lead to the
formation of such stars. These models have been recently used for
the non-adiabatic studies of GW Vir stars by Gautschy et al. (2005).
PG 1159 models presented recently by Althaus et al.
(2005). In fact, these authors have computed the evolution of
hydrogen-deficient post-AGB WDs taking into account a complete and
detailed treatment of the physical processes that lead to the
formation of such stars. These models have been recently used for
the non-adiabatic studies of GW Vir stars by Gautschy et al. (2005).
The aim of this paper is to explore the adiabatic pulsation properties of GW Vir stars by employing the full evolutionary PG 1159 models of Althaus et al. (2005). In addition, we employ these models to make seismic inferences about several GW Vir stars. The paper is organized as follows. In Sect. 2, we describe the main characteristics of our numerical codes and the PG 1159 models employed. The adiabatic pulsational properties for our PG 1159 sequences are described in detail in Sect. 3. Special emphasis is put on the mode-trapping properties of our models. Section 4 is devoted to describing the application of our extensive period computations for the asteroseismic inferences of the main structural properties of various high-gravity GW Vir stars. Finally, in Sect. 5 we briefly summarize our main findings and draw our conclusions.
We mention that during the thermally pulsing AGB phase, our models
experience appreciable third dredge-up, which causes the
carbon-oxygen ratio to increase from ![]() 0.25 to
0.25 to
![]() 0.34 by the time the remnant departs from the AGB.
Apart from implications for the chemical stratification of the
post-AGB remnant, the occurrence of the third dredge-up mixing event affects the degeneracy of the carbon-oxygen core, which in turn affects the location of the
PG 1159 tracks (see Werner & Herwig 2006, for comments).
After experiencing 10 thermal pulses, the progenitor departs from the AGB
and evolves toward high effective temperatures, where it experiences a
final thermal pulse during the early WD cooling phase - a very late
thermal pulse and the ensuing born-again episode, see Blöcker (2001)
for a review - where most of the residual hydrogen envelope is
burnt. After the occurrence of a double-loop in the
Hertzsprung-Russell diagram, the now hydrogen-deficient, quiescent
helium-burning 0.5895-
0.34 by the time the remnant departs from the AGB.
Apart from implications for the chemical stratification of the
post-AGB remnant, the occurrence of the third dredge-up mixing event affects the degeneracy of the carbon-oxygen core, which in turn affects the location of the
PG 1159 tracks (see Werner & Herwig 2006, for comments).
After experiencing 10 thermal pulses, the progenitor departs from the AGB
and evolves toward high effective temperatures, where it experiences a
final thermal pulse during the early WD cooling phase - a very late
thermal pulse and the ensuing born-again episode, see Blöcker (2001)
for a review - where most of the residual hydrogen envelope is
burnt. After the occurrence of a double-loop in the
Hertzsprung-Russell diagram, the now hydrogen-deficient, quiescent
helium-burning 0.5895-![]() remnant evolves at almost constant
luminosity to the domain of PG 1159 stars with a surface chemical
composition rich in helium, carbon and oxygen:
(4He,12C,16O) = (0.306, 0.376, 0.228)
remnant evolves at almost constant
luminosity to the domain of PG 1159 stars with a surface chemical
composition rich in helium, carbon and oxygen:
(4He,12C,16O) = (0.306, 0.376, 0.228)![]() . This is in good agreement with
the surface abundance patterns observed in pulsating PG 1159 stars
(Dreizler & Heber 1998; Werner 2001). Also, the surface nitrogen
abundance (about 0.01 by mass) predicted by our models is in line with
the one detected in pulsating PG 1159 stars (see Dreizler & Heber 1998).
. This is in good agreement with
the surface abundance patterns observed in pulsating PG 1159 stars
(Dreizler & Heber 1998; Werner 2001). Also, the surface nitrogen
abundance (about 0.01 by mass) predicted by our models is in line with
the one detected in pulsating PG 1159 stars (see Dreizler & Heber 1998).
We mention that the nuclear network considered in the stellar modelling accounts explicitly for 16 chemical elements and 34 thermonuclear reaction rates to describe hydrogen and helium burning. Abundance changes for the elements considered were included by means of a time-dependent scheme that simultaneously treats nuclear evolution and mixing processes due to convection and overshooting. A treatment of this kind is particularly necessary during the extremely short-lived phase of the born-again episode, for which the assumption of instantaneous mixing is inadequate. In particular, overshooting is treated as a diffusion process (see, e.g., Herwig et al. 1997) and has been considered during all evolutionary phases. Radiative opacities are those of OPAL (including carbon- and oxygen-rich compositions; Iglesias & Rogers 1996), complemented at low temperatures with the molecular opacities from Alexander & Ferguson (1994).
Because of the considerable load of computing time and the numerical
difficulty involved in the generation of PG 1159 stellar models
that take the complete evolutionary history of the
progenitor star into account, we were forced to consider one case for the complete evolution, that is, the 0.5895-![]() sequence. However, to reach a
deeper understanding of the various trends exhibited by pulsations in
GW Vir stars, assessing the dependence of the pulsation
properties of PG 1159 models on the several structural
parameters
should be highly desirable. This statement is particularly true
for the stellar mass of the models. We consider a
set of additional sequences of models within a narrow range of stellar
masses. In the absence of actual self-consistent evolutionary computations
for post-born-again PG 1159 models with different stellar masses, we
elect to create several evolutionary sequences by employing an
artificial procedure starting from our "seed'' model sequence of
0.5895
sequence. However, to reach a
deeper understanding of the various trends exhibited by pulsations in
GW Vir stars, assessing the dependence of the pulsation
properties of PG 1159 models on the several structural
parameters
should be highly desirable. This statement is particularly true
for the stellar mass of the models. We consider a
set of additional sequences of models within a narrow range of stellar
masses. In the absence of actual self-consistent evolutionary computations
for post-born-again PG 1159 models with different stellar masses, we
elect to create several evolutionary sequences by employing an
artificial procedure starting from our "seed'' model sequence of
0.5895 ![]() (see below). This approach has been adopted
in many pulsation studies aimed at exploring the effects of different
model parameters on the pulsation properties (see, e.g., Kawaler &
Bradley 1994), starting from a post-AGB evolutionary model. At
variance with previous calculations, we derived
additional model sequences with stellar masses in the ranges
0.53-0.58
(see below). This approach has been adopted
in many pulsation studies aimed at exploring the effects of different
model parameters on the pulsation properties (see, e.g., Kawaler &
Bradley 1994), starting from a post-AGB evolutionary model. At
variance with previous calculations, we derived
additional model sequences with stellar masses in the ranges
0.53-0.58 ![]() and
0.60-0.64
and
0.60-0.64 ![]() (with a step of 0.01
(with a step of 0.01 ![]() )
from the post-born-again 0.5895-
)
from the post-born-again 0.5895-![]() sequence previously
described. To this end, we artificially changed the stellar
mass
sequence previously
described. To this end, we artificially changed the stellar
mass![]() to the appropriate values shortly after the end of the
born-again episode. Although this procedure led to a sequence of
unphysical stellar models for which the helium-burning luminosity is
not consistent with the thermo-mechanical structure of the models, we
found that the transitory stage vanishes at high luminosities,
before the star reaches the "knee'' in the
to the appropriate values shortly after the end of the
born-again episode. Although this procedure led to a sequence of
unphysical stellar models for which the helium-burning luminosity is
not consistent with the thermo-mechanical structure of the models, we
found that the transitory stage vanishes at high luminosities,
before the star reaches the "knee'' in the
![]() plane
plane![]() .
This can be understood by examining Fig. 2, which shows
the surface and helium-burning luminosities in terms of the effective
temperature. The upper panel depicts the situation for our consistent
0.5895-
.
This can be understood by examining Fig. 2, which shows
the surface and helium-burning luminosities in terms of the effective
temperature. The upper panel depicts the situation for our consistent
0.5895-![]() sequence. The bottom panel corresponds to the 0.64-
sequence. The bottom panel corresponds to the 0.64-![]() artificially generated sequence. As a result of the change
in the thermal structure of the outer layers induced by the
abrupt change in the stellar mass (at low effective temperatures),
the helium-burning luminosity becomes seriously affected. Note that once
the transitory stage has disappeared, the helium-burning luminosity
follows a similar trend to what is expected from the
full evolutionary computation (upper panel). In the bottom panel,
the unphysical evolutionary stages and the evolutionary stages which
we consider valid for the purposes of this paper are indicated with different line styles. Thus, the tracks depicted in Fig. 1 correspond to
those stages of
the evolutionary sequences for which the unphysical transitory has
long disappeared. We stress that pulsation results presented in
this work have been performed on stellar models belonging to the
evolutionary sequences shown in Fig. 1 (see also
Fig. 3). We warn again that the pulsational
results presented here are based on artificially
constructed stellar models and that full evolutionary models with different stellar masses and complete evolutionary histories are required to put them in a firm context.
artificially generated sequence. As a result of the change
in the thermal structure of the outer layers induced by the
abrupt change in the stellar mass (at low effective temperatures),
the helium-burning luminosity becomes seriously affected. Note that once
the transitory stage has disappeared, the helium-burning luminosity
follows a similar trend to what is expected from the
full evolutionary computation (upper panel). In the bottom panel,
the unphysical evolutionary stages and the evolutionary stages which
we consider valid for the purposes of this paper are indicated with different line styles. Thus, the tracks depicted in Fig. 1 correspond to
those stages of
the evolutionary sequences for which the unphysical transitory has
long disappeared. We stress that pulsation results presented in
this work have been performed on stellar models belonging to the
evolutionary sequences shown in Fig. 1 (see also
Fig. 3). We warn again that the pulsational
results presented here are based on artificially
constructed stellar models and that full evolutionary models with different stellar masses and complete evolutionary histories are required to put them in a firm context.
![\begin{figure}
\par\includegraphics[width=7.4cm,clip]{4199f-02.eps}
\end{figure}](/articles/aa/full/2006/30/aa4199-05/Timg61.gif) |
Figure 2:
The surface (thick line) and helium-burning (thin line)
luminosities (
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[clip,width=8.1cm,clip]{4199f-03.eps}
\end{figure}](/articles/aa/full/2006/30/aa4199-05/Timg63.gif) |
Figure 3:
Evolutionary tracks for sequences with stellar
masses, from right to left, of
|
| Open with DEXTER | |
Since we do not account for the complete evolution of
the progenitor stars (except for the 0.5895-![]() sequence), the
internal composition of the models we use in part of our pulsational
analysis may not be completely realistic, a fact that should be kept
in mind when we analyze, in particular, the dependence of the
asymptotic period spacing and mode trapping properties with the
stellar mass. Also, the shape of the carbon/oxygen
profile - particularly in the core - is quite sensitive to the
adopted reaction rates during the central helium burning phase (see
Kunz et al. 2002; Straniero et al. 2003) and the efficiency of the
convection-induced mixing (overshooting and/or semiconvection; see
Straniero et al. 2003). In particular, we recently found
(Córsico & Althaus 2005) that with a lower rate for the
12C
sequence), the
internal composition of the models we use in part of our pulsational
analysis may not be completely realistic, a fact that should be kept
in mind when we analyze, in particular, the dependence of the
asymptotic period spacing and mode trapping properties with the
stellar mass. Also, the shape of the carbon/oxygen
profile - particularly in the core - is quite sensitive to the
adopted reaction rates during the central helium burning phase (see
Kunz et al. 2002; Straniero et al. 2003) and the efficiency of the
convection-induced mixing (overshooting and/or semiconvection; see
Straniero et al. 2003). In particular, we recently found
(Córsico & Althaus 2005) that with a lower rate for the
12C
![]() O reaction than we adopted here, the
central abundances of oxygen and carbon become quite similar,
partially smoothing the chemical steps in the core. However, as shown
in that paper, the mode trapping structure resulting from the core is
not seriously altered.
O reaction than we adopted here, the
central abundances of oxygen and carbon become quite similar,
partially smoothing the chemical steps in the core. However, as shown
in that paper, the mode trapping structure resulting from the core is
not seriously altered.
In this section we present an extensive adiabatic analysis of our grid of PG 1159 evolutionary models. Since the most detailed and thorough reference in the literature on adiabatic pulsations of PG 1159 stars is the work of Kawaler & Bradley (1994) [hereinafter KB94], we invoke it repeatedly to compare their results with our own findings.
We assessed the pulsation properties of about 3000 stellar models, the stellar mass of which ranges from 0.53 ![]() to 0.64
to 0.64 ![]() ,
embracing the well-established mean mass for WDs.
Figure 3 shows the
evolutionary tracks of our model sequences. All of our PG 1159
sequences are characterized by a helium layer thickness of
0.0088
M* - as predicted by our evolutionary calculations for the
0.5895-
,
embracing the well-established mean mass for WDs.
Figure 3 shows the
evolutionary tracks of our model sequences. All of our PG 1159
sequences are characterized by a helium layer thickness of
0.0088
M* - as predicted by our evolutionary calculations for the
0.5895-![]() models (Althaus et al. 2005). For each analyzed
model we computed g-mode periods in the range 50-2500 s,
although in some cases we have extended the range of periods and also
included p-mode computations. We limited our calculations to the
degrees
models (Althaus et al. 2005). For each analyzed
model we computed g-mode periods in the range 50-2500 s,
although in some cases we have extended the range of periods and also
included p-mode computations. We limited our calculations to the
degrees ![]() because the periods observed in pulsating PG 1159
stars have been positively identified with
because the periods observed in pulsating PG 1159
stars have been positively identified with ![]() (see, e.g.,
Winget et al. 1991; Vauclair et al. 2002). Since one of the purposes
of this work is to get values of adiabatic periods that are
as precise as possible, we employed about
2700-3000 mesh-points
to describe our background stellar models.
(see, e.g.,
Winget et al. 1991; Vauclair et al. 2002). Since one of the purposes
of this work is to get values of adiabatic periods that are
as precise as possible, we employed about
2700-3000 mesh-points
to describe our background stellar models.
We begin this section with a brief description of the pulsation code
employed and the relevant pulsation quantities. For computing
pulsation modes of our PG 1159 models, we use an updated version of the
pulsational code employed in Córsico et al. (2001). Briefly, the
code, which is coupled to the LPCODE evolutionary code, is based on
the general Newton-Raphson technique and solves the full fourth-order
set of equations governing linear, adiabatic, nonradial stellar
pulsations following the dimensionless formulation of Dziembowski
(1971). The pulsation code provides the dimensionless eigenfrequency
![]() - k being the radial order of the mode - and
eigenfunctions
y1,..., y4. From these basic quantities, the
code computes the pulsation periods (
- k being the radial order of the mode - and
eigenfunctions
y1,..., y4. From these basic quantities, the
code computes the pulsation periods (![]() ), the oscillation kinetic
energy (Kk), rotation splitting coefficients (Ck), weight
functions (Wk), and variational periods (
), the oscillation kinetic
energy (Kk), rotation splitting coefficients (Ck), weight
functions (Wk), and variational periods (
![]() )
for each
computed eigenmode. Usually, the relative difference between
)
for each
computed eigenmode. Usually, the relative difference between
![]() and
and ![]() is lower than
is lower than
![]() .
The
pulsation equations, boundary conditions, and relevant adiabatic
quantities are given in Appendix A.
.
The
pulsation equations, boundary conditions, and relevant adiabatic
quantities are given in Appendix A.
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{4199f-04.eps}
\end{figure}](/articles/aa/full/2006/30/aa4199-05/Timg72.gif) |
Figure 4:
The run of the squared Brunt-Väisälä frequency in terms
of the mass coordinate, corresponding to a 0.5895- |
| Open with DEXTER | |
The prescription we follow to assess the run of the
Brunt-Väisälä frequency (N) is the so-called "Ledoux
Modified'' treatment - see Tassoul et al. (1990) - appropriately
generalized to include the effects of having three nuclear species
(oxygen, carbon, and helium) varying in abundance (see KB94). In this
numerical treatment the contribution to N from any change in
composition is almost completely contained in the Ledoux term B
which renders the method particularly useful for inferring the relative
weight that each chemical transition region has on the mode-trapping
properties of the model (see Sect. 3.4). Specifically,
the Brunt-Väisälä frequency is computed as
| |
= | ![$\displaystyle \left[\frac{\partial \ln{p}}
{\partial \ln{T}} \right]_{\rho},~
\chi_{\rm\rho}= \left[\frac{\partial \ln{p}}
{\partial \ln{\rho}} \right]_T,$](/articles/aa/full/2006/30/aa4199-05/img76.gif) |
|
| = | ![$\displaystyle \left[\frac{\partial \ln{p}}
{\partial \ln{X_i}} \right]_{\rho,T,{X_{j \neq i}}}\cdot$](/articles/aa/full/2006/30/aa4199-05/img78.gif) |
(3) |
This section is devoted to exploring the basic
properties of nonradial pulsation modes of our PG 1159 pre-WD
evolutionary models at some length. To this end, we have extended
the scope of our pulsation calculations by including low-order g-modes and also nonradial p-modes in the discussion, although we are aware that
short periods like those associated with such modes have not been ever
detected in variable PG 1159 stars. We have chosen to analyze
the sequence of
![]() -models from the early phases of
evolution at constant luminosity - shortly before the maximum of
effective temperature - until the beginning of the WD cooling track,
when models evolve at a roughly constant radius. We stress that
this is the first time that the adiabatic pulsation properties of
fully evolutionary post born-again PG 1159 models have been assessed, one
exception being the non-adiabatic analysis of Gautschy et al.
(2005). Thus, we believe that it is instructive to look into the
basic features of the full nonradial pulsation spectrum of these
models.
-models from the early phases of
evolution at constant luminosity - shortly before the maximum of
effective temperature - until the beginning of the WD cooling track,
when models evolve at a roughly constant radius. We stress that
this is the first time that the adiabatic pulsation properties of
fully evolutionary post born-again PG 1159 models have been assessed, one
exception being the non-adiabatic analysis of Gautschy et al.
(2005). Thus, we believe that it is instructive to look into the
basic features of the full nonradial pulsation spectrum of these
models.
![\begin{figure}
\par\includegraphics[width=8.1cm,clip]{4199f-05.eps}
\end{figure}](/articles/aa/full/2006/30/aa4199-05/Timg82.gif) |
Figure 5:
The evolution of the |
| Open with DEXTER | |
We begin by describing the evolution of the period spectrum. For the
![]() sequence, we have physically meaningful
stellar models available from stages before the beginning of the WD cooling
track. This allows us to perform an exploratory exercise of the
period spectrum from the moment when the objects still retain the
thermal structure resulting from prior evolution of the progenitor
star. In Fig. 5 we show the
sequence, we have physically meaningful
stellar models available from stages before the beginning of the WD cooling
track. This allows us to perform an exploratory exercise of the
period spectrum from the moment when the objects still retain the
thermal structure resulting from prior evolution of the progenitor
star. In Fig. 5 we show the ![]() pulsation periods
pulsation periods
![]() in terms of the effective temperature before (panel a) and
after (panel b) the model reaches the turning point in the H-R diagram
(see Fig. 3). We find the pulsation periods to decrease in
stages in which the model is still approaching its maximum
effective temperature (
in terms of the effective temperature before (panel a) and
after (panel b) the model reaches the turning point in the H-R diagram
(see Fig. 3). We find the pulsation periods to decrease in
stages in which the model is still approaching its maximum
effective temperature (
![]() K). This is
because the star is undergoing a rapid contraction, in particular in
the outer layers. As is well known, contraction effects lead to a
decrease in the pulsation periods (see Winget et al. 1983). When the
model has already settled into their cooling phase, the periods
increase in response to the decrease in the Brunt-Väisälä
frequency. Thus, the behavior exhibited is typical of WD pulsators,
with increasing periods as the effective temperature decreases. Note
in panel (a) of Fig. 5 that when
K). This is
because the star is undergoing a rapid contraction, in particular in
the outer layers. As is well known, contraction effects lead to a
decrease in the pulsation periods (see Winget et al. 1983). When the
model has already settled into their cooling phase, the periods
increase in response to the decrease in the Brunt-Väisälä
frequency. Thus, the behavior exhibited is typical of WD pulsators,
with increasing periods as the effective temperature decreases. Note
in panel (a) of Fig. 5 that when
![]() K, the low-order periods (
K, the low-order periods (
![]() s) exhibit a behavior
reminiscent of the well-known "avoided crossing''. When a pair of
modes experiences avoided crossing, the modes exchange their intrinsic
properties (see Aizenman et al. 1977). These
are modes with a mixed character, that is, modes that behave as
g-modes in certain zones of the star and as p-modes in other
regions.
s) exhibit a behavior
reminiscent of the well-known "avoided crossing''. When a pair of
modes experiences avoided crossing, the modes exchange their intrinsic
properties (see Aizenman et al. 1977). These
are modes with a mixed character, that is, modes that behave as
g-modes in certain zones of the star and as p-modes in other
regions.
In order to obtain valuable qualitative information on nonradial
pulsations, we apply a local treatment to the pulsation equations (Unno
et al. 1989). Employing the Cowling approximation, in which the
perturbation of the gravitational potential is neglected (![]() ),
and assuming that the coefficients of the pulsation equations are
almost constant - that is, within the limit of high radial order k -
we obtain simple expressions for the eigenfunctions:
),
and assuming that the coefficients of the pulsation equations are
almost constant - that is, within the limit of high radial order k -
we obtain simple expressions for the eigenfunctions:
![]() ,
and a useful dispersion
relation follows:
,
and a useful dispersion
relation follows:
![]() ,
which relates the local radial wave
number kr to the pulsation frequency
,
which relates the local radial wave
number kr to the pulsation frequency ![]() .
Here,
.
Here, ![]() is the
Lamb frequency, defined as
is the
Lamb frequency, defined as
![]() .
If
.
If
![]() or
or
![]() ,
the wave number kr is real, and if
,
the wave number kr is real, and if
![]() or
or
![]() ,
kr is purely imaginary.
,
kr is purely imaginary.
In Fig. 6 we show
![]() and N2 as functions of
and N2 as functions of
![]() .
This type of diagram is called a propagation diagram (see, e.g., Unno et al. 1989; Cox 1980). The
figure corresponds to a PG 1159 model with
.
This type of diagram is called a propagation diagram (see, e.g., Unno et al. 1989; Cox 1980). The
figure corresponds to a PG 1159 model with
![]() ,
,
![]() ,
and
,
and
![]() K. This model
corresponds to a stage at which the star is still approaching its
maximum
K. This model
corresponds to a stage at which the star is still approaching its
maximum
![]() (see the arrow in panel (a) of Fig. 5). Since this model
still retains some similarities to those of the red giants from which
these models are descendants, the Brunt-Väisälä frequency is
characterized by high central values as compared to those
characterizing the outer regions. Pulsation modes should be unable to propagate in the "evanescent'' zones, in which kr is purely imaginary. In contrast, in regions in which kr is real,
modes should be oscillatory in space, and these regions correspond to
"propagation'' zones. Two propagation regions exist, one corresponding to the case
(see the arrow in panel (a) of Fig. 5). Since this model
still retains some similarities to those of the red giants from which
these models are descendants, the Brunt-Väisälä frequency is
characterized by high central values as compared to those
characterizing the outer regions. Pulsation modes should be unable to propagate in the "evanescent'' zones, in which kr is purely imaginary. In contrast, in regions in which kr is real,
modes should be oscillatory in space, and these regions correspond to
"propagation'' zones. Two propagation regions exist, one corresponding to the case
![]() ,
associated with p-modes (P-region), and the other in which
the eigenfrequencies satisfies
,
associated with p-modes (P-region), and the other in which
the eigenfrequencies satisfies
![]() ,
associated with g-modes (G-region). The predictions of this simple
local analysis are nicely confirmed by our full numerical solution.
Indeed, the figure shows the computed eigenfrecuencies of p- and
g-modes and the loci of the nodes of the
radial eigenfunction, y1. No node lies
in the evanescent regions, meaning that the radial eigenfunction is
not oscillatory here. This figure clearly shows that the p-modes
and g-modes are trapped in the P-region and the G-region,
respectively.
,
associated with g-modes (G-region). The predictions of this simple
local analysis are nicely confirmed by our full numerical solution.
Indeed, the figure shows the computed eigenfrecuencies of p- and
g-modes and the loci of the nodes of the
radial eigenfunction, y1. No node lies
in the evanescent regions, meaning that the radial eigenfunction is
not oscillatory here. This figure clearly shows that the p-modes
and g-modes are trapped in the P-region and the G-region,
respectively.
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{4199f-06.eps}
\end{figure}](/articles/aa/full/2006/30/aa4199-05/Timg101.gif) |
Figure 6:
Propagation diagram corresponding to a PG 1159 evolutionary
model characterized by
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{4199f-07.eps}
\end{figure}](/articles/aa/full/2006/30/aa4199-05/Timg103.gif) |
Figure 7:
Same of Fig. 6, but for a PG 1159 model
characterized by
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{4199f-08.eps}
\end{figure}](/articles/aa/full/2006/30/aa4199-05/Timg104.gif) |
Figure 8:
The normalized weight function of the mode g40
vs. the stellar radius corresponding to
|
| Open with DEXTER | |
Because the very peculiar shape of the Brunt-Väisälä
frequency in the inner regions of the star, there is a considerable
range of intermediate frequencies in which the inner parts of the star
lie predominantly in the G-region, and the outer parts lie in the
P-region. Thus, these intermediate-frequency modes possess a mixed
character: they behave like g-modes in the inner parts of the star
and like p-modes in the outer parts. Nodes in y1 for
such modes may occur in both the P- and G-regions. In order to get the
radial order of these modes we employ the scheme of Scuflaire
(1974)![]() . In the figure, modes with mixed
character and some low-order "pure'' p- and g-modes are
appropriately labeled.
. In the figure, modes with mixed
character and some low-order "pure'' p- and g-modes are
appropriately labeled.
Figure 7 shows a propagation diagram corresponding to a model
characterized by
![]() ,
,
![]() and
and
![]() K. Unlike the model described in
Fig. 6, this PG 1159 model is already located at the early
WD cooling track - its effective temperature is marked with an arrow
in panel (b) of Fig. 5. The fundamental
properties of its pulsational spectrum should be reminiscent
of the pulsating WD stars. In fact, the Brunt-Väisälä frequency
shows higher values in the outer regions than in the core, such
that the propagation regions P and G are markedly separated. As a
result, modes with mixed character no longer exist, and the families
of g- and p-modes are clearly differentiated. The
radial order of the modes is simply the number of the nodes of the
radial eigenfunction. For this model, the g-modes are free
to propagate throughout the star, at variance with the situation of
the model described in Fig. 6, where g-modes are
strongly confined to the core region.
K. Unlike the model described in
Fig. 6, this PG 1159 model is already located at the early
WD cooling track - its effective temperature is marked with an arrow
in panel (b) of Fig. 5. The fundamental
properties of its pulsational spectrum should be reminiscent
of the pulsating WD stars. In fact, the Brunt-Väisälä frequency
shows higher values in the outer regions than in the core, such
that the propagation regions P and G are markedly separated. As a
result, modes with mixed character no longer exist, and the families
of g- and p-modes are clearly differentiated. The
radial order of the modes is simply the number of the nodes of the
radial eigenfunction. For this model, the g-modes are free
to propagate throughout the star, at variance with the situation of
the model described in Fig. 6, where g-modes are
strongly confined to the core region.
The regions of the star that most contribute to the period formation
are inferred from Fig. 8, which shows the normalized weight
function (Eq. (A.14) of the Appendix) of a g-mode with
![]() in terms of the stellar radius
corresponding to
in terms of the stellar radius
corresponding to
![]() -models at different effective
temperatures. The location of these models in the H-R diagram is
depicted as black dots in Fig. 3. For the model
at
-models at different effective
temperatures. The location of these models in the H-R diagram is
depicted as black dots in Fig. 3. For the model
at
![]() K (panel a), Wk adopts
appreciable amplitudes only in central regions. Since the behavior of
the weight function for this mode is representative of all g-modes
with intermediate and high radial order k, we conclude that the
g-mode pulsation periods for PG 1159 models that have not
reached still the maximum in
K (panel a), Wk adopts
appreciable amplitudes only in central regions. Since the behavior of
the weight function for this mode is representative of all g-modes
with intermediate and high radial order k, we conclude that the
g-mode pulsation periods for PG 1159 models that have not
reached still the maximum in
![]() are mostly determined by the core
regions of the star, irrespective of the structure of the outer
layers. Thus, for models in high-luminosity phases, the adiabatic
pulsations properties reflect the conditions in the degenerate core.
The situation for a model placed exactly at the turning point in
are mostly determined by the core
regions of the star, irrespective of the structure of the outer
layers. Thus, for models in high-luminosity phases, the adiabatic
pulsations properties reflect the conditions in the degenerate core.
The situation for a model placed exactly at the turning point in
![]() is depicted in panel (b) of Fig. 5,
corresponding to
is depicted in panel (b) of Fig. 5,
corresponding to
![]() K and
K and
![]() .
At this stage, the regions of period formation have
extended towards more external zones. By the time the model has
settled into its WD cooling track, the weight function exhibits
appreciable values throughout the star, having some amplitude also in
the outer regions, as displayed in panel (c). Below
.
At this stage, the regions of period formation have
extended towards more external zones. By the time the model has
settled into its WD cooling track, the weight function exhibits
appreciable values throughout the star, having some amplitude also in
the outer regions, as displayed in panel (c). Below
![]() K, the weight function adopts its maximum value in the outer layers,
as can be seen in panels (d) and (e). At these stages, the adiabatic
periods are mainly determined by the outer envelope, although the
inner regions of the star also contribute to establishing the period
of oscillation. Our findings fully agree with the results of
the early computations of Kawaler et al. (1985) - for instance,
compare our Fig. 8 with their Fig. 5.
K, the weight function adopts its maximum value in the outer layers,
as can be seen in panels (d) and (e). At these stages, the adiabatic
periods are mainly determined by the outer envelope, although the
inner regions of the star also contribute to establishing the period
of oscillation. Our findings fully agree with the results of
the early computations of Kawaler et al. (1985) - for instance,
compare our Fig. 8 with their Fig. 5.
In the asymptotic limit of very high radial order k (long periods),
the periods of g-modes of a chemically homogeneous stellar model for
a given degree ![]() and consecutive k are separated by a constant
period spacing
and consecutive k are separated by a constant
period spacing
![]() ,
given by (Tassoul
et al. 1990):
,
given by (Tassoul
et al. 1990):
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{4199f-09.eps}
\end{figure}](/articles/aa/full/2006/30/aa4199-05/Timg118.gif) |
Figure 9:
The evolution of |
| Open with DEXTER | |
The evolution of ![]() vs. the stellar luminosity for models with
different stellar masses is displayed in Fig. 9. In line
with previous works (see, e.g., KB94), our results indicate that
vs. the stellar luminosity for models with
different stellar masses is displayed in Fig. 9. In line
with previous works (see, e.g., KB94), our results indicate that
![]() increases with decreasing stellar mass. In particular, the
value of
increases with decreasing stellar mass. In particular, the
value of ![]() exhibits an increment of about 6-8 s when the
stellar mass decreases about
exhibits an increment of about 6-8 s when the
stellar mass decreases about
![]() .
This is due to the fact
that the asymptotic period spacing is inversely proportional to the
integral of N (Eq. (4)). As we go to lower stellar
masses, the Brunt-Väisälä frequency decreases; consequently
.
This is due to the fact
that the asymptotic period spacing is inversely proportional to the
integral of N (Eq. (4)). As we go to lower stellar
masses, the Brunt-Väisälä frequency decreases; consequently
![]() goes up.
goes up.
Figure 9 shows that ![]() is also a function of the stellar
luminosity, although the dependence is much weaker than the dependence
on the stellar mass. As documented by the figure, for
is also a function of the stellar
luminosity, although the dependence is much weaker than the dependence
on the stellar mass. As documented by the figure, for
![]() - depending on the stellar
mass - the period spacing increases with decreasing
luminosity. This can be explained on the basis that, due to the
increasing degeneracy in the core as the star cools, the
Brunt-Väisälä frequency gradually decreases, causing a slow
increment in the magnitude of
- depending on the stellar
mass - the period spacing increases with decreasing
luminosity. This can be explained on the basis that, due to the
increasing degeneracy in the core as the star cools, the
Brunt-Väisälä frequency gradually decreases, causing a slow
increment in the magnitude of ![]() .
Finally, since we
do not consider different helium layer mass values in this work,
we have not been able to assess the possible dependence of the asymptotic period spacing on
.
Finally, since we
do not consider different helium layer mass values in this work,
we have not been able to assess the possible dependence of the asymptotic period spacing on
![]() .
However, this dependence is expected to be
very weak (see KB94).
.
However, this dependence is expected to be
very weak (see KB94).
As we mentioned, the period spectrum of chemically homogeneous stellar models is characterized by a constant period separation, given very accurately by Eq. (4). However, current evolutionary calculations predicts that PG 1159 stars - as well as (hydrogen-rich) DA and (helium-rich) DB WD stars - must have composition gradients in their interiors, something that the observation also indicates. The presence of one or more narrow regions in which the abundances of nuclear species are rapidly varying strongly modifies the character of the resonant cavity in which modes should propagate as standing waves - the propagation region. Specifically, chemical interfaces act like reflecting boundaries that partially trap certain modes, forcing them to oscillate with larger amplitudes in specific regions - bounded either by two interfaces or by one interface and the stellar center or surface - and with smaller amplitudes outside of those regions.
The requirement for a mode to be trapped is that the wavelength of its radial eigenfunction matches the spatial separation between two interfaces or between one interface and the stellar center or surface. This mechanical resonance, known as mode trapping, has been the subject of intense study in the context of stratified DA and DB WD pulsations: see, e.g., Brassard et al. (1992), Bradley et al. (1993), Córsico et al. (2002). In the field of PG 1159 stars, mode trapping has been extensively explored by KB94; we refer the reader to that work for details.
There are (at least) two ways to identify trapped modes in a given stellar model. First, we can consider the oscillation kinetic energy, Kk. Because the amplitude of eigenfunctions is arbitrarily normalized at the model surface in our calculations (see the Appendix), the values of the kinetic energy are useful only in a relative sense. Here, Kk is proportional to the integral of the squared amplitude of eigenfunctions, weighted by the density (see Eq. (A.13) in the Appendix). Thus, modes propagating in the deep interior of the star, where densities are very high, will exhibit higher values than modes that are oscillating in the low-density, external regions. When only a single chemical interface is present, modes can be classified as modes trapped in the outer layers, as modes confined in the core regions, or simply as "normal modes'' - which oscillate everywhere in the star - characterized by low, high, and intermediate Kk values, respectively (see Brassard et al. 1992). This rather simple picture becomes markedly complex when the stellar model is characterized by several chemical composition gradients - see Córsico et al. (2002) for the case of ZZ Ceti models.
![\begin{figure}
\par\includegraphics[width=8.3cm,clip]{4199f-10.eps}
\end{figure}](/articles/aa/full/2006/30/aa4199-05/Timg122.gif) |
Figure 10:
The forward period spacing
|
| Open with DEXTER | |
A second and, more important from an observational point of view,
consequence of mode trapping is that the period spacing
![]() ,
when plotted in terms of the pulsation period
,
when plotted in terms of the pulsation period
![]() ,
exhibits strong departures from uniformity. It is the
period difference between an observed mode and adjacent modes (
,
exhibits strong departures from uniformity. It is the
period difference between an observed mode and adjacent modes (
![]() )
that is the observational diagnostic of mode trapping -
at variance with Kk, whose value is very difficult to estimate
only from observation. For stellar models characterized by a single
chemical interface, local minima in
)
that is the observational diagnostic of mode trapping -
at variance with Kk, whose value is very difficult to estimate
only from observation. For stellar models characterized by a single
chemical interface, local minima in
![]() usually
correspond directly to modes trapped in the outer layers, whereas
local maxima in
usually
correspond directly to modes trapped in the outer layers, whereas
local maxima in
![]() are associated to modes trapped in
the core region.
are associated to modes trapped in
the core region.
We now turn to the specific case of our PG 1159 pre-WD models. As Fig. 4 shows, they exhibit several chemical interfaces, some associated with the various steps in the 16O and 12C profile at the core region, and a single, more external transition region in which oxygen, carbon, and helium are continuously varying (see Fig. 4). As stated in Sect. 3.1, these composition gradients produce pronounced peaks in the Brunt-Väisälä frequency - through the Ledoux term - that strongly disturb the structure of the period spectrum.
The influence of the chemical composition gradients inside our
PG 1159 models on their period spectra is clearly shown in panel (a) of Fig. 10, in which the ![]() period
spacing is plotted in terms of the periods for a reference model
characterized by a stellar mass of
period
spacing is plotted in terms of the periods for a reference model
characterized by a stellar mass of
![]() ,
an effective
temperature of 139 000 K, and a luminosity of
,
an effective
temperature of 139 000 K, and a luminosity of
![]() .
The
plot shows very rapid variations in
.
The
plot shows very rapid variations in
![]() everywhere in the
period spectrum, with "trapping amplitudes'' up to about 6 s and an
asymptotic period spacing of
everywhere in the
period spectrum, with "trapping amplitudes'' up to about 6 s and an
asymptotic period spacing of ![]() 20.94 s. The rather complex
period-spacing diagram shown by Fig. 10 is typical of
models characterized by several chemical interfaces. In order to
isolate the effect of each chemical composition gradient on mode
trapping, we follow the procedure of Charpinet et al. (2000) for
models of sdB stars - see also Brassard et al. (1992) for the case
of ZZ Ceti stars. Specifically, we minimize, but do no
completely eliminate, the effects of a given chemical interface
simply by forcing the Ledoux term B to be zero in the specific
region of the star in which such an interface is located. In this way,
the resulting mode trapping will only be due to the remaining chemical
interfaces. In the interest of clarity, we label the contribution to B due to the O/C/He chemical interface at
20.94 s. The rather complex
period-spacing diagram shown by Fig. 10 is typical of
models characterized by several chemical interfaces. In order to
isolate the effect of each chemical composition gradient on mode
trapping, we follow the procedure of Charpinet et al. (2000) for
models of sdB stars - see also Brassard et al. (1992) for the case
of ZZ Ceti stars. Specifically, we minimize, but do no
completely eliminate, the effects of a given chemical interface
simply by forcing the Ledoux term B to be zero in the specific
region of the star in which such an interface is located. In this way,
the resulting mode trapping will only be due to the remaining chemical
interfaces. In the interest of clarity, we label the contribution to B due to the O/C/He chemical interface at
![]() as "
as "
![]() '', and "
'', and "
![]() '' the contribution to B associated
with the O/C chemical interface at
'' the contribution to B associated
with the O/C chemical interface at
![]() - see inset of Fig. 4. Specifically, we
have recomputed the entire g-mode period spectrum under the
following assumptions: (1)
- see inset of Fig. 4. Specifically, we
have recomputed the entire g-mode period spectrum under the
following assumptions: (1)
![]() and
and
![]() ,
(2)
,
(2)
![]() and
and
![]() ,
and (3)
,
and (3)
![]() and
and
![]() (B=0 in all regions). The results are shown
in panels (b), (c) and (d) of Fig. 10, respectively. By
comparing the different cases illustrated, an important conclusion
emerges from this figure: the chemical transition region at
(B=0 in all regions). The results are shown
in panels (b), (c) and (d) of Fig. 10, respectively. By
comparing the different cases illustrated, an important conclusion
emerges from this figure: the chemical transition region at
![]() is responsible for the non-uniformities in
is responsible for the non-uniformities in
![]() only for
only for
![]() s (panel c), whereas the chemical composition gradients
in the core region (
s (panel c), whereas the chemical composition gradients
in the core region (
![]() )
cause the mode-trapping
structure in the rest of the period spectrum (panel b). When B= 0everywhere inside the model (panel d), the period-spacing diagram is
characterized by the absence of strong features of mode trapping,
although some structure remains, in particular for low-order
modes. Note the nice agreement between the numerical computations of
)
cause the mode-trapping
structure in the rest of the period spectrum (panel b). When B= 0everywhere inside the model (panel d), the period-spacing diagram is
characterized by the absence of strong features of mode trapping,
although some structure remains, in particular for low-order
modes. Note the nice agreement between the numerical computations of
![]() and the predictions of the asymptotic theory given by
Eq. (4) for the limit
and the predictions of the asymptotic theory given by
Eq. (4) for the limit ![]() .
.
From the above discussion, it is clear that the mode-trapping features characterizing our PG 1159 models are inflicted by the stepped shape of the carbon/oxygen chemical profile at the core - left by prior convective overshooting - at least for the range of periods observed in GW Vir stars. The more external chemical transition has a minor influence, except for the regime of short periods. This situation is more evident for the more massive PG 1159 models than for the less massive ones.
The findings outlined above are clearly at odds with previous results
reported by KB94. Indeed, these authors have found that the
mode-trapping properties of their PG 1159 models are fixed mainly by
the outer O/C/He transition region, to such a degree that they
are able to employ mode-trapping signatures as a sensitive locator of
this transition region. The origin of this discrepancy can be found
in the details of the input physics employed in building up the
background stellar models. Of particular interest here is the presence
of a much less pronounced chemical transition in the outer parts of
the C/O core of the KB94 models, as compared with the rather abrupt
chemical gradients at
![]() characterizing our PG 1159 models. If we artificially minimize the effect of this
transition region - by setting
characterizing our PG 1159 models. If we artificially minimize the effect of this
transition region - by setting
![]() - we immediately
recover the results of KB94. Indeed, the period-spacing diagram of
panel (c) in our Fig. 10 looks very similar the one shown
in Fig. 3 of KB94, corresponding to
- we immediately
recover the results of KB94. Indeed, the period-spacing diagram of
panel (c) in our Fig. 10 looks very similar the one shown
in Fig. 3 of KB94, corresponding to
![]() .
We
note, however, that the "trapping cycle'' - the period interval
between two period-spacing minima - of our modified model (c) is
.
We
note, however, that the "trapping cycle'' - the period interval
between two period-spacing minima - of our modified model (c) is
![]() 70 s, whereas the value of the KB94 model is
70 s, whereas the value of the KB94 model is ![]() 95 s. This difference is due mainly to our model having a more
massive helium envelope (
95 s. This difference is due mainly to our model having a more
massive helium envelope (
![]() )
than in of KB94.
)
than in of KB94.
By means of a simple numerical experiment we have identified the main
source of mode trapping as due to the step-like chemical transition
region located at the core. We now return to panel (a) of
Fig. 10, and note that there is a kind of "beating''
modulating the trapping amplitude. We also note that this striking
feature (seen in all of our models) persists even in the case in which
the effect of the O/C/He transition is artificially minimized, as
illustrated in panel (b). We find that the beating exhibited
by the period-spacing distribution is due to the combined
mode-trapping effects caused by the various steps in the O/C chemical
profile in the core. In fact, by performing period computations in
which only the highest peak of the Ledoux term at
![]() (see inset of Fig. 4) is considered, the beating
effect virtually vanishes, and the trapping amplitude becomes nearly
constant.
(see inset of Fig. 4) is considered, the beating
effect virtually vanishes, and the trapping amplitude becomes nearly
constant.
Finally, to better understand the details of the mode-trapping properties of
our models, we resort to the kinetic energy of modes. In
Fig. 11 we plot the period spacing and the kinetic energy
distribution (upper and lower panels, respectively) for the same PG
1159 model considered in panel (a) of Fig. 10. We connect
each minimum in
![]() with their
corresponding value of Kk. In spite of the strong
non-uniformities exhibited by
with their
corresponding value of Kk. In spite of the strong
non-uniformities exhibited by
![]() ,
the Kk values of
adjacent modes do not seem to be very different. However, a
closer inspection of the figure reveals that in most cases a
minimum in
,
the Kk values of
adjacent modes do not seem to be very different. However, a
closer inspection of the figure reveals that in most cases a
minimum in
![]() corresponds to a local maximum in Kk.
Our results strongly suggest that modes associated with minima in
the period-spacing diagram usually correspond to maxima in the kinetic
energy distribution. They should be modes characterized by relatively
large amplitude of their eigenfunctions and weight functions in the
high-density environment characterizing the stellar core.
corresponds to a local maximum in Kk.
Our results strongly suggest that modes associated with minima in
the period-spacing diagram usually correspond to maxima in the kinetic
energy distribution. They should be modes characterized by relatively
large amplitude of their eigenfunctions and weight functions in the
high-density environment characterizing the stellar core.
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{4199f-11.eps}
\end{figure}](/articles/aa/full/2006/30/aa4199-05/Timg137.gif) |
Figure 11:
Period-spacing diagram and kinetic energy
distribution ( upper and lower panels, respectively) for the same PG
1159 model considered in panel (a) of Fig. 10. Vertical
dotted lines link local minima in
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{4199f-12.eps}
\end{figure}](/articles/aa/full/2006/30/aa4199-05/Timg138.gif) |
Figure 12: The spatial run of the modulus of the eigenfunctions y1 and y2, shown in panels b) and c), respectively, and the weight function Wk depicted in panels d) and e), for dipole pulsation modes with k= 56 (thick line) and k= 58 (thin line) corresponding to the same PG 1159 model analyzed in Fig. 11. We also include the Ledoux term B and the abundance (by mass) of 16O, 12C, and 4He in panel a). |
| Open with DEXTER | |
This is precisely what we found after carefully examining the
eigenfunctions at the deepest regions of the core. In panels (b) and (c) of Fig. 12, we show the logarithm of the absolute
value of the eigenfunctions y1 and y2 (see Eq. (A.8) of the
Appendix for their definition), respectively, in terms of the
dimensionless radius x=r/R, for a mode having a local maxima in
kinetic energy (k= 58) and for a mode having a local
minima in Kk (k= 56). Below
![]() ,
the eigenfunctions of the k= 58 mode have larger amplitudes
than that of the k= 56 mode, explaining why the k= 58 mode has a
relatively large oscillation kinetic energy. Modes like the k= 58one are partially trapped in the core region, below the O/C chemical
interface (see panel a). These modes generally correspond
to minima in the period-spacing diagram. In panels (d) and (e) of Fig. 12 the normalized weight function (Wk)
is displayed for the k= 56 and k= 58 modes, respectively.
The relative values of Wk for a given
pulsation mode provide information about the specific regions inside
the star that most contribute to the period formation. From
Fig. 12 for the k= 58 mode the maximum of
Wk is identified with the O/C chemical interface at
,
the eigenfunctions of the k= 58 mode have larger amplitudes
than that of the k= 56 mode, explaining why the k= 58 mode has a
relatively large oscillation kinetic energy. Modes like the k= 58one are partially trapped in the core region, below the O/C chemical
interface (see panel a). These modes generally correspond
to minima in the period-spacing diagram. In panels (d) and (e) of Fig. 12 the normalized weight function (Wk)
is displayed for the k= 56 and k= 58 modes, respectively.
The relative values of Wk for a given
pulsation mode provide information about the specific regions inside
the star that most contribute to the period formation. From
Fig. 12 for the k= 58 mode the maximum of
Wk is identified with the O/C chemical interface at
![]() ,
and the largest amplitude portion of the weight function is
located in the deepest regions of the core (
,
and the largest amplitude portion of the weight function is
located in the deepest regions of the core (
![]() ). For
values of r/R slightly higher than 0.3, the weight function
abruptly diminishes and then reaches a secondary maximum in the region
in which 12C becomes more abundant than 16O. Above this
region Wk exhibits another secondary maximum at the O/C/He transition
zone (
). For
values of r/R slightly higher than 0.3, the weight function
abruptly diminishes and then reaches a secondary maximum in the region
in which 12C becomes more abundant than 16O. Above this
region Wk exhibits another secondary maximum at the O/C/He transition
zone (
![]() ), and above this the weight function
adopts somewhat lower values (
), and above this the weight function
adopts somewhat lower values (
![]() ). Thus, the shape of
the weight function for the k= 58 mode strongly suggests that the
deepest regions of the core have the greater impact on the period
formation of this mode. This conclusion, not surprisingly,
completely agrees with the relatively high value of the oscillation kinetic energy. The
situation is markedly different for the case of the k= 56 mode, as
clearly demonstrated by panel (d) of the figure. For this mode,
most regions of the star contribute appreciably to the formation of
its period. In particular, the most important contributions occur in
regions located at
). Thus, the shape of
the weight function for the k= 58 mode strongly suggests that the
deepest regions of the core have the greater impact on the period
formation of this mode. This conclusion, not surprisingly,
completely agrees with the relatively high value of the oscillation kinetic energy. The
situation is markedly different for the case of the k= 56 mode, as
clearly demonstrated by panel (d) of the figure. For this mode,
most regions of the star contribute appreciably to the formation of
its period. In particular, the most important contributions occur in
regions located at
![]() .
.
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{4199f-13.eps}
\end{figure}](/articles/aa/full/2006/30/aa4199-05/Timg146.gif) |
Figure 13:
The period-spacing distributions for
PG 1159 models with stellar masses, from bottom to top:
|
| Open with DEXTER | |
After having identified the physical
origins and nature of mode trapping in our PG 1159 models, we now
explore the effect of changing the stellar mass M* on the
period-spacing diagrams and mode trapping. We employed model sequences with stellar masses in the ranges
0.53-0.58 ![]() and
0.60-0.64
and
0.60-0.64 ![]() with a step of 0.01
with a step of 0.01 ![]() ,
in addition to the 0.5895-
,
in addition to the 0.5895-![]() sequence previously
described. Those sequences were obtained from the
0.5895-
sequence previously
described. Those sequences were obtained from the
0.5895-![]() sequence by artificially changing the stellar mass
according to the procedure outlined in Sect. 2. Thus,
the results derived in this section could change if the complete
evolution of progenitor stars with different stellar masses were
accounted for. From the asymptotic theory outlined in Sect. 3.3, we know that
sequence by artificially changing the stellar mass
according to the procedure outlined in Sect. 2. Thus,
the results derived in this section could change if the complete
evolution of progenitor stars with different stellar masses were
accounted for. From the asymptotic theory outlined in Sect. 3.3, we know that
![]() decreases when
the stellar mass increases, as is evident from Fig. 9. The asymptotic period spacing is
very close to the average of the computed period spacings
decreases when
the stellar mass increases, as is evident from Fig. 9. The asymptotic period spacing is
very close to the average of the computed period spacings
![]() .
As a result, the average of the computed
period spacing must also decrease as the stellar mass increases.
.
As a result, the average of the computed
period spacing must also decrease as the stellar mass increases.
![]() decreases from 23.19 s to 18.69s when we increase the stellar mass from
decreases from 23.19 s to 18.69s when we increase the stellar mass from
![]() to
to
![]() for a fixed
for a fixed
![]() K.
K.
We also expect variations in the amplitude and cycle of trapping when
we consider changes in the stellar mass. Figure 13
depicts period-spacing diagrams for PG 1159 models with values of M*covering the complete set of stellar masses considered in this work,
for a fixed effective temperature of
![]() K.
The trapping amplitude decreases when the stellar mass
increases. In fact, the maximum of the trapping amplitude is about
10 s for
K.
The trapping amplitude decreases when the stellar mass
increases. In fact, the maximum of the trapping amplitude is about
10 s for
![]() ,
whereas it assumes a value of
,
whereas it assumes a value of ![]() 5 s, at most, for
5 s, at most, for
![]() .
This is a direct consequence of an
increased electron degeneracy in the core of our more massive models,
which in turn produces a weakening in the efficiency of mode
trapping. Another striking feature observed in Fig. 13 is
the decrease in the period of the trapping cycle and the shift of
mode-trapping features to lower periods as we go to higher values of the
stellar mass. Specifically, the portions of the period-spacing diagram
centered at
.
This is a direct consequence of an
increased electron degeneracy in the core of our more massive models,
which in turn produces a weakening in the efficiency of mode
trapping. Another striking feature observed in Fig. 13 is
the decrease in the period of the trapping cycle and the shift of
mode-trapping features to lower periods as we go to higher values of the
stellar mass. Specifically, the portions of the period-spacing diagram
centered at
![]() ,
and
,
and
![]() s for the model with
s for the model with
![]() ,
move to
regions centered at
,
move to
regions centered at
![]() ,
and
,
and
![]() s, respectively, for the model with
s, respectively, for the model with
![]() .
This effect can be understood on the basis that,
while the O/C chemical structure remains at the same Mr/M* value
inside the model when we consider higher stellar masses, its location
in terms of the radial coordinate (r) shifts away from the stellar
center, from
.
This effect can be understood on the basis that,
while the O/C chemical structure remains at the same Mr/M* value
inside the model when we consider higher stellar masses, its location
in terms of the radial coordinate (r) shifts away from the stellar
center, from
![]() for
for
![]() to
to
![]() for
for
![]() .
A similar effect has been
found by Córsico et al. (2005) in the context of crystallizing ZZ Ceti models by considering a fixed value of M* but with the inner
turning point of the g-mode eigenfunctions - the crystallization
front - moving outwards.
.
A similar effect has been
found by Córsico et al. (2005) in the context of crystallizing ZZ Ceti models by considering a fixed value of M* but with the inner
turning point of the g-mode eigenfunctions - the crystallization
front - moving outwards.
In closing this section, we explore the evolution of the
mode-trapping properties as our PG 1159 evolve to cooler temperatures.
As mentioned earlier, the asymptotic period spacing
![]() and the average of the computed period spacings
and the average of the computed period spacings
![]() increase when the stellar luminosity
decreases (see Fig. 9). When the star evolves along the WD
cooling track, a decreasing effective temperature is usually
associated to a decreasing stellar luminosity. As a result, we also
expect that
increase when the stellar luminosity
decreases (see Fig. 9). When the star evolves along the WD
cooling track, a decreasing effective temperature is usually
associated to a decreasing stellar luminosity. As a result, we also
expect that
![]() and
and
![]() increase as cooling proceeds. This trend is confirmed by
our pulsation computations. In fact,
increase as cooling proceeds. This trend is confirmed by
our pulsation computations. In fact,
![]() increases from 20.22 s to
increases from 20.22 s to
![]() s when the effective
temperature decreases from 170 000 K to 70 000 K in a model
with
s when the effective
temperature decreases from 170 000 K to 70 000 K in a model
with
![]() .
The explanation of this effect is
straightforward. As the star cools, its core becomes more degenerate
and the Brunt-Väisälä frequency decreases because
.
The explanation of this effect is
straightforward. As the star cools, its core becomes more degenerate
and the Brunt-Väisälä frequency decreases because
![]() goes down (see Eq. (1)). As a result, the pulsation
periods become longer and the period spacing and the average of
the period spacing must increase.
goes down (see Eq. (1)). As a result, the pulsation
periods become longer and the period spacing and the average of
the period spacing must increase.
To see the effect of changes in the effective temperature
on the trapping cycle and amplitude and to have a global picture of what
happens when the effective temperature changes, we depict
the evolution of the period spacing for
0.5895-![]() models (Fig. 14), shown at different effective temperatures (indicated to the right of the plot) starting from a stage where
the model is still approaching its maximum
models (Fig. 14), shown at different effective temperatures (indicated to the right of the plot) starting from a stage where
the model is still approaching its maximum
![]() (lowest
curve) up to a phase where the object is already on the WD cooling track (upper curve). Note that the scale to the left of the plot
makes sense only for the lowest curve; the remaining curves are shifted
upward for clarity. The figure emphasizes the noticeable
changes that the period-spacing structure undergoes as the effective
temperature varies. Note that there are two clearly different
trends. At stages where the effective temperature increases (before
the star reaches its hot turning point at
(lowest
curve) up to a phase where the object is already on the WD cooling track (upper curve). Note that the scale to the left of the plot
makes sense only for the lowest curve; the remaining curves are shifted
upward for clarity. The figure emphasizes the noticeable
changes that the period-spacing structure undergoes as the effective
temperature varies. Note that there are two clearly different
trends. At stages where the effective temperature increases (before
the star reaches its hot turning point at
![]() K), the mode-trapping features move slowly toward short
periods. This is due to the fact that pulsation periods decrease in
response to the overall warming of the star and that the outer layers
contract. When the star has already passed through its hottest phase,
the opposite behavior is exhibited by the mode-trapping features.
Indeed, maxima and minima values of the period-spacing distributions
move to higher periods when the effective temperature diminishes, in
particular, below
K), the mode-trapping features move slowly toward short
periods. This is due to the fact that pulsation periods decrease in
response to the overall warming of the star and that the outer layers
contract. When the star has already passed through its hottest phase,
the opposite behavior is exhibited by the mode-trapping features.
Indeed, maxima and minima values of the period-spacing distributions
move to higher periods when the effective temperature diminishes, in
particular, below
![]() K. Finally,
the trapping amplitude increases when the effective temperature
decreases.
K. Finally,
the trapping amplitude increases when the effective temperature
decreases.
![\begin{figure}
\par\includegraphics[clip,width=8.4cm,clip]{4199f-14.eps}
\end{figure}](/articles/aa/full/2006/30/aa4199-05/Timg161.gif) |
Figure 14:
Period-spacing distributions for
0.5895- |
| Open with DEXTER | |
To infer the main structural
parameters (that is, M* and
![]() )
of several GW Vir stars,
we employ the results of our extensive period computations
described in previous sections. Because we have not been able to compute realistic PG 1159 models with stellar
masses other than
)
of several GW Vir stars,
we employ the results of our extensive period computations
described in previous sections. Because we have not been able to compute realistic PG 1159 models with stellar
masses other than
![]() in the low-gravity phases (before
the star reaches the "knee'' at the highest value of
in the low-gravity phases (before
the star reaches the "knee'' at the highest value of
![]() ;
see Fig. 1), we have limited ourselves to only
making seismic inferences for the high-gravity members of the GW Vir class, that
is, the naked - stars without surrounding nebulae - variables PG 1159-035, PG 2131+066,
PG 1707+427, and PG 0122+200.
;
see Fig. 1), we have limited ourselves to only
making seismic inferences for the high-gravity members of the GW Vir class, that
is, the naked - stars without surrounding nebulae - variables PG 1159-035, PG 2131+066,
PG 1707+427, and PG 0122+200.
Because changes in the thickness of the surface helium-rich layer and in the surface composition affect the trapping cycle and amplitude (see KB94),
it is possible to fine tune the trapping cycle and the trapping amplitude to match the period spectrum of a given star by adopting these quantities as free adjustable parameters. In spite of this, we prefer to keep the thickness of the helium layer and the surface composition fixed by adopting the values
predicted by our evolutionary computations for these parameters. All of these naked GW Vir stars exhibit very similar surface
abundances
![]() .
Our PG 1159 models are
characterized by surface abundances of (0.000, 0.306, 0.376, 0.228),
so they are very appropriate for our purposes. Before going on to
seismic applications of our bank of periods, we summarize the basic
properties of the cited GW Vir stars below.
.
Our PG 1159 models are
characterized by surface abundances of (0.000, 0.306, 0.376, 0.228),
so they are very appropriate for our purposes. Before going on to
seismic applications of our bank of periods, we summarize the basic
properties of the cited GW Vir stars below.
The four naked GW Vir stars have higher gravity (
![]() )
than the PNNVs and are thought to be slightly more evolved. From
a pulsation point of view, the only difference between both types of
variable stars is that PNNV stars usually pulsate with longer
periods (about
1000 - 3000 s) than the naked
GW Vir which pulsate with periods below 1000 s. Specifically,
there is a well-defined correlation between the luminosity of the star
and the periods exhibited: the more luminous the star, the longer
the pulsation periods.
)
than the PNNVs and are thought to be slightly more evolved. From
a pulsation point of view, the only difference between both types of
variable stars is that PNNV stars usually pulsate with longer
periods (about
1000 - 3000 s) than the naked
GW Vir which pulsate with periods below 1000 s. Specifically,
there is a well-defined correlation between the luminosity of the star
and the periods exhibited: the more luminous the star, the longer
the pulsation periods.
- PG 1159-035: the prototype of the PG 1159
spectral class and also the prototype of the GW Vir pulsators. After
the discovery of its variability by McGraw et al. (1979), PG 1159-035
became the target of an intense observational scrutiny. The most
fruitful analysis of its light curve was carried out by Winget et al.
(1991) employing the high-quality data from the Whole Earth Telescope
(WET; Nather et al. 1990). This analysis showed that PG 1159-035
pulsate in more than 100 independent modes with periods between 300 and 800 s. By using 20 unambiguously identified
![]() periods between 430 and 817 s, KB94 determined a mass for PG 1159-035
of
periods between 430 and 817 s, KB94 determined a mass for PG 1159-035
of
![]() ,
an effective temperature of
,
an effective temperature of
![]() K, and a surface gravity of
K, and a surface gravity of
![]() .
In addition, a
stellar luminosity of
.
In addition, a
stellar luminosity of
![]() and a distance of 440 pc from
the Earth were inferred. On the other hand, spectroscopic analysis by
Dreizler & Heber (1998) yield
and a distance of 440 pc from
the Earth were inferred. On the other hand, spectroscopic analysis by
Dreizler & Heber (1998) yield
![]() K and
K and
![]() ,
in good agreement with the asteroseismic fit of KB94, but a higher
luminosity of
,
in good agreement with the asteroseismic fit of KB94, but a higher
luminosity of
![]() .
.
- PG 2131+066: discovered as a variable star
by Bond et al. (1984) with periods of about 414 and 386 s, along with
some other periodicities. On the basis of an augmented set of periods
from WET data, Kawaler et al. (1995) considered a
![]() K and obtained a precise mass determination of
K and obtained a precise mass determination of
![]() ,
a luminosity of
,
a luminosity of
![]() ,
and a distance from the
Earth of 470 pc. Spectroscopic constraints of Dreizler & Heber
(1998) give
,
and a distance from the
Earth of 470 pc. Spectroscopic constraints of Dreizler & Heber
(1998) give
![]() ,
,
![]() K,
K,
![]() ,
and
,
and
![]() for PG 2131+066. By using the updated
Dreizler & Heber (1998)'s determination of the effective temperature,
Reed et al. (2000) refined the procedure of Kawaler et al. (1995).
They found
for PG 2131+066. By using the updated
Dreizler & Heber (1998)'s determination of the effective temperature,
Reed et al. (2000) refined the procedure of Kawaler et al. (1995).
They found
![]() ,
a luminosity of
,
a luminosity of
![]() ,
and
a seismic distance to PG 2131+066 of 668 pc.
,
and
a seismic distance to PG 2131+066 of 668 pc.
- PG 1707+427: discovered to be a pulsator
by Bond et al. (1984). Dreizler & Heber (1998) obtained
![]() K and
K and
![]() ,
while a stellar mass and luminosity
of
,
while a stellar mass and luminosity
of
![]() and
and
![]() ,
respectively, were inferred
from their spectroscopic study. Recently, Kawaler et al. (2004)
report the analysis of multisite observations of PG 1707+427
obtained with WET. Preliminary model fits by using 7 independent
,
respectively, were inferred
from their spectroscopic study. Recently, Kawaler et al. (2004)
report the analysis of multisite observations of PG 1707+427
obtained with WET. Preliminary model fits by using 7 independent
![]() modes with periods between 334 and 910 ssuggest an
asteroseismic mass and luminosity of
modes with periods between 334 and 910 ssuggest an
asteroseismic mass and luminosity of
![]() and
and
![]() ,
respectively.
,
respectively.
- PG 0122+200: the coolest GW Vir variable with
![]() K and
K and
![]() (Dreizler & Heber
1998). Spectroscopy indicates a stellar mass of
(Dreizler & Heber
1998). Spectroscopy indicates a stellar mass of
![]() and
a gravity of
and
a gravity of
![]() .
By employing an analysis based on
multisite observations with WET, O'Brien et al. (1998) report a
seismic stellar mass of
.
By employing an analysis based on
multisite observations with WET, O'Brien et al. (1998) report a
seismic stellar mass of
![]() ,
strikingly higher than the
spectroscopic estimation. The cooling of PG 0122+200 appears to be
dominated by neutrino loses; this renders PG 0122+200 as the prime
target for learning neutrino physics (O'Brien et al. 1998).
,
strikingly higher than the
spectroscopic estimation. The cooling of PG 0122+200 appears to be
dominated by neutrino loses; this renders PG 0122+200 as the prime
target for learning neutrino physics (O'Brien et al. 1998).
We employ three different methods to infer the structural parameters
of these four GW Vir stars. First, we estimate the
stellar masses by using the asymptotic period spacing of our models
as computed from Eq. (4). More specifically, we
directly compare
![]() and the observed
mean period spacing
and the observed
mean period spacing
![]() ,
assuming that the
effective temperature of the target star is that obtained by means of
spectroscopy. In the second approach, we repeat this procedure but
this time using the average of the computed period spacings
,
assuming that the
effective temperature of the target star is that obtained by means of
spectroscopy. In the second approach, we repeat this procedure but
this time using the average of the computed period spacings
![]() and comparing it with the observed mean
period spacing
and comparing it with the observed mean
period spacing
![]() .
The third approach is a
fitting method in which we compare the theoretical (
.
The third approach is a
fitting method in which we compare the theoretical (
![]() )
and observed (
)
and observed (
![]() )
periods by means of a standard
)
periods by means of a standard ![]() algorithm. In the three approaches we assume that the observed periods
correspond to
algorithm. In the three approaches we assume that the observed periods
correspond to
![]() modes.
modes.
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{4199f-15.eps}
\end{figure}](/articles/aa/full/2006/30/aa4199-05/Timg190.gif) |
Figure 15:
The asymptotic period spacing for PG 1159 models with
stellar masses of
|
| Open with DEXTER | |
Table 1:
The values of the stellar mass (in ![]() )
from spectroscopic
and asteroseismic studies, and the values obtained in this work from three
different methods.
)
from spectroscopic
and asteroseismic studies, and the values obtained in this work from three
different methods.
We start by examining Fig. 15, in which the asymptotic
period spacing (
![]() )
is shown in terms of the
effective temperature for PG 1159 sequences with stellar masses of
)
is shown in terms of the
effective temperature for PG 1159 sequences with stellar masses of
![]() .
We also include in this figure the values
of the observed mean period spacing,
.
We also include in this figure the values
of the observed mean period spacing,
![]() ,
corresponding to the GW Vir stars PG 1159-035, PG 2131+066, PG 1707+427, and PG 0122+200. The values of
,
corresponding to the GW Vir stars PG 1159-035, PG 2131+066, PG 1707+427, and PG 0122+200. The values of
![]() and
the associated error bars are taken from Table 6 of Kawaler et al.
(2004). Table 1 summarizes our results. Note that the
spectroscopic estimation of
and
the associated error bars are taken from Table 6 of Kawaler et al.
(2004). Table 1 summarizes our results. Note that the
spectroscopic estimation of
![]() for PG 0122+200 places it at
an effective temperature that is lower than our PG 1159 models. Thus,
we can only make a rough extrapolation for PG 0122+200, but
there is a noticeable agreement between our estimates and the values in other pulsation studies. Note also that the seismic inferences
suggest higher mass values as compared with the spectroscopic
estimations. We do not actually understand the origin of this
discrepancy, but do note that spectroscopic derivations of the stellar
mass are usually very uncertain due to the large uncertainty in
determining
for PG 0122+200 places it at
an effective temperature that is lower than our PG 1159 models. Thus,
we can only make a rough extrapolation for PG 0122+200, but
there is a noticeable agreement between our estimates and the values in other pulsation studies. Note also that the seismic inferences
suggest higher mass values as compared with the spectroscopic
estimations. We do not actually understand the origin of this
discrepancy, but do note that spectroscopic derivations of the stellar
mass are usually very uncertain due to the large uncertainty in
determining ![]() ,
where an error of 0.3 dex translates into an
error of
,
where an error of 0.3 dex translates into an
error of
![]() (Dreizler & Heber 1998). Indeed, Dreizler
& Heber (1998) first estimate
(Dreizler & Heber 1998). Indeed, Dreizler
& Heber (1998) first estimate ![]() and
and
![]() values by
using fits to model atmospheres, and then they select the stellar mass
from the evolutionary tracks of O'Brien (2000). Thus, both the large
uncertainties in the estimation of
values by
using fits to model atmospheres, and then they select the stellar mass
from the evolutionary tracks of O'Brien (2000). Thus, both the large
uncertainties in the estimation of ![]() (
(![]() 0.5 dex) and in
the evolutionary computations could account for an excessively broad
range of allowed masses for a specific star.
0.5 dex) and in
the evolutionary computations could account for an excessively broad
range of allowed masses for a specific star.
After repeating the procedure described in Sect. 4.1, but using
the average of the computed period spacings
(
![]() )
instead the asymptotic period spacing,
we compared
)
instead the asymptotic period spacing,
we compared
![]() with the measured
with the measured
![]() for each star under consideration.
In these computations we only considered the period interval in which the periodicities of a given star were observed. For instance, for PG 1159-035, we computed the average of the computed period spacings for periods in the range [430, 841] s.
for each star under consideration.
In these computations we only considered the period interval in which the periodicities of a given star were observed. For instance, for PG 1159-035, we computed the average of the computed period spacings for periods in the range [430, 841] s.
The results of our calculations are shown in Fig. 16, in
which we show
![]() in terms of
in terms of
![]() for the four GW Vir stars. Since we perform the average of the computed period spacings on different period ranges according to
the period range exhibited by a specific star, the curves of
for the four GW Vir stars. Since we perform the average of the computed period spacings on different period ranges according to
the period range exhibited by a specific star, the curves of
![]() are different in each panel. In Table 1 we include the estimations of the stellar mass for the four stars. The stellar masses as determined by this approach are appreciably lower
than the values inferred by using the asymptotic period spacing and
thus in better agreement with spectroscopic inferences. This is due
to
are different in each panel. In Table 1 we include the estimations of the stellar mass for the four stars. The stellar masses as determined by this approach are appreciably lower
than the values inferred by using the asymptotic period spacing and
thus in better agreement with spectroscopic inferences. This is due
to
![]() being typically
being typically
![]() s
smaller than
s
smaller than
![]() ,
irrespective of the stellar
mass and effective temperature. Thus, if we compare the observed mean
period spacing for a given star with
,
irrespective of the stellar
mass and effective temperature. Thus, if we compare the observed mean
period spacing for a given star with
![]() ,
we obtain a lower total mass (
,
we obtain a lower total mass (
![]() lower)
than when comparing the observed mean period spacing with
lower)
than when comparing the observed mean period spacing with
![]() .
The asymptotic period
spacing
.
The asymptotic period
spacing
![]() ,
as computed by means of Eq. (4), is formally valid for the limit of high radial order k in chemically homogeneous stars. Because our PG 1159 models are
chemically stratified, we conclude that the estimations of M* from
,
as computed by means of Eq. (4), is formally valid for the limit of high radial order k in chemically homogeneous stars. Because our PG 1159 models are
chemically stratified, we conclude that the estimations of M* from
![]() are more realistic than those inferred by
means of
are more realistic than those inferred by
means of
![]() .
We also find that our M*values are lower than those quoted by other seismic studies (see Table 1). With the exception of the work of KB94 for PG 1159-035, all these studies compare the observed mean period spacing
with the asymptotic predictions to infer the stellar mass. Thus, not
surprisingly, their values are very similar to our results
from the asymptotic period spacing in
Sect. 4.1, but rather departed from our values deduced from
the average of the computed period spacings.
.
We also find that our M*values are lower than those quoted by other seismic studies (see Table 1). With the exception of the work of KB94 for PG 1159-035, all these studies compare the observed mean period spacing
with the asymptotic predictions to infer the stellar mass. Thus, not
surprisingly, their values are very similar to our results
from the asymptotic period spacing in
Sect. 4.1, but rather departed from our values deduced from
the average of the computed period spacings.
![\begin{figure}
\par\includegraphics[clip,width=8.4cm,clip]{4199f-16.eps}
\end{figure}](/articles/aa/full/2006/30/aa4199-05/Timg214.gif) |
Figure 16:
The average of the computed period spacings
for PG 1159 models with different stellar masses in terms of the
effective temperature. Each panel corresponds to a specific GW Vir
star. The observed mean period spacing
|
| Open with DEXTER | |
We turn now to the ![]() period fitting procedure. The goodness of
a given fit was measured by means of a quality function, defined as
period fitting procedure. The goodness of
a given fit was measured by means of a quality function, defined as
We initially searched the optimal model within a wide interval of
effective temperatures, ranging from the hottest point reached by the
model in the H-R diagram (
160 000-200 000 K, according to the
value of M*) until
![]() K. However,
throughout our calculations we realized that generally the run of
K. However,
throughout our calculations we realized that generally the run of ![]() as a function of
as a function of
![]() for a given star exhibits more
than one minimum, meaning that the period spectrum of the star could
not be fitted by a unique PG 1159 model. This behavior is more
pronounced in the case of the GW Vir stars with few observed periods
available. This effect can be understood on the basis that the
pulsation periods of a specific model generally increase with
time. If at a given effective temperature the model shows a close fit
to the observed periods, then the function
for a given star exhibits more
than one minimum, meaning that the period spectrum of the star could
not be fitted by a unique PG 1159 model. This behavior is more
pronounced in the case of the GW Vir stars with few observed periods
available. This effect can be understood on the basis that the
pulsation periods of a specific model generally increase with
time. If at a given effective temperature the model shows a close fit
to the observed periods, then the function ![]() reaches a local
minima. Later when the model has cooled enough, it is
possible that the accumulated period drift nearly matches the period
spacing between adjacent modes (
reaches a local
minima. Later when the model has cooled enough, it is
possible that the accumulated period drift nearly matches the period
spacing between adjacent modes (
![]() ). In these
circumstances, the model is able to fit the star again, as a result of
which
). In these
circumstances, the model is able to fit the star again, as a result of
which ![]() exhibits other local minimum. To break this
degeneracy, we decided to consider a more restricted range of
effective temperatures, but one that still comfortably embraces the
spectroscopic estimation of
exhibits other local minimum. To break this
degeneracy, we decided to consider a more restricted range of
effective temperatures, but one that still comfortably embraces the
spectroscopic estimation of
![]() and its uncertainties.
Specifically, in seeking the "best-fit'' model for a specific star,
we considered effective temperatures inside an interval
and its uncertainties.
Specifically, in seeking the "best-fit'' model for a specific star,
we considered effective temperatures inside an interval
![]() K, where
K, where
![]() is the spectroscopic
determination of the effective temperature. As described
below, for the star PG 1159-035 we were able to find a best-fit model
for which
is the spectroscopic
determination of the effective temperature. As described
below, for the star PG 1159-035 we were able to find a best-fit model
for which ![]() adopts the lowest value within this interval of
adopts the lowest value within this interval of
![]() s. The situation was considerably more difficult for PG 2131+066, PG 1707+427, and PG 0122+200, due to the scarcity of
pulsation periods characterizing their pulsation spectra. In fact,
the ambiguity associated to these stars with the existence of multiple
solutions persisted even when we adopted a more restricted
s. The situation was considerably more difficult for PG 2131+066, PG 1707+427, and PG 0122+200, due to the scarcity of
pulsation periods characterizing their pulsation spectra. In fact,
the ambiguity associated to these stars with the existence of multiple
solutions persisted even when we adopted a more restricted
![]() -interval, and in that case the procedure failed to isolate the
best solution. In order to solve this situation for PG 2131+066, PG 1707+427, and PG 0122+200, we restricted the search to within
-interval, and in that case the procedure failed to isolate the
best solution. In order to solve this situation for PG 2131+066, PG 1707+427, and PG 0122+200, we restricted the search to within ![]() of the spectroscopic value.
of the spectroscopic value.
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{4199f-17.eps}
\end{figure}](/articles/aa/full/2006/30/aa4199-05/Timg226.gif) |
Figure 17:
The |
| Open with DEXTER | |
We started by examining Fig. 17 in which the run of ![]() is plotted versus
is plotted versus
![]() for PG 1159-035 and includes
the results for the complete set of stellar masses considered in this
work. The periods observed were the same twenty
for PG 1159-035 and includes
the results for the complete set of stellar masses considered in this
work. The periods observed were the same twenty
![]() consecutive periods considered in KB94. The vertical dotted line
corresponds to the effective temperature of PG 1159-035 as measured by
means of spectroscopic techniques (
consecutive periods considered in KB94. The vertical dotted line
corresponds to the effective temperature of PG 1159-035 as measured by
means of spectroscopic techniques (
![]() K). Note that there is a well-defined minima of
K). Note that there is a well-defined minima of ![]() ,
corresponding to a stellar model with
,
corresponding to a stellar model with
![]() and
and
![]() K. We adopt this model
as our best-fit model. A comparison between the observed periods of
PG 1159-035 and the theoretical periods corresponding to the best-fit
model is included in Table 2. The first column lists the observed
periods, and the second and third columns correspond to the computed
periods and the associated radial order, respectively. The last two
columns show the difference and the relative difference (in percent)
between the observed and computed periods, respectively, defined as
K. We adopt this model
as our best-fit model. A comparison between the observed periods of
PG 1159-035 and the theoretical periods corresponding to the best-fit
model is included in Table 2. The first column lists the observed
periods, and the second and third columns correspond to the computed
periods and the associated radial order, respectively. The last two
columns show the difference and the relative difference (in percent)
between the observed and computed periods, respectively, defined as
![]() and
and
![]() .
Note that the period match
is excellent. To quantitatively measure the quality of the fit we
computed the mean of the period differences,
.
Note that the period match
is excellent. To quantitatively measure the quality of the fit we
computed the mean of the period differences,
![]() and the root-mean-square residual,
and the root-mean-square residual,
![]() .
We obtained
.
We obtained
![]() s and
s and
![]() s for
the fit to PG 1159-035. The quality of our fit is comparable to that
achieved by KB94 (
s for
the fit to PG 1159-035. The quality of our fit is comparable to that
achieved by KB94 (
![]() s), although the
KB94 fit is notoriously better.
s), although the
KB94 fit is notoriously better.
In this connection, it is interesting to note that these authors adopt
![]() and the surface composition as free adjustable parameters for the period fit, in addition to the stellar mass and the effective temperature. Therefore, they are able to make a finer
tuning of the observed period spectrum than our own. The structural parameters of our best-fit model are listed in Table 6, which shows
the rather nice agreement between our predictions and the structural properties of PG 1159-035 as inferred by other standard techniques. For instance, the effective temperature, luminosity, and the surface gravity of our best-fit
model are consistent at the
and the surface composition as free adjustable parameters for the period fit, in addition to the stellar mass and the effective temperature. Therefore, they are able to make a finer
tuning of the observed period spectrum than our own. The structural parameters of our best-fit model are listed in Table 6, which shows
the rather nice agreement between our predictions and the structural properties of PG 1159-035 as inferred by other standard techniques. For instance, the effective temperature, luminosity, and the surface gravity of our best-fit
model are consistent at the ![]() level with the spectroscopic
estimations of Dreizler & Heber (1998). In particular, the quality
function of our period fit naturally adopts a unique minimum value at
an effective temperature that is very close to the spectroscopic value (this
is not the case for the remaining GW Vir stars; see below).
The total mass of our model lies at
level with the spectroscopic
estimations of Dreizler & Heber (1998). In particular, the quality
function of our period fit naturally adopts a unique minimum value at
an effective temperature that is very close to the spectroscopic value (this
is not the case for the remaining GW Vir stars; see below).
The total mass of our model lies at
![]() above the
spectroscopic mass, although well within the allowed range (
above the
spectroscopic mass, although well within the allowed range (
![]() ). Spectroscopy
determines only
). Spectroscopy
determines only ![]() and
and
![]() ,
and then the value of the
stellar mass is assessed using evolutionary tracks that depend on
the complete evolution of the progenitors. Our
seismological mass is lower than the value obtained by KB94 by
employing the same set of observed pulsation periods.
,
and then the value of the
stellar mass is assessed using evolutionary tracks that depend on
the complete evolution of the progenitors. Our
seismological mass is lower than the value obtained by KB94 by
employing the same set of observed pulsation periods.
Table 2:
Comparison between the observed periods of
PG 1159-035 (taken from KB94) and the theoretical (![]() )
periods of the
best-fit model (
)
periods of the
best-fit model (
![]() s,
s,
![]() s).
s).
In contrast to PG 1159-035, the stars PG 2131+066, PG 1707+427, and
PG 0122+200 exhibit very few pulsation periods in their light
curves. As anticipated, this unfortunate fact makes any
asteroseismic inference on these stars much more difficult.
This is the reason for which most asteroseismic studies so
far rely only on the measured period spacing. In spite of this,
we attempted to apply the ![]() fitting method to these stars
by adopting a stricter criteria, i.e., by considering only those
solutions as valid that guaranteed consistency at
fitting method to these stars
by adopting a stricter criteria, i.e., by considering only those
solutions as valid that guaranteed consistency at ![]() level with the
spectroscopic determination of
level with the
spectroscopic determination of
![]() .
Figure 18
shows the results for PG 2131+066, for which the observational
data consists of only the seven pulsation periods reported by Kawaler
et al. (1995).
.
Figure 18
shows the results for PG 2131+066, for which the observational
data consists of only the seven pulsation periods reported by Kawaler
et al. (1995).
At variance with the case of PG 1159-035,
function ![]() shows various minima compatible with
shows various minima compatible with
![]() in the range of the effective temperatures considered.
For instance, for
in the range of the effective temperatures considered.
For instance, for
![]() there is a remarkable minimum
in the immediate vicinity of the spectroscopic estimation at
there is a remarkable minimum
in the immediate vicinity of the spectroscopic estimation at
![]() K. Other comparable minima of
K. Other comparable minima of ![]() are
seen also for stellar masses of
0.61, 0.63, and
are
seen also for stellar masses of
0.61, 0.63, and
![]() but
at effective temperatures that depart somewhat from the spectroscopic
value. These minima represent equivalent solutions from the point of
view of the magnitude of
but
at effective temperatures that depart somewhat from the spectroscopic
value. These minima represent equivalent solutions from the point of
view of the magnitude of ![]() ,
so there are various
possible optimal models. We adopt the model having the effective
temperature closer to the spectroscopic determination as the best-fit model, that is, the model with
,
so there are various
possible optimal models. We adopt the model having the effective
temperature closer to the spectroscopic determination as the best-fit model, that is, the model with
![]() and
and
![]() K (indicated with an arrow in
Fig. 18). A comparison between the observed periods of
PG 2131+066 and the theoretical (
K (indicated with an arrow in
Fig. 18). A comparison between the observed periods of
PG 2131+066 and the theoretical (![]() )
periods of the best-fit
model is given in Table 3. The overall quality of the fit
(
)
periods of the best-fit
model is given in Table 3. The overall quality of the fit
(
![]() s,
s,
![]() s) is
almost as satisfactory as in the case of PG 1159-035 (Table 2). The
characteristics of our best-fit model for PG 2131+066 are listed in
Table 6. Our results agree well with spectroscopy,
although our determination of the stellar mass is significantly higher,
but is even consistent at the
s) is
almost as satisfactory as in the case of PG 1159-035 (Table 2). The
characteristics of our best-fit model for PG 2131+066 are listed in
Table 6. Our results agree well with spectroscopy,
although our determination of the stellar mass is significantly higher,
but is even consistent at the ![]() level. The
disagreement in the estimation of the stellar mass would be more
pronounced if we were adopting any of the other acceptable
solutions, for which
level. The
disagreement in the estimation of the stellar mass would be more
pronounced if we were adopting any of the other acceptable
solutions, for which
![]() .
.
![\begin{figure}
\par\includegraphics[width=8.3cm,clip]{4199f-18.eps}
\end{figure}](/articles/aa/full/2006/30/aa4199-05/Timg244.gif) |
Figure 18: Same as Fig. 17, but for PG 2131+066. |
| Open with DEXTER | |
Table 3:
Comparison between the observed periods
of PG 2131+066 (taken from Kawaler et al. 1995)
and the theoretical (![]() )
periods of the
best-fit model (
)
periods of the
best-fit model (
![]() s,
s,
![]() s).
s).
Table 4:
Comparison between the observed periods
of PG 1707+427 (taken from Kawaler et al. 2004) and
the theoretical (![]() )
periods of the best-fit model
(
)
periods of the best-fit model
(
![]() s,
s,
![]() s).
s).
Table 5:
Comparison between the observed periods
of PG 0122+200 (taken from Vauclair et al. 2001) and the
theoretical (![]() )
periods of the best-fit model
(
)
periods of the best-fit model
(
![]() s,
s,
![]() s).
s).
Table 6:
Summary of the seismic inferences for PG 1159-035,
PG 2131+066, PG 1707+427 and PG 0122+200 from ![]() period fits.
The values of the observed mean period spacing were extracted from Table 6 of Kawaler et al. (2004).
period fits.
The values of the observed mean period spacing were extracted from Table 6 of Kawaler et al. (2004).
We also applied our fitting procedure to the GW Vir stars PG 1707+427 and PG 0122+200. We found that the behavior of ![]() in these cases is, not surprisingly, very similar to that shown by
Fig. 18 for PG 02131+066, because these stars also
exhibit a very reduced number of pulsation periods. Therefore, to
obtain optimal representative models we employ the same procedure as
in the case of PG 02131+066; i.e., we consider as valid those solutions
that are consistent at
in these cases is, not surprisingly, very similar to that shown by
Fig. 18 for PG 02131+066, because these stars also
exhibit a very reduced number of pulsation periods. Therefore, to
obtain optimal representative models we employ the same procedure as
in the case of PG 02131+066; i.e., we consider as valid those solutions
that are consistent at ![]() with the spectroscopically inferred
effective temperature. In this way we discard other possible solutions
at effective temperatures that do not match the spectroscopic
evidence. The results are summarized in Tables 4 and 5, respectively.
For PG 1707+427 the period match has a slightly lower
quality than for PG 1159-035 and PG 2131+066, but is still satisfactory
with
with the spectroscopically inferred
effective temperature. In this way we discard other possible solutions
at effective temperatures that do not match the spectroscopic
evidence. The results are summarized in Tables 4 and 5, respectively.
For PG 1707+427 the period match has a slightly lower
quality than for PG 1159-035 and PG 2131+066, but is still satisfactory
with
![]() s and
s and
![]() s. For PG 0122+200, however, the fit is considerably worse at
s. For PG 0122+200, however, the fit is considerably worse at
![]() s and
s and
![]() s.
s.
The main source of discrepancy comes from the existence of periods at 449.43 and 468.69 s. For PG 0122+200 we also considered the set of observed periods reported by O'Brien et al. (1998), which do not include the period at 468.69 s. The quality of the fit in that case does not improve significantly. The structural properties of the best-fit models for PG 1707+427 and PG 0122+200 are given in Table 6. For PG 1707+427 we found general agreement between our inferences and the spectroscopic values, in particular for the stellar mass. In the case of PG 0122+200, we found a total mass and a surface gravity far in excess of the spectroscopic evidence. This high mass value is in line with other seismic determinations and also with our own predictions based on the asymptotic period spacing and the average of the computed period spacings (see Table 1).
In addition to the structural properties of the GW Vir stars under
study, we inferred their seismic distance from the Earth. First, we
computed the bolometric magnitude from the luminosity of the best-fit
model by means of
![]() ,
with
,
with
![]() (Allen
1973). Next, we transformed the bolometric magnitude into the absolute
magnitude,
(Allen
1973). Next, we transformed the bolometric magnitude into the absolute
magnitude,
![]() ,
where
,
where ![]() is
the bolometric correction. Finally, we computed the seismic distance
according to
is
the bolometric correction. Finally, we computed the seismic distance
according to
![]() .
For PG 1159-035 (
.
For PG 1159-035 (
![]() )
we adopted a bolometric correction
of
)
we adopted a bolometric correction
of
![]() from KB94. Following Kawaler et al. (1995), we adopted
from KB94. Following Kawaler et al. (1995), we adopted
![]() for PG 2131+066 (
for PG 2131+066 (
![]() )
and PG 1707+427 (
)
and PG 1707+427 (
![]() ). Because the lack of an estimation of the bolometric correction for PG 0112+200, we were unable to
infer its seismic distance.
). Because the lack of an estimation of the bolometric correction for PG 0112+200, we were unable to
infer its seismic distance.
Our seismic distances are shown in Table 6. In addition, we included the
distances estimated by means of other techniques. We found good
agreement (within ![]() )
between our distances and the other
non-seismic estimations, although our values are characterized by
much smaller errors. Our results are also consistent with the
distances obtained seismologically by KB94 for PG 1159-035 (
)
between our distances and the other
non-seismic estimations, although our values are characterized by
much smaller errors. Our results are also consistent with the
distances obtained seismologically by KB94 for PG 1159-035 (
![]() pc) and Reed et al. (2000) for PG 2131+066 (
d=
668+78-83 pc).
pc) and Reed et al. (2000) for PG 2131+066 (
d=
668+78-83 pc).
In this paper we have studied some relevant aspects of the adiabatic pulsations of GW Vir stars in detail by using state-of-the-art evolutionary PG 1159 models recently presented by Althaus et al. (2005). As far as we are aware, this is the first time that the adiabatic pulsation properties of fully evolutionary post born-again PG 1159 models like the ones used in this work are assessed. We refer the interested reader to the paper by Gautschy et al. (2005) for details about their non-adiabatic pulsation properties.
We first explored the basic nature of the pulsation modes by employing
propagation diagrams and weight functions. In line with previous
works, our results suggest that for PG 1159 models at high luminosity
stages, the propagation diagrams are reminiscent of those of their
progenitors, red giant stars, characterized by high values of
the Brunt-Väisälä frequency in the central regions of the star.
As a result, pulsation g-modes - the only observed so far in GW Vir stars - are closely confined to the highly condensed core,
whereas p-modes are free to oscillate in more external regions. In
addition, we found that several modes exist that exhibit a
mixed nature, by behaving as p-modes in outer regions and like
g-modes in the deeper zones within the star. As the effective
temperature increases, these modes undergo several episodes of
avoided crossing. We found that pulsation periods generally decrease
with time, an effect attributable to the rapid contraction experienced
by the star in their incursion to the blue in the H-R diagram. During
this contraction stage, all the considered eigenmodes are characterized by
a negative temporal rate of period change. Once the models have passed their maximum effective temperature and settled onto the WD cooling
track, the Brunt-Väisälä frequency acquires a more familiar
shape typical of the WD pulsators. In this phase all the pulsation
periods increase with decreasing effective temperature, reflecting a
lowering of the magnitude of the Brunt-Väisälä frequency at the
core regions. At this stage, g-modes become envelope modes, and, as
indicated by the weight functions, the outer regions of the star are
the more relevant ones in establishing the periods. In contrast,
pulsation p-modes are almost confined to the degenerate core.
Since all the periods increase during this phase, so the rate
of period change for any pulsation mode must be positive. In
particular, the measured period change rate of the period at ![]() s in PG 1159-035 is positive (Costa et al. 1999), in agreement
with our findings. We have deferred a complete discussion of
the rate of period change of our PG 1159 models to a future work.
s in PG 1159-035 is positive (Costa et al. 1999), in agreement
with our findings. We have deferred a complete discussion of
the rate of period change of our PG 1159 models to a future work.
We next focused our attention on the evolutionary stages when the star has already entered its WD cooling track. For these phases we were able to obtain additional evolutionary sequences with several values of the stellar mass, allowing us to study the effects of M* and the effective temperature on the pulsation properties of our models. In particular, we examined the asymptotic behavior of the g-mode pulsations. In agreement with previous works, we found that the asymptotic period spacing increases with a decrease in the stellar mass and with an increment in the luminosity, although the dependence on the stellar mass is stronger. This makes the value of the period spacing observed in a given star a powerful indicator of the total mass.
Studying the mode-trapping properties of our models was another
relevant aim of the present work. In this connection, we have
demonstrated that the mode-trapping features characterizing our PG 1159
models are mostly produced by the shape of the O/C chemical profile at
the core, at least for the range of periods observed in GW Vir stars.
On the other hand, the outer chemical interface of O/C/He produces
negligible mode-trapping effects, except for the regime of short
periods in the pulsation spectrum. This conclusion is at odds with
previous results reported by KB94, who realized that the mode-trapping
properties of their PG 1159 models were fixed essentially by the outer
O/C/He transition region. We found that the origin of this
discrepancy rests on the differences in the input physics used to
build the background stellar models. Specifically, the main
difference is the presence of a much less pronounced chemical
transition in the outer parts of the C/O core of the KB94 models, as
compared with the rather abrupt chemical gradients at
![]() in our PG 1159 models. Another ingredient that contributes
to the discrepancy between our results and those of KB94 is the
thickness of the helium envelope. Indeed, since our models are
characterized by thick helium envelopes (
in our PG 1159 models. Another ingredient that contributes
to the discrepancy between our results and those of KB94 is the
thickness of the helium envelope. Indeed, since our models are
characterized by thick helium envelopes (
![]() ), the mode trapping effects caused by the O/C/He transition
region are much weaker than in the models of KB94.
), the mode trapping effects caused by the O/C/He transition
region are much weaker than in the models of KB94.
The structure of the core chemical profile of our PG 1159 models is the relic of convective overshoot episodes during the central helium-burning phase. The sensitivity of the mode-trapping effects to the details of the core chemical structure raises the possibility of employing pulsating PG 1159 and WD stars to constrain the efficiency of extra mixing episodes in the core of their progenitors (overshooting and/or semiconvection; see Straniero et al. 2003). This appealing issue has been recently explored by Córsico & Althaus (2005).
To gain additional insight into the nature of mode trapping in our models, we examined the kinetic energy and weight functions of individual pulsation modes, and found that modes showing primary maxima in the kinetic energy distribution are associated with minima in the period-spacing diagrams. By consulting the eigenfunctions and weight functions of these modes we found that they have relatively high amplitude in the high-density environment of the stellar core, and very low amplitudes in the rest of the star. The existence of these "core-trapped'' modes is also encountered in the context of ZZ Ceti pulsations, as reported by Althaus et al. (2003) and Córsico et al. (2005).
Finally, we made some preliminary seismic inferences about the internal structure and basic parameters of the GW Vir stars PG 1159-035, PG 2131+066, PG 1707+427, and PG 0122+200. To this end, we adopted three different approaches. First, we estimated the stellar masses by comparing the asymptotic period spacing with the observed mean period spacing and assuming that the effective temperature of the target star is what is predicted by spectroscopy. In the second method, we repeated the above procedure but using the average of the computed period spacings and comparing it with the observed mean period spacing. The third approach is a fitting method in which we search for the optimal stellar model that best reproduces the observed periods. To do this, we employed a quality function that measures the distance between the observed and the computed adiabatic pulsation periods within a grid of models with different effective temperatures and stellar masses.
The stellar masses we obtained from these methods are given in Table 1. Note that, except for PG 0122+200, our values are consistent with the inferences of the spectroscopy, particularly when the average of the computed period spacings are used, although our masses are slightly higher. For PG 0122+200, in agreement with the results of O'Brien (2000), we obtain a large value of the stellar mass. Thus, according the pulsation theory this star seems to be the most massive among the high-gravity GW Vir pulsators. Note also that the stellar masses determined by employing the average of the computed period spacings are appreciably lower than the values using the asymptotic period spacing. We also found that our M*values are lower than reported in other pulsation studies. In this connection, we note that all these works, with the exception of the work of KB94 for PG 1159-035, compare the observed mean period spacing with the asymptotic predictions to get the stellar mass. Thus, not surprisingly, their values are very close to our results from the asymptotic period spacing, but somewhat different from our values employing the average of the computed period spacings.
The results from our period-fitting procedure are shown in Table 6.
Taking full advantage of the numerous pulsation periods observed in PG 1159-035, we unambiguously obtained a best-fit model with an
effective temperature very close to what is predicted by spectroscopy.
Our asteroseismic mass of
![]() is consistent with the
spectroscopic calibration (
is consistent with the
spectroscopic calibration (
![]() )
and with the
preferred value of Gautschy et al. (2005) (
)
and with the
preferred value of Gautschy et al. (2005) (
![]() ),
but considerably lower than the value quoted by KB94 (
),
but considerably lower than the value quoted by KB94 (
![]() ). For the remaining stars, for which we have very few
observed periods available, we also obtained representative
models by employing our period-fitting procedure, but, in contrast to
the case of PG 1159-035, for these stars we have been forced to
consider as acceptable solutions only models with an effective
temperature lying within
). For the remaining stars, for which we have very few
observed periods available, we also obtained representative
models by employing our period-fitting procedure, but, in contrast to
the case of PG 1159-035, for these stars we have been forced to
consider as acceptable solutions only models with an effective
temperature lying within ![]() of the spectroscopic value. This
stringent criteria was necessary in view of the numerous and almost
equivalent minima exhibited by the quality function for these stars.
Note that the period matching is considerably poorer (Tables 3-5) compared with the case of PG 1159-035 (Table 2). We also
estimated the seismic distances to the stars by employing the
luminosity of the best-fit models. Our estimations (see Table 6) are
consistent with other determinations.
of the spectroscopic value. This
stringent criteria was necessary in view of the numerous and almost
equivalent minima exhibited by the quality function for these stars.
Note that the period matching is considerably poorer (Tables 3-5) compared with the case of PG 1159-035 (Table 2). We also
estimated the seismic distances to the stars by employing the
luminosity of the best-fit models. Our estimations (see Table 6) are
consistent with other determinations.
In our view, the pulsational analysis presented here constitutes a substantial improvement over previous studies. However, we believe that PG 1159 evolutionary models with different stellar masses based on a complete description of the physical processes occurring in all the evolutionary stages of progenitor stars would be needed to reinforce some of our results. The development of such models is certainly critical in assessing the internal chemical composition characterizing GW Vir stars, an issue that is key in precision asteroseismology.
Finally, the evolutionary tracks employed in this investigation, as
well as tabulations of ![]() in terms of L* and
in terms of L* and
![]() for
the complete set of stellar masses are freely available at our URL:
http://www.fcaglp.unlp.edu.ar/evolgroup/.
for
the complete set of stellar masses are freely available at our URL:
http://www.fcaglp.unlp.edu.ar/evolgroup/.
Acknowledgements
We wish to thank the anonymous referee for the suggestions and comments that improved the original version of this work. This research was supported by the Instituto de Astrofísica La Plata (CONICET).
Our numerical pulsation code solves the fourth-order set of
equations governing linear,
nonradial, adiabatic stellar pulsations in the formulation
given in Unno et al. (1989):
![\begin{displaymath}x \frac{{\rm d}y_1}{{\rm d}r}= \left(V_g-3\right)\ y_1 + \lef...
...ac{\ell(\ell+1)}
{C_1 \omega^2} - V_g \right]\ y_2 + V_g\ y_3,
\end{displaymath}](/articles/aa/full/2006/30/aa4199-05/img278.gif) |
(A.1) |
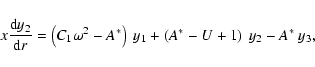 |
(A.2) |
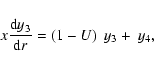 |
(A.3) |
![\begin{displaymath}x \frac{{\rm d}y_4}{{\rm d}r}\!=\! U A^*\ y_1 + U V_g\ y_2 +
\left[ \ell(\ell+1) - U V_g\right]\ y_3 - U\ y_4.
\end{displaymath}](/articles/aa/full/2006/30/aa4199-05/img281.gif) |
(A.4) |
The boundary conditions are, at the stellar center (x=0):
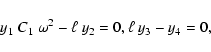 |
(A.5) |
and at the stellar surface (x=1):
| (A.6) |
being the normalization y1= 1 at x=1 (x=r/R*). The dimensionless Dziembowski's variables (eigenvalue and eigenfunctions) are defined as
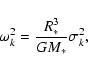 |
(A.7) |
and
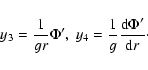 |
(A.9) |
Here, ![]() is the radial Lagrangian
displacement, and p',
is the radial Lagrangian
displacement, and p', ![]() are the Eulerian perturbation of
the pressure and the gravitational potential, respectively. Pertinent
dimensionless coefficients of the pulsation equations are:
are the Eulerian perturbation of
the pressure and the gravitational potential, respectively. Pertinent
dimensionless coefficients of the pulsation equations are:
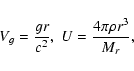 |
(A.10) |
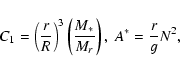 |
(A.11) |
where c is the adiabatic local sound speed and N
the Brunt-Väisälä frequency. The remaining symbols are
self-explanatory. Once the eigenvalue and eigenfunctions are computed,
the code proceeds to evaluate a number of important pulsation
quantities, such as the pulsation period, ![]() ,
,
| (A.12) |
the oscillation kinetic energy, Kk,
the weight function, Wk,
![\begin{displaymath}\Pi_{k}^v= \sqrt{\frac{8 \pi^2}{G M_*}}\
\frac{K_{k}^{1/2}}{\omega_{k}} \left[
\int_0^1 W_k(x)\ x^2 {\rm d}x \right]^{-1/2},
\end{displaymath}](/articles/aa/full/2006/30/aa4199-05/img295.gif) |
(A.15) |
and finally, the first-order rotation splitting coefficients, Ck,
![\begin{displaymath}C_{k}= \frac{(G M_* R_*^2)}{2 K_{k}}
\int_{0}^{1}
\frac{x^2 ...
... y_1 y_2 + \frac{x^2}{C_1 \omega_{k}^2}
y_2^2\right] {\rm d}x.
\end{displaymath}](/articles/aa/full/2006/30/aa4199-05/img296.gif) |
(A.16) |
| (A.17) |
where ![]() is the angular speed of rotation and mthe azimutal quantum number.
is the angular speed of rotation and mthe azimutal quantum number.