Astrometric accuracy of complex modern VLBI arrays cannot be calculated analytically. We study the astrometric accuracy of phase-referenced VLBI observations for the VLBA, EVN and global VLBI array by simulating VLBI data for targets at declinations
A&A 452, 1099-1106 (2006)
DOI: 10.1051/0004-6361:20053021
N. Pradel1 - P. Charlot1 - J.-F. Lestrade2
1 - Observatoire de Bordeaux (OASU) - CNRS/UMR
5804, BP 89, 33270 Floirac, France
2 - Observatoire de Paris - CNRS/UMR 8112, 61 avenue de
l'Observatoire, 75014 Paris, France
Received 8 March 2005 / Accepted 4 January 2006
Abstract
Astrometric accuracy of complex modern VLBI arrays cannot
be calculated analytically. We study the astrometric accuracy of
phase-referenced VLBI observations for the VLBA, EVN and global VLBI
array by simulating VLBI data for targets at declinations
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() and
and
![]() .
The systematic
error components considered in this study are calibrator position,
station coordinate, Earth orientation and troposphere parameter
uncertainties. We provide complete tables of the astrometric
accuracies of these arrays for a source separation of
.
The systematic
error components considered in this study are calibrator position,
station coordinate, Earth orientation and troposphere parameter
uncertainties. We provide complete tables of the astrometric
accuracies of these arrays for a source separation of
![]() either
along the right ascension axis or along the declination
axis. Astrometric accuracy is
either
along the right ascension axis or along the declination
axis. Astrometric accuracy is ![]() as at mid declination and is
as at mid declination and is
![]() as at low (
as at low (
![]() )
and high (
)
and high (
![]() )
declinations
for the VLBA and EVN. In extending our simulations to source
separations of
)
declinations
for the VLBA and EVN. In extending our simulations to source
separations of
![]() and
and
![]() ,
we establish the formula for
the astrometric accuracy of the VLBA:
,
we establish the formula for
the astrometric accuracy of the VLBA:
![]() (
(![]() as) where
as) where
![]() is the astrometric accuracy for a separation
is the astrometric accuracy for a separation
![]() provided in our tables for various declinations and
conditions of the wet troposphere. We argue that this formula is also
valid for the astrometric accuracy of the EVN and global VLBI array.
provided in our tables for various declinations and
conditions of the wet troposphere. We argue that this formula is also
valid for the astrometric accuracy of the EVN and global VLBI array.
Key words: astrometry - techniques: high angular resolution - techniques: interferometric
Very Long Baseline Interferometry (VLBI) narrow-angle astrometry pioneered by Shapiro et al. (1979) makes use of observations of pairs of angularly close sources to cancel atmospheric phase fluctuations between the two close lines of sight. In this initial approach, the relative coordinates between the two strong quasars 3C 345 and NRAO512 and other ancilliary parameters were adjusted by a least-squares fit of the differenced phases after connecting the VLBI phases for both sources over a multi-hour experiment. Then, Marcaide & Shapiro (1984,1983) made the first phase-referenced map where structure and astrometry were disentangled for the double quasar 1038+528 A and B. Both of these experiments demonstrated formal errors at the level of a few tens of microarcseconds or less in the relative angular separation between the two sources.
Another approach was designed to tackle faint target sources by
observing a strong reference source (quasar) to increase the
integration time of VLBI from a few minutes to a few hours
(Lestrade et al. 1990). This approach improves the sensitivity by the factor
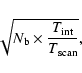
In the approach above, the VLBI phases of the strong reference source are connected, interpolated in time and differenced with the VLBI phases of the faint source that do not need to be connected. The differenced visibilities are then inverted to produce the map of the brightness distribution of the faint target source and its position is determined by reading directly the coordinates of the map peak which are relative to the a priori reference source coordinates. The map is usually highly undersampled but suffices for astrometry. This mapping astrometry technique is implemented in the SPRINT software (Lestrade et al. 1990) and a similar procedure is also used within the NRAO AIPS package to produce phase-referenced VLBI maps with absolute source coordinates on the sky.
While phase-referencing in this way is efficient, it still provides no direct positional uncertainty as does least-squares fitting of differenced phases (Shapiro et al. 1979). In order to circumvent this problem, we have developed simulations to evaluate the impact of systematic errors in the derived astrometric results. Such simulations have been carried out for of a pair of sources observed with the Very Long Baseline Array (VLBA) and the European VLBI Network (EVN) at various declinations and angular separations. Systematic errors in station coordinates, Earth rotation parameters, reference source coordinates and tropospheric zenith delays were studied in turn. The results of the simulations are summarized below in tables that indicate positional uncertainties when considering these systematic errors either separately or altogether. Such tables can be further interpolated to determine the accuracy of any full-track experiment with the VLBA and EVN.
Our study includes atmospheric fluctuations caused by the turbulent
atmosphere above all stations. These fluctuations have been considered
uniform and equivalent to a delay rate noise of 0.1 ps/s for all
stations. The impact of these fluctuations is limited if the antenna
switching cycle between the two sources is fast enough. The phase
structure function measured at 22 GHz above the VLA by Carilli & Holdaway (1999)
provides prescriptions on this switching time. At high frequency, it
can be as short as 10 s, as e.g. in Reid et al. (2003) who carried out
precise 43 GHz VLBA astrometric observations of Sgr A* at a
declination of
![]() .
Switching time in more clement conditions
is typically a few minutes at 8.4 GHz for northern sources.
.
Switching time in more clement conditions
is typically a few minutes at 8.4 GHz for northern sources.
A few applications of mapping astrometry are the search for extra-solar planets around radio-emitting stars (Lestrade et al. 1994), the determination of the Gravity Probe B guide star proper motion (Lebach et al. 1999), the determination of absolute motions of VLBI components in extragalactic sources, e.g. in compact symetric objects (Charlot et al. 2005) or core-jet sources (Ros et al. 1999), probing the jet collimation region in extragalactic nuclei (Ly et al. 2004), pulsar parallax and proper motion measurements (Brisken et al. 2002) and the determination of parallaxes and proper motions of maser sources in the whole Galaxy as planned with the VERA project (Honma et al. 2000; Kawaguchi et al. 2000).
As indicated in e.g. Thompson et al. (1986), the theoretical precision of
astrometry with the interferometer phase is
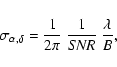 |
(1) |
While the theoretical precision above might be regarded as the potential accuracy attainable for the VLBI, systematic errors in the model of the phase limit narrow-angle astrometry precision to roughly ten times this level in practice (Fomalont et al. 1999). An analytical study of systematic errors in phase-referenced VLBI astrometry over a single baseline is given in Shapiro et al. (1979) and it shows that all systematic errors are scaled by the source separation. Another error analysis in such differential VLBI measurements can be found in Morabito (1984). However, for modern VLBI arrays with 10 or more antennae, the complex geometry makes the analytical approach intractable. For this reason, we have estimated such systematic errors by simulating VLBI visibilities and inverting them for a range of model parameters (station coordinates, reference source coordinates, Earth Orientation parameters, and tropospheric dry and wet zenith delays) corresponding to the expected errors in these parameters.
The visibilities were simulated for a pair of sources at declinations
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() and
with angular separations
and
with angular separations
![]() ,
,
![]() and 2
and 2
![]() for the
VLBA, EVN and global VLBI array (VLBA+EVN). For each of these cases,
we simulated visibilities every 2.5 min from source rise to set
(full track) with a lower limit on elevation of 7
for the
VLBA, EVN and global VLBI array (VLBA+EVN). For each of these cases,
we simulated visibilities every 2.5 min from source rise to set
(full track) with a lower limit on elevation of 7
![]() .
The adopted
flux for each source (calibrator and target) was 1 Jy to make the phase
thermal noise negligeable in our simulations. For applications to faint
target sources, one should combine the corresponding thermal astrometric
uncertainty (Eq. (1)) with the systematic errors derived below. The
simulated visibilities were then inverted using uniform weighting to
produce a phase-referenced map of the target source and estimate
its position. This operation was repeated 100 times in a Monte
Carlo analysis after varying slightly the parameters of the model
based on errors drawn from a Gaussian distribution with zero-mean and
plausible standard deviation. We report the rms of the differences
found between the known a priori position of the target source and the
resulting estimated positions as a measure of the corresponding systematic
errors for each of the above cases. We have adopted the usual
astrometric frequency of 8.4 GHz for this analysis.
.
The adopted
flux for each source (calibrator and target) was 1 Jy to make the phase
thermal noise negligeable in our simulations. For applications to faint
target sources, one should combine the corresponding thermal astrometric
uncertainty (Eq. (1)) with the systematic errors derived below. The
simulated visibilities were then inverted using uniform weighting to
produce a phase-referenced map of the target source and estimate
its position. This operation was repeated 100 times in a Monte
Carlo analysis after varying slightly the parameters of the model
based on errors drawn from a Gaussian distribution with zero-mean and
plausible standard deviation. We report the rms of the differences
found between the known a priori position of the target source and the
resulting estimated positions as a measure of the corresponding systematic
errors for each of the above cases. We have adopted the usual
astrometric frequency of 8.4 GHz for this analysis.
The phase delay and group delay in VLBI are described in
Sovers et al. (1998). The phase
![]() at frequency
at frequency ![]() is
related to the interferometer delay
is
related to the interferometer delay
![\begin{displaymath}\tau_{\rm g} = { { { [P][N][{\it EOP}]} { \vec b \cdot \vec k
\over c }}} \end{displaymath}](/articles/aa/full/2006/24/aa3021-05/img44.gif)
The model above is that implemented in the SPRINT software used for our simulations. It is thought to be complete for narrow-angle astrometry and additional refinements, such as ocean loading, atmospheric loading, etc., would not make difference into our results. We have not studied the ionosphere contribution to systematic errors. The unpredictible nature of the ionosphere makes this task difficult. Calibration of the ionosphere by dual-frequency observations, or over a wide bandwidth at low frequency (Brisken et al. 2002), or simply by observing at high frequency (>10 GHz) where the effect is small, offers solutions to this problem.
Table 1: Adopted rms errors for the source coordinates, VLBA station coordinates and Earth Orientation Parameters in our Monte Carlo simulations.
Table 2:
Dry and wet tropospheric zenith path delays (
![]() and
and
![]() )
at the VLBA stations along with the adopted rms
errors
)
at the VLBA stations along with the adopted rms
errors
![]() and
and
![]() in our Monte
Carlo simulations.
in our Monte
Carlo simulations.
The parameter rms errors adopted as plausible for the VLBA phase model
are listed in Tables 1 and 2. The reference
source coordinate uncertainties (
![]() ,
,
![]() )
of 1 mas are typical of those in the VLBA Calibrator
Survey (Beasley et al. 2002), from which most of the reference sources
originate. However, ICRF extragalactic sources have better position
accuracies down to 0.25 mas (Ma et al. 1998). We have thus carried
out the calculations for both of these cases (1 mas and 0.25 mas)
and both
)
of 1 mas are typical of those in the VLBA Calibrator
Survey (Beasley et al. 2002), from which most of the reference sources
originate. However, ICRF extragalactic sources have better position
accuracies down to 0.25 mas (Ma et al. 1998). We have thus carried
out the calculations for both of these cases (1 mas and 0.25 mas)
and both ![]() and
and ![]() have been perturbed by these
uncertainties in our simulations. The uncertainties for the station
coordinates are from the ITRF2000 frame (Boucher et al. 2004) while those
for the Earth Orientation Parameters are from the IERS web
site
have been perturbed by these
uncertainties in our simulations. The uncertainties for the station
coordinates are from the ITRF2000 frame (Boucher et al. 2004) while those
for the Earth Orientation Parameters are from the IERS web
site![]() . The adopted dry tropospheric rms error
. The adopted dry tropospheric rms error
![]() of 0.5 cm corresponds to 2.5 millibars in atmospheric
pressure uncertainty at sea level. Although barometer reading is
usually better, the absolute calibration of station barometers is at
this level. Uncertainties in the wet tropospheric zenith delay
of 0.5 cm corresponds to 2.5 millibars in atmospheric
pressure uncertainty at sea level. Although barometer reading is
usually better, the absolute calibration of station barometers is at
this level. Uncertainties in the wet tropospheric zenith delay
![]() derived from temperature and humidity are known to be
large (Saastamoinen 1973). Experience makes us believe that a 30% error is likely on
derived from temperature and humidity are known to be
large (Saastamoinen 1973). Experience makes us believe that a 30% error is likely on
![]() and thus we took 1/3 of
and thus we took 1/3 of
![]() as the plausible rms error
as the plausible rms error
![]() with a minimum value of 2 cm. We carried out
simulations for both mean and maximum values of wet zenith path delays
based on estimates of
with a minimum value of 2 cm. We carried out
simulations for both mean and maximum values of wet zenith path delays
based on estimates of
![]() recently derived from multiple
VLBA geodetic and astrometric sessions (Sovers 2003). The maximum wet
zenith delays and corresponding errors were used to investigate the
impact of extreme weather conditions on observations. These values are
listed for each VLBA station in Table 2.
recently derived from multiple
VLBA geodetic and astrometric sessions (Sovers 2003). The maximum wet
zenith delays and corresponding errors were used to investigate the
impact of extreme weather conditions on observations. These values are
listed for each VLBA station in Table 2.
Table 3:
VLBA rms astrometric errors (in ![]() as) for a relative source
separation
as) for a relative source
separation
![]() .
Individual astrometric error contributions
from calibrator position, Earth orientation parameter, station coordinate, and
dry and wet troposphere uncertainties are given separately, while the last
two lines indicate the total astrometric errors when all model parameters
are perturbed together.
.
Individual astrometric error contributions
from calibrator position, Earth orientation parameter, station coordinate, and
dry and wet troposphere uncertainties are given separately, while the last
two lines indicate the total astrometric errors when all model parameters
are perturbed together.
Table 4:
VLBA rms astrometric errors (in ![]() as) for a relative source
separation
as) for a relative source
separation
![]() .
Individual astrometric error contributions
from calibrator position, Earth orientation parameter, station coordinate, and
dry and wet troposphere uncertainties are given separately, while the last
two lines indicate the total astrometric errors when all model parameters
are perturbed together.
.
Individual astrometric error contributions
from calibrator position, Earth orientation parameter, station coordinate, and
dry and wet troposphere uncertainties are given separately, while the last
two lines indicate the total astrometric errors when all model parameters
are perturbed together.
We simulated the visibilities of a full u-v track experiment with the
VLBA for six declinations between
![]() and
and
![]() with a
with a
![]() relative source separation (either oriented in
right ascension or in declination). Uniform weighting was applied
to the visibilities, resulting in a synthesized beam mainly shaped by the
longest baselines. As a test, we have also removed the 9 baselines
smaller than 1500 km in length out of the 45 baseline array and
noted a decrease in systematic errors of
relative source separation (either oriented in
right ascension or in declination). Uniform weighting was applied
to the visibilities, resulting in a synthesized beam mainly shaped by the
longest baselines. As a test, we have also removed the 9 baselines
smaller than 1500 km in length out of the 45 baseline array and
noted a decrease in systematic errors of
![]() in a few test cases. Conservatively, we have retained these "short''
baselines in our final simulations. This is motivated by the fact that all
possible baselines must be kept for sensitivity when observing weak sources.
The antenna switching cycle
between target and reference sources was set to 2.5 min. The results,
however, do not depend critically on this value. It was chosen so
that the automatic phase connection routine for the reference source
does not discard too much data in the presence of a delay rate error of
0.1 ps/s (adopted uniformly for all the stations in the
simulation). As mentioned previously, we analysed these data simulated
with SPRINT using the a priori parameter values perturbed by some
errors. We carried out this analysis 100 times for each systematic error
component with perturbation errors drawn from Gaussian distributions
with zero mean and standard deviations according to the rms errors in
Tables 1 and 2. The resulting position of the
target was estimated by reading the peak position in each of the 100
phase-referenced maps. The pixel size in the maps was
0.05 mas. This size is small compared to the synthesized beam (
in a few test cases. Conservatively, we have retained these "short''
baselines in our final simulations. This is motivated by the fact that all
possible baselines must be kept for sensitivity when observing weak sources.
The antenna switching cycle
between target and reference sources was set to 2.5 min. The results,
however, do not depend critically on this value. It was chosen so
that the automatic phase connection routine for the reference source
does not discard too much data in the presence of a delay rate error of
0.1 ps/s (adopted uniformly for all the stations in the
simulation). As mentioned previously, we analysed these data simulated
with SPRINT using the a priori parameter values perturbed by some
errors. We carried out this analysis 100 times for each systematic error
component with perturbation errors drawn from Gaussian distributions
with zero mean and standard deviations according to the rms errors in
Tables 1 and 2. The resulting position of the
target was estimated by reading the peak position in each of the 100
phase-referenced maps. The pixel size in the maps was
0.05 mas. This size is small compared to the synthesized beam (![]() 1 mas
at 8.4 GHz on 8000 km baseline) and, hence, the uncertainty in the peak
position due to the pixel size is negligeable. This position was
determined by fitting a parabola over the full half beam width. This
procedure was used in the Hipparcos/VLBI work of Lestrade et al. (1999) and was
found to be appropriate. As expected, each position was slightly
offset from the map phase center, reflecting the corresponding
systematic errors. After substracting the initial perturbation in
the calibrator position, we calculated the rms of these 100 relative
coordinate offsets
1 mas
at 8.4 GHz on 8000 km baseline) and, hence, the uncertainty in the peak
position due to the pixel size is negligeable. This position was
determined by fitting a parabola over the full half beam width. This
procedure was used in the Hipparcos/VLBI work of Lestrade et al. (1999) and was
found to be appropriate. As expected, each position was slightly
offset from the map phase center, reflecting the corresponding
systematic errors. After substracting the initial perturbation in
the calibrator position, we calculated the rms of these 100 relative
coordinate offsets
![]() and
and
![]() for the adopted
for the adopted
![]() source separation in right ascension or declination. Note
that the mean of these 100 coordinate offsets was close to zero in all
cases. In Tables 3 and 4, we report the rms
astrometric errors for each individual error component along with
the total astrometric errors when all model parameters are perturbed
together in the simulation. The total errors were derived
by considering a 1 mas error in the calibration position.
source separation in right ascension or declination. Note
that the mean of these 100 coordinate offsets was close to zero in all
cases. In Tables 3 and 4, we report the rms
astrometric errors for each individual error component along with
the total astrometric errors when all model parameters are perturbed
together in the simulation. The total errors were derived
by considering a 1 mas error in the calibration position.
The wet troposphere systematic error clearly dominates over all the
other error components for
![]() but the calibrator
error dominates at higher declinations if its position is not known
to better than 1 mas.
This behavior was first noted by Shapiro et al. (1979) who derived analytical
formulae providing the astrometric errors caused by the calibrator coordinate
uncertainties in the case of a single VLBI baseline. A detailed analysis
comparing our simulated errors with those obtained from these formulae
is given in Appendix A. Other systematic errors,
in particular the Earth orientation parameter and the station
coordinate errors, are small. In Tables 3 and 4,
we note that astrometric errors originating from mean and maximum wet
troposphere uncertainties are not drastically different (a ratio of 1.5
at most).
but the calibrator
error dominates at higher declinations if its position is not known
to better than 1 mas.
This behavior was first noted by Shapiro et al. (1979) who derived analytical
formulae providing the astrometric errors caused by the calibrator coordinate
uncertainties in the case of a single VLBI baseline. A detailed analysis
comparing our simulated errors with those obtained from these formulae
is given in Appendix A. Other systematic errors,
in particular the Earth orientation parameter and the station
coordinate errors, are small. In Tables 3 and 4,
we note that astrometric errors originating from mean and maximum wet
troposphere uncertainties are not drastically different (a ratio of 1.5
at most).
![\begin{figure}
\par\includegraphics[angle=-90,width=9cm,clip]{3021fig1.ps}
\end{figure}](/articles/aa/full/2006/24/aa3021-05/Timg69.gif) |
Figure 1:
Distribution of total astrometric errors for a
|
| Open with DEXTER | |
Finally, we have plotted in Fig 1 the distribution of all
coordinate offsets
![]() and
and
![]() for
the
for
the
![]() declination target when all perturbation errors are
present. For this specific case we have carried out 1000 simulations to
refine the binning of the distribution. We have also performed the
Pearson test on all distributions and provide the reduced chi-square
declination target when all perturbation errors are
present. For this specific case we have carried out 1000 simulations to
refine the binning of the distribution. We have also performed the
Pearson test on all distributions and provide the reduced chi-square
![]() and probability p that such distributions are Gaussian
in Table 5. The results of this test show that most of the
distributions are not Gaussian with p generally smaller than 0.4.
and probability p that such distributions are Gaussian
in Table 5. The results of this test show that most of the
distributions are not Gaussian with p generally smaller than 0.4.
We have carried out a similar study for the EVN by simulating full track observations for the 10 stations of the array at 8.4 GHz. The adopted errors for the reference source coordinates and Earth orientation parameters were identical to those used in the VLBA simulations. Station coordinate errors were similar to the VLBA ones (1-6 mm), with the exception of those for Westerbork which are at the level of 50 mm (Charlot et al. 2002). The same scheme as that adopted for the VLBA was used to define zenith dry and wet tropospheric delay errors at each EVN station and the corresponding values are given in Table 6.
Table 5:
Reduced chi-square
![]() and probability p of Gaussian distribution
for the astrometric errors
and probability p of Gaussian distribution
for the astrometric errors
![]() and
and
![]() using the Pearson test.
using the Pearson test.
Since the EVN comprises antennas with different sensitivities, each
baseline has been weighted by the reciprocal of their noise
power equivalent
![]() with System
Equivalent Flux Densities (SEFDi) for each station according to
Table 2 of the EVN Status
Table
with System
Equivalent Flux Densities (SEFDi) for each station according to
Table 2 of the EVN Status
Table![]() (as
available in May 2003). The Effelsberg-Westerbork baseline is
the most sensitive baseline of the array but also the shortest one and
so unfavorable for high-accuracy astrometry. For this reason, we
decided to perform the simulations without this baseline, hence using
an array of 44 baselines only. We have applied uniform weighting to
the visibilities similarly to the VLBA. We have tested that in removing
the 12 baselines shorter than 1500 km in this 44 baseline array,
systematic errors decrease by
(as
available in May 2003). The Effelsberg-Westerbork baseline is
the most sensitive baseline of the array but also the shortest one and
so unfavorable for high-accuracy astrometry. For this reason, we
decided to perform the simulations without this baseline, hence using
an array of 44 baselines only. We have applied uniform weighting to
the visibilities similarly to the VLBA. We have tested that in removing
the 12 baselines shorter than 1500 km in this 44 baseline array,
systematic errors decrease by
![]() but, conservatively, we have kept them
in our simulations. In order to reduce the number of simulations,
calculations were carried out for only mean values of the wet zenith
tropospheric delays since the results when using mean or maximum
values were not found to be drasticaly different. We also did not
calculate individual contributions from calibrator
position, dry tropospheric zenith delay and Earth orientation parameter
errors since these were found to be very small for the VLBA (see
Tables 3 and 4). One should keep in mind, however,
that calibrator error dominates at high declination. The results
of the EVN simulations are reported in Tables 7 and 8
for a
but, conservatively, we have kept them
in our simulations. In order to reduce the number of simulations,
calculations were carried out for only mean values of the wet zenith
tropospheric delays since the results when using mean or maximum
values were not found to be drasticaly different. We also did not
calculate individual contributions from calibrator
position, dry tropospheric zenith delay and Earth orientation parameter
errors since these were found to be very small for the VLBA (see
Tables 3 and 4). One should keep in mind, however,
that calibrator error dominates at high declination. The results
of the EVN simulations are reported in Tables 7 and 8
for a
![]() source separation in right ascension or declination.
source separation in right ascension or declination.
At declination
![]() ,
many SPRINT maps were found to be
ambiguous, i.e. the main lobe of the point spread function of the EVN
could not be identified because secondary lobes were too
high. This is essentially caused by the relatively high latitude of
the array and hence to the difficulty of observing such low declination
sources due to very limited visibility periods. For this reason, we do
not provide EVN results for this declination. For other declinations,
EVN astrometric errors (Tables 7 and 8) are similar
to those found for the VLBA (Tables 3 and 4) and
the Westerbork position error is not a limiting factor. Declination
accuracies are somewhat better for the EVN than
for the VLBA at low declination (
,
many SPRINT maps were found to be
ambiguous, i.e. the main lobe of the point spread function of the EVN
could not be identified because secondary lobes were too
high. This is essentially caused by the relatively high latitude of
the array and hence to the difficulty of observing such low declination
sources due to very limited visibility periods. For this reason, we do
not provide EVN results for this declination. For other declinations,
EVN astrometric errors (Tables 7 and 8) are similar
to those found for the VLBA (Tables 3 and 4) and
the Westerbork position error is not a limiting factor. Declination
accuracies are somewhat better for the EVN than
for the VLBA at low declination (
![]() and
and
![]() ), a consequence of
the participation of Hartebeeshoek (South Africa) in such observations.
), a consequence of
the participation of Hartebeeshoek (South Africa) in such observations.
Table 6:
Dry and wet tropospheric zenith path delays (
![]() and
and
![]() )
at the EVN stations along with the adopted rms
errors
)
at the EVN stations along with the adopted rms
errors
![]() and
and
![]() in our Monte
Carlo simulations.
in our Monte
Carlo simulations.
Table 7:
EVN rms astrometric errors (in ![]() as) for a relative source separation
as) for a relative source separation
![]() .
Individual astrometric error contributions from station
coordinate and wet troposphere uncertainties are given separately along with the
total astrometric errors when all model parameters are perturbed together.
.
Individual astrometric error contributions from station
coordinate and wet troposphere uncertainties are given separately along with the
total astrometric errors when all model parameters are perturbed together.
Table 8:
EVN rms astrometric errors (in ![]() as) for a relative source separation
as) for a relative source separation
![]() .
Individual astrometric error contributions from station
coordinate and wet troposphere uncertainties are given separately along with the
total astrometric errors when all model parameters are perturbed together.
.
Individual astrometric error contributions from station
coordinate and wet troposphere uncertainties are given separately along with the
total astrometric errors when all model parameters are perturbed together.
Table 9:
Global VLBI array rms astrometric errors (in ![]() as) for a relative source separation
as) for a relative source separation
![]() .
The individual astrometric error contribution from wet troposphere
uncertainties is given separately along with the total astrometric errors when all
model parameters are perturbed together.
.
The individual astrometric error contribution from wet troposphere
uncertainties is given separately along with the total astrometric errors when all
model parameters are perturbed together.
Table 10:
Global VLBI array rms astrometric errors (in ![]() as) for a relative source separation
as) for a relative source separation
![]() .
The individual astrometric error contribution from wet troposphere
uncertainties is given separately along with the total astrometric errors when all
model parameters are perturbed together.
.
The individual astrometric error contribution from wet troposphere
uncertainties is given separately along with the total astrometric errors when all
model parameters are perturbed together.
Table 11:
VLBA without Saint Croix rms astrometric errors (in ![]() as) for a relative source separation
as) for a relative source separation
![]() .
The individual astrometric error contribution from wet troposphere
uncertainties is given separately along with the total astrometric errors when all
model parameters are perturbed together.
.
The individual astrometric error contribution from wet troposphere
uncertainties is given separately along with the total astrometric errors when all
model parameters are perturbed together.
We have carried out a similar study for the global VLBI array which is the combination of the VLBA and EVN. It includes 20 stations, with 190 possible baselines. As discussed above, the Effelsberg-Westerbork baseline was ignored and the calculations were thus carried out for 189 baselines only. The adopted systematic error values for the simulations with this array were the same as those adopted for the individual VLBA and EVN (Tables 1, 2 and 6) and calculations were performed for full track observations as previously. The results of these simulations (Tables 9 and 10) indicate that the astrometric errors for the global VLBI array are consistent with those found for the VLBA and the EVN. As expected, these errors are generally slightly better than the ones derived for each individual array.
Our simulations show that the astrometric accuracy of the VLBI
phase-referencing technique (defined as
![]() )
is
)
is
![]() as for mid declinations and is
as for mid declinations and is
![]() as at low and high
declinations for point sources with a relative separation of
as at low and high
declinations for point sources with a relative separation of
![]() .
The major systematic error components are the wet tropospheric
delay and the calibrator astrometric position, the latter only at
high declination. Station coordinate, Earth orientation parameter and
dry tropospheric zenith delay errors contribute generally to less than
.
The major systematic error components are the wet tropospheric
delay and the calibrator astrometric position, the latter only at
high declination. Station coordinate, Earth orientation parameter and
dry tropospheric zenith delay errors contribute generally to less than
![]() as in the error budget.
as in the error budget.
Table 12:
VLBA without Saint Croix rms astrometric errors (in ![]() as) for a relative source separation
as) for a relative source separation
![]() .
The individual astrometric error contribution from wet troposphere
uncertainties is given separately along with the total astrometric errors when all
model parameters are perturbed together.
.
The individual astrometric error contribution from wet troposphere
uncertainties is given separately along with the total astrometric errors when all
model parameters are perturbed together.
We speculated that if the VLBA station at Saint Croix in the Virgin Islands that suffers from dampness were withdrawn from the array, it should improve the astrometric accuracy of the VLBA. We thus repeated our VLBA simulations without that station. The results of this test are given in Tables 11 and 12. In contrast to our intuition, the astrometric accuracy is actually degraded when the target-calibrator direction is oriented along declination. In fact, the addition of Saint Croix strengthens the geometry of the array and improves the astrometric accuracy despite severe weather conditions. In order to further explore this question, we ran simulations without Pie Town in the middle of the array and without Mauna Kea at the far West of the array. Withdrawing Pie Town does not change the astrometric accuracy but the absence of Mauna Kea degrades the accuracy in a similar way to Saint Croix.
An important question is whether the astrometric accuracy scales linearly
as a function of the source separation. To study this matter, we
repeated all the previous simulations but with source
separations of
![]() and
and
![]() .
Then, we performed a linear fit
to the astrometric errors for the three values of the calibrator-target
separation (
.
Then, we performed a linear fit
to the astrometric errors for the three values of the calibrator-target
separation (
![]() ,
,
![]() and
and
![]() ), considering separately
each systematic error component of the tables above.
Figure 2 shows an example of such results for the
VLBA in the case of a target at
), considering separately
each systematic error component of the tables above.
Figure 2 shows an example of such results for the
VLBA in the case of a target at ![]() declination. Overall, our
plots show that the astrometric accuracy generally scales fairly linearly
as a function of the source separation.
declination. Overall, our
plots show that the astrometric accuracy generally scales fairly linearly
as a function of the source separation.
![\begin{figure}
\par\includegraphics[height=8cm,width=7cm,clip]{3021pltA.ps}\hspace*{6mm}
\includegraphics[height=8cm,width=7cm,clip]{3021pltD.ps}
\end{figure}](/articles/aa/full/2006/24/aa3021-05/Timg93.gif) |
Figure 2:
Astrometric accuracy as a function of the relative source
separation for a target-calibrator pair observed with the VLBA at a
declination of
|
| Open with DEXTER | |
To obtain a quantitative measure of the likehood of the
linearity, we determined the regression coefficients for each of the 107 linear fits. Such coefficients should be close to 1 for a linear
behavior while they should decrease as the behavior becomes less
linear. This analysis reveals that 80% of the coefficients are larger
than 0.95, indicating that the astrometric errors behave
linearly. Among all errors, calibrator position systematics are those
that were found to behave the least linearly. An empirical formula for
the astrometric accuracy
![]() has been further
estimated by averaging the parameters of all the fits:
has been further
estimated by averaging the parameters of all the fits:
As a verification of this empirical formula, we computed the
astrometric accuracy for eight target-calibrator pairs observed
with the global VLBI array as part of a project to monitor
absolute lobe motions in compact symmetric objects
(Charlot et al. 2005). For the source pair
J2212+0152/J2217+0220 with a separation of
![]() along the right ascension direction, we obtained simulated
accuracies
along the right ascension direction, we obtained simulated
accuracies
![]() as and
as and
![]() as, versus
as, versus
![]() as and
as and
![]() as when derived from Eq. (2) and Table 9. In the worst case (target-calibrator
J0754+5324/J0753+5352 with a separation of
as when derived from Eq. (2) and Table 9. In the worst case (target-calibrator
J0754+5324/J0753+5352 with a separation of
![]() along declination), simulated accuracies were
along declination), simulated accuracies were
![]() as and
as and
![]() as while
Eq. (2) and Table 10 give
as while
Eq. (2) and Table 10 give
![]() as and
as and
![]() as. Thus, overall we found
a discrepancy of a factor of 2 at most between our simple formula
(Eq. (2)) and real simulation of the case considered.
as. Thus, overall we found
a discrepancy of a factor of 2 at most between our simple formula
(Eq. (2)) and real simulation of the case considered.
We have performed extensive simulations of VLBI data with the VLBA, EVN and global VLBI array to study the dependence of the astrometric accuracy on systematic errors in the phase model of phase-referenced VLBI observations. Systematic errors considered in this study are calibrator position uncertainties, station coordinate uncertainties, Earth orientation parameters uncertainties and dry and wet troposphere errors. We have adopted state of the art VLBI values for these errors.
Our simulations show that the astrometric accuracy of a full track
phase-referenced VLBI experiment is ![]() as at mid declination and is
as at mid declination and is
![]() as at low (
as at low (
![]() )
and high (
)
and high (
![]() )
declinations for point sources angularly separated by
)
declinations for point sources angularly separated by
![]() .
Not
surprinsingly, the major systematic error originates from wet
tropospheric zenith delay uncertainties except at high declination where calibrator
position uncertainties dominate. We show that the astrometric
accuracy
.
Not
surprinsingly, the major systematic error originates from wet
tropospheric zenith delay uncertainties except at high declination where calibrator
position uncertainties dominate. We show that the astrometric
accuracy
![]() depends linearly on the source
separation and we established the simple formula
depends linearly on the source
separation and we established the simple formula
![]() where
where
![]() is
the astrometric error provided by our tables for the various arrays
and configurations and
is
the astrometric error provided by our tables for the various arrays
and configurations and
![]() is the source separation in degrees. Our
study has been carried out for point sources but variable source structure
is likely to degrade the accuracy derived from this formula.
is the source separation in degrees. Our
study has been carried out for point sources but variable source structure
is likely to degrade the accuracy derived from this formula.
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{3021figA.ps}
\end{figure}](/articles/aa/full/2006/24/aa3021-05/Timg111.gif) |
Figure A.1:
Astrometric errors
|
The analytical formulae in the Appendix A of Shapiro et al. (1979) provide
the astrometric errors caused by the inaccuracy of the calibrator
coordinates in the case of a single VLBI baseline. Adopting our
notation, these formulae become:
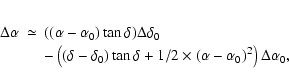
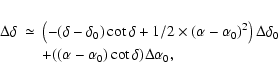
Adopting the same parameters as in our simulations (
![]() mas,
mas,
![]() mas,
mas,
![]() or
or
![]() ,
,
![]() or
or
![]() ), we obtain the astrometric errors
plotted as a function of declination in Fig. A.1 (dotted lines).
The results of our simulations for declinations of
), we obtain the astrometric errors
plotted as a function of declination in Fig. A.1 (dotted lines).
The results of our simulations for declinations of
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() and
and
![]() in the case of the VLBA
(first lines of Tables 3 and 4) are also superimposed on these plots.
in the case of the VLBA
(first lines of Tables 3 and 4) are also superimposed on these plots.
The right ascension errors obtained from the
simulations match perfectly those derived analytically, while the
declination errors show a strong discrepancy near declination
![]() (although they agree at high declinations). This discrepancy
originates from a singularity in the
(although they agree at high declinations). This discrepancy
originates from a singularity in the
![]() formula at
formula at
![]() (term in
(term in
![]() ), inherent to the approximation
used to establish the formula (baseline declination of
), inherent to the approximation
used to establish the formula (baseline declination of
![]() ). For
a more complex and realistic network, such a singularity does not
exist, as also demonstrated by the results of our simulations.
). For
a more complex and realistic network, such a singularity does not
exist, as also demonstrated by the results of our simulations.