A&A 445, 93-113 (2006)
DOI: 10.1051/0004-6361:20053200
M. Dessauges-Zavadsky1 - J. X. Prochaska2 - S. D'Odorico3 - F. Calura4 - F. Matteucci4,5
1 - Observatoire de Genève, 51 Ch. des Maillettes, 1290 Sauverny,
Switzerland
2 -
UCO/Lick Observatory, University of California at Santa Cruz, Santa
Cruz, CA 95064, USA
3 -
European Southern Observatory, Karl-Schwarzschildstr. 2, 85748
Garching bei München, Germany
4 -
Dipartimento di Astronomia-Universitá di Trieste, via G. B.
Tiepolo 11, 34131 Trieste, Italy
5 -
INAF, Osservatorio Astronomico di Trieste, via G. B. Tiepolo 11,
34131 Trieste, Italy
Received 6 April 2005 / Accepted 5 August 2005
Abstract
We present new, comprehensive sets of elemental abundances for seven damped
Ly![]() systems (DLAs) in the redshift range
systems (DLAs) in the redshift range
![]() .
These
were derived from UVES/VLT spectra combined with existing HIRES/Keck spectra. We
detected 54 metal-line transitions, and obtained the column density measurements
of 30 ions from 22 elements, - B, C, N, O, Mg, Al, Si, P, S, Cl, Ar, Ti, Cr,
Mn, Fe, Co, Ni, Cu, Zn, Ge, As, Kr. Together with the four DLAs analyzed in
Dessauges-Zavadsky et al. (2004, A&A, 416, 79), we have a sample of eleven DLA galaxies with uniquely
comprehensive and homogeneous abundance measurements. These observations allow
one to study in detail the abundance patterns of a wide range of elements and
the chemical variations in the interstellar medium of galaxies outside the
Local Group. Comparing the gas-phase abundance ratios of these high redshift
galaxies, we found that they show low rms dispersions, reaching only up 2-3
times the statistical errors for the majority of elements. This uniformity is
remarkable given that the quasar sightlines cross gaseous regions with
H I column densities spanning over one order of magnitude and
metallicities ranging from 1/55 to 1/5 solar. The uniformity is also remarkable
since DLAs are expected (and observed at low redshift) to be associated
with a wide range of galaxy types. This implies the respective star formation
histories seem to have conspired to yield one set of relative abundances.
We examined the gas-phase abundance patterns of interstellar medium "clouds''
within the DLA galaxies detected along the velocity profiles. By considering
all the clouds of all the DLAs studied together, we observe a high
dispersion in several abundance ratios, indicating that chemical variations
seem to be more confined to individual clouds within the DLA galaxies than to
integrated profiles. We found unambiguous correlations between [Si/Fe], [S/Fe]
and [S/Si] versus [Zn/Fe], and anti-correlations between [Si/Zn] and [S/Zn]
versus [Zn/Fe]. These trends are primarily the result of differential dust
depletion effects, which also explain the cloud abundance ratio dispersion. The
signature of the nucleosynthesis enrichment contribution is observed in the
[
.
These
were derived from UVES/VLT spectra combined with existing HIRES/Keck spectra. We
detected 54 metal-line transitions, and obtained the column density measurements
of 30 ions from 22 elements, - B, C, N, O, Mg, Al, Si, P, S, Cl, Ar, Ti, Cr,
Mn, Fe, Co, Ni, Cu, Zn, Ge, As, Kr. Together with the four DLAs analyzed in
Dessauges-Zavadsky et al. (2004, A&A, 416, 79), we have a sample of eleven DLA galaxies with uniquely
comprehensive and homogeneous abundance measurements. These observations allow
one to study in detail the abundance patterns of a wide range of elements and
the chemical variations in the interstellar medium of galaxies outside the
Local Group. Comparing the gas-phase abundance ratios of these high redshift
galaxies, we found that they show low rms dispersions, reaching only up 2-3
times the statistical errors for the majority of elements. This uniformity is
remarkable given that the quasar sightlines cross gaseous regions with
H I column densities spanning over one order of magnitude and
metallicities ranging from 1/55 to 1/5 solar. The uniformity is also remarkable
since DLAs are expected (and observed at low redshift) to be associated
with a wide range of galaxy types. This implies the respective star formation
histories seem to have conspired to yield one set of relative abundances.
We examined the gas-phase abundance patterns of interstellar medium "clouds''
within the DLA galaxies detected along the velocity profiles. By considering
all the clouds of all the DLAs studied together, we observe a high
dispersion in several abundance ratios, indicating that chemical variations
seem to be more confined to individual clouds within the DLA galaxies than to
integrated profiles. We found unambiguous correlations between [Si/Fe], [S/Fe]
and [S/Si] versus [Zn/Fe], and anti-correlations between [Si/Zn] and [S/Zn]
versus [Zn/Fe]. These trends are primarily the result of differential dust
depletion effects, which also explain the cloud abundance ratio dispersion. The
signature of the nucleosynthesis enrichment contribution is observed in the
[![]() /Fe,Zn] ratios at low dust depletion levels,
/Fe,Zn] ratios at low dust depletion levels,
![]() ,
and is characterized by an
,
and is characterized by an ![]() -enhancement in individual clouds.
Quite surprisingly, however, while the [Si/Fe] ratios are supersolar in clouds
with low depletion level, the [S/Zn] ratios remain almost solar, suggesting
that [S/Zn] may not be a reliable tracer of nucleosynthesis enrichment.
Analysis of the cloud-to-cloud chemical variations within seven individual DLA
systems reveals that five of them show statistically significant variations,
higher than 0.2 dex at more than 3
-enhancement in individual clouds.
Quite surprisingly, however, while the [Si/Fe] ratios are supersolar in clouds
with low depletion level, the [S/Zn] ratios remain almost solar, suggesting
that [S/Zn] may not be a reliable tracer of nucleosynthesis enrichment.
Analysis of the cloud-to-cloud chemical variations within seven individual DLA
systems reveals that five of them show statistically significant variations,
higher than 0.2 dex at more than 3![]() ,
but only two DLAs show extreme
variations. The sources of these variations are both the differential dust
depletion and/or ionization effects; however, no evidence for variations due to
different star formation histories could be highlighted. These observations
place large constraints on the mixing timescales of protogalaxies and on
scenarios of galaxy formation within the CDM hierarchical theory. Finally, we
provide an astrophysical determination of the oscillator strength of the
Ni II
,
but only two DLAs show extreme
variations. The sources of these variations are both the differential dust
depletion and/or ionization effects; however, no evidence for variations due to
different star formation histories could be highlighted. These observations
place large constraints on the mixing timescales of protogalaxies and on
scenarios of galaxy formation within the CDM hierarchical theory. Finally, we
provide an astrophysical determination of the oscillator strength of the
Ni II ![]() 1317 transition.
1317 transition.
Key words: cosmology: observations - galaxies: quasars: absorption lines - galaxies: abundances - line: profiles
One of the most exciting developments in observational cosmology over the
last decade has been the ability to extend studies of elemental abundances from
the local Universe to high redshift. This is a fundamental step toward a better
understanding of the formation and evolution of galaxies. It has been made
possible by the studies of absorption line systems detected in optical spectra
of quasars (QSOs), and specifically via the damped Ly![]() systems
(DLA; e.g. Wolfe et al. 1986). These systems with H I column densities
higher than
systems
(DLA; e.g. Wolfe et al. 1986). These systems with H I column densities
higher than
![]() cm-2 dominate the neutral gas content of the
Universe available for star formation and are, therefore, widely believed to
be progenitors of present-day galaxies
(Storrie-Lombardi & Wolfe 2000, and references therein). The DLA systems provide the best
opportunity to accurately measure the gas-phase chemical abundances of many
elements for a variety of galactic systems spanning a wide redshift interval.
These objects are by far the best laboratories for studying galaxies at high
redshifts, in their early stages of evolution.
cm-2 dominate the neutral gas content of the
Universe available for star formation and are, therefore, widely believed to
be progenitors of present-day galaxies
(Storrie-Lombardi & Wolfe 2000, and references therein). The DLA systems provide the best
opportunity to accurately measure the gas-phase chemical abundances of many
elements for a variety of galactic systems spanning a wide redshift interval.
These objects are by far the best laboratories for studying galaxies at high
redshifts, in their early stages of evolution.
In Paper I (Dessauges-Zavadsky et al. 2004), we demonstrated the efficiency and power of this approach. Indeed, we obtained comprehensive sets of elemental abundances for four DLA systems, namely the abundance measurements of 15 elements - N, O, Mg, Al, Si, P, S, Cl, Ar, Ti, Cr, Mn, Fe, Ni, and Zn - and the column density measurements of up to 21 ions. This large chemical dataset allowed us to study each galaxy individually, while previously the DLA galaxy population had been analyzed as a whole. We also provided the first constraints on their star formation history, age, and star formation rate through a detailed comparison with a grid of chemical evolution models for spiral and dwarf irregular galaxies by Calura et al. (2003). These exciting results encouraged us to further extend our sample. We obtained high quality spectra of seven additional DLAs, bringing the full sample of DLA galaxies to eleven systems.
Three main sources influence the chemical gas-phase abundance composition of
these high redshift galaxies: (i) the star formation history (SFH) through
its implications for nucleosynthesis processes; (ii) differential dust
depletion effects, since part of elements may be removed from the gas to the
solid phase (Savage & Sembach 1996); and (iii) photoionization effects, because we
are only able to measure one or a few ionization states of a given element
(Vladilo et al. 2001; Viegas 1995). The contribution of each of these three sources can
theoretically be disentangled through specific abundance ratios and is best
constrained through comprehensive sets of elemental abundances within a DLA.
There is a degeneracy between these effects that is particularly high for the
routinely detected elements (Fe, Si, Cr, Ni, Al, sometimes Zn). The specific
abundance ratios which should allow to break the degeneracy are: for (i) the
ratios involving two elements released in the interstellar medium on different
timescales, in particular the ![]() over iron-peak element ratios; for (ii)
the ratios of two elements with the same nucleosynthesis origin, but with
different dust depletion levels, like [Zn/Fe]; and for (iii) the ratios of two
elements preferentially with the same nucleosynthesis origin, but with one
element being more sensitive to ionization than the other, like [O/Si].
over iron-peak element ratios; for (ii)
the ratios of two elements with the same nucleosynthesis origin, but with
different dust depletion levels, like [Zn/Fe]; and for (iii) the ratios of two
elements preferentially with the same nucleosynthesis origin, but with one
element being more sensitive to ionization than the other, like [O/Si].
Low redshift (
![]() )
deep imaging reveals that the DLA galaxies have
a variety of morphological types (e.g. Rao et al. 2003; Nestor et al. 2002; Chen & Lanzetta 2003; Le Brun et al. 1997).
If the high redshift DLA galaxy population also samples galaxies with different
star formation histories, different stages of chemical evolution, and different
interstellar medium (ISM) conditions, we could expect to see the impact of
these differences in the chemical abundances, and highlight them through the
study of variations in the specific abundance ratios described above. A range
of at least 0.3 dex is, for example, observed in the
)
deep imaging reveals that the DLA galaxies have
a variety of morphological types (e.g. Rao et al. 2003; Nestor et al. 2002; Chen & Lanzetta 2003; Le Brun et al. 1997).
If the high redshift DLA galaxy population also samples galaxies with different
star formation histories, different stages of chemical evolution, and different
interstellar medium (ISM) conditions, we could expect to see the impact of
these differences in the chemical abundances, and highlight them through the
study of variations in the specific abundance ratios described above. A range
of at least 0.3 dex is, for example, observed in the ![]() over iron-peak
element ratios, when comparing the abundance measurements of stars in the Milky
Way with those of the Small and Large Magellanic Clouds (SMC, LMC) and dwarf
spheroidal galaxies and when comparing the abundance measurements of stars
within a given galaxy, due to different star formation histories
(Venn 1999; Tolstoy et al. 2003; Shetrone et al. 2003). Similarly there is a greater than
0.5 dex range in the gas-phase abundances of different lines of sight crossing
the Milky Way and Magellanic Clouds due to different physical conditions, e.g.
various dust-to-gas ratios, volume densities and ionization states within the
ISM (Welty et al. 2001; Savage & Sembach 1996; Welty et al. 1999).
over iron-peak
element ratios, when comparing the abundance measurements of stars in the Milky
Way with those of the Small and Large Magellanic Clouds (SMC, LMC) and dwarf
spheroidal galaxies and when comparing the abundance measurements of stars
within a given galaxy, due to different star formation histories
(Venn 1999; Tolstoy et al. 2003; Shetrone et al. 2003). Similarly there is a greater than
0.5 dex range in the gas-phase abundances of different lines of sight crossing
the Milky Way and Magellanic Clouds due to different physical conditions, e.g.
various dust-to-gas ratios, volume densities and ionization states within the
ISM (Welty et al. 2001; Savage & Sembach 1996; Welty et al. 1999).
Even though DLA galaxies have H I column densities spanning an order of magnitude and metallicities spread over two orders of magnitude, previous studies show that DLAs have similar abundance ratios suggesting that these protogalaxies have common enrichment histories (Prochaska & Wolfe 2002). In the same way, the abundance patterns of DLA "clouds'' for a given system also show uniformity suggesting that the gas of these protogalaxies has a similar enrichment history and uniform differential dust depletion (Prochaska 2003; Lopez et al. 2002; Prochaska & Wolfe 1996). If confirmed, these results have important implications for the ISM of high redshift galaxies and the enrichment of gas in the early Universe.
In this paper, we further investigate the issue of chemical variations in the
abundance ratios of both DLA galaxies and DLA gas along the velocity profiles.
We focus on our sample of eleven DLAs with comprehensive sets of elemental
abundances. This sample comprises the four DLAs studied in Paper I and the seven
new DLAs presented here (Sects. 2 and 3). We
discuss the global abundance patterns of DLAs in Sect. 4, and in
Sects. 5 and 6 we study the abundance
patterns of clouds within the DLA galaxies, which we regard as individual
entities. First, we consider all the clouds of all the DLAs from our sample
together (Sect. 5), and second we focus on the cloud-to-cloud
chemical analysis within a single DLA (Sect. 6). In
Sect. 7 we summarize our results. Finally, we present an
astrophysical determination of the oscillator strength of the
Ni II ![]() 1317 transition in Appendix A. In two
future papers, Paper III and Paper IV of this series, we will further analyze
this sample of DLAs. In Paper III, we will study their star formation history,
age, and star formation rate through a detailed comparison with chemical
evolution models, and in Paper IV we plan to analyze in detail their ionization
state through comparisons of the observed ionic ratios against photoionization
models. Two DLAs of our sample are likely to have among the highest ionization
levels of all previously studied DLA galaxies.
1317 transition in Appendix A. In two
future papers, Paper III and Paper IV of this series, we will further analyze
this sample of DLAs. In Paper III, we will study their star formation history,
age, and star formation rate through a detailed comparison with chemical
evolution models, and in Paper IV we plan to analyze in detail their ionization
state through comparisons of the observed ionic ratios against photoionization
models. Two DLAs of our sample are likely to have among the highest ionization
levels of all previously studied DLA galaxies.
Table 1: Journal of observations.
The selected quasars Q0450-13, Q0841+129, Q1157+014, Q1210+17, Q2230+02, and
Q2348-1444 with seven intervening DLAs in the redshift range
![]() are relatively bright with
V = 16.5-18.5. Their spectra have already
been reported in the literature, and four of them have been studied by
Prochaska & Wolfe (1999) and Prochaska et al. (2001) using high resolution, high quality
spectra obtained with the HIRES echelle spectrograph on the Keck I 10 m
telescope at Mauna Kea, Hawaii. More details on these DLA systems and the
existing data can be found in Sect. 3. This sample of six QSOs completes our first sample of QSOs, - Q0100+13, Q1331+17, Q2231-00,
and Q2343+12 -, with the same characteristics in redshift and magnitude as
studied in Paper I. The combination of these two sets of observations provides
an impressive sample of eleven damped Ly
are relatively bright with
V = 16.5-18.5. Their spectra have already
been reported in the literature, and four of them have been studied by
Prochaska & Wolfe (1999) and Prochaska et al. (2001) using high resolution, high quality
spectra obtained with the HIRES echelle spectrograph on the Keck I 10 m
telescope at Mauna Kea, Hawaii. More details on these DLA systems and the
existing data can be found in Sect. 3. This sample of six QSOs completes our first sample of QSOs, - Q0100+13, Q1331+17, Q2231-00,
and Q2343+12 -, with the same characteristics in redshift and magnitude as
studied in Paper I. The combination of these two sets of observations provides
an impressive sample of eleven damped Ly![]() systems with comprehensive
elemental abundances.
systems with comprehensive
elemental abundances.
We used the unique capability of the Ultraviolet-Visual Echelle Spectrograph
UVES (D'Odorico et al. 2000) on the VLT 8.2 m Kueyen ESO telescope at Cerro
Paranal, Chile, to obtain high resolution, high signal-to-noise ratio spectra
of our QSOs in the total optical spectral range, or to complete the existing
HIRES/Keck spectra in the blue
![]() Å and in the far-red
Å and in the far-red
![]() Å. The observations were performed in service mode
in period 70 from October 2002 to April 2003 (programme ID No. 70.B-0258)
under good seeing conditions (between 0.5
Å. The observations were performed in service mode
in period 70 from October 2002 to April 2003 (programme ID No. 70.B-0258)
under good seeing conditions (between 0.5
![]() and 1
and 1
![]() ). For one
object, Q1157+014, we used spectra from the ESO UVES/VLT archive (programme ID
No. 65.O-063, 67.A-0078, and 68.A-0461). For each science exposure, slit
widths of 1
). For one
object, Q1157+014, we used spectra from the ESO UVES/VLT archive (programme ID
No. 65.O-063, 67.A-0078, and 68.A-0461). For each science exposure, slit
widths of 1
![]() in the blue and of 0.9
in the blue and of 0.9
![]() in red were used with a CCD
binning of
in red were used with a CCD
binning of ![]() ,
resulting in a resolution
,
resulting in a resolution
![]() km s-1
and 6.4 km s-1 on average, respectively. Relevant details on the
observations are collected in Table 1. The total exposure times
of each QSO were split in multiple exposures of 3600 or 4500 s.
km s-1
and 6.4 km s-1 on average, respectively. Relevant details on the
observations are collected in Table 1. The total exposure times
of each QSO were split in multiple exposures of 3600 or 4500 s.
The spectra were reduced using the ESO data reduction package MIDAS and
the UVES pipeline in an interactive mode available as a MIDAS context. A
detailed description of the pipeline can be found in Ballester et al. (2000). To
optimize the results, we made a systematic check of each step of the pipeline
reduction. Once reduced, the wavelengths of the resulting one-dimensional
spectra were converted to a vacuum-heliocentric scale. For QSOs with multiple
exposures, the individual spectra were co-added using their signal-to-noise
ratio as weights. The spectra were normalized by smoothly connecting regions
free from absorption features with a spline function. In the Ly![]() forest,
the continuum was fitted by using small regions deemed to be free from
absorptions and by interpolating between these regions with a spline. An
average signal-to-noise ratio per pixel of
forest,
the continuum was fitted by using small regions deemed to be free from
absorptions and by interpolating between these regions with a spline. An
average signal-to-noise ratio per pixel of ![]() 25, 45, and 40 was achieved
in the final spectra at
25, 45, and 40 was achieved
in the final spectra at
![]() ,
7000, and 9000 Å, respectively.
,
7000, and 9000 Å, respectively.
By combining our UVES/VLT spectra with the existing HIRES/Keck spectra of Q0841+129, Q1210+17, Q2230+02, and Q2348-1444, we covered the total spectral range from 3060 to 10 000 Å for the six selected QSOs. This gave us access to several metal-line transitions of 22 elements for each of their intervening DLAs. In this section we present the derived ionic column density measurements.
The ionic column densities were obtained using the Voigt profile fitting
technique. This technique consists of fitting theoretical Voigt profiles to
the observed DLA absorption profiles. These profiles are described well as a
complex of components, each defined by a redshift z, a Doppler parameter b,
a column density N and the corresponding errors. The fits were performed
using an ![]() minimization routine FITLYMAN in MIDAS
(Fontana & Ballester 1995). We assumed that metal species with similar ionization
potentials can be fitted using identical component fitting parameters, i.e. the
same b (which means that macroturbulent motions dominate over thermal
broadening) and the same z in the same component, and allowing for variations
from metal species to metal species in N only. We distinguish three categories
of metal species with similar ionization potentials: the low-ion transitions
(i.e. the neutral and singly ionized species), the intermediate-ion transitions
(e.g. Fe III, Al III), and the high-ion transitions (e.g.
C IV, Si IV). By using relatively strong (but not saturated) lines
to fix the component fitting parameters (the b and z values for each
component), we then obtained excellent fitting results even for weak metal lines
and for metal lines in the Ly
minimization routine FITLYMAN in MIDAS
(Fontana & Ballester 1995). We assumed that metal species with similar ionization
potentials can be fitted using identical component fitting parameters, i.e. the
same b (which means that macroturbulent motions dominate over thermal
broadening) and the same z in the same component, and allowing for variations
from metal species to metal species in N only. We distinguish three categories
of metal species with similar ionization potentials: the low-ion transitions
(i.e. the neutral and singly ionized species), the intermediate-ion transitions
(e.g. Fe III, Al III), and the high-ion transitions (e.g.
C IV, Si IV). By using relatively strong (but not saturated) lines
to fix the component fitting parameters (the b and z values for each
component), we then obtained excellent fitting results even for weak metal lines
and for metal lines in the Ly![]() forest, where the probability of blending
is high, by allowing only the column density to vary. We had a sufficient
number of relatively strong metal lines to accurately constrain the fitting
parameters in the seven DLAs studied that exhibited multicomponent velocity
structures.
forest, where the probability of blending
is high, by allowing only the column density to vary. We had a sufficient
number of relatively strong metal lines to accurately constrain the fitting
parameters in the seven DLAs studied that exhibited multicomponent velocity
structures.
In Tables 2-8 we present the results of the
component per component ionic column density measurements for the fitting model
solutions of the low- and intermediate-ion transitions for the seven DLA
systems analyzed. The reported errors are the 1![]() errors on the fits
computed by FITLYMAN. These errors do not take the uncertainties on the
continuum level determination into account, unless it is mentioned in
Sects. 3.1-3.7. For the saturated components, the column
densities are listed as lower limits. The values reported as upper limits are
either cases with significant line blendings by H I lines in the
Ly
errors on the fits
computed by FITLYMAN. These errors do not take the uncertainties on the
continuum level determination into account, unless it is mentioned in
Sects. 3.1-3.7. For the saturated components, the column
densities are listed as lower limits. The values reported as upper limits are
either cases with significant line blendings by H I lines in the
Ly![]() forest or telluric lines or cases of non-detection corresponding to 4
forest or telluric lines or cases of non-detection corresponding to 4![]() limits. By adopting a conservative 4
limits. By adopting a conservative 4![]() upper limit based
on the statistical error, we account - in part - the continuum error. In
Figs. 2-14 (even numbers), we show the best
fitting solutions of all the low- and intermediate-ion transitions detected
in the seven DLAs studied. In these velocity plots, v=0 corresponds to an
arbitrary component, and all the identified components are marked by small
vertical bars. The thin solid line represents the best fit. The telluric lines
have been identified thanks to the spectrum of a hot, fast rotating star taken
on the same night as the science exposures.
upper limit based
on the statistical error, we account - in part - the continuum error. In
Figs. 2-14 (even numbers), we show the best
fitting solutions of all the low- and intermediate-ion transitions detected
in the seven DLAs studied. In these velocity plots, v=0 corresponds to an
arbitrary component, and all the identified components are marked by small
vertical bars. The thin solid line represents the best fit. The telluric lines
have been identified thanks to the spectrum of a hot, fast rotating star taken
on the same night as the science exposures.
The neutral hydrogen column densities were measured from the fit of the
Ly![]() damping line profile. The b-value was fixed at 20 km s-1,
and the redshift z was left as a free parameter or fixed at the redshift of
the strongest component of the metal-line profile depending on the DLA system
(see the comments in the following sub-sections). When other lines of higher
members of the Lyman series were accessible in our spectra, they were used in
parallel to the Ly
damping line profile. The b-value was fixed at 20 km s-1,
and the redshift z was left as a free parameter or fixed at the redshift of
the strongest component of the metal-line profile depending on the DLA system
(see the comments in the following sub-sections). When other lines of higher
members of the Lyman series were accessible in our spectra, they were used in
parallel to the Ly![]() line to derive the H I column density.
In Figs. 1-13 (odd numbers), we show the best
H I fitting solutions in the seven DLAs studied. The small vertical bar
corresponds to the redshift used in the best-fitting solution, and the thin
solid line represents the best fit.
line to derive the H I column density.
In Figs. 1-13 (odd numbers), we show the best
H I fitting solutions in the seven DLAs studied. The small vertical bar
corresponds to the redshift used in the best-fitting solution, and the thin
solid line represents the best fit.
Throughout the analysis we have adopted the list of atomic data, laboratory
wavelengths and oscillator strengths, compiled by J. X. Prochaska and
collaborators (version 0.5) and presented on the web site "the HIRES Damped
Ly![]() Abundance Database''
Abundance Database''![]() .
The most recent measurements of
.
The most recent measurements of
![]() and f-values of the
metal-line transitions that impact the abundances of DLAs and their references
are reported there. In Appendix A we present an updated value of
the Ni II
and f-values of the
metal-line transitions that impact the abundances of DLAs and their references
are reported there. In Appendix A we present an updated value of
the Ni II ![]() 1317 oscillator strength derived from different
Ni II transitions detected in the DLAs studied. We adopt the solar
meteoritic abundances from Grevesse & Sauval (1998).
1317 oscillator strength derived from different
Ni II transitions detected in the DLAs studied. We adopt the solar
meteoritic abundances from Grevesse & Sauval (1998).
This quasar was discovered by C. Hazard and was first investigated by
Jaunsen et al. (1995). The presence of the DLA system at
![]() on
its line of sight was communicated to us by J. X. Prochaska (private
communication). This is the first detailed analysis of its chemical composition.
The high quality UVES/VLT spectra cover the total spectral range from 3060
to 10 000 Å. These data permit analysis of some 39 metal-line transitions
and help to obtain accurate column density measurements of Fe II,
Si II, Al II, S II, N I, P II, Mg II,
C II*, Al III, Fe III, and N II. In addition, we
were able to put very reliable upper limits to the column densities of
Ni II, Cr II, and Ar I and to provide a lower limit to the
column density of O I.
on
its line of sight was communicated to us by J. X. Prochaska (private
communication). This is the first detailed analysis of its chemical composition.
The high quality UVES/VLT spectra cover the total spectral range from 3060
to 10 000 Å. These data permit analysis of some 39 metal-line transitions
and help to obtain accurate column density measurements of Fe II,
Si II, Al II, S II, N I, P II, Mg II,
C II*, Al III, Fe III, and N II. In addition, we
were able to put very reliable upper limits to the column densities of
Ni II, Cr II, and Ar I and to provide a lower limit to the
column density of O I.
The low-ion absorption line profiles of this DLA are characterized by 13
components spread over 230 km s-1 in velocity space (see
Fig. 2). Their redshifts, b-values, and column densities are
presented in Table 2. Only the components 4-9 are detected in
weak metal-line transitions, they contain approximately 80% of the total
column density obtained by summing the contribution of the 13 components. The
accessible Ni II lines at
![]() ,
1751 Å,
Cr II lines at
,
1751 Å,
Cr II lines at
![]() ,
2062, 2066 Å, and
Ar I lines at
,
2062, 2066 Å, and
Ar I lines at
![]() ,
1066 Å are all so weak
that we consider their derived column densities as upper limits. In the
context of upper limits, the column density of P+ is a borderline case.
However, the P II
,
1066 Å are all so weak
that we consider their derived column densities as upper limits. In the
context of upper limits, the column density of P+ is a borderline case.
However, the P II ![]() 1152 line has a slightly higher optical
depth than the Ni II and Cr II lines, we thus assumed it is a
detection. In contrast, the O I line at
1152 line has a slightly higher optical
depth than the Ni II and Cr II lines, we thus assumed it is a
detection. In contrast, the O I line at
![]() Å
is saturated in the components 4-7, so we only got a lower limit to
its total column density. The Mg+ column density was obtained from the
unsaturated Mg II
Å
is saturated in the components 4-7, so we only got a lower limit to
its total column density. The Mg+ column density was obtained from the
unsaturated Mg II ![]() 1239, 1240 lines. Because these
Mg II transitions are located in the red wing of the DLA Ly
1239, 1240 lines. Because these
Mg II transitions are located in the red wing of the DLA Ly![]() damping profile, it is difficult to obtain an accurate column density
measurement of Mg+. To estimate the column density, we first normalized the
spectra within the damped Ly
damping profile, it is difficult to obtain an accurate column density
measurement of Mg+. To estimate the column density, we first normalized the
spectra within the damped Ly![]() profile near the Mg II lines
according to the fit of the Ly
profile near the Mg II lines
according to the fit of the Ly![]() damping wing profile. We applied the
same procedure to the N I triplet at
damping wing profile. We applied the
same procedure to the N I triplet at
![]() Å, which is located in the blue wing of the DLA Ly
Å, which is located in the blue wing of the DLA Ly![]() damping profile.
The 1
damping profile.
The 1![]() errors on the measured N(Mg+) and N(N0) column
densities were estimated by varying the continuum level by 5%. No
Zn II line was detected in this DLA system. We provide a 4
errors on the measured N(Mg+) and N(N0) column
densities were estimated by varying the continuum level by 5%. No
Zn II line was detected in this DLA system. We provide a 4![]() upper limit to the Zn+ column density of
upper limit to the Zn+ column density of ![]() (Zn II) < 11.60.
(Zn II) < 11.60.
The intermediate-ion absorption line profiles show a different velocity
structure than the low-ion line profiles (see Fig. 2). Their
fitting solution is presented in the second part of Table 2.
However, in velocity space the positions of the 6 components characterizing
the intermediate-ion line profiles correspond very closely to the positions of
components 1, 3, 4, 6, and 8 of low-ion lines. When considering the column
density ratios of different ionization species of the same element, we find the
following very interesting results:
![]() (Al++)/N(Al+) =
(Al++)/N(Al+) =
![]() ,
,
![]() (Fe++)/N(Fe+)
(Fe++)/N(Fe+)
![]() larger
than -1, and
larger
than -1, and ![]() (N+)/N(N0) =
(N+)/N(N0) =
![]() larger than -0.2.
Those ratios give a qualitative "first-look'' analysis of the ionization
state in a DLA. According to the photoionization diagnostics described by
Prochaska et al. (2002a), we have clear evidence in this DLA of a very high
ionization level. This will be further discussed in Paper IV of this series.
In Sect. 6 we present additional indications toward the
presence of strong ionization in this system.
larger than -0.2.
Those ratios give a qualitative "first-look'' analysis of the ionization
state in a DLA. According to the photoionization diagnostics described by
Prochaska et al. (2002a), we have clear evidence in this DLA of a very high
ionization level. This will be further discussed in Paper IV of this series.
In Sect. 6 we present additional indications toward the
presence of strong ionization in this system.
Finally, Fig. 1 shows the fitting solution of two Lyman lines
of this DLA, Ly![]() and Ly
and Ly![]() .
The fits were obtained by fixing the
b-value at 20 km s-1 and the redshift at z=2.06666, i.e. at the
redshift of one of the stronger metal-line components (the component 6 at
v = -14 km s-1). The derived H I column density is
.
The fits were obtained by fixing the
b-value at 20 km s-1 and the redshift at z=2.06666, i.e. at the
redshift of one of the stronger metal-line components (the component 6 at
v = -14 km s-1). The derived H I column density is
![]() (H I)
(H I)
![]() .
This is a relatively high value,
especially in light of the evidence mentioned above for the high ionization
level in this DLA (Vladilo et al. 2001).
.
This is a relatively high value,
especially in light of the evidence mentioned above for the high ionization
level in this DLA (Vladilo et al. 2001).
The two DLA systems at
![]() and at
and at
![]() toward the quasar Q0841+129 were identified by C. Hazard and were first studied
at low resolution by Pettini et al. (1997). More recently, high resolution spectra
obtained with HIRES/Keck and UVES/VLT were analyzed by Prochaska & Wolfe (1999),
Prochaska et al. (2001), Centurión et al. (2003), Ledoux et al. (2003), and
Vladilo et al. (2003).
toward the quasar Q0841+129 were identified by C. Hazard and were first studied
at low resolution by Pettini et al. (1997). More recently, high resolution spectra
obtained with HIRES/Keck and UVES/VLT were analyzed by Prochaska & Wolfe (1999),
Prochaska et al. (2001), Centurión et al. (2003), Ledoux et al. (2003), and
Vladilo et al. (2003).
In the case of the first DLA at
![]() ,
we confirm the
Prochaska & Wolfe (1999) and Prochaska et al. (2001) column density measurements of
Fe II, Si II, Ni II, Cr II, and Zn II.
However, our column density measurements of Fe II, Zn II,
S II, and Ar I differ by almost 0.1 dex from those of
Centurión et al. (2003) and Vladilo et al. (2003). This discrepancy is likely to be the
result of the lower signal-to-noise ratio in their UVES/VLT spectra and an
underestimation of their uncertainties. In the cases of Fe+, Zn+, and
Ar0, we used at least two different metal-line transitions to derive the column densities; e.g. for N(Fe+) 9 transitions are considered (see
Fig. 4). We, nevertheless, confirm the
Centurión et al. (2003) N(N0) measurement, obtained in our analysis using
both the N I triplet at
,
we confirm the
Prochaska & Wolfe (1999) and Prochaska et al. (2001) column density measurements of
Fe II, Si II, Ni II, Cr II, and Zn II.
However, our column density measurements of Fe II, Zn II,
S II, and Ar I differ by almost 0.1 dex from those of
Centurión et al. (2003) and Vladilo et al. (2003). This discrepancy is likely to be the
result of the lower signal-to-noise ratio in their UVES/VLT spectra and an
underestimation of their uncertainties. In the cases of Fe+, Zn+, and
Ar0, we used at least two different metal-line transitions to derive the column densities; e.g. for N(Fe+) 9 transitions are considered (see
Fig. 4). We, nevertheless, confirm the
Centurión et al. (2003) N(N0) measurement, obtained in our analysis using
both the N I triplet at
![]() and
and ![]() 1200 Å, except the N I
1200 Å, except the N I ![]() 1134.165 line which is blended with
H I lines in the Ly
1134.165 line which is blended with
H I lines in the Ly![]() forest.
forest.
From a total of 46 metal-line transitions detected and analyzed (see Fig. 4), we obtained the column density measurements of Mg II, Mn II, P II, C II*, Al III, and Fe III, in addition to the ions discussed above. We also derived lower limits to the column densities of O I and Al II and upper limits to N(C I) and N(S III).
The low-ion absorption line profiles of this DLA are characterized by a simple
velocity structure composed of 6 components spread over 80 km s-1. Their
properties are described in Table 3. Only the components 3 and 4 are detected in the weaker metal-line transitions. They contain,
however, ![]() 95% of the total column density of the fully integrated
profile. Due to the high H I column density of this DLA system and the
proximity of the second DLA at
95% of the total column density of the fully integrated
profile. Due to the high H I column density of this DLA system and the
proximity of the second DLA at
![]() on the same QSO line of
sight, the N I triplet at
on the same QSO line of
sight, the N I triplet at
![]() Å is located
in the blue wing of the DLA Ly
Å is located
in the blue wing of the DLA Ly![]() damping line profile, the
Mg II
damping line profile, the
Mg II ![]() 1239, 1240 lines in the red wing of the DLA Ly
1239, 1240 lines in the red wing of the DLA Ly![]() line, and the S II
line, and the S II ![]() 1259 line, the only unblended S II
line available, in the red wing of the Ly
1259 line, the only unblended S II
line available, in the red wing of the Ly![]() damping line profile of the
second DLA. Consequently, we renormalized the damped Ly
damping line profile of the
second DLA. Consequently, we renormalized the damped Ly![]() profiles of both
DLAs according to their best values, in order to derive accurate column
densities of N0, Mg+, and S+. The 1
profiles of both
DLAs according to their best values, in order to derive accurate column
densities of N0, Mg+, and S+. The 1![]() errors on the measured
column densities are estimated by varying the continuum level by 5%. The
S II
errors on the measured
column densities are estimated by varying the continuum level by 5%. The
S II ![]() 1259 line shows a slight asymmetry in its profile
compared to other low-ion metal lines, which is not perfectly modeled in our
solution. The Mg I
1259 line shows a slight asymmetry in its profile
compared to other low-ion metal lines, which is not perfectly modeled in our
solution. The Mg I ![]() 2026 line in Fig. 4
is plotted to illustrate that there is no contamination of
Zn II
2026 line in Fig. 4
is plotted to illustrate that there is no contamination of
Zn II ![]() 2026 by Mg0.
2026 by Mg0.
The intermediate-ion line profiles of this DLA are composed of only two
components with very similar characteristics to the main components 3 and 4 of
the low-ion lines (see the second part of Table 3). The
derived S++ column density measurement is a borderline case between a
detection and an upper limit due to possible blends with H I lines in the
Ly![]() forest. To be conservative, we assumed it is an upper limit.
Following the Prochaska et al. (2002a) photoionization diagnostics, we used the
column density ratios of different ionization species of the same element
measured in this DLA to infer the ionization state. Specifically the ratios
-
forest. To be conservative, we assumed it is an upper limit.
Following the Prochaska et al. (2002a) photoionization diagnostics, we used the
column density ratios of different ionization species of the same element
measured in this DLA to infer the ionization state. Specifically the ratios
- ![]() (Al++)/N(Al
+) < -1.22,
(Al++)/N(Al
+) < -1.22, ![]() (Fe++)/N(Fe+)
(Fe++)/N(Fe+)
![]() ,
and
,
and ![]() (S++)/N(S+) < -0.53 - indicate
that this system has a low ionization level, with an ionization fraction,
defined as the ratio of H+ over (H0 + H+), lower than 10%.
(S++)/N(S+) < -0.53 - indicate
that this system has a low ionization level, with an ionization fraction,
defined as the ratio of H+ over (H0 + H+), lower than 10%.
The determination of the H I column densities from the Ly![]() damping
lines of the two DLAs toward Q0841+129 was particularly difficult in this case
because of the proximity of the two systems (separated by 9040 km s-1
only). The detections of the Ly
damping
lines of the two DLAs toward Q0841+129 was particularly difficult in this case
because of the proximity of the two systems (separated by 9040 km s-1
only). The detections of the Ly![]() line in the DLA at
line in the DLA at
![]() and the Ly
and the Ly![]() and Ly
and Ly![]() lines in the DLA at
lines in the DLA at
![]() in
our UVES/VLT spectra provide an indirect check on the fits. In
Figs. 3 and 5, we show the derived results
for the two DLAs. In both systems, we fitted all the lines of the Lyman series
simultaneously, and we fixed the b-value at 20 km s-1 and the redshift
at
z = 2.37452 and
z = 2.47621, respectively, i.e. at the redshift of the
strongest metal-line component (the component 4 and 2, respectively). The
derived H I column densities,
in
our UVES/VLT spectra provide an indirect check on the fits. In
Figs. 3 and 5, we show the derived results
for the two DLAs. In both systems, we fitted all the lines of the Lyman series
simultaneously, and we fixed the b-value at 20 km s-1 and the redshift
at
z = 2.37452 and
z = 2.47621, respectively, i.e. at the redshift of the
strongest metal-line component (the component 4 and 2, respectively). The
derived H I column densities, ![]() (H I)
(H I)
![]() for
the first DLA and
for
the first DLA and ![]() (H I)
(H I)
![]() for the second DLA,
are in a very good agreement with the values from Centurión et al. (2003) and
Vladilo et al. (2003).
for the second DLA,
are in a very good agreement with the values from Centurión et al. (2003) and
Vladilo et al. (2003).
As mentioned in Sect. 3.2, this DLA system toward Q0841+129 has
already been studied by several authors at high resolution. Using our UVES/VLT
spectra combined with the existing HIRES/Keck spectra, we obtained a high
signal-to-noise ratio and a total optical wavelength coverage, which allowed us
to analyze 45 different metal-line transitions (see
Fig. 6). We obtained the column density measurements of
Fe II, Si II, N I, S II, O I, Ar I,
Mg II, P II, Mn II, Ni II, Cr II,
Zn II, and Al III. We also derived lower limits to the column
densities of C II and Al II from saturated lines, and upper limits
to the column densities of C II*, Fe III, N II, and
S III. Discrepancies between 0.05 and 0.1 dex are observed between
our column density measurements and those obtained by Prochaska & Wolfe (1999),
Prochaska et al. (2001), Centurión et al. (2003), and Vladilo et al. (2003). In the majority
of cases, we used a larger number of metal-line transitions to measure the
column density of a given ion, which appreciably increases the accuracy of the
measurement, especially in those cases where the transitions lie outside the
Ly![]() forest. In addition, in the case of the N I, S II, and
Ar I lines, we benefited from a signal-to-noise ratio that is twice
as high as the spectra used by Centurión et al. (2003) and Vladilo et al. (2003).
forest. In addition, in the case of the N I, S II, and
Ar I lines, we benefited from a signal-to-noise ratio that is twice
as high as the spectra used by Centurión et al. (2003) and Vladilo et al. (2003).
The low-ion absorption line profiles of this DLA are characterized by only 3 components spread over 20 km s-1 (see Table 4). The
component 1 is only observed in the stronger metal-line transitions and it
contributes negligibly to the total column density. In weak metal-line
transitions, the component 3 is only marginally detected, like for instance in
Ar I, P II, Mn II, and Ni II (see
Fig. 6). Thus, for several ions we adopted large errors
on their component 3 column density measurements. The column density
measurement of O0 is a borderline case between a detection and a limit. It
was derived from the saturated O I ![]() 1039 line, which
gives a constraint on the lower limit to N(O0) and the
O I
1039 line, which
gives a constraint on the lower limit to N(O0) and the
O I ![]() 950 line far in the blue, exposed to several possible
line blendings, which provides a constraint on the upper limit to N(O0).
By fitting these two lines simultaneously, we assumed that we get a reliable
column density measurement of O0. Granted the large uncertainty, we adopted
a conservative error estimate. The determination of N(P+) was also
challenging. However, the value derived from the P II
950 line far in the blue, exposed to several possible
line blendings, which provides a constraint on the upper limit to N(O0).
By fitting these two lines simultaneously, we assumed that we get a reliable
column density measurement of O0. Granted the large uncertainty, we adopted
a conservative error estimate. The determination of N(P+) was also
challenging. However, the value derived from the P II ![]() 963
line, far in the blue (perhaps blended with H I lines in the Ly
963
line, far in the blue (perhaps blended with H I lines in the Ly![]() forest), agrees perfectly with the weak P II
forest), agrees perfectly with the weak P II ![]() 1152
line. Therefore, we assumed the measured N(P+) value is a good detection.
Finally, the measurements of the column densities of Mg+ and Zn+ are
borderline cases between detections and upper limits. Indeed, the observed
Zn II
1152
line. Therefore, we assumed the measured N(P+) value is a good detection.
Finally, the measurements of the column densities of Mg+ and Zn+ are
borderline cases between detections and upper limits. Indeed, the observed
Zn II ![]() 2026, 2062 and Mg II
2026, 2062 and Mg II ![]() 1239, 1240 lines are very weak, detected at 3
1239, 1240 lines are very weak, detected at 3![]() only. Therefore, we report
conservatively large errors for their column density measurements.
only. Therefore, we report
conservatively large errors for their column density measurements.
In the intermediate-ion line profiles of this DLA, we detected a single
component which has the same characteristics as the strongest component of
low-ion lines, component 2 (see Table 4). We obtained
the column density measurements of four intermediate-ions, Al++, Fe++,
N+, and S++. To be conservative, we considered three of them,
- N(Fe++), N(N+), and N(S++) -, as upper limits due to
possible blends with H I lines in the Ly![]() forest (see
Fig. 6). These measurements lead to the following column
density ratios for different ionization species of the same element:
forest (see
Fig. 6). These measurements lead to the following column
density ratios for different ionization species of the same element:
![]() (Al++)/N(Al+) < -0.78,
(Al++)/N(Al+) < -0.78, ![]() (Fe++)/N(Fe+)
<-0.95,
(Fe++)/N(Fe+)
<-0.95, ![]() (N+)/N(N0) <-0.40, and
(N+)/N(N0) <-0.40, and
![]() (S++)/N(S+) < -0.76. According to the photoionization
diagnostics of Prochaska et al. (2002a), these ratios show the gas is predominantly
neutral.
(S++)/N(S+) < -0.76. According to the photoionization
diagnostics of Prochaska et al. (2002a), these ratios show the gas is predominantly
neutral.
This DLA system was first identified by Wolfe & Briggs (1981) at 21 cm. They obtained
an estimation of its H0 column density of ![]() (H I)
(H I)
![]() .
This value is an important reference to check our measurement of
N(H I) derived from UVES/VLT high resolution spectra. In
Fig. 7 we show the Ly
.
This value is an important reference to check our measurement of
N(H I) derived from UVES/VLT high resolution spectra. In
Fig. 7 we show the Ly![]() line of the DLA system. Only the
blue wing is plotted, because of the very uncertain normalization of the red
Ly
line of the DLA system. Only the
blue wing is plotted, because of the very uncertain normalization of the red
Ly![]() damping wing, given its proximity to the QSO Ly
damping wing, given its proximity to the QSO Ly![]() emission peak
(
emission peak
(
![]() Å). By fixing the b-value at 20 km s-1 and the
redshift at
z = 1.94366, i.e. at the redshift of the strongest metal-line
component (the component 4), we obtained a good fit of the blue Ly
Å). By fixing the b-value at 20 km s-1 and the
redshift at
z = 1.94366, i.e. at the redshift of the strongest metal-line
component (the component 4), we obtained a good fit of the blue Ly![]() damping wing profile. The measured H I column density,
damping wing profile. The measured H I column density,
![]() (H I)
(H I)
![]() ,
is consistent with the value obtained
by Wolfe & Briggs (1981). In addition, our measurement is in a very good agreement
with the H0 column density,
,
is consistent with the value obtained
by Wolfe & Briggs (1981). In addition, our measurement is in a very good agreement
with the H0 column density, ![]() (H I)
(H I)
![]() ,
also
measured from high resolution spectra by Ledoux et al. (2003).
,
also
measured from high resolution spectra by Ledoux et al. (2003).
This DLA, with its high H I column density and high metallicity
(>1021 cm-2, [Zn/H]
![]() ), belongs to the category of
"metal-strong'' DLA systems defined by Prochaska et al. (2003). These systems
show strong metal absorption lines and, as a consequence, allow the ionic
column density measurements of a very large number of ions and elements. Indeed,
in this DLA system, for instance, 54 metal-line transitions were detected
(see Fig. 8). We obtained accurate column density measurements
of Fe II, Si II, Mg II, P II, C II*,
Mn II, Ni II, Cr II, Zn II, Ti II,
Co II, Ge II, Mg I, and Al III. We also derived
lower limits to the column densities of Al II and N I and upper
limits to the column densities of C I, B II, Cl I,
Cu II, Kr I, and As II.
), belongs to the category of
"metal-strong'' DLA systems defined by Prochaska et al. (2003). These systems
show strong metal absorption lines and, as a consequence, allow the ionic
column density measurements of a very large number of ions and elements. Indeed,
in this DLA system, for instance, 54 metal-line transitions were detected
(see Fig. 8). We obtained accurate column density measurements
of Fe II, Si II, Mg II, P II, C II*,
Mn II, Ni II, Cr II, Zn II, Ti II,
Co II, Ge II, Mg I, and Al III. We also derived
lower limits to the column densities of Al II and N I and upper
limits to the column densities of C I, B II, Cl I,
Cu II, Kr I, and As II.
The low-ion absorption line profiles of this DLA are characterized by 7
components spread over 145 km s-1. Their redshifts, b-values, and column
densities are presented in Table 5. The components 1 and 7 are
only observed in the stronger metal lines and make a negligible contribution to
the total ionic column densities. The problem of contamination of the
Zn II ![]() 2026 line by the Mg I
2026 line by the Mg I ![]() 2026 line was
first raised by Prochaska et al. (2001). To control the impact of this blend on the
Zn+ column density measurement, we needed to know the level of the
contribution of Mg0 in the Zn II line. For this purpose, we used the
Mg I
2026 line was
first raised by Prochaska et al. (2001). To control the impact of this blend on the
Zn+ column density measurement, we needed to know the level of the
contribution of Mg0 in the Zn II line. For this purpose, we used the
Mg I ![]() 2852 line, which gives an accurate estimate of the
contamination at 2026 Å (see Fig. 8). One drawback
of the high H I column density of this DLA is that the blue Ly
2852 line, which gives an accurate estimate of the
contamination at 2026 Å (see Fig. 8). One drawback
of the high H I column density of this DLA is that the blue Ly![]() damping line wing overlaps the N I triplet at
damping line wing overlaps the N I triplet at
![]() Å. Therefore, we locally renormalized the spectrum with the fit of the
Ly
Å. Therefore, we locally renormalized the spectrum with the fit of the
Ly![]() damping wing profile to derive a column density of N0. An
additional difficulty related to the N(N I) measurement is that
the profile is probably saturated. Indeed, the components 5 and 6 look almost
saturated even in the weaker N I transitions, e.g. in the lines at
damping wing profile to derive a column density of N0. An
additional difficulty related to the N(N I) measurement is that
the profile is probably saturated. Indeed, the components 5 and 6 look almost
saturated even in the weaker N I transitions, e.g. in the lines at
![]() ,
1134.980, and 1200.710 Å, and the
weakest N I line at
,
1134.980, and 1200.710 Å, and the
weakest N I line at
![]() Å is strongly
blended with H I lines in the Ly
Å is strongly
blended with H I lines in the Ly![]() forest to be relevant. We are
thus inclined to assume that the derived N0 column density is a lower limit.
In contrast, the P II column density measurement is a borderline case
between a detection and an upper limit. Indeed, the P II
forest to be relevant. We are
thus inclined to assume that the derived N0 column density is a lower limit.
In contrast, the P II column density measurement is a borderline case
between a detection and an upper limit. Indeed, the P II ![]() 1152
line shows signs of possible blends with H I lines in the Ly
1152
line shows signs of possible blends with H I lines in the Ly![]() forest mainly toward the blue edge. However, its fit agrees perfectly with the
weaker P II
forest mainly toward the blue edge. However, its fit agrees perfectly with the
weaker P II ![]() 1532 line (see Fig. 8). We thus
assume that the measured N(P+) is a detection.
1532 line (see Fig. 8). We thus
assume that the measured N(P+) is a detection.
The high H I column density and the relatively high metallicity of this
DLA allowed us to obtain column density measurements and reliable upper
limits of some very weak metal-line transitions. We obtained a very accurate
column density measurement of Ti II from the detection and analysis of
several Ti II lines at
![]() ,
1910.938, 3067,
and 3073 Å. More exceptionally, at 3
,
1910.938, 3067,
and 3073 Å. More exceptionally, at 3![]() we detected the
Co II
we detected the
Co II ![]() 2012 and Ge II
2012 and Ge II ![]() 1237 lines (see
Fig. 8). Only two detections of Co+ in DLAs have been
reported by Ellison et al. (2001) and Rao et al. (2005) and one previous
measurement of Ge+ by Prochaska et al. (2003). We are concerned that the
observed Co and Ge profiles do not show significant optical depth at v=0,
but we suppose that this is within the statistical error adopted on their
column density measurement. We also obtained very reliable 4
1237 lines (see
Fig. 8). Only two detections of Co+ in DLAs have been
reported by Ellison et al. (2001) and Rao et al. (2005) and one previous
measurement of Ge+ by Prochaska et al. (2003). We are concerned that the
observed Co and Ge profiles do not show significant optical depth at v=0,
but we suppose that this is within the statistical error adopted on their
column density measurement. We also obtained very reliable 4![]() upper
limits to the column densities of B+, Cl0, Cu+, Kr0, and As+
from the undetected but clean, i.e. free from blending and with a high
signal-to-noise ratio, B II
upper
limits to the column densities of B+, Cl0, Cu+, Kr0, and As+
from the undetected but clean, i.e. free from blending and with a high
signal-to-noise ratio, B II ![]() 1362,
Cl I
1362,
Cl I ![]() 1347, Cu II
1347, Cu II ![]() 1358,
Kr I
1358,
Kr I ![]() 1164, and As II
1164, and As II ![]() 1355 lines.
Previously, only Prochaska et al. (2003) have put meaningful upper limits to the
column densities of these ions in another metal-strong DLA system.
1355 lines.
Previously, only Prochaska et al. (2003) have put meaningful upper limits to the
column densities of these ions in another metal-strong DLA system.
The intermediate-ion line profiles have the same shape and characteristics as
the low-ion line profiles in this DLA (see Fig. 8 and
Table 5). We obtained the column density measurement of
Al III and an upper limit to N(Fe III) from the
Fe III ![]() 1122 line located in the Ly
1122 line located in the Ly![]() forest and
probably blended with H I lines, by using the same fitting parameters as
those defined for the low-ion lines. The measured very low column density ratio,
forest and
probably blended with H I lines, by using the same fitting parameters as
those defined for the low-ion lines. The measured very low column density ratio,
![]() (Al++)/N(Al
+) < -1.82, clearly shows that the ionization is
negligible in this DLA, strongly self-shielded by the high neutral hydrogen
column density gas (Prochaska et al. 2002a).
(Al++)/N(Al
+) < -1.82, clearly shows that the ionization is
negligible in this DLA, strongly self-shielded by the high neutral hydrogen
column density gas (Prochaska et al. 2002a).
This DLA system toward Q1210+17 was discovered by Wolfe et al. (1995) and is a member of the Large Bright QSO Survey. It has already been studied at high resolution by Prochaska et al. (2001). Using our UVES/VLT spectra combined with their HIRES/Keck spectra, we confirm their column density measurements of Fe II, Si II, Ni II, Cr II, and Zn II at 0.05 dex. In addition, we obtained the column density measurements of S II, N I, Mn II, Ti II, and Al III, lower limits to the column density of Al II and Mg II, and an upper limit to the column density of P II from a total of 45 metal-line transitions analyzed (see Fig. 10).
The low-ion absorption line profiles of this DLA are characterized by a simple
velocity structure, composed of 7 components spread over 130 km s-1. Their
properties are described in Table 6. Only the components 3, 4,
and 5 were detected in the weak metal-line transitions. They contain nearly
all of the column density of the profile (![]() 95%). The derived column
density of N0 is a borderline case between a detection and an upper limit
due to possible blends with H I lines in the Ly
95%). The derived column
density of N0 is a borderline case between a detection and an upper limit
due to possible blends with H I lines in the Ly![]() forest. All the
available N I lines seem to be blended, although luckily not over the
whole profile. In this way, we succeeded in constraining the column densities
of components 3, 4, and 5 by fitting them to the various N I lines. We
believe that we obtained a reliable N(N0) but report a conservatively large
error estimate. The measurement of the column density of Mg+ is also tricky.
The saturated Mg II
forest. All the
available N I lines seem to be blended, although luckily not over the
whole profile. In this way, we succeeded in constraining the column densities
of components 3, 4, and 5 by fitting them to the various N I lines. We
believe that we obtained a reliable N(N0) but report a conservatively large
error estimate. The measurement of the column density of Mg+ is also tricky.
The saturated Mg II ![]() 2796, 2803 lines provide a lower limit
to N(Mg+), while the Mg II
2796, 2803 lines provide a lower limit
to N(Mg+), while the Mg II ![]() 1239, 1240 lines in the
Ly
1239, 1240 lines in the
Ly![]() forest give an upper limit to the column density of the component 4.
The upper limit to the column density of P+ was obtained from the
P II
forest give an upper limit to the column density of the component 4.
The upper limit to the column density of P+ was obtained from the
P II ![]() 1152, 1532 lines. The Mg I
1152, 1532 lines. The Mg I ![]() 2026
line in Fig. 10 illustrates that the
Zn II
2026
line in Fig. 10 illustrates that the
Zn II ![]() 2026 line is not contaminated by Mg0.
2026 line is not contaminated by Mg0.
The intermediate-ion lines of this DLA show exactly the same profiles as the
low-ion lines (see Fig. 10 and Table 6). We
obtained the column density measurement of Al++ only. This DLA has a very
low column density ratio ![]() (Al++)/N(Al+) < -1.96, which
clearly indicates that the ionization is very low in this system
(Prochaska et al. 2002a).
(Al++)/N(Al+) < -1.96, which
clearly indicates that the ionization is very low in this system
(Prochaska et al. 2002a).
Figure 9 shows the fitting solution of the Ly![]() line of this
DLA. The fit was obtained by fixing the b-value at 20 km s-1 and the
redshift at z=1.89177, i.e. at the redshift of the strongest metal-line
component (the component 4). The derived H I column density is
line of this
DLA. The fit was obtained by fixing the b-value at 20 km s-1 and the
redshift at z=1.89177, i.e. at the redshift of the strongest metal-line
component (the component 4). The derived H I column density is
![]() (H I) =
(H I) =
![]() ,
which agrees well with
the value obtained by Wolfe et al. (1995) from low resolution spectra. This DLA
system exhibits a high metallicity of
,
which agrees well with
the value obtained by Wolfe et al. (1995) from low resolution spectra. This DLA
system exhibits a high metallicity of
![]() ,
and hence
almost belongs to the category of metal-strong DLAs (Prochaska et al. 2003).
Therefore, we were able to derive a very accurate Ti+ column density
measurement from the detection of several Ti II lines at
,
and hence
almost belongs to the category of metal-strong DLAs (Prochaska et al. 2003).
Therefore, we were able to derive a very accurate Ti+ column density
measurement from the detection of several Ti II lines at
![]() ,
3073, 3242, and 3384 Å. In addition, we obtained
reliable 4
,
3073, 3242, and 3384 Å. In addition, we obtained
reliable 4![]() upper limits to the column densities of Kr0 and As+ from the
undetected Kr I
upper limits to the column densities of Kr0 and As+ from the
undetected Kr I ![]() 1164 and As II
1164 and As II ![]() 1263
lines, respectively. The Ge II
1263
lines, respectively. The Ge II ![]() 1237 line is unfortunately
blended, and the B II
1237 line is unfortunately
blended, and the B II ![]() 1362, Cu II
1362, Cu II ![]() 1358,
O I
1358,
O I ![]() 1355, and Co II lines are not covered in our high
signal-to-noise ratio UVES/VLT spectra, with which we could probably have
provided reliable upper limits or detections of these ions in this DLA (see
Sect. 3.4).
1355, and Co II lines are not covered in our high
signal-to-noise ratio UVES/VLT spectra, with which we could probably have
provided reliable upper limits or detections of these ions in this DLA (see
Sect. 3.4).
This DLA system is an object from the Large Bright QSO Survey (Wolfe et al. 1995). It has been studied at low resolution by Pettini et al. (1994), and more recently at high resolution by Prochaska & Wolfe (1999) and Prochaska et al. (2001). Prochaska & Wolfe (1999) have analyzed this DLA extensively thanks to the detection of 28 metal-line transitions in their HIRES/Keck spectra. We confirm their column density measurements of Fe II, Si II, Ni II, Cr II, and Al III at 0.05 dex. However, our column density measurements of Zn II and Ti II differ by more than 0.05 dex, as described below. From a total of 46 metal-line transitions detected and analyzed (see Fig. 12), we obtained, in addition, the column density measurements of S II, N I, P II, Mn II, C II*, and Mg I, and an upper limit to the column density of Fe III.
The low-ion absorption line profiles of this DLA are characterized by a very
complex velocity structure extended over 400 km s-1 in velocity space and
composed of 21 components presented in Table 7. Three important
clumps at -41, +17, and +74 km s-1 composed of mainly 4 components, the
components 9, 12, 13, and 14, dominate the profile. They contain about 75%
of the total column density obtained by summing the contribution of the 21
components. This complex velocity structure of low-ion lines made the
determination of the N0 column density very difficult. Indeed, due to the
large velocity spread of the profiles, the three lines of the N I
triplets at
![]() and at
and at ![]() 1200 Å are
blended together, but luckily not too heavily contaminated by H I lines
in the Ly
1200 Å are
blended together, but luckily not too heavily contaminated by H I lines
in the Ly![]() forest (see Fig. 12). By careful work on
the 6 N I lines available in our UVES/VLT spectra and by using the
fitting parameters constrained with unblended and uncontaminated low-ion lines,
we finally derived an accurate N0 column density.
The Zn+ column density measurement also needed some attention, due to a
possible blend of the Zn II
forest (see Fig. 12). By careful work on
the 6 N I lines available in our UVES/VLT spectra and by using the
fitting parameters constrained with unblended and uncontaminated low-ion lines,
we finally derived an accurate N0 column density.
The Zn+ column density measurement also needed some attention, due to a
possible blend of the Zn II ![]() 2026 line with the
Mg I
2026 line with the
Mg I ![]() 2026 line. The Mg I
2026 line. The Mg I ![]() 2852 line
allowed us to very accurately determine the contamination of the Zn II
column density by Mg0 by obtaining a fit of the Mg I
2852 line
allowed us to very accurately determine the contamination of the Zn II
column density by Mg0 by obtaining a fit of the Mg I ![]() 2026
line. This contamination is lower than 0.1 dex, but it explains the discrepancy
between Prochaska & Wolfe (1999) Zn+ column density measurement,
2026
line. This contamination is lower than 0.1 dex, but it explains the discrepancy
between Prochaska & Wolfe (1999) Zn+ column density measurement,
![]() (Zn II) =
(Zn II) =
![]() ,
and our weaker value,
,
and our weaker value,
![]() (Zn II) =
(Zn II) =
![]() .
.
In the saturated O I ![]() 1302 and Al II
1302 and Al II ![]() 1670
lines, we measured the column densities of the unsaturated components only (see
Table 7). The column density of the component 9 of
C II* is referred to as an upper limit because the blue edge of the
C II*
1670
lines, we measured the column densities of the unsaturated components only (see
Table 7). The column density of the component 9 of
C II* is referred to as an upper limit because the blue edge of the
C II* ![]() 1335 line is blended with the
C II
1335 line is blended with the
C II ![]() 1334 line. The Mg II
1334 line. The Mg II ![]() 1239, 1240
lines were undetected in this DLA, so we provide only a 4
1239, 1240
lines were undetected in this DLA, so we provide only a 4![]() upper
limit to the column density of Mg+. Despite the low signal-to-noise ratio
per pixel of 8 in the wavelength regions covering the S II and
P II lines, we obtained accurate S+ and P+ column densities.
Finally, we derived a very accurate column density measurement of Ti+,
thanks to the access to several Ti II lines at
upper
limit to the column density of Mg+. Despite the low signal-to-noise ratio
per pixel of 8 in the wavelength regions covering the S II and
P II lines, we obtained accurate S+ and P+ column densities.
Finally, we derived a very accurate column density measurement of Ti+,
thanks to the access to several Ti II lines at
![]() ,
1910.938, 3073, 3242, and 3384 Å. Our N(Ti+) differs from the
one of Prochaska & Wolfe (1999) obtained from the two Ti II lines at
,
1910.938, 3073, 3242, and 3384 Å. Our N(Ti+) differs from the
one of Prochaska & Wolfe (1999) obtained from the two Ti II lines at
![]() Å, which have a 2-3 times weaker oscillator
strength than the Ti II
Å, which have a 2-3 times weaker oscillator
strength than the Ti II ![]() 3242, 3384 lines used in our
measurement.
3242, 3384 lines used in our
measurement.
Only 11 components were detected in the intermediate-ion line profiles of this
DLA. They show very similar characteristics as the components 5 to 15 of the
low-ion lines (see the second part of Table 7 and
Fig. 12). We obtained a column density measurement of Al++and an upper limit to N(Fe++) from the Fe III ![]() 1122
line probably blended with H I lines in the Ly
1122
line probably blended with H I lines in the Ly![]() forest. The
measured low column density ratios,
forest. The
measured low column density ratios, ![]() (Al++)/N(Al
+) < -0.43
and
(Al++)/N(Al
+) < -0.43
and ![]() (Fe++)/N(Fe
+) < -0.61, clearly show that this DLA
system has a low ionization level (Prochaska et al. 2002a).
(Fe++)/N(Fe
+) < -0.61, clearly show that this DLA
system has a low ionization level (Prochaska et al. 2002a).
While fitting the Ly![]() damping line profile at z=1.86375 (redshift of
one of the stronger metal-line components, the component 12), we found it
necessary to include the contribution of a second absorber shifted by about 550 km s-1 bluewards the DLA system (see Fig. 11). The redshift of
this second absorber, z=1.85851, was accurately determined from several
associated metal lines. Pettini et al. (1994) already discovered the presence of
these two closeby absorption line systems in their low resolution spectra by
observing that the metal lines consist of two main components separated by
damping line profile at z=1.86375 (redshift of
one of the stronger metal-line components, the component 12), we found it
necessary to include the contribution of a second absorber shifted by about 550 km s-1 bluewards the DLA system (see Fig. 11). The redshift of
this second absorber, z=1.85851, was accurately determined from several
associated metal lines. Pettini et al. (1994) already discovered the presence of
these two closeby absorption line systems in their low resolution spectra by
observing that the metal lines consist of two main components separated by
![]() 550 km s-1. The derived H I column densities are
550 km s-1. The derived H I column densities are
![]() (H I) =
(H I) =
![]() for the DLA and
for the DLA and ![]() (H I) =
(H I) =
![]() for the second absorber. They agree well with the values
obtained by Pettini et al. (1994).
for the second absorber. They agree well with the values
obtained by Pettini et al. (1994).
This DLA system was first discussed by Pettini et al. (1994) and first studied at
high resolution by Pettini et al. (1995). Subsequently it was carefully
analyzed by Prochaska & Wolfe (1999) and Prochaska et al. (2002b) using HIRES/Keck
spectra. We confirm their column density measurements of Fe II,
Si II, S II, Al II, and C II* at 0.05 dex, and
their lower limit to the column density of O I derived from the saturated
O I ![]() 1302 line. From a total of 36 metal-line transitions
detected and analyzed (see Fig. 14), we obtained the column
density measurements of N I, Mn II, Cr II, Al III,
and Fe III, in addition, and upper limits to the column densities of
Mg II, Ni II, Zn II, and S III.
1302 line. From a total of 36 metal-line transitions
detected and analyzed (see Fig. 14), we obtained the column
density measurements of N I, Mn II, Cr II, Al III,
and Fe III, in addition, and upper limits to the column densities of
Mg II, Ni II, Zn II, and S III.
The low-ion absorption line profiles of this DLA are characterized by a very
simple velocity structure composed of 4 components spread over 40 km s-1.
Their properties are described in Table 8. Component 4 was
only detected in the stronger metal-line transitions and its contribution to
the total column density is negligible. Many metal lines observed in this DLA
are very weak, and their column density measurements are borderline cases
between detections and upper limits. This is the case for the Mg II,
Mn II, Ni II, Cr II, and Zn II lines. Only the
Mn II and Cr II lines were detected at 3![]() ;
hence, by
adopting large errors we obtained reliable Mn+ and Cr+ column densities.
For the other lines detected at less than 3
;
hence, by
adopting large errors we obtained reliable Mn+ and Cr+ column densities.
For the other lines detected at less than 3![]() ,
we provided valuable
upper limits. While the very weak Mg II
,
we provided valuable
upper limits. While the very weak Mg II ![]() 1239, 1240 lines
gave an upper limit to N(Mg+), the saturated
Mg II
1239, 1240 lines
gave an upper limit to N(Mg+), the saturated
Mg II ![]() 2796, 2803 lines led to a lower limit to N(Mg+)
(see Table 8). We consider the derived C II* column
density in agreement with the value obtained by Prochaska & Wolfe (1999) as an upper
limit due to possible blends of the C II*
2796, 2803 lines led to a lower limit to N(Mg+)
(see Table 8). We consider the derived C II* column
density in agreement with the value obtained by Prochaska & Wolfe (1999) as an upper
limit due to possible blends of the C II* ![]() 1335 line with
H I lines in the Ly
1335 line with
H I lines in the Ly![]() forest. Similarly we prefer to assume that
the measured Al II column density is an upper limit due to a possible
blend of the Al II
forest. Similarly we prefer to assume that
the measured Al II column density is an upper limit due to a possible
blend of the Al II ![]() 1670 line with a metal line (see
Fig. 14). Thanks to our access to several N I lines, we
could derive a value for the first time and not only an upper limit to the
N0 column density (Pettini et al. 1995; Prochaska et al. 2002b). However, before fitting
the N I lines, we first had to locally renormalize the spectrum around
the N I triplet at
1670 line with a metal line (see
Fig. 14). Thanks to our access to several N I lines, we
could derive a value for the first time and not only an upper limit to the
N0 column density (Pettini et al. 1995; Prochaska et al. 2002b). However, before fitting
the N I lines, we first had to locally renormalize the spectrum around
the N I triplet at
![]() Å with the fit of
the blue DLA Ly
Å with the fit of
the blue DLA Ly![]() damping wing profile.
damping wing profile.
The intermediate-ion lines of this DLA show exactly the same profiles as the
low-ion lines (see Fig. 14 and Table 8). We
obtained the column density measurements of Al++ and Fe++ from the
Fe III ![]() 1122 line located in the Ly
1122 line located in the Ly![]() forest. The
Fe III line might be blended with H I lines, so we adopted a
large error on N(Fe++). We also derived an upper limit to the column
density of S III. These measurements lead to the following column
density ratios of different ionization species of the same element:
forest. The
Fe III line might be blended with H I lines, so we adopted a
large error on N(Fe++). We also derived an upper limit to the column
density of S III. These measurements lead to the following column
density ratios of different ionization species of the same element:
![]() (Al++)/N(Al+) > -0.66,
(Al++)/N(Al+) > -0.66, ![]() (Fe++)/N(Fe+)
(Fe++)/N(Fe+)
![]() ,
and
,
and ![]() (S++)/N(S+) < +0.04. According to the
photoionization diagnostics of Prochaska et al. (2002a) , these ratios show that
the DLA system is likely to be partially ionized. The ionization fraction is,
however, lower than 50% and the expected ionization corrections on the
measured ionic column densities are on the order of only 0.1 dex. The most
important corrections to the observed gas-phase abundances are that the
intrinsic [Si/Fe] ratio is slightly lower and the intrinsic [N/Si,S] ratios are
slightly higher.
(S++)/N(S+) < +0.04. According to the
photoionization diagnostics of Prochaska et al. (2002a) , these ratios show that
the DLA system is likely to be partially ionized. The ionization fraction is,
however, lower than 50% and the expected ionization corrections on the
measured ionic column densities are on the order of only 0.1 dex. The most
important corrections to the observed gas-phase abundances are that the
intrinsic [Si/Fe] ratio is slightly lower and the intrinsic [N/Si,S] ratios are
slightly higher.
Figure 13 shows the fitting solution of the Ly![]() line of this
DLA system. The fit was obtained by fixing the b-value at 20 km s-1 and
the redshift at z=2.27939, i.e. at the redshift of the strongest metal-line
component (component 3). The derived H I column density is
line of this
DLA system. The fit was obtained by fixing the b-value at 20 km s-1 and
the redshift at z=2.27939, i.e. at the redshift of the strongest metal-line
component (component 3). The derived H I column density is ![]() (H I) =
(H I) =
![]() ,
which agrees well with the value obtained by
Pettini et al. (1994) from low resolution spectra.
,
which agrees well with the value obtained by
Pettini et al. (1994) from low resolution spectra.
In the next three sections we will use the results obtained for the seven DLAs studied here (see Sect. 3) in combination with the results derived in Paper I for four DLAs. These eleven DLAs constitute the first sample of high redshift objects for which we have the following at our disposal: accurate column density measurements of individual interstellar medium "clouds'' within the DLAs detected along the velocity profiles; the column density measurements of up to 30 ions; and the abundance measurements of up to 22 elements.
![\begin{figure}
\par\includegraphics[width=13cm,clip]{3200fig22.ps}
\end{figure}](/articles/aa/full/2006/01/aa3200-05/Timg73.gif) |
Figure 15: Nucleosynthetic abundance patterns [X/Si] ( upper panel) and [X/Fe] ( lower panel) for our sample of 11 DLAs. We consider the entire set of detected elements X covering a large range of atomic numbers from 5 to 36. The plotted abundance ratios are the raw abundance ratio measurements, i.e. the directly observed gas-phase abundance ratios, free from any correction (dust or ionization). Our sample of data is composed of the 7 DLAs studied in this paper (open circles) and of 4 DLAs analyzed in Paper I (filled squares). In Table 9 we present some statistical results relative to the observed abundance pattern trends. |
| Open with DEXTER | |
The absolute abundances, [X/H], are obtained by summing the contributions of all the components detected in the element X profile and reported in Tables 2-8. In what follows we will discuss the abundance ratios, [X/Y]. These are computed by considering only the column densities of components detected in both the element X and Y profiles. This is equivalent to comparing X and Y over the exact same velocity intervals. In this way we prevent an overestimation of abundances derived from strong metal-line profiles relative to the abundances derived from weaker metal-line profiles in which only the stronger components are usually detected. In the case of very weak metal lines, like the Ti II lines for instance, one can indeed underestimate the [X/Fe] ratios by up to 0.3-0.4 dex by considering the total Fe abundance generally derived by summing a much larger number of components than for the Ti abundance. This effect is particularly important in DLAs with complex metal-line profiles extended over a large velocity range, in which a large difference is observed between the number of components detected in strong and weak metal lines. In our sample this is mainly the case of the DLAs toward Q0450-13 and toward Q2230+02. The same approach was already used in Paper I, where the DLAs toward Q2231-00 and toward Q2343+12 were subject to such uncertainties.
Figure 15 shows the nucleosynthetic abundance patterns as
a function of the atomic number of the seven DLAs studied in this paper
(open circles) and the four DLAs studied in Paper I (filled squares). We present
both the [X/Si] and [X/Fe] abundance ratios relative to the solar values for
the entire set of 22 detected elements X covering a range of atomic numbers
from 5 to 36. This contrasts with the majority of DLAs for which only a handful
of elements is usually detected (e.g. Prochaska et al. 2001; Prochaska & Wolfe 1999; Lu et al. 1996).
We consider here the raw abundance ratios free from any correction (dust or
ionization). In this way we can try to identify whether the SFH, dust depletion,
or ionization has a perceptible impact on some abundance ratios, and we can
study the dispersion in the abundance patterns of the DLA galaxy population. In
Table 9 we present some statistical results on the observed
abundance pattern trends. We computed the logarithmic weighted mean of the
[X/Si] and [X/Fe] abundance ratios using their 1![]() errors as weights,
the logarithmic rms dispersion in [X/Si] and [X/Fe] ratios, and the reduced
errors as weights,
the logarithmic rms dispersion in [X/Si] and [X/Fe] ratios, and the reduced ![]() of [X/Si] and [X/Fe] relative to their weighted mean. The numbers
in parentheses are given for information only. They correspond to the abundance
ratios [X/Si] and [X/Fe] computed by considering all of the gas in the
Si II and Fe II profiles, in comparison to the adopted method
for the computation of the [X/Si] and [X/Fe] ratios (see the beginning of this
section). To be conservative we do not take the limits in these calculations
into account. We do note, however, that the limits would only lead to an
increased dispersion in abundance ratios in which the detections already show a
dispersion, e.g. P and Ti (see Fig. 15).
of [X/Si] and [X/Fe] relative to their weighted mean. The numbers
in parentheses are given for information only. They correspond to the abundance
ratios [X/Si] and [X/Fe] computed by considering all of the gas in the
Si II and Fe II profiles, in comparison to the adopted method
for the computation of the [X/Si] and [X/Fe] ratios (see the beginning of this
section). To be conservative we do not take the limits in these calculations
into account. We do note, however, that the limits would only lead to an
increased dispersion in abundance ratios in which the detections already show a
dispersion, e.g. P and Ti (see Fig. 15).
We underline that, although the abundance ratio measurements presented here are
the raw ones (i.e. the directly observed gas-phase abundances), they show a
remarkable uniformity![]() . Indeed, in the 11 DLA systems studied with
redshifts between 1.7 and 2.5, H I column densities covering one order
of magnitude from
. Indeed, in the 11 DLA systems studied with
redshifts between 1.7 and 2.5, H I column densities covering one order
of magnitude from
![]() to
to
![]() cm-2, and
metallicities from 1/55 to 1/5 solar, the abundance patterns show relatively
low rms dispersions, reaching only up to 2-3 times higher values than the
statistical errors
cm-2, and
metallicities from 1/55 to 1/5 solar, the abundance patterns show relatively
low rms dispersions, reaching only up to 2-3 times higher values than the
statistical errors![]() for the majority of elements. This
suggests that the effects of nucleosynthesis enrichment, dust depletion, and
ionization are negligible and that the abundance ratios of the integrated
profiles for the DLA galaxy population are very uniform, as pointed out by
Molaro (2005). In turn, this implies the respective star formation histories
have conspired to yield one set of relative abundances.
The time interval sampled by the DLA galaxies studied is of 1.8 Gyr for the
adopted H0 = 65 km s-1 Mpc-1,
for the majority of elements. This
suggests that the effects of nucleosynthesis enrichment, dust depletion, and
ionization are negligible and that the abundance ratios of the integrated
profiles for the DLA galaxy population are very uniform, as pointed out by
Molaro (2005). In turn, this implies the respective star formation histories
have conspired to yield one set of relative abundances.
The time interval sampled by the DLA galaxies studied is of 1.8 Gyr for the
adopted H0 = 65 km s-1 Mpc-1,
![]() ,
and
,
and
![]() cosmology.
cosmology.
Table 9: Abundance patterns of the integrated profiles for our sample of 11 DLAs.
We now discuss element per element the results derived for the [X/Si] and [X/Fe] ratios, along with their implications:
N: The [N/Si] and [N/Fe] ratios both show a
large dispersion, larger than 0.2 dex, with [N/Si] values ranging from -0.8
to -1.5. We expect that the large dispersion is due to different star
formation histories (SFH) and ages of DLA galaxies, as discussed by a number of
authors (see Chiappini et al. 2003; Pettini et al. 2002; Prochaska et al. 2002b; Centurión et al. 2003). We do
not wish to review the details here.
While variations in the star formation histories are most likely the principal
source of [N/Si] and [N/Fe] dispersions, ionization effects may also be
important. Indeed, N0 has a larger cross-section to photons with ![]() Ryd than H0 (Sofia & Jenkins 1998). Both in the DLA toward Q0450-13 and the DLA
toward Q2343+12 with strong evidence for high ionization levels, we observe
that a significant fraction of N is in the form of N+ and not N0 only. As
a consequence N0/(Si+, Fe+) will underestimate N/(Si, Fe)
(Prochaska et al. 2002b).
Ryd than H0 (Sofia & Jenkins 1998). Both in the DLA toward Q0450-13 and the DLA
toward Q2343+12 with strong evidence for high ionization levels, we observe
that a significant fraction of N is in the form of N+ and not N0 only. As
a consequence N0/(Si+, Fe+) will underestimate N/(Si, Fe)
(Prochaska et al. 2002b).
Mg: Aside from the measurement of
Srianand et al. (2000), the six Mg abundance measurements from our sample are the
only Mg abundances derived in DLAs to date. The large dispersions observed in
the [Mg/Si] and [Mg/Fe] ratios of +0.45 and +0.38 dex, respectively, are due to
the upper open circle which corresponds to the DLA toward Q0450-13. This DLA
shows several clues for a high ionization fraction (see Sect. 3.1).
Hence, the measured abundance of Mg+ is easily overestimated by several
tenths of dex (see Fig. 5 in Dessauges-Zavadsky et al. 2002), which leads to the
high [Mg/Si] and [Mg/Fe] ratios observed in this DLA. Mg is an ![]() -element
and it should at least roughly trace Si as observed in Galactic metal-poor
stars (François et al. 2004), although Si is probably produced in non-negligible
amounts by type Ia supernovae (SNe) in addition to type II SNe. This is
confirmed by our data, when excluding the DLA toward Q0450-13.
-element
and it should at least roughly trace Si as observed in Galactic metal-poor
stars (François et al. 2004), although Si is probably produced in non-negligible
amounts by type Ia supernovae (SNe) in addition to type II SNe. This is
confirmed by our data, when excluding the DLA toward Q0450-13.
Si: The low [Si/Fe] dispersion (0.11 dex,
![]() )
indicates that the [Si/Fe] ratio remains nearly
constant irrespective of the DLA galaxy and its dust depletion level. The mean
[Si/Fe] value of +0.43 dex then suggests on average a high
)
indicates that the [Si/Fe] ratio remains nearly
constant irrespective of the DLA galaxy and its dust depletion level. The mean
[Si/Fe] value of +0.43 dex then suggests on average a high ![]() -element
enhancement relative to iron-peak elements in all DLA systems, which is an
enrichment by massive stars. Indeed, the
-element
enhancement relative to iron-peak elements in all DLA systems, which is an
enrichment by massive stars. Indeed, the ![]() -elements are produced in less
than
-elements are produced in less
than
![]() yrs by type II SNe resulting from massive stars, while the
iron-peak elements are mainly produced by type Ia SNe on longer timescales
between
yrs by type II SNe resulting from massive stars, while the
iron-peak elements are mainly produced by type Ia SNe on longer timescales
between
![]() and 109 yrs (Matteucci & Recchi 2001).
and 109 yrs (Matteucci & Recchi 2001).
P: P cannot be measured in Galactic halo
stars; thus the recent entry of P in the set of elements observed in DLAs
offers a unique astronomical site where it can be measured at metallicities
significantly lower than solar. The [P/Si] and [P/Fe] ratios show a large
dispersion. The [P/Si] ratio is particularly interesting for observing the
odd-even effect as it corresponds to an underabundance of odd-Z elements
relative to even-Z elements of the same nucleosynthetic origin. The mean [P/Si]
value of -0.13 shows evidence of a mild odd-even effect, lower than the
expectations on the basis of yields by Woosley & Weaver (1995) and Limongi et al. (2000).
However, some DLAs show a strong odd-even effect, as the DLA at
![]() toward Q0841+129 with [P/Si]
toward Q0841+129 with [P/Si]
![]() .
This leads to a high
[P/Si] dispersion due to various strengths of the odd-even effect from galaxy
to galaxy. We emphasize that P is a non-refractory element and the variations
are not very likely to be related to differential depletion.
.
This leads to a high
[P/Si] dispersion due to various strengths of the odd-even effect from galaxy
to galaxy. We emphasize that P is a non-refractory element and the variations
are not very likely to be related to differential depletion.
S: The [S/Si] ratio shows a relatively low
dispersion and a mean solar value. This implies that S traces Si very closely
as in Galactic halo stars. Hence, the refractory ![]() -element Si appears to
be almost insensitive to dust depletion effects at the level they are observed
in the DLAs studied, since it traces the volatile
-element Si appears to
be almost insensitive to dust depletion effects at the level they are observed
in the DLAs studied, since it traces the volatile ![]() -element S whatever
the dust depletion. The [S/Fe] ratio shows a large rms dispersion of
0.19 dex, larger than the one for the [Si/Fe] ratio. As a consequence, it might
appear that the [S/Fe] ratio is more subject to variations due to dust
depletion or nucleosynthesis enrichment than the [Si/Fe] ratio, but only in the
order of the weak variations allowed by the [S/Si] ratios. The low reduced
-element S whatever
the dust depletion. The [S/Fe] ratio shows a large rms dispersion of
0.19 dex, larger than the one for the [Si/Fe] ratio. As a consequence, it might
appear that the [S/Fe] ratio is more subject to variations due to dust
depletion or nucleosynthesis enrichment than the [Si/Fe] ratio, but only in the
order of the weak variations allowed by the [S/Si] ratios. The low reduced
![]() of the [S/Fe] ratio values of 4.2 confirms that the [S/Fe] intrinsic
variations are in fact low and that [S/Fe] remains almost constant as [Si/Fe],
whatever the DLA galaxy and its dust depletion level might be. The mean [S/Fe]
value of +0.33 dex suggests, on average, an
of the [S/Fe] ratio values of 4.2 confirms that the [S/Fe] intrinsic
variations are in fact low and that [S/Fe] remains almost constant as [Si/Fe],
whatever the DLA galaxy and its dust depletion level might be. The mean [S/Fe]
value of +0.33 dex suggests, on average, an ![]() -element enhancement in all
DLA systems as the [Si/Fe] ratio.
-element enhancement in all
DLA systems as the [Si/Fe] ratio.
Cl: We obtained a measurement and an upper limit to the column density of Cl I. They both yield upper limits to the Cl abundance, since the dominant state of Cl in DLAs is Cl+ and not Cl0. Indeed, most of Cl I is probably ionized, given that the ionization potential of Cl0 is lower than 1 Ryd. Unfortunately, no general abundance pattern trend can be discussed for this element (see Paper I for a description of its importance).
Ar: Ar is a typical product of type II SNe.
It is presumed to track other ![]() -elements, although there is little
empirical evidence. No Ar abundance measurement exists in Galactic stars, and
thus Ar measurements in DLAs are of high priority in the search to better
understand the behavior of this element. The measured [Ar/Si] ratios have a low
dispersion of 0.14 dex with a very low reduced
-elements, although there is little
empirical evidence. No Ar abundance measurement exists in Galactic stars, and
thus Ar measurements in DLAs are of high priority in the search to better
understand the behavior of this element. The measured [Ar/Si] ratios have a low
dispersion of 0.14 dex with a very low reduced ![]() .
Interestingly, all the
obtained Ar measurements show significant underabundances relative to Si, the
mean [Ar/Si] value being -0.61. No theoretical yields of Ar may explain such
a large underabundance of Ar relative to Si, and the [Ar/Si] ratio is expected
to be only weakly dependent on the SFH undergone by DLAs. Dust depletion
effects are also not likely to explain these underabundances, since Ar is
non-refractory. The only explanation can be found in the ionization effects.
Indeed, Ar I is very sensitive to ionization, in particular because its
photoionization cross-section is one order of magnitude larger than for
H I (Sofia & Jenkins 1998). Hence, Lyman continuum photons with energies
.
Interestingly, all the
obtained Ar measurements show significant underabundances relative to Si, the
mean [Ar/Si] value being -0.61. No theoretical yields of Ar may explain such
a large underabundance of Ar relative to Si, and the [Ar/Si] ratio is expected
to be only weakly dependent on the SFH undergone by DLAs. Dust depletion
effects are also not likely to explain these underabundances, since Ar is
non-refractory. The only explanation can be found in the ionization effects.
Indeed, Ar I is very sensitive to ionization, in particular because its
photoionization cross-section is one order of magnitude larger than for
H I (Sofia & Jenkins 1998). Hence, Lyman continuum photons with energies ![]() Ryd are more efficient in ionizing Ar I than H I, if they
are able to leak through the H I layer (Vladilo et al. 2003). We wish to
emphasize, however, that although all of our DLAs show a significant Ar
underabundance, other ionization diagnostics imply the gas is predominantly
neutral for the majority of our DLAs. Therefore, the [Ar/Si] ratio alone cannot
characterize the ionization fraction of a DLA.
Ryd are more efficient in ionizing Ar I than H I, if they
are able to leak through the H I layer (Vladilo et al. 2003). We wish to
emphasize, however, that although all of our DLAs show a significant Ar
underabundance, other ionization diagnostics imply the gas is predominantly
neutral for the majority of our DLAs. Therefore, the [Ar/Si] ratio alone cannot
characterize the ionization fraction of a DLA.
Ti: Ti is generally accepted as an
![]() -element, because it exhibits abundance patterns similar to other
-element, because it exhibits abundance patterns similar to other
![]() -elements in Galactic stars (Edvardsson et al. 1995; François et al. 2004). It is a
refractory element and has a high dust depletion level, even higher than Fe in
Galactic ISM clouds (Savage & Sembach 1996). The dust depletion effects thus explain
the large dispersion in the [Ti/Si] ratios of 0.33 dex, and the mean value of -0.15 is suggestive of some presence of dust in the majority of DLAs studied.
The large dispersion in the [Ti/Fe] ratios of 0.38 dex is due both to dust
depletion and nucleosynthesis enrichment effects. Positive departures of
[Ti/Fe] from the solar value is evidence of an
-elements in Galactic stars (Edvardsson et al. 1995; François et al. 2004). It is a
refractory element and has a high dust depletion level, even higher than Fe in
Galactic ISM clouds (Savage & Sembach 1996). The dust depletion effects thus explain
the large dispersion in the [Ti/Si] ratios of 0.33 dex, and the mean value of -0.15 is suggestive of some presence of dust in the majority of DLAs studied.
The large dispersion in the [Ti/Fe] ratios of 0.38 dex is due both to dust
depletion and nucleosynthesis enrichment effects. Positive departures of
[Ti/Fe] from the solar value is evidence of an ![]() -enhancement, and
negative [Ti/Fe] ratios provide evidence of dust depletion
(see Dessauges-Zavadsky et al. 2002).
-enhancement, and
negative [Ti/Fe] ratios provide evidence of dust depletion
(see Dessauges-Zavadsky et al. 2002).
Cr, Ni, Fe: Cr, Ni, and Fe are three iron-peak elements with refractory properties. They trace each other in Galactic stars, but in gas phase the [Cr/Fe] and [Ni/Fe] ratios may show small differences from the solar value, due to differential dust depletion. All the DLAs studied show an enhanced [Cr/Fe] ratio, the mean value being +0.13 dex in agreement with Prochaska & Wolfe (2002) findings. This is suggestive of dust depletion, since Galactic ISM lines of sight do exhibit a mild Cr overabundance relative to Fe. However, it is difficult to explain why every DLA shows enhanced [Cr/Fe] and why there is no trend with [Zn/Fe] (for the Zn discussion see below). The mean [Ni/Fe] value is solar, as it is observed in the Galactic ISM. These two abundance ratios show no dispersion, and they are uniform from one DLA to another with an rms of 0.06 and 0.08 dex, respectively. This uniformity can be explained by the fact that Cr, Ni, and Fe have very similar dust depletion patterns in the Galactic ISM (Savage & Sembach 1996), and the DLAs do not have enough high dust depletion variations from one system to another to produce [Cr/Fe] and [Ni/Fe] variations.
Mn: Mn is an iron-peak element, but it
behaves differently from other iron-peak elements. The [Mn/Fe] ratios in
Galactic stars are undersolar and show a decrease with metallicity. They
illustrate a nice example of the odd-even effect for iron-nuclei. All the Mn
abundance measurements obtained in the DLAs studied are also underabundant
relative to Fe with a [Mn/Fe] mean value of -0.23. In addition, these
measurements are very uniform with an rms of 0.05 dex. This uniformity implies
two important consequences. Firstly, the DLA [Mn/Fe] ratios reach a plateau at
-0.23 dex with a small scatter for a metallicity of DLA systems between
![]() and -0.7 dex. Secondly, the [Mn/Fe] ratios are similar
irrespective of the dust depletion level of DLAs, as we have already argued in
Dessauges-Zavadsky et al. (2002), since Mn has a very similar dust depletion level to that
of Fe. In a future paper, we will consider if this result contradicts the
conclusions of McWilliam et al. (2003) based on stellar abundances that Mn is a
secondary element.
and -0.7 dex. Secondly, the [Mn/Fe] ratios are similar
irrespective of the dust depletion level of DLAs, as we have already argued in
Dessauges-Zavadsky et al. (2002), since Mn has a very similar dust depletion level to that
of Fe. In a future paper, we will consider if this result contradicts the
conclusions of McWilliam et al. (2003) based on stellar abundances that Mn is a
secondary element.
Table 10: Abundance patterns and correlations between [X/Y] ratios and [Zn/Fe] for all clouds observed in our sample of 11 DLAs.
Co: We obtained the third Co abundance
measurement in the DLA system toward Q1157+014. The first ones were obtained by
Ellison et al. (2001) and Rao et al. (2005). Co is an iron-peak element. Its dust
depletion in the Galactic ISM is not well known; Co has probably a refractory
nature similar to the one of Fe. In Galactic stars, [Co/Fe] shows a large
scatter around the solar value. No general DLA abundance pattern trend can be
discussed for this element yet. The three [Co/Fe] measurements are:
![]() (our value),
(our value),
![]() (Ellison et al. 2001), and
(Ellison et al. 2001), and
![]() (Rao et al. 2005).
(Rao et al. 2005).
Zn: Zn is an extremely important element in
DLA abundance studies. It is frequently considered as an iron-peak element
because it traces the other iron-peak elements in Galactic stars, but Zn is
probably produced through different nucleosynthetic processes
(e.g. Matteucci et al. 1993). Zn has a unique trump, which is that it is not
readily incorporated into dust grains and thus is only very mildly refractory
(Savage & Sembach 1996). As a consequence, the [Zn/Fe] ratio is widely used as a
tracer of the dust depletion level in a DLA, with higher [Zn/Fe] values
implying higher depletion levels. Our measurements show a high dispersion of
0.22 dex in the [Zn/Fe] ratios and a reduced ![]() of 26. The [Zn/Fe] values
vary from 0 to +0.8, which indicates that the DLAs studied sample a relatively
large range of dust depletion levels. The [Zn/Si] ratio is relatively free from
dust depletion effects, since, as discussed above, the refractory
of 26. The [Zn/Fe] values
vary from 0 to +0.8, which indicates that the DLAs studied sample a relatively
large range of dust depletion levels. The [Zn/Si] ratio is relatively free from
dust depletion effects, since, as discussed above, the refractory
![]() -element Si traces the volatile element S well whatever the dust
depletion level might be in the DLAs studied. Hence, the [Zn/Si] ratio is a good
tracer of only nucleosynthetic enrichment. The [Zn/Si] dispersion of 0.17 dex
with a
-element Si traces the volatile element S well whatever the dust
depletion level might be in the DLAs studied. Hence, the [Zn/Si] ratio is a good
tracer of only nucleosynthetic enrichment. The [Zn/Si] dispersion of 0.17 dex
with a
![]() of 10 is relatively large, and its most straightforward
explanation can be found in different SFHs from one DLA to another. However,
this dispersion, as well as the mean solar [Zn/Si] value, contradict the
results obtained for [Si/Fe] and [S/Fe]. Indeed, as discussed above,
the [Si/Fe] and [S/Fe] ratios seem to be uniform and enhanced relative to solar
values. How can we reconcile the solar [Zn/Si] abundance pattern with the
of 10 is relatively large, and its most straightforward
explanation can be found in different SFHs from one DLA to another. However,
this dispersion, as well as the mean solar [Zn/Si] value, contradict the
results obtained for [Si/Fe] and [S/Fe]. Indeed, as discussed above,
the [Si/Fe] and [S/Fe] ratios seem to be uniform and enhanced relative to solar
values. How can we reconcile the solar [Zn/Si] abundance pattern with the
![]() -enhancement observed in the [Si/Fe] and [S/Fe] ratios that cannot
entirely be accounted for by dust depletion effects? The only solution is to
assume that the [Zn/Fe] ratio can be larger than 0, independently from dust
depletion effects. Recent measurements of Galactic metal-poor stars indeed
suggest that Zn is overabundant relative to Fe in the range of 0 to +0.2 dex
for metallicities between
-enhancement observed in the [Si/Fe] and [S/Fe] ratios that cannot
entirely be accounted for by dust depletion effects? The only solution is to
assume that the [Zn/Fe] ratio can be larger than 0, independently from dust
depletion effects. Recent measurements of Galactic metal-poor stars indeed
suggest that Zn is overabundant relative to Fe in the range of 0 to +0.2 dex
for metallicities between
![]() and -1
(François et al. 2004; Prochaska & McWilliam 2000; Chen et al. 2004; Mishenina et al. 2002; Nissen et al. 2004).
and -1
(François et al. 2004; Prochaska & McWilliam 2000; Chen et al. 2004; Mishenina et al. 2002; Nissen et al. 2004).
Ge: Ge is the element with the highest
atomic number (Z = 32) for which we obtained an abundance measurement.
Prochaska et al. (2003) were the first to draw attention to the prospect of
measuring Ge in DLAs. It is an element of the iron-peak, but the s-process in
massive stars may also contribute to its production. It thus has a secondary
origin, since it can only be produced when Fe is already present in stars.
Cowan et al. (2005) have very recently shown that Ge abundances in Galactic
metal-poor stars track the Fe abundances very well, but at a depressed level,
![]() [Ge/Fe]
[Ge/Fe]
![]() .
Hence, an explosive process on
iron-peak nuclei, rather than neutron capture, appears to be the dominant
synthesis mechanism for Ge at low metallicities. At higher metallicities, the
s-process production takes place, and it would be expected that the Ge
abundances would increase with the Fe abundances. In DLAs, the Ge abundances do
not seem to follow the same trend relative to the Fe abundances. Indeed, the
two measured [Ge/Fe] abundance ratios are oversolar, [Ge/Fe]
.
Hence, an explosive process on
iron-peak nuclei, rather than neutron capture, appears to be the dominant
synthesis mechanism for Ge at low metallicities. At higher metallicities, the
s-process production takes place, and it would be expected that the Ge
abundances would increase with the Fe abundances. In DLAs, the Ge abundances do
not seem to follow the same trend relative to the Fe abundances. Indeed, the
two measured [Ge/Fe] abundance ratios are oversolar, [Ge/Fe]
![]() (our measurement) and [Ge/Fe] = +0.77 (Prochaska et al. 2003).
(our measurement) and [Ge/Fe] = +0.77 (Prochaska et al. 2003).
B, As, Kr: We just obtained upper limits to the abundances of these elements. They will be discussed in a future paper.
From the Voigt profile fitting of metal-lines, we obtained very accurate component-to-component column density measurements. These components presumably correspond to interstellar medium clouds in the DLA galaxy on the QSO line of sight. We consider here these clouds as individual entities and study their abundance pattern trends.
It is important, however, to define the concept of a cloud more strictly
relative to the components defined in the Voigt profile fits. Indeed, to be
able to consider the column density of a component as a physical property of an
individual ISM cloud on a QSO line of sight, the component has to be
independent, i.e. unblended with its neighbors. We assumed two components are
independent if they satisfy the following criterion: the difference of position, ![]() ,
in velocity space between two components has to be larger than the
sum of their half line widths (i.e. their half b-values) within 5
,
in velocity space between two components has to be larger than the
sum of their half line widths (i.e. their half b-values) within 5![]() of their respective errors. The results of this criterion agree well with an
eye-ball determination of independent components from optical
depth considerations. The components which do not satisfy this criterion are
encompassed in Tables 2-8 and together they
form an independent cloud. Their column densities have to be summed and
this sum corresponds to the column density of the cloud. The same criterion has
been applied to the DLAs studied in Paper I. In our sample of 11 DLA systems,
we find a total of 84 clouds.
of their respective errors. The results of this criterion agree well with an
eye-ball determination of independent components from optical
depth considerations. The components which do not satisfy this criterion are
encompassed in Tables 2-8 and together they
form an independent cloud. Their column densities have to be summed and
this sum corresponds to the column density of the cloud. The same criterion has
been applied to the DLAs studied in Paper I. In our sample of 11 DLA systems,
we find a total of 84 clouds.
In the first part of Table 10, we present the dispersion
properties for different abundance ratios - [Si/Fe], [S/Fe], [Si/Zn], [S/Zn],
[S/Si], [N/Si], [Mn/Fe], [Cr/Fe], and [Zn/Fe] - of all the clouds observed in
our sample of 11 DLA galaxies. We give the logarithmic weighted mean computed
using the 1![]() errors as weights in Col. (3), the logarithmic rms
dispersion in Col. (4), and the reduced
errors as weights in Col. (3), the logarithmic rms
dispersion in Col. (4), and the reduced ![]() relative to the weighted
mean in Col. (5). We notice that, in general, the mean abundance ratio
values of clouds are very similar to those of integrated profiles of DLAs, but
the measured rms dispersions and reduced
relative to the weighted
mean in Col. (5). We notice that, in general, the mean abundance ratio
values of clouds are very similar to those of integrated profiles of DLAs, but
the measured rms dispersions and reduced ![]() are 2-3 times larger for
individual clouds than the values obtained for the DLAs
(see Table 9). This is partly due to the larger statistical
errors in the cloud abundance ratio measurements.
are 2-3 times larger for
individual clouds than the values obtained for the DLAs
(see Table 9). This is partly due to the larger statistical
errors in the cloud abundance ratio measurements.
However, we do observe statistically significant dispersions of about
5![]() in the [Zn/Fe] ratio and larger than 3
in the [Zn/Fe] ratio and larger than 3![]() in the
[
in the
[![]() /Fe,Zn] ratios, except for [S/Zn] which has a particularly low
dispersion
/Fe,Zn] ratios, except for [S/Zn] which has a particularly low
dispersion![]() .
High dispersions are expected according to the observations made in the Milky
Way and the Local Group galaxies, if these clouds probe different physical
conditions and come from galaxies with various SFHs. Indeed, the observed
gas-phase abundance ratios along a Galactic line of sight may vary by more than
0.5 dex as the sightline penetrates clouds arising in various phases of the ISM
(e.g. Savage & Sembach 1996). Similarly, the LMC and SMC also exhibit large
variations in their gas-phase abundance ratios (Welty et al. 2001,1999). This is
due to the fact that sightlines through the ISM probe gas with a range of
physical conditions, e.g. various dust-to-gas ratios, volume densities, and
ionization states. In addition, a range of at least 0.3 dex in the
.
High dispersions are expected according to the observations made in the Milky
Way and the Local Group galaxies, if these clouds probe different physical
conditions and come from galaxies with various SFHs. Indeed, the observed
gas-phase abundance ratios along a Galactic line of sight may vary by more than
0.5 dex as the sightline penetrates clouds arising in various phases of the ISM
(e.g. Savage & Sembach 1996). Similarly, the LMC and SMC also exhibit large
variations in their gas-phase abundance ratios (Welty et al. 2001,1999). This is
due to the fact that sightlines through the ISM probe gas with a range of
physical conditions, e.g. various dust-to-gas ratios, volume densities, and
ionization states. In addition, a range of at least 0.3 dex in the ![]() /Fe
abundance ratios is observed both within a galaxy and from galaxy to galaxy
when comparing the abundance measurements of stars in the Milky Way with those
in the Magellanic Clouds and dwarf spheroidal galaxies
(Venn 1999; Tolstoy et al. 2003; Shetrone et al. 2003). Thus, the observed dispersion in the DLA
cloud-to-cloud abundance ratios suggests at first glance that the individual
clouds do not have a similar enrichment history or a uniform differential dust
depletion. Moreover, the fact that this dispersion is higher than the one of
global DLA abundance measurements indicates that the SFH, dust, and ionization
variations are confined more to individual clouds rather than to the whole DLA
galaxy. If confirmed, this will provide important constraints on the
understanding of the ISM of high-redshift galaxies and the enrichment of gas in
the early Universe. In Sect. 6 we study the cloud-to-cloud
variations further within a given DLA system.
/Fe
abundance ratios is observed both within a galaxy and from galaxy to galaxy
when comparing the abundance measurements of stars in the Milky Way with those
in the Magellanic Clouds and dwarf spheroidal galaxies
(Venn 1999; Tolstoy et al. 2003; Shetrone et al. 2003). Thus, the observed dispersion in the DLA
cloud-to-cloud abundance ratios suggests at first glance that the individual
clouds do not have a similar enrichment history or a uniform differential dust
depletion. Moreover, the fact that this dispersion is higher than the one of
global DLA abundance measurements indicates that the SFH, dust, and ionization
variations are confined more to individual clouds rather than to the whole DLA
galaxy. If confirmed, this will provide important constraints on the
understanding of the ISM of high-redshift galaxies and the enrichment of gas in
the early Universe. In Sect. 6 we study the cloud-to-cloud
variations further within a given DLA system.
![\begin{figure}
\par\includegraphics[width=15cm,clip]{3200fig23.ps}
\end{figure}](/articles/aa/full/2006/01/aa3200-05/Timg108.gif) |
Figure 16:
Eight different abundance ratios [X/Y] versus [Zn/Fe] for the entire
set of clouds observed in our sample of 11 DLAs. The Kendall test shows clear
correlations between [Si/Fe], [S/Fe], [Si/Zn], [S/Zn], [S/Si], and [Zn/Fe] with
a probability under the null hypothesis of zero correlation, P( |
| Open with DEXTER | |
In the second part of Table 10, we present the results of
our study on different possible correlations between an abundance ratio [X/Y]
and [Zn/Fe]. The [Zn/Fe] ratio is considered as a dust depletion indicator (see
Sect. 4). A few of these correlations have already been explored
by e.g. Prochaska & Wolfe (2002) for the abundance measurements obtained in DLAs,
but this is the first time that we probe such properties for the individual
clouds within DLAs. The trend discussed above that SFH/dust/ionization
variations are likely to be more confined to individual clouds than to the
global DLA galaxies suggests that if some correlations exist between some
physical properties, they should be more easily identified in individual cloud
studies. We searched for correlations between [Zn/Fe] and the nucleosynthesis
indicators [Si/Fe], [S/Fe], [Si/Zn], [S/Zn], [N/Si], and [Mn/Fe], and between
[Zn/Fe] and other dust depletion indicators [S/Si] and [Cr/Fe]. A Kendall test
was performed to analyze these correlations, and in Col. (7) we give the
Kendall correlation factor ![]() and in Col. (8) the probability P(
and in Col. (8) the probability P(![]() )
under the null hypothesis of zero correlation (values lower than 5% indicate
a significant correlation). In Cols. (9) and (10), we report the zero points
and slopes with their 1
)
under the null hypothesis of zero correlation (values lower than 5% indicate
a significant correlation). In Cols. (9) and (10), we report the zero points
and slopes with their 1![]() errors of the linear least-square regressions,
[X/Y] = a + b
errors of the linear least-square regressions,
[X/Y] = a + b ![]() [Zn/Fe], computed for the cases of significant
correlations. The errors on both [X/Y] and [Zn/Fe] ratios were taken into
account in this computation. We have not, however, accounted for the fact that
Zn or Fe are generally present in the ratios along each axis (i.e. [Zn/Fe] and
[X/Y]). Therefore, one should be more skeptical of correlations with less than 99% significance.
[Zn/Fe], computed for the cases of significant
correlations. The errors on both [X/Y] and [Zn/Fe] ratios were taken into
account in this computation. We have not, however, accounted for the fact that
Zn or Fe are generally present in the ratios along each axis (i.e. [Zn/Fe] and
[X/Y]). Therefore, one should be more skeptical of correlations with less than 99% significance.
Figure 16 shows that there are clear correlations
between [Si/Fe] and [S/Fe] versus [Zn/Fe] and clear anti-correlations between
[Si/Zn] and [S/Zn] versus [Zn/Fe]. These trends are the result of a
combination of dust depletion and nucleosynthesis enrichment effects. But, more
precisely, the increase of the [![]() /Fe] ratios and the decrease of the
[Si/Zn] ratio with the dust depletion level can mainly be assigned to
differential dust depletion effects. The nucleosynthesis enrichment effects
contribute only negligibly to the strength of the evolution as a function of
dust depletion, as illustrated by [S/Zn] versus [Zn/Fe]. Indeed, the [S/Zn]
ratio, which is independent of dust depletion effects, is an intrinsic tracer
of nucleosynthesis enrichment, and the correlation between [S/Zn] and [Zn/Fe]
is observed at only 95% confidence level, and the slope of its linear
least-square regression is consistent with zero (
/Fe] ratios and the decrease of the
[Si/Zn] ratio with the dust depletion level can mainly be assigned to
differential dust depletion effects. The nucleosynthesis enrichment effects
contribute only negligibly to the strength of the evolution as a function of
dust depletion, as illustrated by [S/Zn] versus [Zn/Fe]. Indeed, the [S/Zn]
ratio, which is independent of dust depletion effects, is an intrinsic tracer
of nucleosynthesis enrichment, and the correlation between [S/Zn] and [Zn/Fe]
is observed at only 95% confidence level, and the slope of its linear
least-square regression is consistent with zero (
![]() ).
This analysis, in addition, suggests that the high dispersion observed in the
[Si/Fe], [S/Fe], and [Si/Zn] ratios (see the first part of
Table 10) is the result of only dust depletion effects. The
nucleosynthesis enrichment effects are, indeed, negligible given the low
dispersion measured in the [S/Zn] ratio and the low dispersion of [Si/Fe],
[S/Fe], and [Si/Zn] along the linear least-square regressions (see
Fig. 16). Consequently, the individual clouds very
likely have a similar enrichment history, but different dust depletion levels.
).
This analysis, in addition, suggests that the high dispersion observed in the
[Si/Fe], [S/Fe], and [Si/Zn] ratios (see the first part of
Table 10) is the result of only dust depletion effects. The
nucleosynthesis enrichment effects are, indeed, negligible given the low
dispersion measured in the [S/Zn] ratio and the low dispersion of [Si/Fe],
[S/Fe], and [Si/Zn] along the linear least-square regressions (see
Fig. 16). Consequently, the individual clouds very
likely have a similar enrichment history, but different dust depletion levels.
The signature of pure nucleosynthesis contribution (i.e. of the SFH) can be
observed in the values of the [![]() /Fe,Zn] ratios at [Zn/Fe]
/Fe,Zn] ratios at [Zn/Fe] ![]() .
Indeed, at
.
Indeed, at
![]() ,
the dust depletion level is low, and hence the
,
the dust depletion level is low, and hence the
![]() -element over iron-peak element ratios are free from dust depletion
effects. We computed the weighted means of data points contained in the
interval [Zn/Fe]
= [0,+0.2] (see the dotted boxes in
Fig. 16), and interestingly we find enhanced
[
-element over iron-peak element ratios are free from dust depletion
effects. We computed the weighted means of data points contained in the
interval [Zn/Fe]
= [0,+0.2] (see the dotted boxes in
Fig. 16), and interestingly we find enhanced
[![]() /Fe,Zn] ratios relative to solar in all cases:
/Fe,Zn] ratios relative to solar in all cases:
![]() [Si/Fe]
[Si/Fe]
![]() ,
,
![]() [S/Fe]
[S/Fe]
![]() ,
,
![]() [Si/Zn]
[Si/Zn]
![]() ,
and
,
and ![]() [S/Zn]
[S/Zn]
![]() .
This suggests that the intrinsic abundance patterns of
individual clouds within DLAs, when the nucleosynthesis enrichment can reliably
be disentangled from dust depletion effects, show an
.
This suggests that the intrinsic abundance patterns of
individual clouds within DLAs, when the nucleosynthesis enrichment can reliably
be disentangled from dust depletion effects, show an ![]() -enhancement
indicative of type II SNe. We would like, in addition, to underline the
relatively important difference which exists between the mean [Si/Fe] ratio and
the mean [S/Zn] ratio, yet measured in the same clouds free from dust depletion
effects. The fact that [S/Zn] is almost solar, while [Si/Fe] shows a clear
-enhancement
indicative of type II SNe. We would like, in addition, to underline the
relatively important difference which exists between the mean [Si/Fe] ratio and
the mean [S/Zn] ratio, yet measured in the same clouds free from dust depletion
effects. The fact that [S/Zn] is almost solar, while [Si/Fe] shows a clear
![]() -enhancement, suggests that the [S/Zn] ratio, although independent from
dust depletion effects, may not be a reliable tracer of nucleosynthesis
enrichment as considered until now (e.g. Centurión et al. 2000). Indeed, the S production is perhaps correlated in some way with the production of Zn
(see Fenner et al. 2004).
-enhancement, suggests that the [S/Zn] ratio, although independent from
dust depletion effects, may not be a reliable tracer of nucleosynthesis
enrichment as considered until now (e.g. Centurión et al. 2000). Indeed, the S production is perhaps correlated in some way with the production of Zn
(see Fenner et al. 2004).
Some of the correlations and anti-correlations found in this analysis of clouds
within DLAs have already been observed in DLAs themselves (e.g. [Si/Fe] versus
[Zn/Fe]), while for some we observe only trends due to fewer data points.
Similarly, the ![]() -enhanced abundance pattern unambiguously observed in
individual clouds is still being debated for the global DLA abundance patterns
(Vladilo 1998; Prochaska & Wolfe 2002; Vladilo 2002; Centurión et al. 2000). We stressed this issue in
Sect. 4 with the mean DLA [Si,S/Fe] ratios showing an
-enhanced abundance pattern unambiguously observed in
individual clouds is still being debated for the global DLA abundance patterns
(Vladilo 1998; Prochaska & Wolfe 2002; Vladilo 2002; Centurión et al. 2000). We stressed this issue in
Sect. 4 with the mean DLA [Si,S/Fe] ratios showing an
![]() -enhancement and the mean [Si/Zn] ratios showing solar values.
-enhancement and the mean [Si/Zn] ratios showing solar values.
We also explored the correlations of [Zn/Fe] with two other nucleosynthesis
enrichment indicators, [N/Si] and [Mn/Fe]. No clear correlation was observed for
any of these ratios (see Fig. 16). This is particularly
interesting in the case of [Mn/Fe], since it shows that all the clouds have
an undersolar [Mn/Fe] ratio, irrespective of dust depletion level, except for
the dustiest cloud with
![]() .
Hence, this underabundance is only a
result of nucleosynthesis enrichment. Evidence of intrinsic subsolar [Mn/Fe]
abundances in DLAs themselves were discussed in Sect. 4.
.
Hence, this underabundance is only a
result of nucleosynthesis enrichment. Evidence of intrinsic subsolar [Mn/Fe]
abundances in DLAs themselves were discussed in Sect. 4.
Finally, we found an interesting correlation between [Zn/Fe] and the ratio of
two ![]() -elements: S, a volatile element, and Si, a refractory element (see
Fig. 16). This correlation is a direct result of pure
differential dust depletion effects observed in two
-elements: S, a volatile element, and Si, a refractory element (see
Fig. 16). This correlation is a direct result of pure
differential dust depletion effects observed in two ![]() -elements and two
iron-peak elements. The mean value of the [S/Si] ratio in the interval
-elements and two
iron-peak elements. The mean value of the [S/Si] ratio in the interval
![]() is solar,
is solar, ![]() [S/Si]
[S/Si]
![]() ,
which shows that
S traces Si in the presence of a weak dust depletion level.
,
which shows that
S traces Si in the presence of a weak dust depletion level.
Table 11: Cloud-to-cloud chemical variation analysis in individual DLA systems.
There are three possible sources of abundance variations among clouds: (i) different nucleosynthesis enrichments, i.e. different star formation histories from cloud-to-cloud; (ii) different dust depletion levels, i.e. different dust amounts and/or physical conditions from cloud-to-cloud; and (iii) different ionization conditions, i.e. different densities (self-shielding) and/or ionizing fluxes from cloud-to-cloud. Each of these three sources can be tested with specific abundance ratios (see Sect. 1). Analyzing these specific abundance ratios in a given DLA galaxy, we tried to determine the sources leading to cloud-to-cloud variations within a DLA galaxy.
In Table 11 we describe the different abundance ratios
analyzed and the number of clouds observed within each DLA. [Si/Fe] is the
only abundance ratio for which a measurement is obtained in all the clouds
along a given QSO sightline. In Cols. (4)-(6) we give the first
simple statistical results for the cloud-to-cloud abundance variations, namely
the logarithmic weighted mean computed using the 1![]() errors as weights,
the logarithmic rms dispersion, and the reduced
errors as weights,
the logarithmic rms dispersion, and the reduced ![]() relative to the
weighted mean, respectively. In addition, we performed a series of Monte-Carlo
simulations, using the technique designed by Prochaska (2003), to
investigate the deviations allowed within each DLA and to derive quantitative
limits and values of the cloud-to-cloud variations relative to the weighted
mean. This technique consists of making three measures of the uniformity within
individual DLAs. With one measure, we study an extreme scenario where all of
the variation arises from a single cloud. In Col. (7) we give the values of
relative to the
weighted mean, respectively. In addition, we performed a series of Monte-Carlo
simulations, using the technique designed by Prochaska (2003), to
investigate the deviations allowed within each DLA and to derive quantitative
limits and values of the cloud-to-cloud variations relative to the weighted
mean. This technique consists of making three measures of the uniformity within
individual DLAs. With one measure, we study an extreme scenario where all of
the variation arises from a single cloud. In Col. (7) we give the values of
![]() ,
the minimum [X/Y] variation in a single cloud, which gives
,
the minimum [X/Y] variation in a single cloud, which gives
![]() in over 95% of the 1000 trials in the
Monte-Carlo analysis. The two other measures assume deviations in all the
clouds with values drawn from a uniform distribution. In Cols. (8) and (9) we
calculate, respectively,
in over 95% of the 1000 trials in the
Monte-Carlo analysis. The two other measures assume deviations in all the
clouds with values drawn from a uniform distribution. In Cols. (8) and (9) we
calculate, respectively,
![]() ,
the minimum variation which when
applied to every cloud gives
,
the minimum variation which when
applied to every cloud gives
![]() in over 95% of the trials, and
in over 95% of the trials, and
![]() ,
the variation which when applied to
each cloud has the highest probability of yielding
,
the variation which when applied to
each cloud has the highest probability of yielding
![]() %. The
%. The
![]() values are the most realistic
upper limits to abundance variations and
values are the most realistic
upper limits to abundance variations and
![]() reflects the most
likely value (for more details, see Prochaska 2003).
reflects the most
likely value (for more details, see Prochaska 2003).
![\begin{figure}
\par\includegraphics[width=7cm,clip]{3200fig24.ps}
\end{figure}](/articles/aa/full/2006/01/aa3200-05/Timg126.gif) |
Figure 17:
Cloud-to-cloud [X/Y] abundance ratios in the DLA toward Q0450-13.
A total number of 11 clouds covering 232 km s-1 in velocity space are
detected in this DLA along the QSO line of sight. The dashed line corresponds
to the logarithmic weighted mean of the cloud-to-cloud [X/Y] ratios computed
by using their 1 |
| Open with DEXTER | |
We performed the cloud-to-cloud chemical variation analysis only in the DLA systems in which the majority of the abundance ratios considered can be measured in at least three clouds. For this reason, the DLAs toward Q0841+129, Q2348-1444, and Q0100+13 were excluded. We now briefly discuss the cloud-to-cloud abundance ratios for the seven remaining DLAs studied. For each analyzed DLA, we plot the cloud-to-cloud abundance ratios as a function of the velocity of the clouds.
![\begin{figure}
\par\includegraphics[width=7cm,clip]{3200fig25.ps}
\end{figure}](/articles/aa/full/2006/01/aa3200-05/Timg127.gif) |
Figure 18: Same as Fig. 17 for the DLA toward Q1157+014. A total number of 4 clouds covering 144 km s-1 in velocity space are detected in this DLA along the QSO line of sight. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7cm,clip]{3200fig26.ps}
\end{figure}](/articles/aa/full/2006/01/aa3200-05/Timg128.gif) |
Figure 19: Same as Fig. 17 for the DLA toward Q1331+17 from the first sample of DLAs (see Paper I). A total number of 4 clouds covering 89 km s-1 in velocity space are detected in this DLA along the QSO line of sight. |
| Open with DEXTER | |
DLA toward Q0450-13. Figure 17
shows the cloud-to-cloud abundance ratios of this DLA. A large variation, larger
than 0.2 dex, was observed in all the relative abundances analyzed in this DLA
(see Table 11). The most impressive is the cloud-to-cloud
variation of the [O/Si] ratio observed at 10![]() with
with
![]() dex. It most likely results from a high variation in the ionization level
from cloud-to-cloud. In the clouds at v > +30 km s-1, we observe solar
[O/Si] ratios and in the clouds around -90 km s-1, the [O/Si] ratio is
highly undersolar reaching -1.5 dex and indicating a high ionization level.
The presence of strong ionization signatures in this DLA was already pointed
out in Sect. 3.1 with the detection of strong intermediate-ion
lines, Fe III and N II. The deviation from uniformity observed in
the other abundance ratios with
dex. It most likely results from a high variation in the ionization level
from cloud-to-cloud. In the clouds at v > +30 km s-1, we observe solar
[O/Si] ratios and in the clouds around -90 km s-1, the [O/Si] ratio is
highly undersolar reaching -1.5 dex and indicating a high ionization level.
The presence of strong ionization signatures in this DLA was already pointed
out in Sect. 3.1 with the detection of strong intermediate-ion
lines, Fe III and N II. The deviation from uniformity observed in
the other abundance ratios with
![]() dex is very interesting,
all the more since a similar trend of increasing abundance ratios from bluer
to redder clouds is observed. The fact that this trend is particularly
pronounced in the [N/Si] ratio with a 3
dex is very interesting,
all the more since a similar trend of increasing abundance ratios from bluer
to redder clouds is observed. The fact that this trend is particularly
pronounced in the [N/Si] ratio with a 3![]() variation confirms that it is
due to a variation in the ionization level from cloud-to-cloud, and it provides
constraints on the geometry of the ionizing flux in this DLA galaxy (see
further details in Paper IV).
variation confirms that it is
due to a variation in the ionization level from cloud-to-cloud, and it provides
constraints on the geometry of the ionizing flux in this DLA galaxy (see
further details in Paper IV).
DLA toward Q1157+014. In Fig. 18
we show the cloud-to-cloud abundance ratio plots for this DLA. The [Si/Fe]
and [Mg/Si] ratios are perfectly uniform, while [Zn/Fe] and [Si/Zn] show
variations at the 3![]() level (see Table 11). This
variation is mainly due to one cloud at -32 km s-1 that has a lower
[Zn/Fe] value and a higher [Si/Zn] value than the other two clouds with [Zn/Fe]
and [Si/Zn] measurements. A careful examination of the Zn II,
Fe II, and Si II profiles of this DLA already suggests some clues
for variation. Indeed, the optical depth of component 3 (corresponding to
the cloud at -32 km s-1) is much deeper in the Fe II and
Si II lines than in the Zn II lines in comparison with the redder
components. This variation can be assigned to a dust depletion variation from
cloud-to-cloud. Indeed, the deeper Fe II and Si II optical depths
in the cloud at -32 km s-1 indicate a lower dust amount. As a
consequence, the abundances of Fe and Si, two refractory elements, are not
depleted relative to Zn, a volatile element, in this cloud, while they are
depleted in the clouds at -5 and +31 km s-1, in which we measure an
enhanced [Zn/Fe] ratio and a low [Si/Zn] ratio.
level (see Table 11). This
variation is mainly due to one cloud at -32 km s-1 that has a lower
[Zn/Fe] value and a higher [Si/Zn] value than the other two clouds with [Zn/Fe]
and [Si/Zn] measurements. A careful examination of the Zn II,
Fe II, and Si II profiles of this DLA already suggests some clues
for variation. Indeed, the optical depth of component 3 (corresponding to
the cloud at -32 km s-1) is much deeper in the Fe II and
Si II lines than in the Zn II lines in comparison with the redder
components. This variation can be assigned to a dust depletion variation from
cloud-to-cloud. Indeed, the deeper Fe II and Si II optical depths
in the cloud at -32 km s-1 indicate a lower dust amount. As a
consequence, the abundances of Fe and Si, two refractory elements, are not
depleted relative to Zn, a volatile element, in this cloud, while they are
depleted in the clouds at -5 and +31 km s-1, in which we measure an
enhanced [Zn/Fe] ratio and a low [Si/Zn] ratio.
DLAs toward Q1210+17 and Q2230+02. For these
DLAs, we do not show the cloud-to-cloud abundance ratio plots, because all their
relative abundances are uniform to better than 0.1 dex (see
Table 11). This reveals an important characteristic of these
two high-redshift galaxies: the gas clouds which comprise these galaxies
apparently have very similar physical properties (mainly when considering the
differential dust depletion) and nucleosynthetic enrichment histories. Only the
[O/Si] ratio in the DLA toward Q2230+02 seems to show a 3![]() departure
from uniformity. This may indicate a variation in the ionization properties
within this DLA galaxy, between the cloud observed at -147 km s-1 which
appears to be more ionized, and the three clouds observed around +180 km s-1.
departure
from uniformity. This may indicate a variation in the ionization properties
within this DLA galaxy, between the cloud observed at -147 km s-1 which
appears to be more ionized, and the three clouds observed around +180 km s-1.
DLA toward Q1331+17. In Fig. 19
we show the cloud-to-cloud abundance ratio plots for this DLA. A high variation
in the [Zn/Fe] ratio is observed at more than 7![]() with
with
![]() dex. This variation is due to differential dust depletion variations from
cloud-to-cloud, with the clouds at +38 and +58 km s-1 being less
depleted (having lower [Zn/Fe] ratios) than the clouds at -2 and +18 km s-1. This DLA exhibits, in fact, one of the largest dust depletion level
of any DLA. The presence of a high amount of dust in the clouds at -2 and
+18 km s-1 is also favored by the detections of C0 and Cl0 in
these clouds (see Fig. 4 in Paper I). Indeed, these ions are usually associated
with a dense, cold neutral medium, characteristic of highly depleted gas in the
Milky Way. Furthermore, they generally suggest at least a modest molecular
hydrogen fraction, which is indicative of dust. This strong cloud-to-cloud dust
amount variation is also responsible for variations observed in: (i) [Si/Fe],
with Fe being more depleted than Si; (ii) [Si/Zn], with Si being more
depleted than the very mildly refractory Zn; (iii) [Cr/Fe], with Fe being more
depleted than Cr; and (iv) [S/Si], with Si being more depleted than the
volatile S. Different SFHs from cloud-to-cloud do not seem to contribute to the
[Si/Fe] and [Si/Zn] variations, since the [S/Zn] ratio is perfectly uniform.
Interestingly, the [S/Zn] ratio is almost solar in all clouds, even though
dex. This variation is due to differential dust depletion variations from
cloud-to-cloud, with the clouds at +38 and +58 km s-1 being less
depleted (having lower [Zn/Fe] ratios) than the clouds at -2 and +18 km s-1. This DLA exhibits, in fact, one of the largest dust depletion level
of any DLA. The presence of a high amount of dust in the clouds at -2 and
+18 km s-1 is also favored by the detections of C0 and Cl0 in
these clouds (see Fig. 4 in Paper I). Indeed, these ions are usually associated
with a dense, cold neutral medium, characteristic of highly depleted gas in the
Milky Way. Furthermore, they generally suggest at least a modest molecular
hydrogen fraction, which is indicative of dust. This strong cloud-to-cloud dust
amount variation is also responsible for variations observed in: (i) [Si/Fe],
with Fe being more depleted than Si; (ii) [Si/Zn], with Si being more
depleted than the very mildly refractory Zn; (iii) [Cr/Fe], with Fe being more
depleted than Cr; and (iv) [S/Si], with Si being more depleted than the
volatile S. Different SFHs from cloud-to-cloud do not seem to contribute to the
[Si/Fe] and [Si/Zn] variations, since the [S/Zn] ratio is perfectly uniform.
Interestingly, the [S/Zn] ratio is almost solar in all clouds, even though
![]() dex in clouds where [Zn/Fe] is low. This joins the comment
made in Sect. 5 on the use of [S/Zn] as a nucleosynthesis
enrichment indicator.
dex in clouds where [Zn/Fe] is low. This joins the comment
made in Sect. 5 on the use of [S/Zn] as a nucleosynthesis
enrichment indicator.
![\begin{figure}
\par\includegraphics[width=7cm,clip]{3200fig27.ps}
\end{figure}](/articles/aa/full/2006/01/aa3200-05/Timg133.gif) |
Figure 20: Same as Fig. 17 for the DLA toward Q2231-00 from the first sample of DLAs (see Paper I). A total number of 10 clouds covering 161 km s-1 in velocity space are detected in this DLA along the QSO line of sight. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7cm,clip]{3200fig28.ps}
\end{figure}](/articles/aa/full/2006/01/aa3200-05/Timg134.gif) |
Figure 21: Same as Fig. 17 for the DLA toward Q2343+12 from the first sample of DLAs (see Paper I). A total number of 19 clouds covering 355 km s-1 in velocity space are detected in this DLA along the QSO line of sight. |
| Open with DEXTER | |
DLA toward Q2231-00. In
Fig. 20 we show the cloud-to-cloud abundance ratio plots for this
DLA. The departures from uniformity observed in this system are modest, lower
than 0.2 dex (see Table 11). Only the [Zn/Fe] ratio seems to
show a higher variation with
![]() dex and may reflect some
cloud-to-cloud differential dust depletion variations. However, this does not
affect the uniformity of the other abundance ratios strongly. We observe only
a slight effect of a higher dust depletion level in the clouds at -9 and
0 km s-1 compared to the clouds at -97 and -72 km s-1 on the
[Si/Fe] and [S/Si] ratios. No sign of cloud-to-cloud SFH variations is detected,
the [S/Zn] ratio is uniform.
dex and may reflect some
cloud-to-cloud differential dust depletion variations. However, this does not
affect the uniformity of the other abundance ratios strongly. We observe only
a slight effect of a higher dust depletion level in the clouds at -9 and
0 km s-1 compared to the clouds at -97 and -72 km s-1 on the
[Si/Fe] and [S/Si] ratios. No sign of cloud-to-cloud SFH variations is detected,
the [S/Zn] ratio is uniform.
DLA toward Q2343+12. In Fig. 21
we show the cloud-to-cloud abundance ratio plots for this DLA. The possible
variations due to dust depletion and nucleosynthesis enrichment are difficult
to highlight in this system, partly because many elements are detected in three
clouds only (see Table 11). However, we observe high deviations
from uniformity at more than 4![]() with
with
![]() dex in the
cloud-to-cloud [Si/Fe], [O/Si], and [N/Si] ratios. They are likely to be
dominated by ionization variations. Hints of a possible trend from
cloud-to-cloud of higher [Si/Fe] ratios, when [O/Si] is lower resulting from
ionization effects, can be suggested from our measurements. The presence of a
high ionization level in this DLA was already pointed out in Paper I with the
detection of strong intermediate-ion lines, Fe III, N II, and
S III, and will be discussed further in Paper IV.
dex in the
cloud-to-cloud [Si/Fe], [O/Si], and [N/Si] ratios. They are likely to be
dominated by ionization variations. Hints of a possible trend from
cloud-to-cloud of higher [Si/Fe] ratios, when [O/Si] is lower resulting from
ionization effects, can be suggested from our measurements. The presence of a
high ionization level in this DLA was already pointed out in Paper I with the
detection of strong intermediate-ion lines, Fe III, N II, and
S III, and will be discussed further in Paper IV.
In summary, among the seven DLA systems for which we analyzed the cloud-to-cloud
chemical variations, five of them do show statistically significant
cloud-to-cloud variations, namely higher than 0.2 dex (
![]() dex and
dex and
![]() dex) at more than 3
dex) at more than 3![]() ,
for at least two different
abundance ratios. But, only two DLA systems toward Q0450-13 and Q1331+17 show
"extreme'' variations, that is, a higher dispersion than 0.3 dex at more than
7
,
for at least two different
abundance ratios. But, only two DLA systems toward Q0450-13 and Q1331+17 show
"extreme'' variations, that is, a higher dispersion than 0.3 dex at more than
7![]() .
We were able to identify the sources of these variations thanks to
the analysis of specific abundance ratios. These sources are either the
differential dust depletion variations and/or the ionization condition
variations from cloud-to-cloud. But, no evidence for variations due to
different SFHs was highlighted. This suggests that the gas clouds within some
DLA galaxies have different physical properties, namely different dust
depletion and/or ionization levels, but they all seem to show a uniform
nucleosynthetic enrichment history.
.
We were able to identify the sources of these variations thanks to
the analysis of specific abundance ratios. These sources are either the
differential dust depletion variations and/or the ionization condition
variations from cloud-to-cloud. But, no evidence for variations due to
different SFHs was highlighted. This suggests that the gas clouds within some
DLA galaxies have different physical properties, namely different dust
depletion and/or ionization levels, but they all seem to show a uniform
nucleosynthetic enrichment history.
In the Prochaska (2003) study based on a single abundance ratio, mainly
[Si/Fe], only 2 out of 13 DLAs present cloud-to-cloud variations. Our work
already shows a less uniform picture for the ISM of high-redshift DLA galaxies,
since 5 out of 7 DLAs show chemical variations, and all DLAs except one have at
least a high
![]() (>0.2 dex) for one abundance ratio indicating
that there is at least a single cloud with an "abnormal'' abundance.
The main difference between these two studies comes from the fact that in
our chemical variation analysis we considered other abundance ratios than
[Si/Fe] alone. Given that the observed variations seem to mainly be due to dust
depletion and ionization effects, as stated above, they are thus well-detected
in the ratios tracing the dust depletion variations, i.e. [Zn/Fe], and the
ionization variations. Consideration of the [Si/Fe] ratio alone would have
shown variations in only 3 out of 7 DLAs, so that we would have missed
variations in 2 DLA galaxies.
(>0.2 dex) for one abundance ratio indicating
that there is at least a single cloud with an "abnormal'' abundance.
The main difference between these two studies comes from the fact that in
our chemical variation analysis we considered other abundance ratios than
[Si/Fe] alone. Given that the observed variations seem to mainly be due to dust
depletion and ionization effects, as stated above, they are thus well-detected
in the ratios tracing the dust depletion variations, i.e. [Zn/Fe], and the
ionization variations. Consideration of the [Si/Fe] ratio alone would have
shown variations in only 3 out of 7 DLAs, so that we would have missed
variations in 2 DLA galaxies.
Analysis of our sample of damped Ly![]() systems has proved once again
that these systems constitute the best laboratory for studying the chemical
abundances and the interstellar medium properties of high redshift galaxies. We
obtained new comprehensive sets of elemental abundances of seven DLAs in the
redshift range
systems has proved once again
that these systems constitute the best laboratory for studying the chemical
abundances and the interstellar medium properties of high redshift galaxies. We
obtained new comprehensive sets of elemental abundances of seven DLAs in the
redshift range
![]() toward bright quasars. These were derived
from UVES/VLT spectra combined with existing HIRES/Keck spectra. We detected 54
metal-line transitions, and obtained the column density measurements of 30 ions
from 22 elements, - B, C, N, O, Mg, Al, Si, P, S, Cl, Ar, Ti, Cr, Mn, Fe, Co,
Ni, Cu, Zn, Ge, As, Kr. Together with our first sample of four DLAs analyzed in
Paper I, we have a sample of eleven DLA galaxies with uniquely comprehensive
and homogeneous abundance measurements.
toward bright quasars. These were derived
from UVES/VLT spectra combined with existing HIRES/Keck spectra. We detected 54
metal-line transitions, and obtained the column density measurements of 30 ions
from 22 elements, - B, C, N, O, Mg, Al, Si, P, S, Cl, Ar, Ti, Cr, Mn, Fe, Co,
Ni, Cu, Zn, Ge, As, Kr. Together with our first sample of four DLAs analyzed in
Paper I, we have a sample of eleven DLA galaxies with uniquely comprehensive
and homogeneous abundance measurements.
In this paper (II in the series) we were able to study the abundance patterns and the chemical variations of a wide range of elements in the interstellar medium of galaxies outside the Local Group, all for the first time. Chemical variations from DLA galaxy to DLA galaxy and from cloud to cloud in the ISM within a galaxy are expected, if the line of sight to a distant QSO samples regions with different star formation histories and different ISM conditions. This is suggested by observations in the Milky Way, the Small and Large Magellanic Clouds, and dwarf spheroidal galaxies which show chemical variations from galaxy to galaxy and within the galaxy when comparing their stellar and gas-phase abundance patterns. We considered three potential sources of observed abundance variations: the star formation history (nucleosynthesis enrichment), differential dust depletion, and ionization.
Our main results can be summarized as follows:
1) The abundance patterns of the integrated profiles of DLAs show relatively low
rms dispersions, reaching only 2-3 times higher values than the statistical
errors, for the majority of elements. This uniformity is remarkable given that
the quasar sightlines cross gaseous regions with H I column densities
covering an order of magnitude from
![]() to
to
![]() cm-2 and with metallicities ranging from 1/55 to 1/5 solar.
This implies that the respective star formation histories, if ever different,
have conspired to yield one set of relative abundances and that the effects of
nucleosynthesis enrichment, dust depletion, and ionization are negligible. We
discuss the implications of this uniformity element by element. The most
interesting findings are: (i) the [Si/Fe] and [S/Fe] abundance ratios show an
cm-2 and with metallicities ranging from 1/55 to 1/5 solar.
This implies that the respective star formation histories, if ever different,
have conspired to yield one set of relative abundances and that the effects of
nucleosynthesis enrichment, dust depletion, and ionization are negligible. We
discuss the implications of this uniformity element by element. The most
interesting findings are: (i) the [Si/Fe] and [S/Fe] abundance ratios show an
![]() -enhancement irrespective of the dust depletion level of the DLAs
studied; to reconcile this
-enhancement irrespective of the dust depletion level of the DLAs
studied; to reconcile this ![]() -enhancement with the solar [Si/Zn] ratios,
we suggest that the [Zn/Fe] ratios are intrinsically oversolar (independent of
dust depletion effects) as indicated by the recent measurements in
Galactic metal-poor stars; (ii) all the Ar abundance measurements show a
significant underabundance relative to Si; however, the [Ar/Si] ratio alone
cannot characterize the ionization of a DLA, since DLAs with low [Ar/Si] ratios
include cases where other ionization diagnostics imply the gas is predominantly
neutral; (iii) all the Mn abundance measurements are underabundant relative
to Fe irrespective of the dust depletion of the DLAs studied; they reach a
plateau at -0.23 dex; and (iv) we obtained the second abundance measurement
of Ge, an element beyond the iron-peak, in the metal-strong DLA toward
Q1157+014, opening the way to investigation of s-process elements in DLAs.
-enhancement with the solar [Si/Zn] ratios,
we suggest that the [Zn/Fe] ratios are intrinsically oversolar (independent of
dust depletion effects) as indicated by the recent measurements in
Galactic metal-poor stars; (ii) all the Ar abundance measurements show a
significant underabundance relative to Si; however, the [Ar/Si] ratio alone
cannot characterize the ionization of a DLA, since DLAs with low [Ar/Si] ratios
include cases where other ionization diagnostics imply the gas is predominantly
neutral; (iii) all the Mn abundance measurements are underabundant relative
to Fe irrespective of the dust depletion of the DLAs studied; they reach a
plateau at -0.23 dex; and (iv) we obtained the second abundance measurement
of Ge, an element beyond the iron-peak, in the metal-strong DLA toward
Q1157+014, opening the way to investigation of s-process elements in DLAs.
2) From the Voigt profile fitting of metal-lines, we obtained very accurate
component-to-component column density measurements. These components presumably
correspond to interstellar medium clouds in the DLA galaxy on the QSO line of
sight. By considering all the clouds of all the DLAs studied together, we
see a statistically significant dispersion in several abundance ratios, for
example about 5![]() in the [Zn/Fe] ratios and larger than 3
in the [Zn/Fe] ratios and larger than 3![]() in the [
in the [![]() /Fe,Zn] ratios. This indicates that the chemical variations are
more confined to individual clouds within the DLA galaxies rather than to
integrated profiles. If confirmed, this will provide important constraints on
the understanding of the ISM of high-redshift galaxies and the enrichment of
gas in the early Universe. We found unambiguous correlations between [Si/Fe],
[S/Fe], and [S/Si] versus [Zn/Fe], and anti-correlations between [Si/Zn] and
[S/Zn] versus [Zn/Fe]. These trends are primarily the result of differential
dust depletion effects, which are also responsible for the high cloud-to-cloud
abundance ratio dispersion. The signature of the pure nucleosynthesis
enrichment contribution can be observed in the [
/Fe,Zn] ratios. This indicates that the chemical variations are
more confined to individual clouds within the DLA galaxies rather than to
integrated profiles. If confirmed, this will provide important constraints on
the understanding of the ISM of high-redshift galaxies and the enrichment of
gas in the early Universe. We found unambiguous correlations between [Si/Fe],
[S/Fe], and [S/Si] versus [Zn/Fe], and anti-correlations between [Si/Zn] and
[S/Zn] versus [Zn/Fe]. These trends are primarily the result of differential
dust depletion effects, which are also responsible for the high cloud-to-cloud
abundance ratio dispersion. The signature of the pure nucleosynthesis
enrichment contribution can be observed in the [![]() /Fe,Zn] ratios at low
dust depletion levels,
/Fe,Zn] ratios at low
dust depletion levels,
![]() .
It is characterized by an
.
It is characterized by an
![]() -enhancement in the clouds. However, while the [S/Fe], [S/Fe], and
[Si/Zn] ratios are highly
-enhancement in the clouds. However, while the [S/Fe], [S/Fe], and
[Si/Zn] ratios are highly ![]() -enhanced (>0.2 dex), the [S/Zn] ratio
remains almost solar, suggesting that [S/Zn] may not be a reliable tracer of
nucleosynthesis enrichment, the production of S being perhaps in some way
correlated with the one of Zn.
-enhanced (>0.2 dex), the [S/Zn] ratio
remains almost solar, suggesting that [S/Zn] may not be a reliable tracer of
nucleosynthesis enrichment, the production of S being perhaps in some way
correlated with the one of Zn.
3) We analyzed several specific abundance ratios in individual DLA galaxies to
try to determine the origin of cloud-to-cloud chemical variations when observed
in a given DLA galaxy. Study of the cloud-to-cloud chemical variations
within seven individual DLA systems revealed that five of them show
statistically significant variations, higher than 0.2 dex at more than 3![]() .
Two of them show "extreme'' variations with a dispersion higher
than 0.3 dex at more than 7
.
Two of them show "extreme'' variations with a dispersion higher
than 0.3 dex at more than 7![]() .
The sources of these variations are
either the differential dust depletion and/or the ionization effects, while
there is no evidence of variations due to different star formation histories.
This suggests that the gas clouds within DLA galaxies have different physical
properties, but they all seem to show a uniform nucleosynthetic enrichment
history.
.
The sources of these variations are
either the differential dust depletion and/or the ionization effects, while
there is no evidence of variations due to different star formation histories.
This suggests that the gas clouds within DLA galaxies have different physical
properties, but they all seem to show a uniform nucleosynthetic enrichment
history.
At lower redshift (
![]() ), deep imaging shows that DLA galaxies
are a heterogeneous group that exhibits a variety of morphologies and surface
brightnesses. If this is also the case at high redshift, we may have expected
higher dispersions in the DLA abundance ratios. The uniformity observed in the
global gas-phase abundance patterns of DLAs is thus even more surprising.
Perhaps we are penalized by the small number statistics or, more important,
there may be fundamental differences between high and low redshift DLAs. The
results by Kanekar & Chengalur (2003) may be relevant here. Indeed, they derived
estimates of the spin temperature,
), deep imaging shows that DLA galaxies
are a heterogeneous group that exhibits a variety of morphologies and surface
brightnesses. If this is also the case at high redshift, we may have expected
higher dispersions in the DLA abundance ratios. The uniformity observed in the
global gas-phase abundance patterns of DLAs is thus even more surprising.
Perhaps we are penalized by the small number statistics or, more important,
there may be fundamental differences between high and low redshift DLAs. The
results by Kanekar & Chengalur (2003) may be relevant here. Indeed, they derived
estimates of the spin temperature, ![]() ,
in 24 DLAs and found that all
DLAs with high spin temperatures,
,
in 24 DLAs and found that all
DLAs with high spin temperatures,
![]() K, are identified with
dwarf or low surface brightness galaxies, while DLAs with low
K, are identified with
dwarf or low surface brightness galaxies, while DLAs with low ![]() are
associated with large, luminous galaxies. Interestingly, they observed that low
redshift DLAs have both high and low values of
are
associated with large, luminous galaxies. Interestingly, they observed that low
redshift DLAs have both high and low values of ![]() ,
while high redshift
DLAs (
,
while high redshift
DLAs (
![]() )
have preferentially high
)
have preferentially high ![]() .
This result could
help to understand the uniformity observed in the abundance ratios of DLAs in
our sample.
.
This result could
help to understand the uniformity observed in the abundance ratios of DLAs in
our sample.
The uniformity in the nucleosynthesis enrichment observed in the clouds within DLAs is also surprising and poses important constraints on the formation of high-redshift galaxies. Indeed, one very promising scenario that allows us to explain the DLA kinematics is within the CDM hierarchical cosmology and describes a DLA as multiple merging "clumps'' bound to individual dark matter halos (e.g. Haehnelt et al. 1998; Maller et al. 2001). In that scenario, the uniformity of cloud-to-cloud abundance ratios within a DLA galaxy constrains the abundances of all of the protogalactic clumps making up a DLA system. In terms of nucleosynthesis enrichment, this implies the clumps share a similar chemical enrichment pattern. This represents a challenge for the CDM simulations, since those protogalactic clumps which do not share a common gas reservoir and which merge over a large timescale would not be expected to necessarily have a unique enrichment history and be at the same stage of chemical evolution. It remains to be demonstrated whether these clumps really do express very similar nucleosynthetic enrichment patterns with, in addition, very different dust depletions in some cases. This also places strict constraints on the mixing timescales of protogalaxies. Of course, access to the absolute values of metallicities of these clouds would help to confirm these statements. For this, however, we need to measure the H I column densities of individual clouds within a DLA, which is not possible from the current observations.
Acknowledgements
The authors wish to thank everyone working at ESO/Paranal for the high quality of UVES spectra obtained in service mode. M.D.-Z. is supported by the Swiss National Funds and extends special thanks to Professor A. Maeder for continuous encouragement. M.D.-Z. is grateful to the UCO/Lick Observatory for hosting her in Santa Cruz in September 2004, where the layout and main results of this paper were worked out. J.X.P. acknowledges support through the NSF grant AST 03-07824.
Table 2:
Component structure of the
![]() DLA system toward Q0450-13.
DLA system toward Q0450-13.
Table 3:
Component structure of the
![]() DLA system toward Q0841+129.
DLA system toward Q0841+129.
Table 4:
Component structure of the
![]() DLA system toward Q0841+129.
DLA system toward Q0841+129.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{3200fig1.ps}
\end{figure}](/articles/aa/full/2006/01/aa3200-05/Timg145.gif) |
Figure 1:
Normalized UVES spectrum of Q0450-13 showing the DLA Ly |
| Open with DEXTER | |
Table 5:
Component structure of the
![]() DLA system toward Q1157+014.
DLA system toward Q1157+014.
![\begin{figure}
\par\includegraphics[width=16.5cm,clip]{3200fig2.ps}
\end{figure}](/articles/aa/full/2006/01/aa3200-05/Timg147.gif) |
Figure 2:
Velocity plots of the metal line transitions (normalized intensities
shown by dots with 1 |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=16.5cm,clip]{3200fig3.ps}\end{figure}](/articles/aa/full/2006/01/aa3200-05/Timg148.gif) |
Figure 2: continued. |
| Open with DEXTER | |
Table 6:
Component structure of the
![]() DLA system toward Q1210+17.
DLA system toward Q1210+17.
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{3200fig4.ps}
\end{figure}](/articles/aa/full/2006/01/aa3200-05/Timg152.gif) |
Figure 3:
Normalized UVES spectrum of Q0841+129 showing the
|
| Open with DEXTER | |
Table 7:
Component structure of the
![]() DLA system toward Q2230+02.
DLA system toward Q2230+02.
![\begin{figure}
\par\includegraphics[width=16.5cm,clip]{3200fig5.ps}
\end{figure}](/articles/aa/full/2006/01/aa3200-05/Timg154.gif) |
Figure 4:
Same as Fig. 2 for the first DLA toward Q0841+129
at
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=16.5cm,clip]{3200fig6.ps}\end{figure}](/articles/aa/full/2006/01/aa3200-05/Timg155.gif) |
Figure 4: continued. |
| Open with DEXTER | |
Table 8:
Component structure of the
![]() DLA system toward Q2348-1444.
DLA system toward Q2348-1444.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{3200fig7.ps}
\end{figure}](/articles/aa/full/2006/01/aa3200-05/Timg157.gif) |
Figure 5:
Normalized UVES spectrum of Q0841+129 showing the
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=16.5cm,clip]{3200fig8.ps}
\end{figure}](/articles/aa/full/2006/01/aa3200-05/Timg158.gif) |
Figure 6:
Same as Fig. 2 for the second DLA toward Q0841+129
at
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=16.5cm,clip]{3200fig9.ps}\end{figure}](/articles/aa/full/2006/01/aa3200-05/Timg159.gif) |
Figure 6: continued. |
| Open with DEXTER | |
| |
Figure 7:
Normalized UVES spectrum of Q1157+014 showing the DLA blue wing of
the Ly |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=16.5cm,clip]{3200fig11.ps}
\end{figure}](/articles/aa/full/2006/01/aa3200-05/Timg161.gif) |
Figure 8: Same as Fig. 2 for the DLA toward Q1157+014. The zero velocity is fixed at z=1.94377. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=16.5cm,clip]{3200fig12.ps}\end{figure}](/articles/aa/full/2006/01/aa3200-05/Timg162.gif) |
Figure 8: continued. |
| Open with DEXTER | |
| |
Figure 9:
Normalized UVES spectrum of Q1210+17 showing the DLA Ly |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=16.5cm,clip]{3200fig14.ps}
\end{figure}](/articles/aa/full/2006/01/aa3200-05/Timg164.gif) |
Figure 10: Same as Fig. 2 for the DLA toward Q1210+17. The zero velocity is fixed at z=1.89177. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=16.5cm,clip]{3200fig15.ps}\end{figure}](/articles/aa/full/2006/01/aa3200-05/Timg165.gif) |
Figure 10: continued. |
| Open with DEXTER | |
| |
Figure 11:
Normalized UVES spectrum of Q2230+02 showing the DLA Ly |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=16.5cm,clip]{3200fig17.ps}
\end{figure}](/articles/aa/full/2006/01/aa3200-05/Timg167.gif) |
Figure 12: Same as Fig. 2 for the DLA toward Q2230+02. The zero velocity is fixed at z=1.86359. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=16.5cm,clip]{3200fig18.ps}\end{figure}](/articles/aa/full/2006/01/aa3200-05/Timg168.gif) |
Figure 12: continued. |
| Open with DEXTER | |
| |
Figure 13:
Normalized UVES spectrum of Q2348-1444 showing the DLA Ly |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=16.5cm,clip]{3200fig20.ps}
\end{figure}](/articles/aa/full/2006/01/aa3200-05/Timg170.gif) |
Figure 14: Same as Fig. 2 for the DLA toward Q2348-1444. The zero velocity is fixed at z=2.27939. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=16.5cm,clip]{3200fig21.ps}\end{figure}](/articles/aa/full/2006/01/aa3200-05/Timg171.gif) |
Figure 14: continued. |
| Open with DEXTER | |
In the analysis of ionic column densities of damped Ly![]() systems, we
noticed that we derive a systematically lower Ni+ column density measurement
from the Ni II
systems, we
noticed that we derive a systematically lower Ni+ column density measurement
from the Ni II ![]() 1317 line than from the Ni II lines at
1317 line than from the Ni II lines at
![]() ,
1709, 1741, and 1751 Å, when all these lines are
available in the same DLA system. The simplest way to explain this discrepancy
is to call the reliability of the oscillator strength of the
Ni II
,
1709, 1741, and 1751 Å, when all these lines are
available in the same DLA system. The simplest way to explain this discrepancy
is to call the reliability of the oscillator strength of the
Ni II ![]() 1317 line into question. The most recent atomic data
published for the Ni II transitions are summarized in Table A.1.
In this table we see that Morton (1991) atomic data of the
Ni II
1317 line into question. The most recent atomic data
published for the Ni II transitions are summarized in Table A.1.
In this table we see that Morton (1991) atomic data of the
Ni II ![]() 1454, 1709, 1741, 1751 lines have been updated by
Fedchak et al. (2000), while no new measurement of the f-value exists for the
Ni II
1454, 1709, 1741, 1751 lines have been updated by
Fedchak et al. (2000), while no new measurement of the f-value exists for the
Ni II ![]() 1317 line.
1317 line.
Our UVES/VLT spectra, combined with HIRES/Keck spectra, allowed us to observe
the complete sample of Ni II UV transitions in several DLAs with a
resolution and a signal-to-noise ratio sufficient for accurate analysis. We
therefore decided to use these data to derive an astrophysical oscillator
strength of the Ni II ![]() 1317 transition.
1317 transition.
The adopted method to determine this f-value is relatively simple. We assumed
that the component-to-component column densities derived from the Voigt profile
fitting of the Ni II lines at
![]() ,
1709, 1741,
and 1751 Å have to be the same as those derived from the
Ni II
,
1709, 1741,
and 1751 Å have to be the same as those derived from the
Ni II ![]() 1317 line, and we varied the
Ni II
1317 line, and we varied the
Ni II ![]() 1317 f-value by requiring that this line yield the
same component-to-component column densities as the other Ni II lines.
More concretely, we determined the best value of the
Ni II
1317 f-value by requiring that this line yield the
same component-to-component column densities as the other Ni II lines.
More concretely, we determined the best value of the
Ni II ![]() 1317 oscillator strength via a
1317 oscillator strength via a ![]() minimization
of theoretical Voigt profile fits to the observed absorption
Ni II
minimization
of theoretical Voigt profile fits to the observed absorption
Ni II ![]() 1317 line. We fixed the fitting parameters, the
component-to-component b-values and redshifts, to the values of the
best-fitting solution obtained for the low-ion lines, and the
component-to-component Ni+ column densities to the values obtained from the
Voigt profile fitting of Ni II lines other than the
Ni II
1317 line. We fixed the fitting parameters, the
component-to-component b-values and redshifts, to the values of the
best-fitting solution obtained for the low-ion lines, and the
component-to-component Ni+ column densities to the values obtained from the
Voigt profile fitting of Ni II lines other than the
Ni II ![]() 1317 line (see
Tables 2-8).
1317 line (see
Tables 2-8).
We performed this analysis in five DLA systems, in which we detect, with high
accuracy, at least two Ni II lines besides the
Ni II ![]() 1317 line. We do not consider the
Ni II
1317 line. We do not consider the
Ni II ![]() 1370 line in this analysis, since it also seems
to show some discrepancy to the best-fit solution obtained from the
Ni II
1370 line in this analysis, since it also seems
to show some discrepancy to the best-fit solution obtained from the
Ni II ![]() 1454, 1709, 1741, 1751 lines. The five selected DLAs
are the DLA at
1454, 1709, 1741, 1751 lines. The five selected DLAs
are the DLA at
![]() toward Q0841+129, the DLA toward Q1157+014,
the DLA toward Q1210+17, the DLA toward Q2230+02, and the DLA toward Q2231-00
studied in our first sample of DLAs (see Paper I). Their accessible
Ni II lines, with their corresponding profiles, can be found in
Figs. 4, 8, 10, and 12, and Fig. 6 of Paper I, respectively.
toward Q0841+129, the DLA toward Q1157+014,
the DLA toward Q1210+17, the DLA toward Q2230+02, and the DLA toward Q2231-00
studied in our first sample of DLAs (see Paper I). Their accessible
Ni II lines, with their corresponding profiles, can be found in
Figs. 4, 8, 10, and 12, and Fig. 6 of Paper I, respectively.
Table A.1: Atomic data of the Ni II transitions.
Table A.2:
The new Ni II ![]() 1317 oscillator strength.
1317 oscillator strength.
The new Ni II ![]() 1317 oscillator strength results are
illustrated in Fig. A.1 and summarized in Table A.2.
Instead of showing the derived f-values through the best Voigt profile
fitting solutions obtained for the Ni II lines, we present the results
by plotting the apparent column density
1317 oscillator strength results are
illustrated in Fig. A.1 and summarized in Table A.2.
Instead of showing the derived f-values through the best Voigt profile
fitting solutions obtained for the Ni II lines, we present the results
by plotting the apparent column density
![]() profiles for the
analyzed Ni II lines. The apparent ionic column density for each pixel,
profiles for the
analyzed Ni II lines. The apparent ionic column density for each pixel,
![]() ,
is defined by:
,
is defined by:
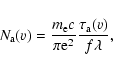
The derived final new Ni II ![]() 1317 oscillator strength is:
1317 oscillator strength is:
![\begin{figure}
\par\includegraphics[width=11.5cm,clip]{3200fig29.ps}\par\vspace*...
...par\vspace*{2mm}
\includegraphics[width=11.5cm,clip]{3200fig31.ps}
\end{figure}](/articles/aa/full/2006/01/aa3200-05/Timg189.gif) |
Figure A.1:
Apparent column density
|