A&A 438, 1149-1161 (2005)
DOI: 10.1051/0004-6361:20042210
Atmospheric and oceanic excitation of the rotation of a three-layer Earth
V. Dehant 1 - O. de Viron1 - M. Greff-Lefftz2
1 - Royal Observatory of Belgium, Avenue Circulaire 3, 1180 Brussels, Belgium
2 -
Institut de Physique du Globe, Paris, France
Received 19 October 2004 / Accepted 24 February 2005
Abstract
In this paper, we evaluate the nutational Earth response to the
excitation exerted by a surface fluid (atmosphere, ocean, and
hydrology) for a simple Earth model, constituted of three
homogeneous layers: a solid deformable inner-core, a liquid outer core,
and an elastic mantle. Our formula, valid in the quasi-diurnal
frequency band, includes two resonances, at the Free Core Nutation
(FCN) and the Free Inner-Core Nutation (FICN). Additionally, we
have evaluated the amplitudes of those wobbles in response to a
random noise excitation. We show that, compared with the FCN
signal, the resonance at the FICN frequency induced by a surface
fluid layer only induces a very small signal in the Earth
rotation, and that, with an excitation comparable to the one
available at the FCN, the FICN would generate a signal at the
Earth surface at the sub-micrometer level.
Key words: Earth - reference systems
The variable Earth rotation is classically separated into three
motions: (i) the motion of the mean Earth rotation axis in space,
i.e. the precession-nutation; (ii) the motion of the mean Earth
around its rotation axis, called polar motion (PM); and (iii) the
variation of the Earth rotation velocity, studied in terms of the
variation of the length-of-day (LOD). The variations of the
length-of-day are mostly excited by the atmosphere (more than 95%
at periods ranging from a few days to several years); the polar
motion is excited by the ocean and the atmosphere at the same
level; and the precession-nutation mainly corresponds to the
response of the Earth to the gravitational action of the Sun, the
Moon, and the other planets.
Nutation is observed using Very Long Baseline Interferometry
(VLBI) with a precision better than a milliarcsecond
(mas) for any observing session, corresponding to the
sub-centimeter level at the Earth's surface. The error on a given
harmonic nutation coefficient is even better.
For most of the nutation waves, the periods are imposed by the
periods of the external forcing, and the internal structure only
affects the magnitude of the response. In addition, the presence
of a fluid core and a solid inner core allows the existence of two
normal modes of which the periods are determined by the physical
characteristics of the Earth. The nutations are excited by the
gravitational forcing from the Sun, the Moon and the other
planets, as well as by the geophysical fluids. The atmosphere and
ocean indeed influence the nutations at those frequencies as well,
but the effects are small relative to the Sun and the Moon
gravitational forcing. As no external wave corresponds exactly to
the periods of the free modes, only the geophysical fluids can
excite the free nutation modes (with a possible exception related
to the excitation by earthquakes). In particular, the atmosphere
and the ocean are thought to be the major excitation sources of
the Free Core Nutation (FCN), see Sasao & Wahr (1981). The Free
Inner-Core Nutation (FICN) free mode is observed by VLBI at the
level of a few tenths of mas (see Herring et al. 1991, 2002). Its amplitude varies with time. In addition the
presence of those free modes amplifies the Earth response for the
waves of frequency close to the resonance frequencies.
The nutation motion is modeled, based on celestial mechanics on the one hand, and on physics of
the Earth interior on the other hand.
The nutation model adopted by the International Astronomical Union and the International Union of Geodesy and
Geophysics (see Mathews et al. 2002) (MHB2000) considers time varying
amplitude of the FCN free mode. The FICN free mode was not
considered. Both modes are believed to be excited by the
atmosphere and the ocean.
The nutational response of the Earth to the gravitational forcing is classically
expressed in terms of a transfer function (TF), so that, for any frequency 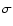 of the
forcing potential, the nutation response is given by
of the
forcing potential, the nutation response is given by
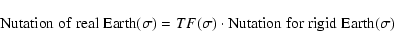 |
(1) |
where the nutations for the rigid Earth are computed directly from
the celestial mechanics. The fluid effects, i.e. the tidal (and
non-tidal) ocean and the atmospheric effects, are added
separately, as they are not proportional to and in phase with the
gravitational potential. In the adopted model, as the atmospheric
and oceanic forcing are not known as precisely as the external
forcing, their effects on the classical nutation waves are fit
(in the atmosphere case) or scaled (ocean case) on the observed
nutation amplitudes.
Up to now, the transfer function representing the response of a
three-layer Earth to this excitation has never been evaluated. The
amplitude of the inner-core mode is thought to be small, as the
inner-core inertia only accounts for one thousandth of the total
Earth inertia. Nevertheless, the observations become increasingly
accurate, and the inner core mode signature might soon reach the
observational level. As this signature depends on the internal
structure of the Earth, its observation would lead to a better
understanding of the Earth's deep interior.
The IAU MHB2000 model of Mathews et al. (2002) is based on the fit of the
parameters of a simple Earth model on the nutation observations.
The associated transfer function includes both FCN and FICN
resonance in the Earth response to gravitational forcing. In
that study, the period and damping of these modes are estimated from the observed VLBI nutations; the
periods are 430 and 1030 days for the FCN and FICN respectively
and their damping factors, represented by the so-called quality
factor, defined as the ratio between the real and the imaginary
part of the frequency divided by two, are 20 000 and 680 respectively. Dehant et al. (2003) have shown that any value within the intervals
given in Table 1 is acceptable as well, considering the
uncertainties on the determinations of nutation amplitudes.
Table 1:
Mean value and interval of values for the periods and
quality factors of the FCN and FICN.
Observation precision gets better with time, due to the
improvements in technology and in observation strategy. When the
modelled nutation (MHB2000 without the free modes) is subtracted
from the observation, the signal associated with the free core
nutation is the major source of residuals. From the analysis of
those residuals, Feissel-Vernier (2003) and Feissel-Vernier et al. (2005) have shown
the presence of some power in the FICN frequency band. This
motivated us to compute theoretically the nutational response of a
three-layer Earth for the normal nutation modes excited by the
noise of the atmosphere and/or the ocean at those frequencies.
In addition to the nutation, the Earth response to the gravitational and
geophysical fluid forcing also includes deformations of its different layers. In our first order approach, the effects of the deformations are assumed to be linear in the potential. The proportionality coefficients between the forcing potential (or surface/internal pressure/load distribution) and the deformation are called Love numbers.
The paper is organized as follows: Sect. 2
describes the model used and the major hypotheses done in our
study, Sect. 3 is devoted to the theoretical computation of the
Earth response to atmospheric/oceanic forcing; Sect. 4 gives the
free mode periods and the transfer functions for the diurnal
wobbles associated with nutations.
Section 5 is devoted to the computation of the Love
numbers (i.e. transfer functions for deformation) involved and the numerical values of the excitation
function, and Sect. 6 provides the Earth response at the FICN
period to random noise atmospheric/oceanic excitation. Conclusions
and discussion are given in Sect. 7.
In our study, we used a simplified Earth model, composed of three
homogeneous ellipsoidal layers, an elastic inner-core, a fluid
core, and an elastic mantle. The three layers are assumed to only
move "rigidly'': small rotations are allowed with respect to the
mean diurnal rotation. Additionally, deformations are allowed,
which are accounted for by using the Love number formalism. The
coupling between the fluid and solid parts is assumed to be only
due to the pressure acting on the ellipsoidal boundaries and to
the gravitational interaction between the three layers.
Nevertheless, considering only non-dissipative forces would lead
to infinite amplitude of the free modes, which is unphysical.
Consequently, we add to the frequency of the mode an imaginary
part which accounts for the dissipation. This dissipation would
come from viscosity in the Earth, topographic coupling at the core
boundaries, and electromagnetic coupling between the core and the
solid layers. The surface fluid layer is assumed to be
"thin layer''. The excitation exerted by the atmosphere and the ocean on
the Earth nutation is assumed to be a white noise in a given
frequency band but some particular frequencies are identified as
relevant for the atmosphere or ocean dynamics. As the angular
momentum approach is used for computing the effect of the fluid
layer, we do not need to assess any properties of the interaction
between the surface fluid layer and the mantle.
The rotation dynamic of a simple Earth model is classically analyzed
using the Liouville equation, which is a particular case of the angular
momentum budget equation. We used a reference frame rotating with the
mantle, with a rotation vector
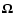 ,
defined by
,
defined by
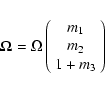 |
(2) |
where 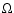 is the Earth mean angular velocity. Note that the rotation perturbation mi are small with respect to 1.
is the Earth mean angular velocity. Note that the rotation perturbation mi are small with respect to 1.
The inertia of the whole Earth,
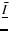 ,
is the one of a biaxial
ellipsoid perturbed by small deformations:
,
is the one of a biaxial
ellipsoid perturbed by small deformations:
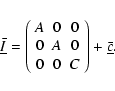 |
(3) |
The incremental part
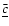 is due to the deformation of each layer in response to the forcing potential, as well as to the change in the atmospheric and oceanic inertia. All the cij are small with respect to the equilibrium moment of inertia.
is due to the deformation of each layer in response to the forcing potential, as well as to the change in the atmospheric and oceanic inertia. All the cij are small with respect to the equilibrium moment of inertia.
The angular momentum of the whole Earth is then given by
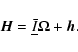 |
(4) |
The addititional angular momentum 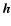 is associated with the
relative angular momentum of the different layers of the whole
Earth: the inner core (
is associated with the
relative angular momentum of the different layers of the whole
Earth: the inner core (
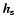 ), the fluid outer core (
), the fluid outer core (
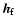 ), and the atmosphere (
), and the atmosphere (
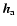 ). Those additional angular
momenta are also small quantities.
). Those additional angular
momenta are also small quantities.
As explained in Sect. 2, we only allow rigid rotation of the core and inner core. Consequently, we have:
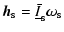 |
|
|
(5) |
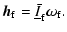 |
|
|
(6) |
The inertia of the inner core and outer core are given by
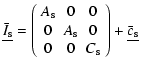 |
|
|
(7) |
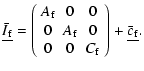 |
|
|
(8) |
With respect to the mantle, the rotation vectors of the inner core and outer core are
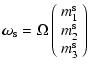 |
|
|
(9) |
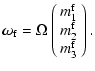 |
|
|
(10) |
As for the solid Earth, the quantities
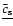 ,
,
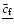 ,
,
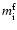 ,
and
,
and
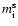 are small.
The time derivative, in the inertial frame, of the angular momentum for the solid Earth
is given by
are small.
The time derivative, in the inertial frame, of the angular momentum for the solid Earth
is given by
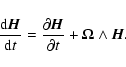 |
(11) |
Using the expression developed here above, it is straight forward to get the equatorial part of the Liouville equations, at the first order in the small quantities, for the whole Earth as:
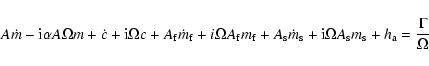 |
(12) |
where
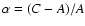 is the dynamic flattening of the
whole Earth and
is the dynamic flattening of the
whole Earth and 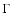 the total torque acting on the Earth.
Similarly, we will note
the total torque acting on the Earth.
Similarly, we will note
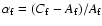 and
and
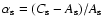 .
.
The x and y components have been complexely added, so that
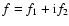 .
In particular, the complex wobble are defined as
.
In particular, the complex wobble are defined as
| |
|
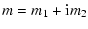 |
(13) |
| |
|
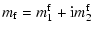 |
(14) |
| |
|
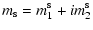 |
(15) |
| |
|
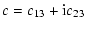 |
(16) |
| |
|
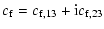 |
(17) |
| |
|
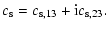 |
(18) |
The rotation vector of the inner core and the outer core in the inertial frame is given by
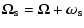 |
|
|
(19) |
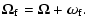 |
|
|
(20) |
In the case of those two layers, there is no differential
angular momentum, as we consider they are rotating rigidely. Consequently,
the angular momentum budget equation, at the first order in the small quantities, are
given by:
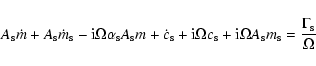 |
(21) |
for the inner core, and
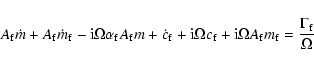 |
(22) |
for the liquid outer core, with
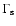 being the
total torque on the inner core,
being the
total torque on the inner core,
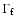 ,
the total torque on
the outer core.
,
the total torque on
the outer core.
Those are the Liouville equations for a three-layer
Earth as done in Dehant et al. (1993) (here after noted D93) and we have
extended these equations in order to account for the effect of a
surface fluid layer. Corrections to these equations, as expressed in
Greff-Lefftz et al. (2000, 2002)
are considered as well. We
have to consider the effects of the external fluid through the
induced changes in three components of the equations: (1) the
relative angular momentum; (2) the changes in the inertia tensor;
and (3) the interaction torques at the core boundaries.
The relative angular momentum of the external fluid, related to
the wind in the atmosphere and to the currents in the ocean, must
be included in the angular momentum budget. This is classically
done using the motion (or wind) angular momentum excitation
function (
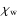 ), as defined in Munk & McDonald (1960). The wind
term of the atmospheric angular momentum is given by
), as defined in Munk & McDonald (1960). The wind
term of the atmospheric angular momentum is given by
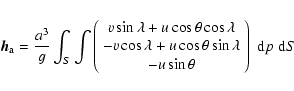 |
(23) |
where 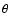 is the colatitude,
is the colatitude, 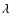 is the longitude, u is the
zonal wind, v, the meridional wind, a is the Earth mean radius, g, the acceleration
of gravity, and
is the longitude, u is the
zonal wind, v, the meridional wind, a is the Earth mean radius, g, the acceleration
of gravity, and 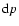 implies that the vertical integration is done in terms of pressure level.
The wind excitation function is defined by its relation to the wind term of the angular momentum:
implies that the vertical integration is done in terms of pressure level.
The wind excitation function is defined by its relation to the wind term of the angular momentum:
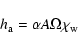 |
(24) |
where 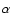 is the Earth dynamical flattening and Ais the Earth equatorial moment of inertia.
is the Earth dynamical flattening and Ais the Earth equatorial moment of inertia.
The inertia increments are computed by integration on the deformed
volume of the
core and of the inner core:
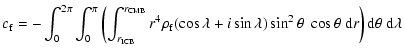 |
|
|
(25) |
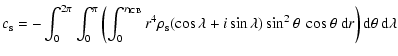 |
|
|
(26) |
where
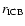 and
and
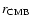 are the radius of the
deformed boundaries of the core (Inner Core Boundary and Core
Mantle Boundary, respectively),
are the radius of the
deformed boundaries of the core (Inner Core Boundary and Core
Mantle Boundary, respectively),
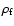 and
and
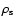 are the
density of the fluid core and solid inner core respectively. Using
the Love number formalism, we can evaluate the topography of the
deformed surface from the forcing potential and pressure
(Greff-Lefftz et al. 2000).
In our notation, the load Love numbers are indicated by a hat
(they account for pressure and loading mass potential effects),
the pressure ones by a bar, and the potential ones left alone.
Note that the Love numbers, by definition, include all the static
indirect effects, as for instance the deformation due to the
change of pressure associated with the external potential acting
on the Earth. They do not, however, include the effects related to
the dynamics, as for instance the deformation associated with the
rotation of the Earth. For this reason, the centrifugal potential
is included in the potential considered, and we have the rotation potential
are the
density of the fluid core and solid inner core respectively. Using
the Love number formalism, we can evaluate the topography of the
deformed surface from the forcing potential and pressure
(Greff-Lefftz et al. 2000).
In our notation, the load Love numbers are indicated by a hat
(they account for pressure and loading mass potential effects),
the pressure ones by a bar, and the potential ones left alone.
Note that the Love numbers, by definition, include all the static
indirect effects, as for instance the deformation due to the
change of pressure associated with the external potential acting
on the Earth. They do not, however, include the effects related to
the dynamics, as for instance the deformation associated with the
rotation of the Earth. For this reason, the centrifugal potential
is included in the potential considered, and we have the rotation potential 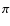 .
If the dynamics effects were included in the Love number, we
would not need to have any other effects considered than the
external forcing (external potential W and external pressure
.
If the dynamics effects were included in the Love number, we
would not need to have any other effects considered than the
external forcing (external potential W and external pressure
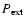 ). We did not consider, in our study, the terms in
product of Love numbers, which are of the second order. It is not
only because those effects are small, considering the numerical
value of the Love number, but also because their numerical values
are not very reliable, as they are most certainly much affected by
the simple approximation done in this study.
). We did not consider, in our study, the terms in
product of Love numbers, which are of the second order. It is not
only because those effects are small, considering the numerical
value of the Love number, but also because their numerical values
are not very reliable, as they are most certainly much affected by
the simple approximation done in this study.
As the surface fluid is included in the "Global Earth'', we have
to take it into account when computing the global increment of
inertia. Additionally, the loading of the surface fluids induces
deformations, which changes the inertia of the global Earth (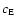 ), the core (
), the core (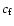 )
and the inner core (
)
and the inner core (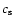 ).
The change of inertia of the whole Earth due to the presence at its surface of a
thin layer of fluid of which the surface pressure is
).
The change of inertia of the whole Earth due to the presence at its surface of a
thin layer of fluid of which the surface pressure is
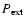 is given by
is given by
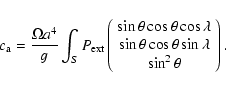 |
(27) |
The mass (or pressure) angular momentum excitation function is defined by its relation
to the inertia change (see Munk & McDonald 1960):
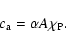 |
(28) |
After some algebra, done for instance in Sasao & Wahr (1981) and Dehant et al. (1993),
it is eventually possible to get the expression of the inertia change as a function
of the rotation variation of the whole planet, of the core, and of the inner core,
of the external forcing and surface pressure, as well as of properties of the Earth model.
where
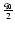 is the ratio between the
centrifugal and gravitational acceleration at the equator,
is the ratio between the
centrifugal and gravitational acceleration at the equator,
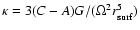 is the fluid Love
number.
is the fluid Love
number.
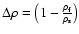 .
The Love
numbers (k0t and h0t) are the classical Love numbers,
expressing the deformation of the Earth in response to a
potential; when they are overlined, they express the deformation
in response to a pressure. The same numbers, when they have a hat,
express the response to a surface load (pressure + gravitational
attraction). The same quantities, for the inner core and the outer
core, are written with s and f instead of t, respectively.
The same numbers, with 2 or 1 instead of 0, have the same
meaning, but the forcing is applied at the Inner Core Boundary
(ICB) or Core Mantle Boundary (CMB) respectively.
.
The Love
numbers (k0t and h0t) are the classical Love numbers,
expressing the deformation of the Earth in response to a
potential; when they are overlined, they express the deformation
in response to a pressure. The same numbers, when they have a hat,
express the response to a surface load (pressure + gravitational
attraction). The same quantities, for the inner core and the outer
core, are written with s and f instead of t, respectively.
The same numbers, with 2 or 1 instead of 0, have the same
meaning, but the forcing is applied at the Inner Core Boundary
(ICB) or Core Mantle Boundary (CMB) respectively.
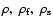 are the (mean) densities of the whole Earth, of
the outer core and of the inner core respectively. As we said in
Sect. 2, we allow a tilt of the inner core with respect to the
mantle. The angle of this tilt is given by
are the (mean) densities of the whole Earth, of
the outer core and of the inner core respectively. As we said in
Sect. 2, we allow a tilt of the inner core with respect to the
mantle. The angle of this tilt is given by
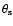 .
This
quantity is linked to the inner core wobble by
.
This
quantity is linked to the inner core wobble by
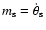 .
For the effect of a load at the ICB on the core inertia, we
need to account for the effect of both the deformation of the ICB
and the CMB. After some algebra, it can be shown that it is
equivalent to have a Love number
.
For the effect of a load at the ICB on the core inertia, we
need to account for the effect of both the deformation of the ICB
and the CMB. After some algebra, it can be shown that it is
equivalent to have a Love number
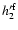 equal to
equal to
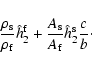 |
(32) |
Additionally,
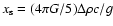 ,
,
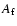 and
and 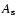 are the equatorial moments of inertia of the core and inner core
respectively, a, b, and c are the radii of the total Earth,
the outer core and the inner core respectively.
are the equatorial moments of inertia of the core and inner core
respectively, a, b, and c are the radii of the total Earth,
the outer core and the inner core respectively.
As the atmosphere is part of the global Earth, there is no need to
add an atmospheric torque in the equations. Note that this is
different from what was done in D93, where the atmospheric
pressure was considered as an external forcing. On the other hand,
the torques at the core boundaries need to be recomputed in this
frame. The angular momentum of the fluid core can be written:
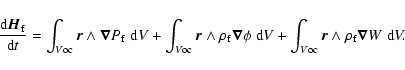 |
(33) |
Where 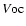 means the volume of the outer core, where
means the volume of the outer core, where
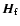 is the core angular momentum,
is the core angular momentum, 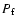 is the
fluid pressure,
is the
fluid pressure, 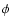 is the gravitational potential associated
with the mass redistribution inside the Earth, and W is the
forcing tidal potential. Without a fully dynamically consistent
model of the core, it is impossible to know the pressure (
is the gravitational potential associated
with the mass redistribution inside the Earth, and W is the
forcing tidal potential. Without a fully dynamically consistent
model of the core, it is impossible to know the pressure (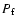 )
inside the core. Consequently, we use the momentum budget equation
to evaluate the pressure: as only conservative forces are acting
on the fluid and as its density is homogeneous, its acceleration
derives from a potential, and we have
)
inside the core. Consequently, we use the momentum budget equation
to evaluate the pressure: as only conservative forces are acting
on the fluid and as its density is homogeneous, its acceleration
derives from a potential, and we have
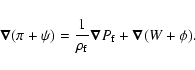 |
(34) |
Where 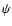 is the centrifugal potential and
is the centrifugal potential and 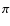 is the potential associated with the acceleration in the
rotating frame. Isolating
is the potential associated with the acceleration in the
rotating frame. Isolating 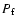 and substituting in the Eq. (33), we get
and substituting in the Eq. (33), we get
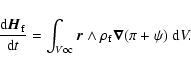 |
(35) |
As 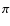 and
and 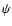 only depend on the rotation of the core and
Earth respectively, they can be written in terms of the unknows of
our problem. Nevertheless, the presence of a surface fluid does
not change the expression of those potentials in terms of the
unknowns. Consequently, the surface fluid will not affect the
expression of the total torque acting on the fluid core, but it
will affect the values of the potential involved in their
expressions.
only depend on the rotation of the core and
Earth respectively, they can be written in terms of the unknows of
our problem. Nevertheless, the presence of a surface fluid does
not change the expression of those potentials in terms of the
unknowns. Consequently, the surface fluid will not affect the
expression of the total torque acting on the fluid core, but it
will affect the values of the potential involved in their
expressions.
The torque on the inner core is computed from the same
Eq. (33), with the density
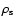 rather than
rather than
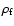 for
the potential parts. When substituting the expression for the
fluid pressure, we get:
for
the potential parts. When substituting the expression for the
fluid pressure, we get:
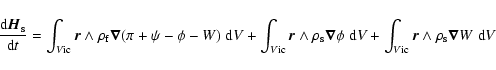 |
(36) |
where 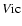 means the volume of the inner core. Regrouping the terms in
means the volume of the inner core. Regrouping the terms in 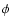 and W, we have
and W, we have
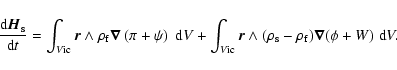 |
(37) |
As in the case of the core, the first term is not affected by the
presence of a surface fluid. On the contrary, the second term
needs to be modified: the mass of the surface fluid has to be included in
the forcing potential, and the resulting deformation has to
be included in the mass redistribution potential. This last effect
is at the second order, and can thus be neglected. After some
(heavy) algebra, we obtain the following final expression for
the torque over the inner core:
Substituting the expression of the increments of inertia and of
the interaction torque, it is straightforward to express the
angular momentum budget equation in terms of the rotation vector
of the mantle, of the core, and of the inner core, and in terms of
the forcing potential (W) and the atmospheric excitation
functions (
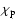 and
and
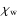 ).
).
Using a Fourier transform to express the budget equations at a
given frequency. The final form of the equation for the global
Earth is:
Similarly, the final form of the equation for the fluid
core is:
And we obtain, for the inner core:
Note that the torques computed here are an improved version of
those computed in Dehant et al. (1993); the pressure is computed on the
deformed surface, which adds a term due to the inner core tilt. We
have also considered the deformation effects induced by
gravitational interaction with a tilted inner-core as proposed by
Greff-Lefftz et al. (2000). Nevertheless, we decided to neglect the terms
involving a coupling between deformations.
This results in a quite
different expression of the pressure effect, and in an additional
term in the global Earth budget equation, with respect to D93.
At the one-layer Earth limit, the global Earth equation is
equivalent to the ones from Barnes et al. (1983). At the two-layer Earth
limit, our expression are equivalent to those of Sasao & Wahr (1981).
In order to evaluate the normal modes of the system formed by
Eqs. (39)-(41) and
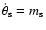 ,
we write the left hand side of those equations in a matrix
form (which multiply the vector
,
we write the left hand side of those equations in a matrix
form (which multiply the vector
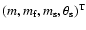 .
.
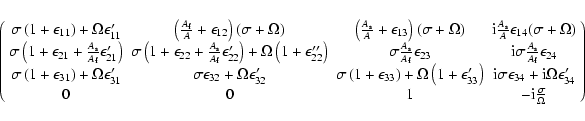 |
(42) |
with:
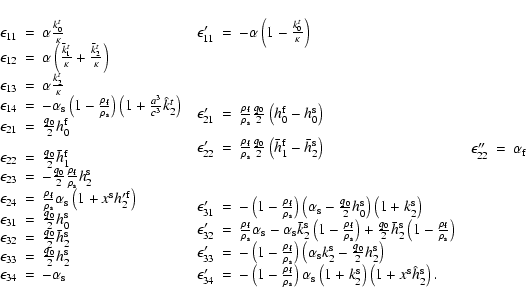 |
(43) |
Solving the homogeneous system, we found the frequency of the free
modes. For computational reasons, it is easier to separate our
problem based on the period: we study separately the low frequency
part of the spectrum (for which 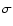 is of the order of
is of the order of
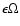 ), and the quasi-diurnal band (for which
), and the quasi-diurnal band (for which
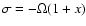 ,
with x of the order of
,
with x of the order of 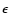 ).
).
The low frequency case is discussed in Dehant et al. (2005), in the case
of Mars. In the nearly diurnal approximation, the matrix is:
Again, as in D93, we find two quasi-diurnal modes:
| |
|
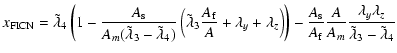 |
(44) |
| |
|
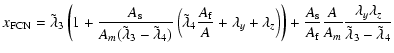 |
(45) |
with
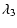 |
= |
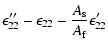 |
(46) |
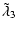 |
= |
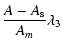 |
(47) |
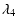 |
= |
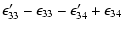 |
(48) |
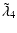 |
= |
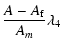 |
(49) |
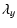 |
= |
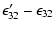 |
(50) |
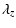 |
= |
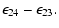 |
(51) |
The dynamic equation system is solved in the quasi-diurnal
frequency band. After some (heavy) algebra, we find a solution
that can be written as:
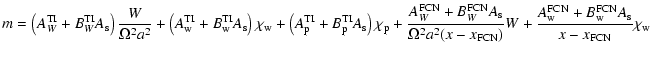 |
|
|
|
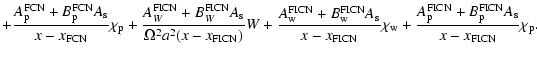 |
|
|
(52) |
For the Earth, 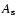 ,
which represents the inertia of the inner
core, is very small, on the order of 10-3 of the inertia of
the mantle. Consequently, the terms in
,
which represents the inertia of the inner
core, is very small, on the order of 10-3 of the inertia of
the mantle. Consequently, the terms in 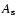 are usually
negligible. Nevertheless, the resonance at the Free Inner Core
Nutation makes it possible to enhance terms in
are usually
negligible. Nevertheless, the resonance at the Free Inner Core
Nutation makes it possible to enhance terms in 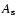 ,
which need
then to be kept in the equation. Thus, the solution that we use in
the following can be expressed as
,
which need
then to be kept in the equation. Thus, the solution that we use in
the following can be expressed as
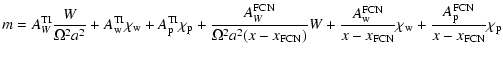 |
|
|
|
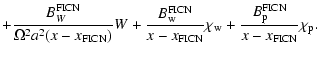 |
|
|
(53) |
The expression for the coefficients in the above equation are
given in the table below. In all the expressions, we limit
ourselves to the lowest possible order in the small quantities,
for each part of the formula, in order to keep all the physics and
the expressions as simple as possible. In particular, this implies
that the non-deformation parts of the atmospheric pressure (
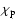 )
terms disappear from the expressions.
)
terms disappear from the expressions.
Table 2:
Analytical expression of the resonance strengths in
Formula (53). The first column indicates the cause and
the normalization of the forcing.
In order to evaluate the Love numbers, we need to solve the
gravito-elasticity equations (as described for instance by Alterman et al. 1959) for a planet composed of three homogeneous
layers, using boundary conditions inside the planet and at the
surface. Those equations are motion equations, stress-strain
relationship, and Poisson equation for the mass redistribution,
and the boundary conditions are continuity of the potential,
stress, and radial displacement at all the boundaries, and free
slip conditions (and thus no tangential stress) at the core
boundaries, under the condition that the solution does not diverge
at the center of the Earth.
In order to express our solution, we used simple analytical
solutions of the radial dependency of our variables which are, as
in Alterman et al. (1959):
- y1, the radial displacement;
- y2, the radial stress;
- y3, the tangential displacement;
- y4, the tangential stress;
- y5, the mass redistribution potential;
- y6, involving y1 and the derivative of y5.
And the analytical solutions used are the following:
At the Earth surface, the boundary conditions are determined from
the forcing. There is no condition on the displacement at the
Earth surface; the tangential stress is zero, and the radial
stress is continuous, i.e. equal to the external pressure. In
addition, there is continuity of the potential and of a
combination of its radial derivative and the radial displacement,
involving the Poisson equation:
where
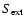 is a load external potential,
is a load external potential,
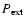 an external pressure,
an external pressure,
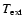 an external
tangential stress, and W an external potential.
an external
tangential stress, and W an external potential.
At the CMB, we have continuity of the radial displacement, but not
of the tangential displacement. In order to allow additional
displacement due to non static response of the Earth, we add
arbitrary constant (K1 and K3) that will be solved for using
the complete system. Additionally, we have continuity of the
radial stress (i.e. pressure) and the tangential stress acting
only on the mantle. We also use the continuity of the potential
and its derivative:
| |
|
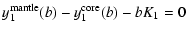 |
(57) |
| |
|
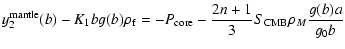 |
(58) |
| |
|
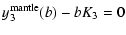 |
(59) |
| |
|
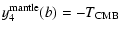 |
(60) |
| |
|
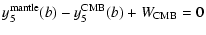 |
(61) |
| |
|
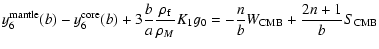 |
(62) |
where
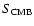 is a loading potential at the CMB,
is a loading potential at the CMB,
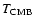 ,
a tangential stress at the CMB, and
,
a tangential stress at the CMB, and
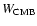 ,
a potential at the CMB.
,
a potential at the CMB.
At the ICB, the continuity conditions are the same as at the CMB
(introducing the arbitrary constants K2 and K4):
| |
|
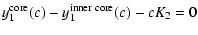 |
(63) |
| |
|
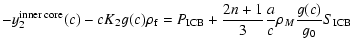 |
(64) |
| |
|
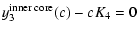 |
(65) |
| |
|
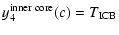 |
(66) |
| |
|
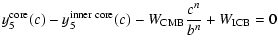 |
(67) |
| |
|
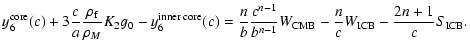 |
(68) |
Using those equations and boundary conditions, we can
solve the system, and we obtain the variables in function of the
forcing and the Earth interior properties.
As those equations are all linear in the potential, we easily get
the expressions and numerical values of the generalized Love
numbers for the three-layer Earth; for instance, the Love number
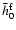 is the numerical coefficient of the
is the numerical coefficient of the
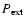 in
the expression of the CMB radial deformation (
in
the expression of the CMB radial deformation (
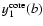 ). The Love number h0t is, by definition, the value
of y1 at the surface, when the forcing potential is set to
1/g0. Similarly, the other Love numbers h are estimated from
the values of y1 at the different interfaces, for forcings
placed at the relevant interfaces. The values of k are computed
as the values of y5, when the forcing potential is set to 1.
). The Love number h0t is, by definition, the value
of y1 at the surface, when the forcing potential is set to
1/g0. Similarly, the other Love numbers h are estimated from
the values of y1 at the different interfaces, for forcings
placed at the relevant interfaces. The values of k are computed
as the values of y5, when the forcing potential is set to 1.
Table 4 gives the numerical values of the Earth model properties
used in our computation and Table 5 gives the numerical
values of the Love numbers obtained in our study. Those values are
derived as mean values from PREM (Dziewonski & Anderson 1981).
The solutions for the wobble m as a function of the frequency and the forcing is:
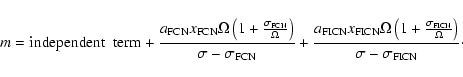 |
(69) |
The polar motion is given by, see for instance Gross (1992),
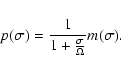 |
(70) |
We are looking for an expression of the Power Spectral Density
(PSD) of the excited polar motion as a function of the PSD of the
atmospheric (or oceanic) excitation. The PSD on the arbitrarily
small interval centered at the resonance frequency (
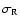 )
is
computed (Lambert 2003) as
)
is
computed (Lambert 2003) as
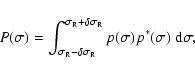 |
(71) |
where
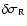 is the half-size of the window,
the * is for complex conjugate, and
is the half-size of the window,
the * is for complex conjugate, and 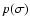 is the polar
motion excited by the atmosphere at frequency
is the polar
motion excited by the atmosphere at frequency 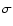 .
It is
given by
.
It is
given by
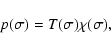 |
(72) |
with 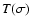 ,
the transfer function as given by Eqs. (69) and (70), and
,
the transfer function as given by Eqs. (69) and (70), and
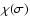 is the
excitation function at frequency
is the
excitation function at frequency 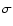 .
.
According to our white noise hypothesis, we have
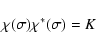 |
(73) |
K is independent of the frequency. At frequencies
close to the resonance frequency
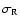 ,
the transfer function
is dominated by the term in
,
the transfer function
is dominated by the term in
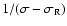 .
Consequently,
in our first order approach, we can limit our-self to that term,
and we get, considering Eq. (73),
.
Consequently,
in our first order approach, we can limit our-self to that term,
and we get, considering Eq. (73),
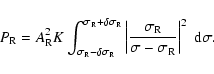 |
(74) |
Note that, in the nutation case, the frequencies has to be taken
in the celestial frame, whereas for the polar motion, they have to
be taken in the Earth frame. The resonance frequency is complex
and can be written as
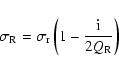 |
(75) |
where 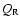 is the quality factor of the resonance and
is the quality factor of the resonance and
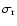 is the real part of the resonance frequency.
is the real part of the resonance frequency.
From this expression, it is straightforward to get
We then choose the
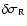 so that 99% of the energy is
included in the interval. Imposing the condition gives, for any
resonance frequency,
so that 99% of the energy is
included in the interval. Imposing the condition gives, for any
resonance frequency,
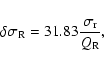 |
(77) |
which leads to
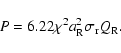 |
(78) |
Consequently, if we assume that the forcing PSD is of the same
order at the FCN and FICN periods, we can estimate the ratio
between the signal at the two resonances:
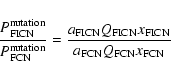 |
(79) |
where
 indicates that the PSD is for
the nutation and not for the associated wobble or the associated polar motion (using
Eq. (70) expressed in space).
indicates that the PSD is for
the nutation and not for the associated wobble or the associated polar motion (using
Eq. (70) expressed in space).
Using the transfer function of Sect. 4 and the Love numbers of
Sect. 5, we can evaluate this ratio for a wind (
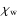 )
and a
pressure (
)
and a
pressure (
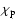 )
excitation. First, the ratio between the
resonance amplitude is given by:
)
excitation. First, the ratio between the
resonance amplitude is given by:
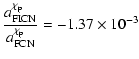 |
|
|
(80) |
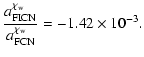 |
|
|
(81) |
Those numbers are at the same order as what would be
obtained, in the case of a forcing by an external potential, from
the numbers of Table 3b in Mathews et al. (2002).
Using our expression for the resonance frequency, we obtain a
ratio between
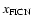 and
and
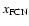 of 1.07. Note that, by
using the adopted values for the periods of these mode (see
Mathews et al. 2002), this ratio is slightly larger than 2. Our
simplified model does not consider any dissipation, and thus can
not provide a ratio between the quality factor. Consequently, we
use the ones of Mathews et al. (2002), whose ratio is 0.034.
of 1.07. Note that, by
using the adopted values for the periods of these mode (see
Mathews et al. 2002), this ratio is slightly larger than 2. Our
simplified model does not consider any dissipation, and thus can
not provide a ratio between the quality factor. Consequently, we
use the ones of Mathews et al. (2002), whose ratio is 0.034.
The ratio between the atmospherically excited FICN and FCN is thus
at the level of
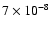 .
Using this ratio, if we consider
the same excitation of the FICN as of the FCN, we would get an
amplitude of
.
Using this ratio, if we consider
the same excitation of the FICN as of the FCN, we would get an
amplitude of
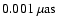 ,
if excited by white noise only. Note
that the period of the FICN, as expected by Mathews et al. (2002), is
close to the ENSO band, which might create a non white noise
excitation around the FICN period (2.7 years). In Yseboodt (2002),
it was shown that the S1 excitation might have been modulated
by the ENSO cycle. This might be the only chance to see the
atmospherically induced free mode of the FICN, as the level of the
observation precision is 0.01 mas.
,
if excited by white noise only. Note
that the period of the FICN, as expected by Mathews et al. (2002), is
close to the ENSO band, which might create a non white noise
excitation around the FICN period (2.7 years). In Yseboodt (2002),
it was shown that the S1 excitation might have been modulated
by the ENSO cycle. This might be the only chance to see the
atmospherically induced free mode of the FICN, as the level of the
observation precision is 0.01 mas.
Table 3:
Analytical expression for Alterman et al. (1959) solution of
the gravito-elastic deformation equations, generalized for a
three-layer Earth.
Table 4:
Numerical value of the Earth model
properties, from PREM.
Table 5:
Numerical value of the Love numbers.
In this paper, we investigate the response of a three-layered
Earth to an atmospheric or oceanic forcing. In particular, we were
interested to evaluate the level at which the FICN could be
excited by an atmospheric random signal. This study was motivated
by detection of a prograde signal in the 1990-95 VLBI observations
at a period consistent with a possible FICN signal, at the level
of 20 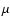 as. As the effect of the external gravitational forcing
was already removed in the residuals, only an atmospheric or
oceanic source was possible, if the cause was to be geophysical.
In the light of the above results, it is extremely unlikely that
the atmosphere might excite such a "large'' signal. Consequently,
we have to find the explanation of those residuals either in the
nutation model or in the observation. In a companion paper,
Feissel-Vernier et al. (2005) investigate the mapping of slight instabilities
in the VLBI celestial reference frame onto the nutation
estimation. They find that the intense activity taking place in
the extragalactic radio sources gives rise to a jitter in their
observed directions at the level of tens of
as. As the effect of the external gravitational forcing
was already removed in the residuals, only an atmospheric or
oceanic source was possible, if the cause was to be geophysical.
In the light of the above results, it is extremely unlikely that
the atmosphere might excite such a "large'' signal. Consequently,
we have to find the explanation of those residuals either in the
nutation model or in the observation. In a companion paper,
Feissel-Vernier et al. (2005) investigate the mapping of slight instabilities
in the VLBI celestial reference frame onto the nutation
estimation. They find that the intense activity taking place in
the extragalactic radio sources gives rise to a jitter in their
observed directions at the level of tens of 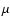 as. By chance it
happened that these apparent motions could mimic a 20
as. By chance it
happened that these apparent motions could mimic a 20 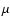 as
880-day prograde periodic component in the
celestial pole motion over the 1990-95 time span. This
seems to be a much more convincing explanation for the observed
residuals.
as
880-day prograde periodic component in the
celestial pole motion over the 1990-95 time span. This
seems to be a much more convincing explanation for the observed
residuals.
Nevertheless, we can not rule out the (remote) possibility that,
in the geophysical fluids (atmosphere, ocean, core), there would
be a free mode at a frequency corresponding exactly to that
frequency, which would excite the FICN to an observable level. At
present, the quality of the diurnal cycle in the Global
Circulation Models of those fluids is much too low to really
investigate this option. We used a simplified Earth model, which
might create some imprecision in our results. Nevertheless,
considering the order of magnitude between the observable level
and the possible FICN excitation, it is not likely that it would
change our conclusion.
Acknowledgements
The work of OdV was financially supported by the Belgian Service
Public fédéral de Programmation Politique scientifique. The
authors thank C. Bizouard and S. Lambert for useful discussions.
- Alterman, Z.,
Jarosch, H., & Pekeris, C. L. 1959, Proc. R. Soc. London A,
252, 80 [NASA ADS] (In the text)
- Barnes, R. T. H.,
Hide, R., White, A. A., & Wilson, C. A. 1983, Proc. R. Soc.
London A, 387, 31 [NASA ADS] (In the text)
- Brzezinski, A. 1994,
Manuscripta Geodaetica, 19, 157
- Brzezinski, A.,
Bizouard, C., & Petrov, S. 2002, Surveys Geophys., 23, 33 [CrossRef]
- Dehant, V., Hinderer,
J., Legros, H., & Lefftz, M. 1993, Phys. Earth Planet. Inter.,
76, 259 [NASA ADS] [CrossRef] (In the text)
- Dehant, V.,
Feissel-Vernier, M., de Viron, O., et al. 2003, J. Geophys. Res.,
108(B5), 2275
(In the text)
- Dehant, V., de Viron,
O., Van Hoolst, T., & Karatekin, O. 2005, in preparation
(In the text)
- Dziewonski, A. D., &
Anderson, D. L. 1981, Phys. Earth Planet. Inter., 25, 297 [NASA ADS] [CrossRef] (In the text)
- Feissel-Vernier,
M. 2003, A&A, 403, 105 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Feissel-Vernier,
M., Ma, C., Gontier, A.-M., & Barache, C. 2005, A&A, 438,
1141 [EDP Sciences] [CrossRef] (In the text)
- Greff-Lefftz, M.,
Legros, H., & Dehant, V. 2000, Phys. Earth planet. Inter., 122,
187 [NASA ADS] [CrossRef] (In the text)
- Greff-Lefftz, M.,
Dehant, V., & Legros, H. 2002, Phys. Earth planet. Inter., 129,
31 [NASA ADS] [CrossRef]
- Gross, R. S.
1992, Geophys. J. Int., 109, 162 [NASA ADS] (In the text)
- Herring, T. A.,
Buffett, B. A., Mathews, P. M., & Shapiro, I. I. 1991, J.
Geophys. Res., 96(B5), 8259
(In the text)
- Herring, T. A.,
Mathews, P. M., & Buffett, B. A. 2002, J. Geophys. Res.,
107(B4)
- Lambert, S. 2003,
Ph.D. Thesis, Observatoire de Paris, France [in French]
(In the text)
- Mathews, P. M.,
Herring, T. A., & Buffett, B. A. 2002, J. Geophys. Res.,
107(B10)
(In the text)
- Munk, W. H.,
& McDonald, G. F. 1960, The Rotation of the Earth, a
Geophysical discussion (Cambridge University Press), 323
(In the text)
- Sasao, T., &
Wahr, J. M. 1981, Geophys. J. R. Astron. Soc., 64, 729 [NASA ADS] (In the text)
- Yseboodt, M., de
Viron, O., Chin, T. M. , & Dehant., V. 2002, J. Geophys. Res.,
107(B2)
(In the text)
Copyright ESO 2005
![]() of the
forcing potential, the nutation response is given by
of the
forcing potential, the nutation response is given by
![]() ,
defined by
,
defined by
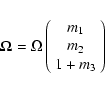
![]() ,
is the one of a biaxial
ellipsoid perturbed by small deformations:
,
is the one of a biaxial
ellipsoid perturbed by small deformations:
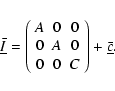
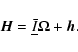
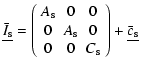
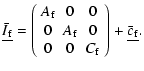
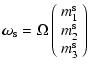
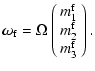
![]() ,
,
![]() ,
,
![]() ,
and
,
and
![]() are small.
The time derivative, in the inertial frame, of the angular momentum for the solid Earth
is given by
are small.
The time derivative, in the inertial frame, of the angular momentum for the solid Earth
is given by
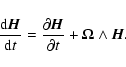
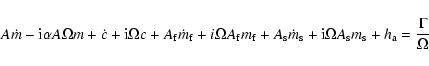
![]() .
In particular, the complex wobble are defined as
.
In particular, the complex wobble are defined as
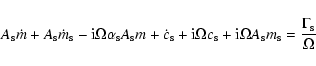
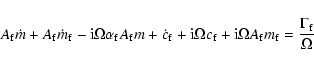
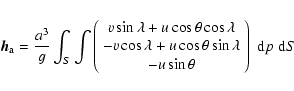
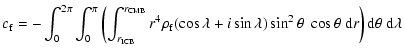
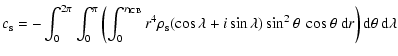
![]() ), the core (
), the core (![]() )
and the inner core (
)
and the inner core (![]() ).
The change of inertia of the whole Earth due to the presence at its surface of a
thin layer of fluid of which the surface pressure is
).
The change of inertia of the whole Earth due to the presence at its surface of a
thin layer of fluid of which the surface pressure is
![]() is given by
is given by
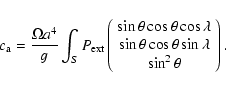
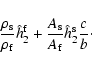
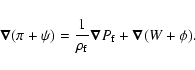
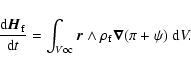
![]() rather than
rather than
![]() for
the potential parts. When substituting the expression for the
fluid pressure, we get:
for
the potential parts. When substituting the expression for the
fluid pressure, we get:
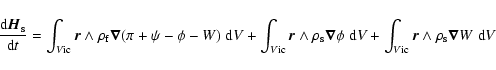
![]() means the volume of the inner core. Regrouping the terms in
means the volume of the inner core. Regrouping the terms in ![]() and W, we have
and W, we have
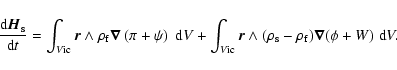
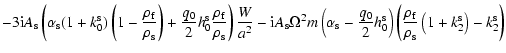
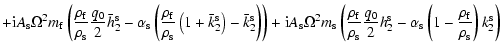
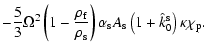
![]() ,
we write the left hand side of those equations in a matrix
form (which multiply the vector
,
we write the left hand side of those equations in a matrix
form (which multiply the vector
![]() .
.
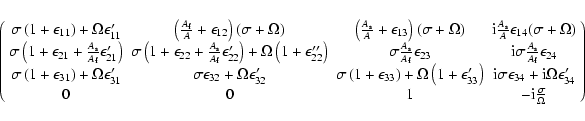
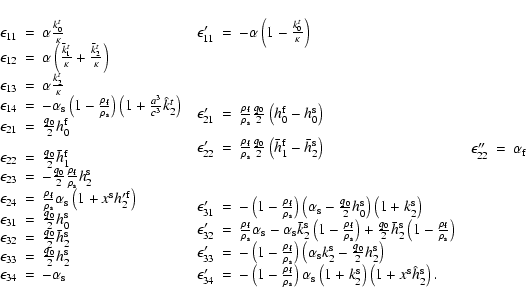
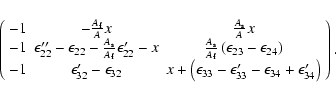
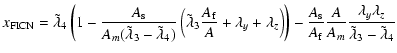
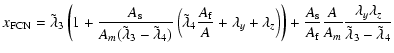
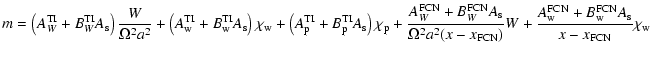
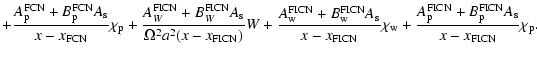
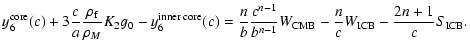
![]() is the numerical coefficient of the
is the numerical coefficient of the
![]() in
the expression of the CMB radial deformation (
in
the expression of the CMB radial deformation (
![]() ). The Love number h0t is, by definition, the value
of y1 at the surface, when the forcing potential is set to
1/g0. Similarly, the other Love numbers h are estimated from
the values of y1 at the different interfaces, for forcings
placed at the relevant interfaces. The values of k are computed
as the values of y5, when the forcing potential is set to 1.
). The Love number h0t is, by definition, the value
of y1 at the surface, when the forcing potential is set to
1/g0. Similarly, the other Love numbers h are estimated from
the values of y1 at the different interfaces, for forcings
placed at the relevant interfaces. The values of k are computed
as the values of y5, when the forcing potential is set to 1.
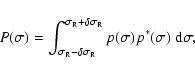
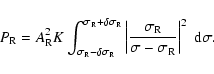
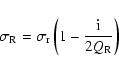
![$\displaystyle a^2_{\rm R}K \frac{-\sigma_{\rm r}}{2Q_{\rm R}} \left(1+4Q_{\rm R...
...t]
_{\sigma_{\rm R}-\delta\sigma_{\rm R}}^{\sigma_{\rm R}+\delta\sigma_{\rm R}}$](/articles/aa/full/2005/30/aa2210-04/img187.gif)
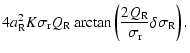
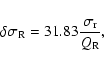
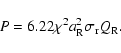
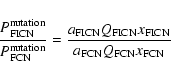
![]() )
and a
pressure (
)
and a
pressure (
![]() )
excitation. First, the ratio between the
resonance amplitude is given by:
)
excitation. First, the ratio between the
resonance amplitude is given by:
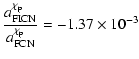
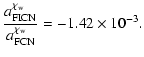
![]() and
and
![]() of 1.07. Note that, by
using the adopted values for the periods of these mode (see
Mathews et al. 2002), this ratio is slightly larger than 2. Our
simplified model does not consider any dissipation, and thus can
not provide a ratio between the quality factor. Consequently, we
use the ones of Mathews et al. (2002), whose ratio is 0.034.
of 1.07. Note that, by
using the adopted values for the periods of these mode (see
Mathews et al. 2002), this ratio is slightly larger than 2. Our
simplified model does not consider any dissipation, and thus can
not provide a ratio between the quality factor. Consequently, we
use the ones of Mathews et al. (2002), whose ratio is 0.034.
![]() .
Using this ratio, if we consider
the same excitation of the FICN as of the FCN, we would get an
amplitude of
.
Using this ratio, if we consider
the same excitation of the FICN as of the FCN, we would get an
amplitude of
![]() ,
if excited by white noise only. Note
that the period of the FICN, as expected by Mathews et al. (2002), is
close to the ENSO band, which might create a non white noise
excitation around the FICN period (2.7 years). In Yseboodt (2002),
it was shown that the S1 excitation might have been modulated
by the ENSO cycle. This might be the only chance to see the
atmospherically induced free mode of the FICN, as the level of the
observation precision is 0.01 mas.
,
if excited by white noise only. Note
that the period of the FICN, as expected by Mathews et al. (2002), is
close to the ENSO band, which might create a non white noise
excitation around the FICN period (2.7 years). In Yseboodt (2002),
it was shown that the S1 excitation might have been modulated
by the ENSO cycle. This might be the only chance to see the
atmospherically induced free mode of the FICN, as the level of the
observation precision is 0.01 mas.