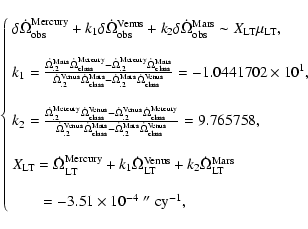A&A 431, 385-389 (2005)
DOI: 10.1051/0004-6361:20041646
Is it possible to measure the Lense-Thirring effect on the
orbits of the planets in the gravitational field of the Sun?
L. Iorio
Dipartimento di Fisica dell'Università di Bari, via Amendola 173, 70126 Bari, Italy
Received 12 July 2004 / Accepted 5 October 2004
Abstract
In this paper we explore a novel approach to try to
measure the post-Newtonian 1/c2 Lense-Thirring secular effect
induced by the gravitomagnetic field of the Sun on planetary
orbital motion. Due to the relative smallness of the solar
angular momentum J and the large values of the planetary
semimajor axes a, the gravitomagnetic precessions, which affect
the nodes 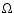 and the perihelia
and the perihelia 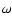 and are proportional
to J/a3, are of the order of 10-3 arcsec per century
only for, e.g., Mercury. This value lies just at the edge of the
present-day observational sensitivity in reconstructing the
planetary orbits, although the future mission BepiColombo should
allow it to be increased. The major problems come from the main
sources of systematic errors. They are the aliasing classical
precessions induced by the multipolar expansion of the Sun's
gravitational potential and the classical secular N-body
precessions which are of the same order of magnitude or much
larger than the Lense-Thirring precessions of interest. This
definitely rules out the possibility of analyzing only one orbital
element of, e.g., Mercury. In order to circumvent these problems,
we propose a suitable linear combination of the orbital residuals
of the nodes of Mercury, Venus and Mars which is, by construction,
independent of such classical secular precessions. A 1-sigma
reasonable estimate of the obtainable accuracy yields a 36
and are proportional
to J/a3, are of the order of 10-3 arcsec per century
only for, e.g., Mercury. This value lies just at the edge of the
present-day observational sensitivity in reconstructing the
planetary orbits, although the future mission BepiColombo should
allow it to be increased. The major problems come from the main
sources of systematic errors. They are the aliasing classical
precessions induced by the multipolar expansion of the Sun's
gravitational potential and the classical secular N-body
precessions which are of the same order of magnitude or much
larger than the Lense-Thirring precessions of interest. This
definitely rules out the possibility of analyzing only one orbital
element of, e.g., Mercury. In order to circumvent these problems,
we propose a suitable linear combination of the orbital residuals
of the nodes of Mercury, Venus and Mars which is, by construction,
independent of such classical secular precessions. A 1-sigma
reasonable estimate of the obtainable accuracy yields a 36 error. Since the major role in the proposed combination is played
by Mercury's node, it could happen that new, more accurate
ephemerides available in the future thanks to the BepiColombo
mission will offer an opportunity to improve the present
unfavorable situation.
error. Since the major role in the proposed combination is played
by Mercury's node, it could happen that new, more accurate
ephemerides available in the future thanks to the BepiColombo
mission will offer an opportunity to improve the present
unfavorable situation.
Key words: gravitation - celestial mechanics - solar system: general
According to the linearized weak-field and slow-motion
approximation of the General Theory of Relativity (GTR), valid
throughout the Solar System, the secular gravitomagnetic
Lense-Thirring precessions on the longitude of the ascending node
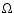 and the argument of pericentre
and the argument of pericentre 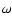 of the orbit of a
test particle freely orbiting around a central mass M with
proper angular momentum J are (Lense & Thirring
1918)
of the orbit of a
test particle freely orbiting around a central mass M with
proper angular momentum J are (Lense & Thirring
1918)
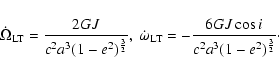 |
(1) |
In Eq. (1) Gis the Newtonian constant of gravitation, c is the speed of
light in vacuum, a,e and i are the semimajor axis, the
eccentricity and the inclination, respectively, of the orbit to
the reference  plane which coincides with the equatorial
plane of the central mass. Its spin J is assumed to be directed
along the z axis.
plane which coincides with the equatorial
plane of the central mass. Its spin J is assumed to be directed
along the z axis.
Up to now, there is no direct observational verification possible
of this prediction of GTR which can be considered reliable and
undisputable.
Indeed, the only attempts performed to detect the Lense-Thirring
precessions of Eq. (1) in the Solar System arena are due to I.
Ciufolini and coworkers (Ciufolini et al. 1998). They analyzed the
orbital data of the existing laser-ranged geodetic LAGEOS and
LAGEOS II satellites in the gravitational field of the Earth over
an observational time span of a few years. In particular, a linear
combination of the residuals of the nodes
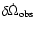 of LAGEOS and LAGEOS II and the perigee
of LAGEOS and LAGEOS II and the perigee
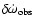 of LAGEOS II (Ciufolini 1996) was
adopted. The residuals were suitably built up in order to entirely
absorb the Lense-Thirring effect in them by setting it purposely
equal to zero in the force models of the equations of motion in
the satellite data reduction software. The claimed total accuracy
would be of the order of 20-30
of LAGEOS II (Ciufolini 1996) was
adopted. The residuals were suitably built up in order to entirely
absorb the Lense-Thirring effect in them by setting it purposely
equal to zero in the force models of the equations of motion in
the satellite data reduction software. The claimed total accuracy
would be of the order of 20-30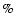 ,
but, according to other
scientists, such estimates would be largely optimistic (Ries et al. 2003).
,
but, according to other
scientists, such estimates would be largely optimistic (Ries et al. 2003).
In April 2004 the extraordinarily sophisticated GP-B mission
(Everitt et al. 2001) was launched. Its goal is to measure another
gravitomagnetic effect in the terrestrial gravitational field,
i.e. the precession of the spins of four superconductor gyroscopes
(Schiff 1960) carried onboard. The claimed accuracy is of the
order of 1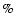 or better. The experiment should last one year.
or better. The experiment should last one year.
Almost twenty years ago it was proposed to launch a third
LAGEOS-like satellite - the LAGEOS III/LARES - and to analyze the
time series of the sum of the residuals of the nodes of LAGEOS and
LARES (Ciufolini 1986) or some other combinations of residuals of
the nodes and the perigees of LARES and both the existing LAGEOS
satellites (Iorio et al. 2002). The obtainable accuracy would
probably be of the order of 1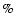 .
Mainly funding problems have
prevented, up to now, implementation of such a relatively easy and
cheap mission. Recently, the possibility of measuring the
Lense-Thirring precessions of Eq. (1) by means of the
relativity-dedicated OPTIS spacecraft, which could be launched in
the same orbital configuration of LARES, has been considered
(Iorio et al. 2004).
.
Mainly funding problems have
prevented, up to now, implementation of such a relatively easy and
cheap mission. Recently, the possibility of measuring the
Lense-Thirring precessions of Eq. (1) by means of the
relativity-dedicated OPTIS spacecraft, which could be launched in
the same orbital configuration of LARES, has been considered
(Iorio et al. 2004).
The recently-proposed LATOR (Turyshev et al. 2004) and ASTROD (Ni
et al. 2004) missions would be sensitive to the gravitomagnetic
part of the bending of light rays in the gravitational field of
the Sun.
According to Nordtvedt (2003), the multidecade analysis of the
Moon's motion with the Lunar Laser Ranging (LLR) technique
strongly supports the existence of the gravitomagnetic
force![[*]](/icons/foot_motif.gif) as predicted by GTR, although in an indirect way.
as predicted by GTR, although in an indirect way.
To measure explicitly the Lense-Thirring precessions of Eq. (1)
from the analysis of the orbital motion of test masses in the
gravitational field of a real rotating astronomical mass like the
Earth or the Sun, the main problems come from the aliasing
effects induced by a host of classical orbital perturbations of
gravitational origin![[*]](/icons/foot_motif.gif) which unavoidably affect the motion of the probes
along with GTR. In particular, the even zonal harmonics
which unavoidably affect the motion of the probes
along with GTR. In particular, the even zonal harmonics 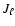 of the multipolar expansion of the gravitational potential of the
central mass induce secular classical precessions which, in many
cases, are larger than the gravitomagnetic ones of interest.
As we will see, the approach proposed by Ciufolini (1996) and
Iorio (Iorio 2002; Iorio & Morea 2004) in the performed or
proposed tests with LAGEOS and LAGEOS II consists of suitably
designing linear combinations
of the multipolar expansion of the gravitational potential of the
central mass induce secular classical precessions which, in many
cases, are larger than the gravitomagnetic ones of interest.
As we will see, the approach proposed by Ciufolini (1996) and
Iorio (Iorio 2002; Iorio & Morea 2004) in the performed or
proposed tests with LAGEOS and LAGEOS II consists of suitably
designing linear combinations
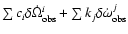 that are able to
reduce the impact of the even zonal harmonics of the gravitational
field of the central mass by cancelling out N-1 selected even
zonal harmonics
that are able to
reduce the impact of the even zonal harmonics of the gravitational
field of the central mass by cancelling out N-1 selected even
zonal harmonics![[*]](/icons/foot_motif.gif) where N is the number of orbital elements
involved.
where N is the number of orbital elements
involved.
In this paper we investigate the possibility of extending the
Ciufolini-Iorio approach in order to try to measure the
Lense-Thirring effect of Eq. (1) in the gravitational field of
the Sun by suitably combining the data from interplanetary ranging
to the inner planets of the Solar System. The relevant parameters
are listed in Table 1.
What is the current approach in testing post-Newtonian gravity
from planetary data analysis followed by, e.g., the Jet Propulsion
Laboratory (JPL)? In the interplay between the real data and the
equations of motion, which include also the post-Newtonian
accelerations expressed in terms of the various PPN parameters
(Will 1993), a set of astrodynamical parameters, among which are
also 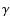 and
and 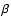 ,
are simultaneously and
straightforwardly fitted and adjusted and a correlation matrix is
also determined. This means that the post-Newtonian equations of
motion are globally tested as a whole in terms of, among other
parameters,
,
are simultaneously and
straightforwardly fitted and adjusted and a correlation matrix is
also determined. This means that the post-Newtonian equations of
motion are globally tested as a whole in terms of, among other
parameters, 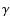 and
and 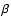 ;
no attention is paid to any
particular feature of the post-Newtonian acceleration. This is
similar to the LLR approach outlined before. On the contrary, our
aim is isolate one particular piece of the post-Newtonian
equations of motion, i.e. the gravitomagnetic acceleration.
;
no attention is paid to any
particular feature of the post-Newtonian acceleration. This is
similar to the LLR approach outlined before. On the contrary, our
aim is isolate one particular piece of the post-Newtonian
equations of motion, i.e. the gravitomagnetic acceleration.
Table 1:
Relevant astronomical and astrophysical parameters used
in the text. The value for the Sun's angular momentum J has been
obtained from (Pijpers 2003). The planetary data can be retrieved
at http://nssdc.gsfc.nasa.gov/planetary/factsheet/.
Table 2:
Gravitomagnetic and classical nodal precession
coefficients, in '' cy-1. The coefficients
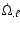 are
are
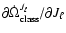 and
refer to the classical precessions induced by the oblateness of
the central mass. The numerical values of Table 1
have been used in Eqs. (1) and (5) (see below).
and
refer to the classical precessions induced by the oblateness of
the central mass. The numerical values of Table 1
have been used in Eqs. (1) and (5) (see below).
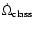 are the nominal centennial rates released
at http://ssd.jpl.nasa.gov/elem_planets.html. They
mainly include the N-body secular precessions.
are the nominal centennial rates released
at http://ssd.jpl.nasa.gov/elem_planets.html. They
mainly include the N-body secular precessions.
In the case of the Sun and the planets, the Lense-Thirring effect
is quite small: indeed, for, e.g., the node it is 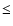 10-3 arcsec per century ('' cy-1), as it can be inferred from Tables 1 and 2. The angular momentum of the
Sun is relatively small and the Lense-Thirring precessions fall
off with the inverse of the third power of the planet's semimajor
axis. If we want to consider the detection of Eq. (1) as a
genuine test of GTR, it is necessary that the Sun's angular
momentum J is known with high accuracy from measurements
independent of GTR itself. This is the case: indeed, the
helioseismic data from the Global Oscillations Network Group
(GONG) and also from the Solar and Heliospheric Observatory (SoHO)
satellite yield measurements of J which are accurate to a few
percent (Pijpers 2003).
10-3 arcsec per century ('' cy-1), as it can be inferred from Tables 1 and 2. The angular momentum of the
Sun is relatively small and the Lense-Thirring precessions fall
off with the inverse of the third power of the planet's semimajor
axis. If we want to consider the detection of Eq. (1) as a
genuine test of GTR, it is necessary that the Sun's angular
momentum J is known with high accuracy from measurements
independent of GTR itself. This is the case: indeed, the
helioseismic data from the Global Oscillations Network Group
(GONG) and also from the Solar and Heliospheric Observatory (SoHO)
satellite yield measurements of J which are accurate to a few
percent (Pijpers 2003).
2.1 Sensitivity analysis
According to the results of Table 3 (E.M. Standish 2004,
private communication), it should be possible to extract the
gravitomagnetic signature from a multi-year analysis of the
residuals of the planetary nodal evolution![[*]](/icons/foot_motif.gif) . Standish averaged, among other things, the nodal
evolution of some planets over two centuries by using the DE405
ephemerides (Standish 1998) with and without post-Newtonian
accelerations. Standish also included in the force models the
solar oblateness with
. Standish averaged, among other things, the nodal
evolution of some planets over two centuries by using the DE405
ephemerides (Standish 1998) with and without post-Newtonian
accelerations. Standish also included in the force models the
solar oblateness with
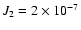 ,
so that the
so-obtained numerical residuals accounted for the post-Newtonian
effects only; the uncertainty in the determined shift for, e.g.,
Mercury, was
,
so that the
so-obtained numerical residuals accounted for the post-Newtonian
effects only; the uncertainty in the determined shift for, e.g.,
Mercury, was
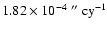 .
The quoted uncertainty of Table 3 does not come from direct observational errors. The
uncertainties depend on the fact that in the force models used in
the numerical propagation many astrodynamical parameters occur
(masses of planets, asteroids, etc.); their numerical values come
from multiparameter fits of real data and, consequently, are
affected by observational errors. Such numerical tests cannot
determine whether GTR is correct or not; they just give an idea of
what the obtainable accuracy set up by our knowledge of the Solar
System would be if the Einstein theory of gravitation is true.
.
The quoted uncertainty of Table 3 does not come from direct observational errors. The
uncertainties depend on the fact that in the force models used in
the numerical propagation many astrodynamical parameters occur
(masses of planets, asteroids, etc.); their numerical values come
from multiparameter fits of real data and, consequently, are
affected by observational errors. Such numerical tests cannot
determine whether GTR is correct or not; they just give an idea of
what the obtainable accuracy set up by our knowledge of the Solar
System would be if the Einstein theory of gravitation is true.
Table 3:
Errors in the numerical propagation of the planetary
nodal rates averaged over 200 years, in '' cy-1 (E.M. Standish 2004,
private communication).
Our knowledge of the orbital motion of Mercury will improve thanks
to the future missions Messenger (see http://messenger.jhuapl.edu/ and http://discovery.nasa.gov/messenger.html), which was launched
in the summer 2004 and whose encounter with Mercury is scheduled
for 2011, and, especially![[*]](/icons/foot_motif.gif) , BepiColombo (see
http://sci.esa.int/science-e/www/area/index.cfm?fareaid=30), which
is scheduled for
2010-2012. A complete error analysis for the
range and range-rate measurements can be found in Iess & Boscagli
(2001). According to them, a two orders of magnitude improvement
in the Earth-Mercury range should be possible. According to a more
conservative evaluation (Standish 2004, private communication),
improvements in Mercury's orbital parameters might amount to one
order of magnitude.
Indeed, the current accuracy in radar ranging is hundreds of
meters (Standish 2002), although the uncertainty in the planetary
topography further limits the realistic obtainable precision
(Pitjeva 1993); the new data could reach the tens of meters level
without the problems related to topography.
, BepiColombo (see
http://sci.esa.int/science-e/www/area/index.cfm?fareaid=30), which
is scheduled for
2010-2012. A complete error analysis for the
range and range-rate measurements can be found in Iess & Boscagli
(2001). According to them, a two orders of magnitude improvement
in the Earth-Mercury range should be possible. According to a more
conservative evaluation (Standish 2004, private communication),
improvements in Mercury's orbital parameters might amount to one
order of magnitude.
Indeed, the current accuracy in radar ranging is hundreds of
meters (Standish 2002), although the uncertainty in the planetary
topography further limits the realistic obtainable precision
(Pitjeva 1993); the new data could reach the tens of meters level
without the problems related to topography.
On the other hand, there would be severe limitations to the
possibility of detecting the Lense-Thirring effect by analyzing
the secular evolution of only one orbital element of a given
planet due to certain systematic aliasing errors.
Indeed, as in the case of the Earth-LAGEOS-LAGEOS II system, we
should cope with the multipolar expansion of the central mass,
i.e. the Sun in this case. The aliasing secular precessions
induced by its quadrupole mass moment J2 on the planetary nodes
and the perihelia would be almost one order of magnitude larger
than the Lense-Thirring precessions if we assume
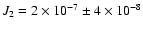 (Pireaux & Rozelot 2003). There are
still many uncertainties about the Sun's oblateness, both from a
theoretical modelling point of view and from an observational
point of view (Rozelot et al. 2004). Moreover, the perihelia are
also affected by another relevant post-Newtonian secular effect,
i.e. the gravitoelectric Einstein pericentre advance (Einstein
1915)
(Pireaux & Rozelot 2003). There are
still many uncertainties about the Sun's oblateness, both from a
theoretical modelling point of view and from an observational
point of view (Rozelot et al. 2004). Moreover, the perihelia are
also affected by another relevant post-Newtonian secular effect,
i.e. the gravitoelectric Einstein pericentre advance (Einstein
1915)
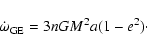 |
(2) |
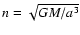 is the Keplerian mean motion of the orbiting
particle. This effect was measured for the first time in the Solar
System with the interplanetary ranging technique at a 10-3 level of
relative accuracy (Shapiro et al. 1972, 1976; Shapiro
1990). Recent observations yield a relative accuracy of
is the Keplerian mean motion of the orbiting
particle. This effect was measured for the first time in the Solar
System with the interplanetary ranging technique at a 10-3 level of
relative accuracy (Shapiro et al. 1972, 1976; Shapiro
1990). Recent observations yield a relative accuracy of
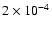 (Pitjeva 2001). The Einstein precession is almost four
orders of magnitude larger than the Lense-Thirring effect, so that
its mismodelled part would still be one order of magnitude larger
than the Lense-Thirring effect of interest. The classical N-body
secular precessions also are to be considered because they are
quite large (see Table 2).
(Pitjeva 2001). The Einstein precession is almost four
orders of magnitude larger than the Lense-Thirring effect, so that
its mismodelled part would still be one order of magnitude larger
than the Lense-Thirring effect of interest. The classical N-body
secular precessions also are to be considered because they are
quite large (see Table 2).
A possible solution could be to extend the Ciufolini-Iorio linear
combination approach to the Sun-planets scenario in order to built
up some combinations with the nodes of the inner planets which
cancel out the impact of the Sun's oblateness and of the N-body
precessions.
We give the expressions for the residuals of the nodes of Mercury,
Venus and Mars explicitly in terms of the mismodelled secular
precessions induced by the quadrupolar mass moment of the Sun,
the secular N-body precessions and of the Lense-Thirring secular
precessions, assumed as a totally unmodelled feature. It is
accounted for by a scaling parameter
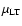 which is zero
in Newtonian mechanics and 1 in GTR
which is zero
in Newtonian mechanics and 1 in GTR![[*]](/icons/foot_motif.gif)
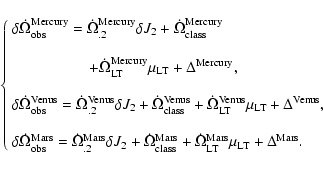 |
(3) |
The coefficients
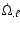 are defined as
are defined as
where
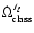 represent the classical
secular precessions induced by the oblateness of the central mass.
The coefficients
represent the classical
secular precessions induced by the oblateness of the central mass.
The coefficients
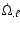 have been explicitly
worked out from
have been explicitly
worked out from 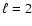 to
to 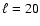 (Iorio 2003); they are
functions of the semimajor axis a, the inclination
(Iorio 2003); they are
functions of the semimajor axis a, the inclination![[*]](/icons/foot_motif.gif) i and the eccentricity e of the
considered planet:
i and the eccentricity e of the
considered planet:
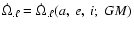 .
For the first two even zonal harmonics we have
.
For the first two even zonal harmonics we have
![\begin{displaymath}\left\{\begin{array}{lll}
\dot\Omega_{.2}=-\frac{3}{2}n\left(...
...{(1-e^2)^2}
\left(7\sin^2 i-4\right)\right];
\end{array}\right.\end{displaymath}](/articles/aa/full/2005/07/aa1646/img80.gif) |
(4) |
R is the Sun's equatorial
radius. The quantities 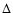 in Eq. (3) refer to the other
unmodelled or mismodelled effects which affect the temporal
evolution of the nodes of the considered planets. In the present
case they would mainly be represented by the precessions induced
by the octupolar mass moment of the Sun (Rozelot et al. 2004).
From the results of Table 2 and from the evaluations of
Rozelot et al. (2004) according to which the possible magnitude of
J4 would span the range
10-7-10-9, the secular
precession induced by the octupolar mass moment of the Sun is
negligible with respect the Lense-Thirring rates. These facts lead
us to design a three-node combination which cancels out the
effects of J2 and of the classical N-body precessions while
it is affected by the residual effect of J4.
in Eq. (3) refer to the other
unmodelled or mismodelled effects which affect the temporal
evolution of the nodes of the considered planets. In the present
case they would mainly be represented by the precessions induced
by the octupolar mass moment of the Sun (Rozelot et al. 2004).
From the results of Table 2 and from the evaluations of
Rozelot et al. (2004) according to which the possible magnitude of
J4 would span the range
10-7-10-9, the secular
precession induced by the octupolar mass moment of the Sun is
negligible with respect the Lense-Thirring rates. These facts lead
us to design a three-node combination which cancels out the
effects of J2 and of the classical N-body precessions while
it is affected by the residual effect of J4.
Indeed, if we solve Eq. (3) for the Lense-Thirring parameter
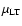 it is possible to obtain
it is possible to obtain
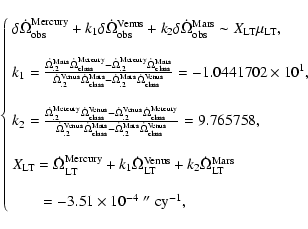 |
(5) |
where the
numerical values of the coefficients k1 and k2 and the slope
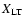 of the gravitomagnetic trend come from the values of
Table 2. We construct the time series of the residuals of
the nodes of Mercury, Venus and Mars by using real observational
data and the full dynamical models in which GTR is purposely set
equal to zero, e.g. by using a very large value of c. We expect
that, over a multidecade observational time span, the combined
residuals will fully show the GTR signature
in terms of
a linear trend. The measured slope, divided by
of the gravitomagnetic trend come from the values of
Table 2. We construct the time series of the residuals of
the nodes of Mercury, Venus and Mars by using real observational
data and the full dynamical models in which GTR is purposely set
equal to zero, e.g. by using a very large value of c. We expect
that, over a multidecade observational time span, the combined
residuals will fully show the GTR signature
in terms of
a linear trend. The measured slope, divided by
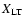 ,
yields
,
yields
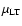 which should be equal to one if GTR is
correct and if the bias from the residual N-body effect was
sufficiently small. The systematic error affecting
Eq. (6) is negligible because it would be due only to the
higher degree multipole mass moments of the Sun. The obtainable
1-sigma observational error, according to the results of Table
3, would amount to 36
which should be equal to one if GTR is
correct and if the bias from the residual N-body effect was
sufficiently small. The systematic error affecting
Eq. (6) is negligible because it would be due only to the
higher degree multipole mass moments of the Sun. The obtainable
1-sigma observational error, according to the results of Table
3, would amount to 36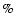 .
.
In this paper we have explored the possibility of measuring the
post-Newtonian Lense-Thirring effect induced by the solar
gravitomagnetic field on the motion of some of the Solar System
planets. The magnitude of the gravitomagnetic precessions is very
small, 10-3 '' cy-1 for Mercury. The main systematic errors
which would mask the relativistic effect of interest would be the
quite larger secular precessions induced by the post-Newtonian
gravitoelectric part of the Sun's gravitational field, by the
Sun's oblateness and by the N-body interactions. By using a
suitably designed linear combination of the orbital residuals of
the nodes of Mercury, Venus and Mars it would be possible to
cancel out the corrupting impact of the first solar even zonal
harmonic plus the N-body classical secular precessions.
Moreover, the proposed measurement would not be aliased by the
post-Newtonian gravitoelectric field because it affects only the
perihelia and the mean anomalies. The obtainable observable
accuracy should be 36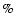 (1-sigma) for the proposed
J2-(N-body) free combination. It would be a somewhat modest
result for a reliable test of GTR. However, we note that should
new, more accurate ephemerides for Mercury be available as a
by-product of the Messenger and, especialy, BepiColombo missions,
the error's evaluation presented here could become more favorable.
(1-sigma) for the proposed
J2-(N-body) free combination. It would be a somewhat modest
result for a reliable test of GTR. However, we note that should
new, more accurate ephemerides for Mercury be available as a
by-product of the Messenger and, especialy, BepiColombo missions,
the error's evaluation presented here could become more favorable.
Acknowledgements
L. Iorio is grateful to E. M. Standish (JPL) and E. V. Pitjeva
(Institute of Applied Astronomy of Russian Academy of Sciences),
for their help and useful discussions and clarifications, and to
W.-T. Ni (Purple Mountain Observatory) for the updated reference
to ASTROD.
-
Ciufolini, I. 1986, Phys. Rev. Lett., 56, 278 [NASA ADS] [CrossRef] (In the text)
-
Ciufolini, I. 1996, Il Nuovo Cimento A, 109, 1709 (In the text)
-
Ciufolini, I., Pavlis, E. C., Chieppa, F., Fernandes-Vieira, E.,
& Pérez-Mercader, J. 1998, Science, 279, 2100 [NASA ADS] [CrossRef] (In the text)
- Einstein,
A. 1915, Preuss. Akad. Wiss. Berlin Sitzber., 47, 831 (In the text)
-
Estabrook, F. 1971, JPL IOM, Sect. 328, 1
- Everitt, C.
F. W., Buchman, S., DeBra, D. B., and other members of the Gravity
Probe B Team 2001, Gravity Probe B: Countdown to Launch. In Gyros,
Clocks, and Interferometers: Testing Relativistic Gravity in Space,
ed. C. Lämmerzahl, C. W. F. Everitt, & F.W. Hehl
(Springer-Verlag, Berlin), 52
(In the text)
- Iess, L., &
Boscagli, G. 2001, Plan. Space Sci., 49, 1597 [NASA ADS] [CrossRef] (In the text)
- Iorio, L. 2002,
Class. Quantum Grav., 19, 5473 [NASA ADS] [CrossRef] [MathSciNet] (In the text)
- Iorio,
L., Lucchesi, D.M., & Ciufolini, I. 2002, Class. Quantum Grav.,
19, 4311 [NASA ADS] [CrossRef] (In the text)
- Iorio, L. 2003,
Celest. Mech & Dyn. Astron., 86, 277 [NASA ADS] (In the text)
- Iorio, L., &
Morea, A. 2004, Gen. Rel. Gravit., 36, 1321 [NASA ADS] (In the text)
- Iorio,
L., Ciufolini, I., Pavlis, E.C., et al. 2004, Class. Quantum Grav.,
21, 2139 [NASA ADS] [CrossRef] (In the text)
- Lense, J., &
Thirring, H. 1918, Phys. Z. 19, 156, translated by Mashhoon, B.,
Hehl, F. W., & Theiss, D. S. 1984, Gen. Rel. Grav., 16,
711 [CrossRef] [MathSciNet] (In the text)
- Milani, A.,
Vokrouhlick
 , D., Villani, D., Bonanno, C. & Rossi, A. 2002,
Phys. Rev. D., 66, 082001 [NASA ADS] [CrossRef]
, D., Villani, D., Bonanno, C. & Rossi, A. 2002,
Phys. Rev. D., 66, 082001 [NASA ADS] [CrossRef] - Ni, W.-T., Shiomi, S.,
& Liao, A.-C. 2004, Class. Quantum Grav., 21, S641 [CrossRef] (In the text)
-
Nordtvedt, K. 2003, Some considerations on the varieties of frame
dragging. In Nonlinear Gravitodynamics. The Lense-Thirring Effect,
ed. R. Ruffini, & C. Sigismondi (Singapore: World Scientific),
35
(In the text)
- Pijpers, F.
P. 2003, A&A, 402, 683 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Pireaux, S.,
& Rozelot, J.-P. 2003, Ap&SS, 284, 1159 [NASA ADS] (In the text)
- Pitjeva, E.
V. 1993, Celest. Mech. & Dyn. Astron., 55, 313 [NASA ADS] (In the text)
- Pitjeva, E.
V. 2001, Celest. Mech. & Dyn. Astron., 80, 249 [NASA ADS] (In the text)
- Ries, J. C., Eanes,
R. J., & Tapley, B. D. 2003, Lense-Thirring Precession
Determination from Laser Ranging to Artificial Satellites. In
Nonlinear Gravitodynamics. The Lense-Thirring Effect, ed. R.
Ruffini, & C. Sigismondi, (Singapore: World Scientific),
201
(In the text)
-
Rozelot, J.-P., Pireaux, S., Lefebvre, S., & Corbard, T. 2004,
preprint [arXiv:astro-ph/0403382]
(In the text)
- Schiff, L.I.
1960, Am. J. Phys., 28, 340 [MathSciNet] (In the text)
- Shapiro, I.,
Pettengill, G. H., Ash, M. E., et al. 1972, Phys Rev. Lett., 28,
1594 [NASA ADS] [CrossRef] (In the text)
- Shapiro, I.,
Counselman, C., & King, R. 1976, Phys Rev. Lett., 36, 555 [NASA ADS] [CrossRef] (In the text)
- Shapiro, I.
1990, Solar system tests of general relativity: recent results and
present plans, In Proc. 12th International Conf. General Relativity
and Gravitation, ed. N. Ashby, D. Bartlett, & W. Wyss
(Cambridge: Cambridge University Press), 313
(In the text)
- Standish,
E. M. 1998, JPL planetary and lunar ephemerides DE405/LE405,
Interoffice Memorandum 312.F-98-048, 1
(In the text)
- Standish,
E. M. 2002, Future JPL Ephemerides, In Proc. IERS Workshop on the
Implementation of the New IAU Resolutions, IERS Technical Note No.
29, ed. N. Capitaine, D. Gambis, D. D. McCarthy, G. Petit, J. Ray,
B. Richter, M. Rothacher, E. M. Standish, & J. Vondrak
(Frankfurt am Main: Verlag des Bundesamts f
 r Kartographie und Geod
r Kartographie und Geod
 sie), 61
(In the text)
sie), 61
(In the text) - Turyshev,
S. G., Shao, M., & Nordtvedt, K. 2004, Class. Quantum Grav.,
21, 2773 [NASA ADS] [CrossRef] (In the text)
- Will, C. M. 1993,
Theory and Experiment in Gravitational Physics, 2nd edition
(Cambridge: Cambridge University Press)
(In the text)
Copyright ESO 2005
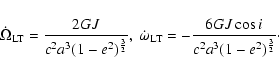
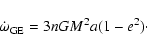
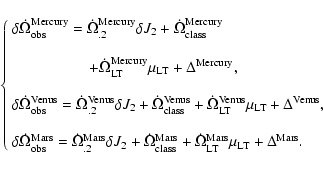
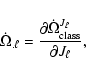
![\begin{displaymath}\left\{\begin{array}{lll}
\dot\Omega_{.2}=-\frac{3}{2}n\left(...
...{(1-e^2)^2}
\left(7\sin^2 i-4\right)\right];
\end{array}\right.\end{displaymath}](/articles/aa/full/2005/07/aa1646/img80.gif)