- ...
force
![[*]](/icons/foot_motif.gif)
- According to Nordtvedt (2003), the Earth-Moon
range is affected by long-periodic harmonic perturbations of
gravitomagnetic origin whose amplitudes are of the order of 5 m
and the periods are monthly and semi-monthly. The amplitudes of
the lunar motion at both these periods are determined to better
than half a centimeter precision in the total orbital fit to the
LLR data.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... origin
![[*]](/icons/foot_motif.gif)
- In the case of the LAGEOS-LAGEOS II
experiment in the gravitational field of the Earth, the
non-gravitational effects also play a very important role,
especially in perturbing the perigee of LAGEOS II. In the case of
planetary motions the non-conservative forces are, instead,
irrelevant.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... harmonics
![[*]](/icons/foot_motif.gif)
- In general, they are the first low-degree
ones J2, J4,...
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... evolution
![[*]](/icons/foot_motif.gif)
- Here we speak
about nodal residuals in a, strictly speaking, improper sense. The
Keplerian orbital elements are not directly observable: they can
only be computed (in the case of the Solar System bodies
exhibiting small inclinations the nodes should be obtained by the
currently used parameters
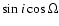 and
and
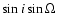 ). The basic observable quantities are ranges,
range-rates and angles. Here we mean the differences between the
time series of the node computed from a given observed orbital arc
and the time series of the node computed from a propagated orbital
arc with the gravitomagnetic force switched off in the force
models. The two time series share the same initial conditions.
Note that the post-Newtonian equations of motion used at JPL for
the computation of the planetary ephemerides (Estabrook 1971) do
not include the gravitomagnetic force, so that the Lense-Thirring
effect would automatically be absorbed in the time series of
). The basic observable quantities are ranges,
range-rates and angles. Here we mean the differences between the
time series of the node computed from a given observed orbital arc
and the time series of the node computed from a propagated orbital
arc with the gravitomagnetic force switched off in the force
models. The two time series share the same initial conditions.
Note that the post-Newtonian equations of motion used at JPL for
the computation of the planetary ephemerides (Estabrook 1971) do
not include the gravitomagnetic force, so that the Lense-Thirring
effect would automatically be absorbed in the time series of
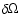 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... especially
![[*]](/icons/foot_motif.gif)
- While the spacecraft trajectory
will be determined from the range-rate data, the planet's orbit
will be retrieved from the range data (Milani et al. 2002). In
particular, the determination of the planetary centre of mass is
important for this goal which can be better reached by a not too
elliptical spacecraft orbit. The relatively moderate ellipticity
of the planned
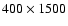 km polar orbit of BepiColombo,
contrary to the much more elliptical path of Messenger, is, then,
appropriate.
km polar orbit of BepiColombo,
contrary to the much more elliptical path of Messenger, is, then,
appropriate.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... GTR
![[*]](/icons/foot_motif.gif)
- It can be shown that
it can be expressed in terms of the PPNparameter
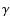 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... inclination
![[*]](/icons/foot_motif.gif)
- As
pointed out in Milani et al. (2002), the angle i refers to the
inclination between the planet's orbital plane and the fixed
reference plane of the celestial reference frame; it is not the
angle
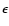 between the planet's orbital plane and the
ecliptic. It turns out that
between the planet's orbital plane and the
ecliptic. It turns out that
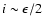 .
For Mercury
.
For Mercury
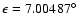 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.