A&A 430, 603-628 (2005)
DOI: 10.1051/0004-6361:20041659
L. Di Fabrizio1,2 - G. Clementini1 - M. Maio1 - A. Bragaglia1 - E. Carretta1,3 - R. Gratton3 - P. Montegriffo1 - M. Zoccali4,5
1 - INAF - Osservatorio Astronomico di Bologna, Via Ranzani 1,
40127 Bologna, Italy
2 -
INAF - Centro Galileo Galilei & Telescopio Nazionale Galileo,
PO Box 565,
38700 S.Cruz de La Palma, Spain
3 -
INAF - Osservatorio Astronomico di Padova, Vicolo dell'Osservatorio 5, 35122
Padova, Italy
4 - Pontificia Universidad Católica de Chile, Departado de Astronomía
y Astrofísica, Av. Vicuna Mackenna 4860, 782-0436, Macul, Santiago, Chile
5 -
Princeton University Observatory, Peyton Hall,
Princeton NJ 08544, USA
Received 14 July 2004 / Accepted 27 September 2004
Abstract
The catalogue of the Johnson-Cousins B,V and I light curves
obtained for 162
variable stars (135 RR Lyrae, 4 candidate Anomalous Cepheids, 11 Classical Cepheids,
11 eclipsing binaries and 1 ![]() Scuti star) in two areas close to the bar of the Large Magellanic Cloud is
presented along with coordinates, finding charts, periods, epochs,
amplitudes, and mean
quantities
(intensity- and magnitude-averaged luminosities) of the variables with full
coverage of the
light variations.
A star by star comparison is made with MACHO and OGLE II photometries based
on both
variable and constant stars in common, and the
transformation relationships to our photometry are provided.
The pulsation properties of the RR Lyrae stars in the sample are discussed in
detail.
Parameters of the Fourier decomposition of the light curves are derived
for the fundamental
mode RR Lyrae stars with complete and regular curves (29 stars).
They are
used to estimate metallicities, absolute magnitudes,
intrinsic (B-V)0 colours, and temperatures of the variable stars, according
to Jurcsik & Kovács (1996, A&A, 312, 111), and Kovács & Walker (2001, A&A, 371, 579) method. Quantities derived
from the Fourier parameters are compared with
the corresponding observed quantities. In particular,
the "photometric'' metallicities are compared with the spectroscopic
metal abundances derived by Gratton et al. (2004, A&A, 421, 937) from low
resolution spectra obtained with FORS at the Very Large Telescope.
Scuti star) in two areas close to the bar of the Large Magellanic Cloud is
presented along with coordinates, finding charts, periods, epochs,
amplitudes, and mean
quantities
(intensity- and magnitude-averaged luminosities) of the variables with full
coverage of the
light variations.
A star by star comparison is made with MACHO and OGLE II photometries based
on both
variable and constant stars in common, and the
transformation relationships to our photometry are provided.
The pulsation properties of the RR Lyrae stars in the sample are discussed in
detail.
Parameters of the Fourier decomposition of the light curves are derived
for the fundamental
mode RR Lyrae stars with complete and regular curves (29 stars).
They are
used to estimate metallicities, absolute magnitudes,
intrinsic (B-V)0 colours, and temperatures of the variable stars, according
to Jurcsik & Kovács (1996, A&A, 312, 111), and Kovács & Walker (2001, A&A, 371, 579) method. Quantities derived
from the Fourier parameters are compared with
the corresponding observed quantities. In particular,
the "photometric'' metallicities are compared with the spectroscopic
metal abundances derived by Gratton et al. (2004, A&A, 421, 937) from low
resolution spectra obtained with FORS at the Very Large Telescope.
Key words: stars: fundamental parameters - stars: variables: general - stars: variables: RR Lyrae - galaxies: individual: LMC - techniques: photometric
Table 1: Journal of the photometric observations.
We have obtained accurate multiband time series photometry reaching
![]() (i.e.
(i.e. ![]() 3.5 mag fainter than the RR Lyrae stars in the LMC) of two 13
3.5 mag fainter than the RR Lyrae stars in the LMC) of two 13
![]() fields close to the bar of the LMC
and studied their variable stars (135 RR Lyrae, 4 candidate Anomalous
Cepheids, 11 Classical Cepheids, 11 eclipsing binaries, and 1
fields close to the bar of the LMC
and studied their variable stars (135 RR Lyrae, 4 candidate Anomalous
Cepheids, 11 Classical Cepheids, 11 eclipsing binaries, and 1 ![]() Scuti).
The photometric data were complemented by spectroscopic observations
obtained with the 3.6 m and the VLT ESO telescopes in 1999 and 2001, respectively,
and used to derive
individual metallicities
for 101
of the variables in the present sample,
and the luminosity-metallicity relation
(
Scuti).
The photometric data were complemented by spectroscopic observations
obtained with the 3.6 m and the VLT ESO telescopes in 1999 and 2001, respectively,
and used to derive
individual metallicities
for 101
of the variables in the present sample,
and the luminosity-metallicity relation
(
![]() )
of the LMC
RR Lyrae stars (Bragaglia et al. 2001; Clementini et al. 2003a, hereinafter C03;
Gratton et al. 2004, hereinafter G04).
A discussion of
the astrophysical impact of the new data on the derivation of the
)
of the LMC
RR Lyrae stars (Bragaglia et al. 2001; Clementini et al. 2003a, hereinafter C03;
Gratton et al. 2004, hereinafter G04).
A discussion of
the astrophysical impact of the new data on the derivation of the
![]() relationship and
on the definition of the distance to the LMC has been presented
in C03.
relationship and
on the definition of the distance to the LMC has been presented
in C03.
In this paper we present
the catalogue of the B,V,I light curves obtained for the 162 short period variables we have identified in the two fields.
In Sect. 2 we describe the acquisition, reduction and calibration of the
data. Section 3 describes the identification, the period search procedures
and the characteristics of the variables. In Sect. 4 we present the star-by-star
comparison with MACHO and OGLE II photometries, based on both variable and constant
stars in common, and provide transformation relationships. The
period distribution and the period amplitude relations followed by the RR Lyrae
stars in our sample are discussed in Sect. 5. In Sect. 6 we discuss
the metallicities, absolute
magnitudes, intrinsic (B-V)0 colours, and effective temperatures
derived from the the Fourier
decomposition of the light curve of the ab-type RR Lyrae stars
with regular
light curves (29 stars) and compare them with the corresponding
observed quantities.
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{1659fig1.ps} %\end{figure}](/articles/aa/full/2005/05/aa1659/Timg20.gif) |
Figure 1: The light squares indicate the approximate positions of our observed fields with respect to MACHO's fields #6 and #13. The elongated rectangle identifies the position of the OGLE II field LMC_SC21. North is up and East is left. |
| Open with DEXTER | |
The photometric observations presented in this paper were carried out at the 1.54 m Danish telescope located in La Silla, Chile, on the nights 4-7 January 1999, UT, and 23-24 January 2001, UT, respectively. The journal of the photometric observations is provided in Table 1 along with information about sky conditions during the observations.
In both observing runs we centered our observations at two different positions, hereinafter called fields A and B, close to the bar of the LMC and contained in fields #6 and #13 of the MACHO microlensing experiment (see A96 and the MACHO web site at http://wwwmacho.mcmaster.ca). Field A turned out also to have an about 40% overlap with OGLE II field LMC_SC21 (Udalsky et al. 2000). The observed fields and their positions with respect to MACHO's map of the LMC are shown in Fig. 1, where the elongated rectangle indicates the position of the OGLE II field LMC_SC21.
The two positions were chosen in order to maximize the number of
known RRd's observable with only two pointings of the 1.54 m Danish telescope,
since a major purpose of our study was to derive the
mass-metallicity relation for double mode pulsators (Bragaglia et al. 2001).
We expected to observe about 80 RR Lyrae's according to A96 average density of
RR Lyr's in the LMC, among which 5 and 4 double mode RR Lyrae (RRd), in field A
and B, respectively (Alcock et al. 1997,
hereinafter A97). Coordinates
(epoch 2000) of the two centers are:
![]() :22:48.49,
:22:48.49,
![]() :34:06 (field A), and
:34:06 (field A), and
![]() :17:35.7,
:17:35.7,
![]() :00:13
(field B). In both observing runs the telescope was equipped with the DFOSC focal
reducer. In 1999 data were acquired on a Loral/Lesser
:00:13
(field B). In both observing runs the telescope was equipped with the DFOSC focal
reducer. In 1999 data were acquired on a Loral/Lesser
![]() pixel
chip (CCD #C1W7, scale 0.4 arcsec/pix, field of view of 13.7 arcmin2), and a filter wheel mounting the Johnson standard system.
Observations were done in the Johnson-Bessel B and V filters (ESO 450,
and 451), and we obtained 58 Vand 27 B frames for field A, and 55 V and 24 B frames for field B.
Seeing conditions were quite variable during each night and the whole
observing run; typical
values were in the range 1.3-1.9 arcsec (see Table 1)
pixel
chip (CCD #C1W7, scale 0.4 arcsec/pix, field of view of 13.7 arcmin2), and a filter wheel mounting the Johnson standard system.
Observations were done in the Johnson-Bessel B and V filters (ESO 450,
and 451), and we obtained 58 Vand 27 B frames for field A, and 55 V and 24 B frames for field B.
Seeing conditions were quite variable during each night and the whole
observing run; typical
values were in the range 1.3-1.9 arcsec (see Table 1)![]() .
.
Exposure times varied from 180 to 300 s in V and from 360 to 480 s in B, depending on weather/seeing conditions and hour angle. They were chosen as an optimal compromise between S/N and time resolution of the light variations of the RR Lyrae variables. Eighteen stars from Landolt (1992) standard fields were observed during each night in order to secure the transformation to the standard Johnson photometric system.
In the 2001 run, data were acquired on an EEV 42-80 CCD (
![]() pixels,
scale of 0.39 arcsec/pix and field of view of 13.7 arcmin2). The CCD
has pixel size of 15
pixels,
scale of 0.39 arcsec/pix and field of view of 13.7 arcmin2). The CCD
has pixel size of 15 ![]() m and is back-illuminated to increase its quantum
efficiency, particularly at shorter wavelengths. Due to the field of view
of the
DFOSC focal reducer, only half of the CCD is actually used to image
data. Observations were done in the Johnson-Bessel B, V and in the
i-Gunn
filters
m and is back-illuminated to increase its quantum
efficiency, particularly at shorter wavelengths. Due to the field of view
of the
DFOSC focal reducer, only half of the CCD is actually used to image
data. Observations were done in the Johnson-Bessel B, V and in the
i-Gunn
filters![]() (ESO 450, 451, and 425)
and we obtained 14 V, 14 B and 14 i frames for
field A, and 15 V, 14 B, and 14 i frames for field B. Exposure times
were of 360 s in B, and 180 s in V and i.
(ESO 450, 451, and 425)
and we obtained 14 V, 14 B and 14 i frames for
field A, and 15 V, 14 B, and 14 i frames for field B. Exposure times
were of 360 s in B, and 180 s in V and i.
Both nights of the 2001 run were fully photometric with good seeing conditions. Transparency and seeing were better in the second night with most frequent values of the seeing around 1.0 arcsec in B and V, and 0.8 arcsec in i. A large number of standard stars in Landolt (1992) - Stetson (2000) standard fields PG 0918+029, PG 0231+051, PG 1047+003, and SA98 were observed several times during both nights to estimate the nightly extinction and to tie the observations to the standard Johnson-Cousins photometric system (see Sect. 2.2). Two exposures of different length were taken at any pointings of the standard fields, in order to obtain well exposed measurements of both bright and faint standard stars.
Reduction and analysis of the 1999 photometric data were done using the
package DoPHOT (Schechter et al. 1993), which uses an elliptical
Gaussian PSF to evaluate instrumental magnitudes. We used a PSF
varying with the position on the frame and
run DoPHOT independently on all frames, with a threshold for source detection
of 5![]() above the local sky. The resulting tables were then aligned to
the "best" frame for
each field (i.e., to the one taken in best seeing and weather conditions, and
near meridian) and stars were counteridentified
using a private software written by P.
Montegriffo. Catalogues were produced, all
containing the same number of stars, and with a unique identifying number: this
helped in the following variability search and study. The number of objects
classified as stars in each frame is variable (from several thousands to about
30 000). The final 1999 catalogues, after counteridentification in V and B,
contain about 29 000 objects for field A and about 23 000 for field B; this
difference seems reasonable since field A is slightly closer to the LMC bar and thus more
crowded than field B.
above the local sky. The resulting tables were then aligned to
the "best" frame for
each field (i.e., to the one taken in best seeing and weather conditions, and
near meridian) and stars were counteridentified
using a private software written by P.
Montegriffo. Catalogues were produced, all
containing the same number of stars, and with a unique identifying number: this
helped in the following variability search and study. The number of objects
classified as stars in each frame is variable (from several thousands to about
30 000). The final 1999 catalogues, after counteridentification in V and B,
contain about 29 000 objects for field A and about 23 000 for field B; this
difference seems reasonable since field A is slightly closer to the LMC bar and thus more
crowded than field B.
Photometric reductions of the 2001 data were done using DAOPHOT/ALLSTAR II
(Stetson 1996) and ALLFRAME (Stetson 1994). DAOPHOT/ALLSTAR II allows to
obtain very precise brightness estimates and astrometric positions for stellar
objects in individual two-dimensional digital images starting from a rough
initial estimate for the position and brightness of each star, and a model of
the PSF for each frame. We used a source detection threshold of 4![]() above the local sky background, and a PSF which varied quadratically with
the position in the frame. Modelling of the PSF in each frame was obtained by
considering a set of about 100 stars. The resulting PSFs are hybrid models
consisting of an analytic function and a table of residuals,
thus offering both the advantages of an analytic and of an empirical PSF.
above the local sky background, and a PSF which varied quadratically with
the position in the frame. Modelling of the PSF in each frame was obtained by
considering a set of about 100 stars. The resulting PSFs are hybrid models
consisting of an analytic function and a table of residuals,
thus offering both the advantages of an analytic and of an empirical PSF.
Because of the high crowding of our LMC fields, in addition to DAOPHOT/ALLSTAR, reductions were executed with ALLFRAME, which performed the simultaneous consistent reductions of all the 2001 multicolour images of our fields: 42 frames for field A, and 43 frames for field B, respectively. By combining informations coming from all images it was thus possible to obtain a better precision in the identification and centering of the stars, and to resolve objects that appeared blended in frames with worse seeing conditions.
Aperture corrections were derived for the B, V, I reference frames from about 10 bright and relatively isolated stars in each frame. The choice of these stars has been particularly difficult for field A, the more crowded one, for which we also derived larger corrections. The mean differences between PSF and aperture magnitudes were used to correct the PSF magnitudes of all other objects. The B, V, I corrections (aperture minus PSF) were: -0.140, -0.073, -0.020 mag for field A, and -0.026, -0.035, -0.040 mag for field B respectively.
Aperture magnitudes for the photometric standard stars were computed using PHOT in DAOPHOT, rejecting all saturated stars and all objects with less than 1000 detected counts. The aperture radii for these stars were determined from curves of growth.
The extinction coefficients for the nights were computed from
observations of the
standard
stars in the selected areas PG 0918+029 and SA98 (Landolt 1992). We used 7 bright
standard stars
in PG 0918, with measurements at different airmasses (
![]() )
to
estimate the extinction coefficients for the night of January 23, and
7 bright standard stars of SA98 with measurements at
)
to
estimate the extinction coefficients for the night of January 23, and
7 bright standard stars of SA98 with measurements at
![]() ,
to estimate the extinction for the night of January 24. The derived first
order extinction coefficients are:
,
to estimate the extinction for the night of January 24. The derived first
order extinction coefficients are:
![]() ,
,
![]() ,
and
,
and
![]() for January 23;
for January 23;
![]() ,
,
![]() ,
and
,
and
![]() for January 24.
These extinction coefficients well compare to the average ones for La Silla,
as deduced from the relevant web pages.
for January 24.
These extinction coefficients well compare to the average ones for La Silla,
as deduced from the relevant web pages.
Stetson (2000) has extended Landolt (1992) standard fields to a fainter
magnitude limit, reaching ![]() mag. To transform to the standard
Johnson-Cousins photometric system, we used Stetson (2000) standard star
magnitudes, as available from the web site
http://cadcwww.hia.nrc.ca/standards, for a large number of standards in
Landolt's fields PG 0918+029, PG 0231+051, PG 1047+003, and SA98. We have
verified that Stetson (2000) standard system reproduces very well the
Johnson-Cousins standard system by Landolt (1992).
In fact, if we restrict only to the original Landolt standards in each field,
and derive the calibrating equations using both Landolt's and Stetson's values,
the colour terms agree to the thousandth of magnitude both in B and V.
In I there
are two deviating stars, namely PG 0231 for which Landolt's I magnitude is
about 0.2 mag too bright, and SA98-1002 whose Landolt's I magnitude is about
0.02-0.04 mag fainter. If these two stars are discarded, agreement to within a
thousandth of magnitude is found for the I colour terms as well.
mag. To transform to the standard
Johnson-Cousins photometric system, we used Stetson (2000) standard star
magnitudes, as available from the web site
http://cadcwww.hia.nrc.ca/standards, for a large number of standards in
Landolt's fields PG 0918+029, PG 0231+051, PG 1047+003, and SA98. We have
verified that Stetson (2000) standard system reproduces very well the
Johnson-Cousins standard system by Landolt (1992).
In fact, if we restrict only to the original Landolt standards in each field,
and derive the calibrating equations using both Landolt's and Stetson's values,
the colour terms agree to the thousandth of magnitude both in B and V.
In I there
are two deviating stars, namely PG 0231 for which Landolt's I magnitude is
about 0.2 mag too bright, and SA98-1002 whose Landolt's I magnitude is about
0.02-0.04 mag fainter. If these two stars are discarded, agreement to within a
thousandth of magnitude is found for the I colour terms as well.
We measured magnitudes for 67 stars in these areas. However, since most of the
new faint standard stars observed by Stetson (2000) only have Vmeasurements, while the B and I database is still poor, only a subset of 27
stars with accurate standard magnitudes in all three photometric pass-bands of
our interest were actually used in the calibration procedure. Aperture
photometry magnitudes of these stars measured in the two nights of the 2001
run, corrected for the extinction appropriate to each night, were combined
to derive
the following calibration equations:
![\begin{eqnarray*}&&\hspace*{-3.5mm} B-b = 0.111 (\pm 0.032) \times (b-v) - 5.472...
... = -0.023 (\pm 0.025) \times (v-i) - 6.507 \nonumber \\ [-8mm] %
\end{eqnarray*}](/articles/aa/full/2005/05/aa1659/img37.gif)
Figure 2 shows the instrumental colour magnitude diagrams (CMDs)
obtained from the
photometric reductions of one V and one B frames of field A, from the
1999 and 2001 data sets
respectively, using the various different packages employed in this study,
namely DoPhot for the 1999 data set (left panel),
DAOPHOT + ALLSTAR (central panel),
and DAOPHOT + ALLSTAR + ALLFRAME (right panel) for the
2001 data set.
![\begin{figure}
\par\includegraphics[width=8.7cm,clip]{1659fig2.ps}
\end{figure}](/articles/aa/full/2005/05/aa1659/Timg38.gif) |
Figure 2: Comparison between instrumental CMDs (all based on two frames) of the 1999 and 2001 datasets. Left panel: DoPhot reductions of the 1999 data; central panel: DAOPHOT+ALLSTAR reductions of the 2001 data; right panel: DAOPHOT+ALLSTAR+ALLFRAME reductions of the 2001 data. |
| Open with DEXTER | |
Variable stars were identified on the 1999 vand b instrumental time-series independently, using the
program VARFIND, by P. Montegriffo. VARFIND performs the following actions:
(i) normalizes the files containing measures of the fitted stars to a
reference frame, using
all stars in 1.5 mag bins about 2 mag brighter than the
expected average level of the RR Lyrae variables to
determine mean frame-to-frame offsets with respect to the reference
frames. As v and b reference frames we chose those taken
in the best seeing and photometric conditions; (ii) computes the average magnitude of each star and its standard
deviation by combining all frames in a given filter, using the offsets
determined in step (i); (iii) displays the scatter diagrams of the average
measurements, namely the standard deviations vs. average
![]() and
and
![]() plots
from which candidate variables are identified thanks to their large
rms and picked up interactively. In our scatter diagrams the
RR Lyrae's and the Cepheids define very well distinct groups
of stars with large rms values, respectively at
18.6<V<19.8 mag and
15.1<V<16.6 mag;
(iv) extracts the time-series sequence of each candidate variable and of its
selected reference stars (see below).
plots
from which candidate variables are identified thanks to their large
rms and picked up interactively. In our scatter diagrams the
RR Lyrae's and the Cepheids define very well distinct groups
of stars with large rms values, respectively at
18.6<V<19.8 mag and
15.1<V<16.6 mag;
(iv) extracts the time-series sequence of each candidate variable and of its
selected reference stars (see below).
The search procedure was repeated several
times, subsequently lowering the detection threshold. Stars whose standard
deviations of the
![]() and
and
![]() measurements were larger than 3
measurements were larger than 3![]() ,
where
,
where ![]() is the rms of bona-fide non-variable stars at same magnitude level,
were flagged as candidate variables and closely inspected for
variability using the program
GRATIS (GRaphycal Analyzer of TIme Series) a private software developed at the
Bologna Observatory by P. Montegriffo, G. Clementini and L. Di Fabrizio.
This code, directly interfaced to VARFIND, allows to display the sequence
of differential measurements of the object with respect to the selected
reference stable stars, as a function of the Heliocentric Julian day of
observation, and to perform a period search on these data (see below).
A total number of 1165 and 747 objects were checked for variability in fields A
and B, respectively. We are confident that our identification of the RR
Lyrae stars is rather complete, and
we will come back to this point in Sects. 3.2 and 5.
is the rms of bona-fide non-variable stars at same magnitude level,
were flagged as candidate variables and closely inspected for
variability using the program
GRATIS (GRaphycal Analyzer of TIme Series) a private software developed at the
Bologna Observatory by P. Montegriffo, G. Clementini and L. Di Fabrizio.
This code, directly interfaced to VARFIND, allows to display the sequence
of differential measurements of the object with respect to the selected
reference stable stars, as a function of the Heliocentric Julian day of
observation, and to perform a period search on these data (see below).
A total number of 1165 and 747 objects were checked for variability in fields A
and B, respectively. We are confident that our identification of the RR
Lyrae stars is rather complete, and
we will come back to this point in Sects. 3.2 and 5.
Variable stars were then counteridentified on the 2001 frames using private software by P. Montegriffo. A few further variables originally missed by the search on the 1999 data were recovered in the comparison with MACHO and OGLE II datasets (see Sect. 4). In the end the two fields were found to contain a total number of 162 short period variable stars (P< 7 days), mainly of RR Lyrae type (125 single-mode and 10 double-mode, one of which not previously known from A97; see Sect. 5.1), and an additional 8 candidate variable objects: 5 possible binary systems, 1 possible ab-type RR Lyrae, and 2 other variables that we were not able to classify.
The number of variables divided by type and field is given in Table 2.
Table 2: Number and type of variables identified in the two fields.
Finding charts for all the variables are provided in Figs. 3 to 10 only available in the electronic version, where each field is divided in 4 quadrants 6.8
All variables were studied using their differential photometry with respect to
two stable, well isolated objects used as reference stars, whose constancy was
carefully checked on the full 1999-2001 data set. Coordinates and calibrated
magnitudes of the reference stars from the 2001 photometry
are given in Table 3. Errors quoted in the table include both the internal
error contribution given by ALLFRAME (about 0.005 mag in V and I, and 0.004 mag in B), and
the systematic errors in the transformation to the standard system (which include
uncertainties of the aperture corrections: about 0.02 mag in V and I and
0.03 mag in B, and the zero points of the photometric calibration: ![]() mag in V, and
mag in V, and ![]() 0.03 mag in B and I, see Sect. 2.2).
0.03 mag in B and I, see Sect. 2.2).
Note that in a preliminary analysis, variables were studied using their differential photometry with respect to a larger number of comparison stars selected in each field (namely four stars per field). However, since results were very much the same in the final study we used just one star per field, namely in each field the star with most accurate magnitude determinations and with colours better matching the RR Lyrae's average colour. This procedure minimize any colour effect on the differential light curves and amplitudes of the variable stars, due to the colour of the comparison stars and the different colour response of the detectors used in the two runs.
Table 3: Coordinates and magnitudes of the comparison stars.
Table 4: V,B,I photometry of the variable stars.
In order to define the periodicities we run GRATIS
on the instrumental differential photometry of the
variable stars. GRATIS performs a period search
according to two different algorithms: (a) the Lomb periodogram (Lomb 1976;
Scargle 1982) and (b) the best-fit of the data with a truncated Fourier series
(Barning 1962). We first performed the
Lomb analysis on a wide period interval. Then the Fourier algorithm was used to
refine the period definition and to find the best fitting model from which to
measure the amplitude and average luminosity of each variable. The period
search employed each of the complete (1999 + 2001) ![]() ,
,
![]() ,
and
,
and ![]() data-sets.
We derived periods and epochs accurate to the third-fourth
decimal place for all the
variable in our sample,
well sampled the B and V light curves
for about 95% of the
RR Lyrae stars, and detected the Blazhko modulation of the light
curve (Blazhko 1907) in about 17% of the RRab's and 5.3% of
the RRc's (see Sect. 5).
Complete coverage of the light variation was also obtained for
4 candidate Anomalous
Cepheids (see Sect. 3.2), for 9 eclipsing binaries with short
orbital period
(P<1.4 days), and for 6 of the Cepheids.
GRATIS also performs a
search for multiple periodicities, and was run on the data of the 10
double-mode variables falling in our two fields, 9 in A97 and 1 newly
discovered. However, our data sampling for these stars is
inadequate to allow
a very accurate derivation of the double-mode periodicities: on this
particular aspect, the very extensive data set collected by MACHO and
OGLE II are clearly
superior to ours.
data-sets.
We derived periods and epochs accurate to the third-fourth
decimal place for all the
variable in our sample,
well sampled the B and V light curves
for about 95% of the
RR Lyrae stars, and detected the Blazhko modulation of the light
curve (Blazhko 1907) in about 17% of the RRab's and 5.3% of
the RRc's (see Sect. 5).
Complete coverage of the light variation was also obtained for
4 candidate Anomalous
Cepheids (see Sect. 3.2), for 9 eclipsing binaries with short
orbital period
(P<1.4 days), and for 6 of the Cepheids.
GRATIS also performs a
search for multiple periodicities, and was run on the data of the 10
double-mode variables falling in our two fields, 9 in A97 and 1 newly
discovered. However, our data sampling for these stars is
inadequate to allow
a very accurate derivation of the double-mode periodicities: on this
particular aspect, the very extensive data set collected by MACHO and
OGLE II are clearly
superior to ours.
Table 5: Informations and average quantities for the variable stars in field A.
Best fitting models of the light variation were computed for all variables with
full light curve coverage, using GRATIS. These models are based on
Fourier series, with the
number of harmonics generally varying from 1 to 5 for the c-type
RR Lyrae's, and from 4 to 12 for the ab-type variables.
Intensity-average differential
![]() ,
,
![]() ,
and
,
and
![]() magnitudes were derived for
all the variables with complete light curves as the integral over the
entire pulsation cycle of the models best fitting the observed data.
By adding the instrumental magnitudes of the reference stars, we obtained the b, v, i mean instrumental magnitudes of the variables, and the mean B, V, I magnitudes in the Johnson-Cousins system
were calculated using the calibration equations given in Sect. 2.2 and the
aperture corrections in Sect. 2.1.
magnitudes were derived for
all the variables with complete light curves as the integral over the
entire pulsation cycle of the models best fitting the observed data.
By adding the instrumental magnitudes of the reference stars, we obtained the b, v, i mean instrumental magnitudes of the variables, and the mean B, V, I magnitudes in the Johnson-Cousins system
were calculated using the calibration equations given in Sect. 2.2 and the
aperture corrections in Sect. 2.1.
Average residuals from the best fitting models for RR Lyrae's with well sampled light curves are 0.02-0.03 mag in V and 0.03-0.04 mag in B for the single-mode, non Blazhko variables, and 0.05-0.10 in V and 0.06-0.12 in Bfor the double-mode stars. The lower accuracy of the B light curves is because the RR Lyrae stars are intrinsically fainter in this passband.
The individual B,V,I photometric measurements of the variables are provided in Table 4. For each star we indicate the star identification number, the field where the star is located, the variable type, Heliocentric Julian Day of observations and corresponding V, B, I magnitudes.
In Tables 5 and 6 (only available in the electronic version) we summarize the main characteristics of the
variables for stars in field A and B, separately. Namely we list: identifier,
coordinates
(![]() and
and ![]() )
at the 2000 equinox, variable star type, period,
heliocentric
Julian day (HJD) of maximum light for the pulsating variables (RR Lyrae's, Cepheids and
)
at the 2000 equinox, variable star type, period,
heliocentric
Julian day (HJD) of maximum light for the pulsating variables (RR Lyrae's, Cepheids and
![]() Scuti) and of the primary (deeper) minimum light for the
eclipsing binaries, number of data-points on the V,B,I light curves,
V,B,I
mean magnitudes and amplitudes of
the light curves, computed as the difference between maximum and
minimum of the best fitting models, for the variable stars with complete
coverage of the light variation. At the bottom of each table we also give
informations on the candidate variables.
The atlas of light curves is presented in the Appendix.
Scuti) and of the primary (deeper) minimum light for the
eclipsing binaries, number of data-points on the V,B,I light curves,
V,B,I
mean magnitudes and amplitudes of
the light curves, computed as the difference between maximum and
minimum of the best fitting models, for the variable stars with complete
coverage of the light variation. At the bottom of each table we also give
informations on the candidate variables.
The atlas of light curves is presented in the Appendix.
The average apparent luminosities of the RR Lyrae stars with full coverage
of the light curve and without shifts between the 1999 and 2001 photometry
are
![]() (
(
![]() ,
67 stars),
,
67 stars),
![]() (
(
![]() ,
67 stars) in field A, and
,
67 stars) in field A, and
![]() (
(
![]() ,
49 stars),
,
49 stars),
![]() (
(
![]() ,
49 stars) in field B.
These values (the V average luminosities in particular)
are fully consistent with those presented in C03. We refer to this
paper for an in-depth discussion of their implications on the distance
to the LMC and related issues.
We also recall that our average luminosities for the field LMC
RR Lyrae stars are in very good agreement with Walker (1992) mean
apparent luminosity of the RR Lyrae stars in the LMC globular clusters
(see Sect. 6 of C03).
,
49 stars) in field B.
These values (the V average luminosities in particular)
are fully consistent with those presented in C03. We refer to this
paper for an in-depth discussion of their implications on the distance
to the LMC and related issues.
We also recall that our average luminosities for the field LMC
RR Lyrae stars are in very good agreement with Walker (1992) mean
apparent luminosity of the RR Lyrae stars in the LMC globular clusters
(see Sect. 6 of C03).
It has often been argued on the better way to compute the
average magnitude of a variable star and on the colour that better
represents the temperature of an RR Lyrae star (Sandage 1990, 1993; Carney et al. 1992; Bono et al. 1995).
The average magnitudes of the variable stars in Tables 5 and 6 were computed
in two different ways, as intensity-averaged means (Cols. 8-10) and
as magnitude-averaged means (Cols. 11-13). Based on theoretical
grounds it has been claimed that large differences may exist between
these two different types of averages, and that for RR Lyrae stars
the difference may be as large as 0.1-0.2 mag in V and B, respectively
(Bono et al. 1995).
In Fig. 12 we plot the differences between the two types of
averages for star in Field A and B separately. Magnitude-averaged mean
magnitudes are generally fainter than the intensity-averaged
mean magnitudes, and the differences increase for fainter magnitudes.
However, they are generally small and only in a few cases exceed
0.1 mag. At the luminosity level of the RR Lyrae stars the average
differences are
![]() ,
,
![]() and
and
![]() for stars in Field A, and
0.022, 0.042, and 0.011 mag for stars in Field B.
for stars in Field A, and
0.022, 0.042, and 0.011 mag for stars in Field B.
Figures 13 and 14 show the position of the various types of variables in the V, B-V CMDs of Field A and B.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{1659f12a.ps}\par\includegraphics[width=8.8cm,clip]{1659f12b.ps}
\end{figure}](/articles/aa/full/2005/05/aa1659/Timg76.gif) |
Figure 12: Differences between magnitude-averaged and intensity-averaged mean magnitudes for the variable stars in field A ( upper panels) and B ( lower panels), separately. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{1659fi13.ps}
\end{figure}](/articles/aa/full/2005/05/aa1659/Timg77.gif) |
Figure 13:
Position of the variable stars on the
V vs. B-V colour-magnitude diagram of field A.
Different symbols are used for the various type of variables
(RR Lyrae stars: filled circles; candidate Anomalous Cepheids: open squares;
blended variables: asterisks; Cepheids:
filled squares; binaries: filled triangles; crosses: |
| Open with DEXTER | |
Variable stars are plotted according to their intensity-averaged magnitudes and colours, and with different symbols corresponding to different types. B,V,I magnitudes and coordinates (in pixels) of all the stars shown in these figures (63 409 in field A and 58 556 in field B) are available in electronic form at CDS.
Our sample contains 5 variables (star #5106, #9578, #9604 and #10320 in Field A, and star #5952 in field B) with periods in the range from 0.29 to 0.63 days, which is typical of RR Lyrae stars, but with V average magnitudes from 0.5 to about 0.9 mag brighter than the average luminosities of the RR Lyrae in the same fields (see open squares and asterisk in Figs. 13 and 14). They also have amplitudes generally smaller than the RR Lyrae of similar period. Average luminosities and amplitudes of these stars are summarized in Table 7 where, in Cols. 7 and 8, we also list the difference in magnitude with respect to the average luminosity of the RR Lyrae stars in the same field (see Sect. 3.1).
These objects could be RR Lyrae variables blended
with stars of comparable
luminosity on the red and blue sides of the horizontal branch (HB) of the old
stellar population in the LMC, namely
clump and/or young main sequence stars. Indeed, star #5952 in field B is considered the blend of an
RR Lyrae and a red giant in MACHO web catalogue
of variable stars (Alcock et al. 2003a, see Sect. 4.2.1).
Table 8 shows schematically how the luminosities and amplitudes of a typical
RR Lyrae in field A (namely the ab-type
RR Lyrae #2525) are expected to change, during the
pulsation cycle, were the star blended to a red giant with
luminosity equal to the average magnitude of the clump stars
in the same field:
![]() ,
and
,
and
![]() mag,
according to C03. The comparison between light curves of resolved and
blended variable is shown in Figure 15.
mag,
according to C03. The comparison between light curves of resolved and
blended variable is shown in Figure 15.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{1659fi14.ps}
\end{figure}](/articles/aa/full/2005/05/aa1659/Timg80.gif) |
Figure 14: Same as Fig. 13 for the variable stars in Field B. |
| Open with DEXTER | |
This exercise shows that as the result of the blend the variable star would
appear about 0.8 and 0.6 mag brighter than
its average V and B luminosities of RR Lyrae star,
its V amplitude would be reduced by
about 50% and the B amplitude by about 37%. These numbers are
very similar to the ![]() and
and ![]() value and amplitudes listed in
Table 7, thus showing that blending is a plausible cause of the
overluminosities of these 5 variable stars.
In order to further investigate the blending hypothesis we checked the
frames.
Stars #9578 and #9604 appear to be rather
isolated. Stars #10320, #5952 and #5106 instead have
faint companions that may occasionally fall within the PSF of the
primary star in bad seeing conditions. This should produce an
increased scatter of the light curves as is indeed the case for star
#5106
which also is
rather blue (B-V=0.119) indicating that this RR Lyrae is likely blended
with a main sequence star. The other
4 objects in Table 7
have instead all rather clean light curves (star #5952 in particular)
and show no shifts between the 1999
and 2001 light curves that might hint they could be unresolved blends in
our 1999 photometry, which was taken in less favourable seeing conditions.
Figure 16 shows the B, V light curves of star #5106 (left panels)
and #10320 (right panels).
The 1999 light curves of #5106 are overluminous, particularly at minimum
light, and have smaller amplitudes
compared to the 2001 ones, as if the star was an unresolved blend in the 1999
photometry, those of star #10320 do not show
any systematic difference between the two datasets.
value and amplitudes listed in
Table 7, thus showing that blending is a plausible cause of the
overluminosities of these 5 variable stars.
In order to further investigate the blending hypothesis we checked the
frames.
Stars #9578 and #9604 appear to be rather
isolated. Stars #10320, #5952 and #5106 instead have
faint companions that may occasionally fall within the PSF of the
primary star in bad seeing conditions. This should produce an
increased scatter of the light curves as is indeed the case for star
#5106
which also is
rather blue (B-V=0.119) indicating that this RR Lyrae is likely blended
with a main sequence star. The other
4 objects in Table 7
have instead all rather clean light curves (star #5952 in particular)
and show no shifts between the 1999
and 2001 light curves that might hint they could be unresolved blends in
our 1999 photometry, which was taken in less favourable seeing conditions.
Figure 16 shows the B, V light curves of star #5106 (left panels)
and #10320 (right panels).
The 1999 light curves of #5106 are overluminous, particularly at minimum
light, and have smaller amplitudes
compared to the 2001 ones, as if the star was an unresolved blend in the 1999
photometry, those of star #10320 do not show
any systematic difference between the two datasets.
For each photometrized object DAOPHOT returns a shape
defining parameter called SHARP, which is related to the intrinsic angular size of the object
image and
measures the regularity and symmetry of the PSF
stellar profile. According to DAOPHOT user manual
objects with values of
![]() are
galaxies and blended doubles, objects with values of
are
galaxies and blended doubles, objects with values of
![]() are
cosmic rays and image defects. In our 2001 photometry stars at the luminosity level of the
HB generally have:
are
cosmic rays and image defects. In our 2001 photometry stars at the luminosity level of the
HB generally have:
![]() .
Average SHARP values
for the 5 overluminous variables
are given in Cols. 9 and 10 of Table 7.
Stars #5952 and #9604 have very good SHARP values, SHARP of
star #9578 is worse but still acceptable.
Star #10320 has negative values of SHARP reflecting the fact that
is at the frame edge
where there are geometric distorsions.
Finally, #5106 has large positive values of SHARP possibly indicating
that the star is double. In conclusion,
star #5106 is likely a blended variable, while
if the other four
stars are actually blends, the two components must be
completely unresolved, so to appear as just one single object
within the PSF profile.
.
Average SHARP values
for the 5 overluminous variables
are given in Cols. 9 and 10 of Table 7.
Stars #5952 and #9604 have very good SHARP values, SHARP of
star #9578 is worse but still acceptable.
Star #10320 has negative values of SHARP reflecting the fact that
is at the frame edge
where there are geometric distorsions.
Finally, #5106 has large positive values of SHARP possibly indicating
that the star is double. In conclusion,
star #5106 is likely a blended variable, while
if the other four
stars are actually blends, the two components must be
completely unresolved, so to appear as just one single object
within the PSF profile.
Table 7: Characteristcs of the 5 variables above the HB.
Tests with artificial stars performed to evaluate the completness of our
photometry in field A show that at the luminosity level of
the RR Lyrae and clump stars (
![]() mag)
our photometry is complete to 96.5%. Since there are 78 RR Lyrae stars
in field A we thus estimate that about 2-3
of this type of variables may be lost
due to incompletness/blending, and, roughly scaling down to the smaller number
of RR Lyrae stars and lower crowding,
less than 2 in field B.
These estimates are reasonably consistent with the number of variables detected
just above the HB in each field.
mag)
our photometry is complete to 96.5%. Since there are 78 RR Lyrae stars
in field A we thus estimate that about 2-3
of this type of variables may be lost
due to incompletness/blending, and, roughly scaling down to the smaller number
of RR Lyrae stars and lower crowding,
less than 2 in field B.
These estimates are reasonably consistent with the number of variables detected
just above the HB in each field.
G04 obtained spectra with FORS1 at the Very Large Telescope (VLT)
and measured
the metallicity of 3 of the overluminous variables.
All of them appear as single
objects in the FORS1 slit.
The derived metallicities are:
![]() for #9604,
for #9604,
![]() for #10320, and
for #10320, and
![]() for #5952,
for an average value of
for #5952,
for an average value of
![]() .
The spectra of these
3 objects are shown in Figs. 9 and 21 of G04, along with those of LMC
RR Lyrae and clump stars, and of Anomalous
Cepheids (ACs) in
.
The spectra of these
3 objects are shown in Figs. 9 and 21 of G04, along with those of LMC
RR Lyrae and clump stars, and of Anomalous
Cepheids (ACs) in ![]() Cen (see G04 Fig. 20), taken with the same
instrumental set-up.
The 3 stars have spectra very similar to the ACs in
Cen (see G04 Fig. 20), taken with the same
instrumental set-up.
The 3 stars have spectra very similar to the ACs in ![]() Cen.
No clear evidence of spectral features due to secondary unresolved
componens are seen, however star #5952
has a prominent G-band similar to that observed
in the spectrum of the clump star shown in Fig. 9 of G04.
Cen.
No clear evidence of spectral features due to secondary unresolved
componens are seen, however star #5952
has a prominent G-band similar to that observed
in the spectrum of the clump star shown in Fig. 9 of G04.
The 5 overluminous variables were observed by MACHO and classified respectively as: ab-type RR Lyrae stars (#5106 and #9604), an RRab blended with a red giant (#5952), and eclipsing binaries (#9578 and 10320; see Table 9). The average V magnitudes of stars #5106 and 5952 agree with ours within 0.05 mag, with our values being systematically fainter. Stars #10320, #9604 and 9578 are instead brighter in our photometry, by 0.14, 0.17 and 0.27 mag, respectively. Nevertheless, even in MACHO photometry they lie above the HB.
Finally, we note that stars #9604 and #10320 were also observed by OGLE II (see Sect. 4.3 and Table 14) and classified ab- and c-type RR Lyrae, respectively. OGLE II average luminosities and light curves of star #9604 agree within 0.1 mag, with our values being slightly brighter (by 0.04 mag in B and 0.11 mag in I, see Table 14). Similarly, OGLE II B data for star #10320 agree within 0.03 mag to our value, being 0.03 mag fainter (we do not have I photometry for this star). However, OGLE II V average luminosities are respectively 0.79 and 0.71 mag fainter than ours, causing these two variables to have rather unlikely colours for RR Lyrae stars: (B-V) 9604=-0.45, (V-I) 9604=1.21 mag, and (B-V) 10320 = -0.17, (V-I) 10320=1.53 mag in OGLE II photometry. Indeed, the OGLE II V light curves of these objects are very poor. No actual V light variation is seen for #10320, possibly indicating a mismatched B,V,I counteridentification.
In conclusion, based on the available observational evidences star #5106 is likely to be the blend of an ab-type RR Lyrae with a young main sequence star. Instead, it is not possible to definitely assign a classification to the other 4 overluminous variables. Sub-arcsec photometry would be needed to shed some light on this issue.
Table 8: Blend of an ab-type RR Lyrae and a clump star in field A.
![\begin{figure}
\par\includegraphics[width=14cm,clip]{1659fi15.ps}
\end{figure}](/articles/aa/full/2005/05/aa1659/Timg111.gif) |
Figure 15: Schematic light curves of a resolved ab-type RR Lyrae star in field A (filled circles) and of its blend with a clump star in the same field (open circles). |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=14cm,clip]{1659fi16.ps}
\end{figure}](/articles/aa/full/2005/05/aa1659/Timg112.gif) |
Figure 16: Light curves of the variable stars #5106 ( left panels) and #10320 ( right panels), open circles and crosses correspond to the 2001 and 1999 data, respectively. |
| Open with DEXTER | |
On the other hand, given the complex stellar population in the LMC, we should also consider whether these 4 objects could be pulsating variables intrinsically brighter that the RR Lyrae stars, such as the Anomalous Cepheids (ACs) commonly found in dwarf Spheroidal galaxies (Pritzl et al. 2002, and references therein), or the low luminosity (LL) Cepheids (Clementini et al. 2003b) and the short period Classical Cepheids (SPCs) found in a number of dwarf Irregular galaxies (Smith et al. 1992; Gallart et al. 1999, 2004; Dolphin et al. 2002).
Anomalous Cepheids are metal-poor (Population II) helium burning stars in the
instability strip, from about 0.5 up to about 2 mag (Bono et al. 1997)
brighter than the
HB of the old stars. They
generally have periods in the range 0.3-2 days, but are too luminous for their
periods to be Population II Cepheids (Wallerstein & Cox 1984).
The high luminosity can be accounted for if
they are more massive than normal old HB stars,
as if they formed from the
coalescence of a close binary (originally a blue straggler), although in some
cases they may result from the evolution of younger, single massive stars. At
low metallicities (
![]() ,
i.e.
,
i.e.
![]() ), a hook in the HB is
predicted, the so called "HB turnover'' (see Caputo 1998, and references
therein), so that stars with masses larger than
), a hook in the HB is
predicted, the so called "HB turnover'' (see Caputo 1998, and references
therein), so that stars with masses larger than ![]()
![]() may cross
the instability strip. Thus, there is a limiting metallicity above
which no Anomalous Cepheid should be generated (Bono et al. 1997;
Marconi et al. 2004). This limit in metallicity should be about
may cross
the instability strip. Thus, there is a limiting metallicity above
which no Anomalous Cepheid should be generated (Bono et al. 1997;
Marconi et al. 2004). This limit in metallicity should be about
![]() for variables around
for variables around ![]()
![]() and
and
![]() for variables around
for variables around ![]()
![]() .
While very common in dwarf Spheroidal
galaxies, Anomalous Cepheids are very rare in globular clusters: only one is
known in the very metal-poor cluster NGC 5466 (Zinn & Dahn 1976;
.
While very common in dwarf Spheroidal
galaxies, Anomalous Cepheids are very rare in globular clusters: only one is
known in the very metal-poor cluster NGC 5466 (Zinn & Dahn 1976;
![]() according to Harris 1996) and two suspected ones are found
in
according to Harris 1996) and two suspected ones are found
in
![]() Cen (Nemec et al. 1994; Kaluzny et al. 1997), a cluster spanning
a wide range in metallicity
(Norris et al. 1996; Suntzeff & Kraft 1996; Pancino et al.
2002) and suspected of being the
remnant of a disrupted dwarf galaxy.
Cen (Nemec et al. 1994; Kaluzny et al. 1997), a cluster spanning
a wide range in metallicity
(Norris et al. 1996; Suntzeff & Kraft 1996; Pancino et al.
2002) and suspected of being the
remnant of a disrupted dwarf galaxy.
Table 9: Counteridentification between MACHO and us for the variable stars in common in field A and B, separately.
The short period Cepheids are blue loop stars, i.e. stars that have ignited the
helium in non degenerate cores (
![]() ), and have periods shorter
than 10 days. They fall on the extension to short periods of the Classical
Cepheids P/L relations (see Smith et al. 1992; Gallart et al. 1999, 2004;
Dolphin et al. 2002).
), and have periods shorter
than 10 days. They fall on the extension to short periods of the Classical
Cepheids P/L relations (see Smith et al. 1992; Gallart et al. 1999, 2004;
Dolphin et al. 2002).
Observed for the first time in NGC 6822 dwarf Irregular galaxy (Clementini et al. 2003b), the LL Cepheids have small amplitudes, luminosities just above the HB, and are fainter and have shorter periods than the short period Cepheids.
It is not possible to decide to which of the above classes these four variables
brighter than the
HB more likely belong, based on
the period-luminosity (P/L) relations, since at their short
periods the P/L relations of Anomalous and Classical Cepheids
merge and are almost indistinguishable. Indeed, in the P/L plane stars #9604,
#5952 and #9578 fall on the extension to short periods of the fundamental mode
Anomalous and Classical Cepheids, while star #10320 lies on the extension to
short periods of the first overtone P/L relations (see Fig. 2 of Baldacci et al. 2004).
Knowledge of the metallicity may allow to break the degeneracy in the
P/L relation, since short period Classical Cepheids and ACs are expected
to have different metallicities, similar to those of their respective Population I
and II parent populations.
Based on the individual and average metallicities G04 conclude
that the three overluminous variables they analyzed would more likely be
ACs with masses
![]() rather than the short period tail of the LMC Classical Cepheids.
Star #9578 lacks a metallicity estimate, hence its possible
classification as AC is more uncertain.
rather than the short period tail of the LMC Classical Cepheids.
Star #9578 lacks a metallicity estimate, hence its possible
classification as AC is more uncertain.
Before going into the details of this comparison
we note that two major differences exist between our, MACHO, and
OGLE II databases:
(i) observing strategy, exposures and time resolution of
our photometric observations were specifically designed to achieve a very
accurate definition of the average luminosity level of the RR Lyrae
stars in the bar of the LMC,
and provide a valuable counterpart to Walker (1992) study of the RR Lyrae
stars in the LMC globular clusters.
RR Lyrae's are instead by-products close to the
limiting magnitude of MACHO and OGLE surveys, whose main target
was the detection of microlensing events in the LMC;
(ii) although we used DoPhot to reduce the 1999 time series, the final
photometry and calibration of our full dataset was handled by
DAOPHOT+ALLFRAME, while both MACHO and OGLE II photometries used
the DoPhot package![]() .
These packages may give similar results when crowding is not too severe;
however DAOPHOT+ALLFRAME
is much more efficient than
DoPhot to resolve and measure faint stellar objects in crowded fields.
This is clearly shown in Fig. 2, where, thanks to ALLFRAME, we reach
about 1-1.5
mag fainter and resolve almost twice the number of stars as with DoPhot.
Moreover,
DoPhot is reported to give systematically
brighter magnitudes for faint stars in crowded regions than DAOPHOT
due to its sky fitting procedure (Alcock et al. 1999, hereinafter A99). These differences
should be kept in mind to
interpret the results of the comparisons discussed
in the next subsections.
.
These packages may give similar results when crowding is not too severe;
however DAOPHOT+ALLFRAME
is much more efficient than
DoPhot to resolve and measure faint stellar objects in crowded fields.
This is clearly shown in Fig. 2, where, thanks to ALLFRAME, we reach
about 1-1.5
mag fainter and resolve almost twice the number of stars as with DoPhot.
Moreover,
DoPhot is reported to give systematically
brighter magnitudes for faint stars in crowded regions than DAOPHOT
due to its sky fitting procedure (Alcock et al. 1999, hereinafter A99). These differences
should be kept in mind to
interpret the results of the comparisons discussed
in the next subsections.
The MACHO collaboration has published calibrated photometry,
namely magnitude-averaged mean magnitudes (Alcock et al. 2003a),
only for the LMC
variable stars.
A99 provide a detailed
description of the photometric
calibration to the Kron-Cousins V and R system of
the twenty top-priority MACHO fields of the LMC which include
fields #6 and #13. They quote an internal precision of
![]() mag (based on 20 000 stars
with
mag (based on 20 000 stars
with ![]() mag) and, from the
comparison
with other published measurements, they estimate a
mean offset between MACHO and all the other data of
mag) and, from the
comparison
with other published measurements, they estimate a
mean offset between MACHO and all the other data of
![]() mag
(see Fig. 7 of their paper).
A99 calibration is referred to as
version 9903018 in following publications of the MACHO team (e.g.
Alcock et al. 2004).
However,
the calibrated average magnitudes
available on MACHO web pages (which, at the time this paper
is being written, correspond to the last update of
April 18th 2002)
are
based on a different
version of A99 photometric calibration (see Alcock et al. 2004).
MACHO catalogue is undoubtedly an invaluable
inventory of the LMC variable star content; however,
because of the non-standard passbands,
the severe "blending''
problems in the fields close to the LMC bar, and the complexity
of the calibration procedures (see A99 for details),
the absolute photometric calibration is a
major concern. As
a matter of fact different versions of the MACHO calibrated
light curves exist,
and it would be very important to know which version most closely
matches the standard system in order to be able to fully exploit
the catalogue.
While working at the
present paper we discussed this issue with
members of the MACHO team who were working on
the
calibration procedures and/or were using the MACHO variable star catalogues (namely Drs. D. Alves, C. Clement,
and G. Kovács).
We exchanged datasets and made comparisons between our
photometry
and data
based on different versions of the MACHO photometric calibrations.
In the following we report results
based on 4 different
datasets of MACHO's photometry,
namely:
mag
(see Fig. 7 of their paper).
A99 calibration is referred to as
version 9903018 in following publications of the MACHO team (e.g.
Alcock et al. 2004).
However,
the calibrated average magnitudes
available on MACHO web pages (which, at the time this paper
is being written, correspond to the last update of
April 18th 2002)
are
based on a different
version of A99 photometric calibration (see Alcock et al. 2004).
MACHO catalogue is undoubtedly an invaluable
inventory of the LMC variable star content; however,
because of the non-standard passbands,
the severe "blending''
problems in the fields close to the LMC bar, and the complexity
of the calibration procedures (see A99 for details),
the absolute photometric calibration is a
major concern. As
a matter of fact different versions of the MACHO calibrated
light curves exist,
and it would be very important to know which version most closely
matches the standard system in order to be able to fully exploit
the catalogue.
While working at the
present paper we discussed this issue with
members of the MACHO team who were working on
the
calibration procedures and/or were using the MACHO variable star catalogues (namely Drs. D. Alves, C. Clement,
and G. Kovács).
We exchanged datasets and made comparisons between our
photometry
and data
based on different versions of the MACHO photometric calibrations.
In the following we report results
based on 4 different
datasets of MACHO's photometry,
namely:
MACHO detected 85
variables in the portion of their field #6 in common with our field A.
We
have counteridentified all of them.
Three of these stars (MACHO numbers: 6.6810.67, 6. 7052.518, and
6.7054.463, corresponding to our stars: #354, 3394 and 17341)
are not found to significantly vary in our photometry.
Other 5 variables classified eclipsing binaries by MACHO, some of which
with very long period (P> 60 day), have
small amplitudes, sometime rather dubious in our photometry.
On the other hand, we have
identified 26 additional variables apparently missed by MACHO;
they
include 18 RR Lyraes (10 RRab's and 8 RRc's), 5 eclipsing binaries,
1 Cepheid, 1 ![]() Scuti, and 1 candidate variable of
unknown type. Thus we have about 34% more short period variables than MACHO in field A.
Scuti, and 1 candidate variable of
unknown type. Thus we have about 34% more short period variables than MACHO in field A.
57 variables have been found by MACHO in the area in common with field B. We have counteridentified 56 of them. The missing object is at the very edge of our field B and its photometry is not reliable. Two of the variables in common, classified by MACHO as eclipsing binaries, have rather small and dubious amplitudes in both photometries. In field B we have identified 13 additional variables that were not detected by MACHO; they include 9 RR Lyraes (3 RRab's and 6 RRc's) and 4 eclipsing binaries. Thus we have about 24% more short period variables than MACHO in field B.
We also noticed that MACHO classification of some of the variable stars in common does not match ours (see Cols. 3 and 4 of Table 9). In particular, there are 6 variables classified as eclipsing binaries by MACHO that we classify as RR Lyrae stars (3) and Cepheids (1 Classical and 2 candidate ACs), 2 RR Lyrae for MACHO that we classify as an eclipsing binary and the blend of an RRab and a main sequence star, and an RR Lyrae + giant branch star for MACHO that we classify as candidate Anomalous Cepheid. Finally we assign a different pulsation mode to 13 other variables, classified as RR Lyrae stars in both photometries.
The comparison between MACHO mean V magnitudes
and our
magnitude-averaged values (see Col. 11 of Tables 5 and 6)
for variables in common with full coverage of the light curve and
without systematic shifts between the 1999 and the 2001 photometries
is shown in Fig. 17, where
filled and open symbols are used for variables in field A
and B, respectively, and triangles mark the double mode RR Lyrae stars.
The average V difference, present photometry minus MACHO, is -0.170 mag
(
![]() ,
66 stars)
in field A, and -0.013 mag (
,
66 stars)
in field A, and -0.013 mag (
![]() ,
44 stars) in field B.
While there is very good agreement for stars in field B, there is a large systematic shift for the
variables in field A, with MACHO web luminosities being on average fainter than ours
by 0.170 mag.
We thus suspect that there may be calibration problems, namely disalignements
and photometric shift between different fields, affecting the individual
average magnitudes published on MACHO web catalogue for the LMC variable stars.
On the other hand we also note that Alcock et al. (2000, hereinafter
A00) median luminosity of
a sub-sample of 680 RRab's in the LMC (
,
44 stars) in field B.
While there is very good agreement for stars in field B, there is a large systematic shift for the
variables in field A, with MACHO web luminosities being on average fainter than ours
by 0.170 mag.
We thus suspect that there may be calibration problems, namely disalignements
and photometric shift between different fields, affecting the individual
average magnitudes published on MACHO web catalogue for the LMC variable stars.
On the other hand we also note that Alcock et al. (2000, hereinafter
A00) median luminosity of
a sub-sample of 680 RRab's in the LMC (
![]() mag)
is in good agreement, within the respective error bars, with the average
luminosity of the RR Lyrae stars in the LMC drawn from the present
photometry (see discussion in Sect. 6 of C03 and their Table 5).
mag)
is in good agreement, within the respective error bars, with the average
luminosity of the RR Lyrae stars in the LMC drawn from the present
photometry (see discussion in Sect. 6 of C03 and their Table 5).
![\begin{figure}
\par\includegraphics[width=8.4cm]{1659fi17.ps}
\end{figure}](/articles/aa/full/2005/05/aa1659/Timg131.gif) |
Figure 17: Comparison between our and MACHO mean V magnitudes for the variable stars in common. Residuals are: this paper - MACHO. Filled and open symbols are used for variable stars in field A and B, respectively. Triangles are the double mode RR Lyrae stars. |
| Open with DEXTER | |
MACHO time series calibrated data for a subsample of 42 variables in common with our photometry (39 RRab, 1 RRc, 1 AC and 1 eclipsing binary, according to our classification; 41 RRab and 1 RRL+GB according to MACHO) were kindly provided to us by Dr. G. Kovács.
This photometry is based on A99 calibration.
The comparison between mean magnitudes
is shown in the top panel of Fig. 18. Individual values are
provided in Table 10,
where we list MACHO's web page magnitude-averaged values (Col. 3), the
present paper magnitude-averaged values (Col. 4), and the
intensity-averaged values from our photometry and Kovács dataset in
Cols. 5 and 6, respectively. Finally, in Cols. 7 and 8 we list the
corresponding residuals this paper minus MACHO web (![]() 1), and this
paper minus Kovács (
1), and this
paper minus Kovács (![]() 2). The agreement with Kovács dataset is
generally good and without apparent offsets between field A and B.
The average difference
2). The agreement with Kovács dataset is
generally good and without apparent offsets between field A and B.
The average difference
![]() is 0.043 mag (
is 0.043 mag (
![]() ,
42 stars), to compare with
,
42 stars), to compare with
![]() mag
(
mag
(
![]() ,
42 stars).
Our average magnitudes are generally fainter than Kovács' as
expected on the basis of the different reduction procedures (see dicussion in Sect. 4.1).
Figure 19 shows the
point-to-point comparison of the light curves of 4 ab-type RR Lyrae
stars (two per each of our fields) representing respectively the best (left
panels) and the worst comparison (right panels) between the two samples. The
two variables shown in the right panels of the figure are systematically
brighter in MACHO photometry.
,
42 stars).
Our average magnitudes are generally fainter than Kovács' as
expected on the basis of the different reduction procedures (see dicussion in Sect. 4.1).
Figure 19 shows the
point-to-point comparison of the light curves of 4 ab-type RR Lyrae
stars (two per each of our fields) representing respectively the best (left
panels) and the worst comparison (right panels) between the two samples. The
two variables shown in the right panels of the figure are systematically
brighter in MACHO photometry.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{1659fi18.ps}
\end{figure}](/articles/aa/full/2005/05/aa1659/Timg137.gif) |
Figure 18: Comparison between our and Kovács ( top panel) and Alves ( bottom panel) mean V magnitudes for the variable stars in common. Residuals are: this paper - others. Filled and open symbols are used for variable stars in field A and B, respectively. |
| Open with DEXTER | |
Alcock et al. (2004) discuss the properties of 330
first-overtone M 5-like RR Lyrae variables contained in 16 LMC MACHO fields
including fields #6 and #13.
These restricted sample includes MACHO "best-fit'' c-type RR Lyrae
with
![]() ,
amplitudes AV> 0.3 and amplitude
ratios in the range
0.75 < AR/AV < 0.85 (C. Clement private
communication; Alcock et al. 2004).
Photometry of these stars is
based on version 9903018 of A99 calibration (Alcock et al. 2004).
Seven of these RRc's are in our sample:
we find that
MACHO's mean magnitudes are on average 0.07 mag brighter than ours
(see Table 12 by Alcock et al. 2004), again
as expected on the basis of the different reduction procedures.
This shift is totally consistent with that found from the larger sample of
newly calibrated MACHO light curves provided us by D. Alves (see following
Sect. 4.2.4),
but at odds with the results from the comparison with the MACHO web values.
We explicitely notice that this is indeed a small sample, since it was
selected as described above, but as discussed in Sect. 4.2.1, and
contrary to what stated by Alves (2004), we have
a much larger number of variable stars in common with MACHO database.
,
amplitudes AV> 0.3 and amplitude
ratios in the range
0.75 < AR/AV < 0.85 (C. Clement private
communication; Alcock et al. 2004).
Photometry of these stars is
based on version 9903018 of A99 calibration (Alcock et al. 2004).
Seven of these RRc's are in our sample:
we find that
MACHO's mean magnitudes are on average 0.07 mag brighter than ours
(see Table 12 by Alcock et al. 2004), again
as expected on the basis of the different reduction procedures.
This shift is totally consistent with that found from the larger sample of
newly calibrated MACHO light curves provided us by D. Alves (see following
Sect. 4.2.4),
but at odds with the results from the comparison with the MACHO web values.
We explicitely notice that this is indeed a small sample, since it was
selected as described above, but as discussed in Sect. 4.2.1, and
contrary to what stated by Alves (2004), we have
a much larger number of variable stars in common with MACHO database.
Dr. D. Alves kindly made available to us time series data for
a subsample of 18 RR Lyrae variables in common with our database (9 for
each field, 10 RRab and 8 RRd
according to our classification; 10 RRab, 4 RRc, 2 RRd, 1 RRe and 1 variable of
unknown type according to MACHO, but classified RRd by A97) along with photometry for the non-variable
stars falling in ![]()
![]() patches
surrounding these RR Lyrae stars.
These photometric data are calibrated
according to A99 and Alcock et al. (2004) calibrations (Alves 2004, private
communication).
Counteridentifications and average magnitudes of these 18 stars
are given in Table 11.
The comparison between
intensity-averaged magnitudes is generally good, (see
Cols. 5 and 6 of Table 11 and bottom panel of Fig. 18), with Alves values being
0.061 mag brighter (
patches
surrounding these RR Lyrae stars.
These photometric data are calibrated
according to A99 and Alcock et al. (2004) calibrations (Alves 2004, private
communication).
Counteridentifications and average magnitudes of these 18 stars
are given in Table 11.
The comparison between
intensity-averaged magnitudes is generally good, (see
Cols. 5 and 6 of Table 11 and bottom panel of Fig. 18), with Alves values being
0.061 mag brighter (
![]() ,
18 stars) than ours and without
significant differences between field A and B.
The corresponding comparison using the magnitude-averaged
luminosities of these RR Lyrae stars available on MACHO
web pages leads to a different result: MACHO web values
are on average 0.067 mag
fainter than ours (see Cols. 3 and 4 of Table 11).
,
18 stars) than ours and without
significant differences between field A and B.
The corresponding comparison using the magnitude-averaged
luminosities of these RR Lyrae stars available on MACHO
web pages leads to a different result: MACHO web values
are on average 0.067 mag
fainter than ours (see Cols. 3 and 4 of Table 11).
Table 10: Comparison with MACHO photometry for the variable stars in common: Kovács subsample.
![\begin{figure}
\par\includegraphics[width=14.8cm,clip]{1659fi19.ps}
\end{figure}](/articles/aa/full/2005/05/aa1659/Timg145.gif) |
Figure 19: Point-to-point comparison of the light curves for ab-type RR Lyrae stars in common with Kovács subsample. Filled dots: our photometry, three arms crosses: MACHO photometry. These represent the best ( left) and worst ( right) cases. |
| Open with DEXTER | |
Table 11: Comparison with MACHO photometry for the variable stars in common: Alves subsample.
The non-variable stars in common were counteridentified by coordinates. They correspond to a total number of 18 996 stars (10 467 in field A, and 8529 in field B, respectively).
Comparison between the two photometries was done dividing
the stars into a bright and a faint sample corresponding respectively
to objects with
V < 18.25 mag (356 stars in field A, and 275 in field B) and objects with
18.25<V<21 mag (4902 stars in field A, and 3969 in field B).
Within each subsample stars where further divided into
magnitude bins 0.25 mag wide.
Average residuals were computed adopting a ![]() rejection
procedure that discarded objects deviating more than 2
rejection
procedure that discarded objects deviating more than 2![]() from the average in the bin.
In Table 12 we list the mean differences
from the average in the bin.
In Table 12 we list the mean differences
![]()
![]() of the stars in the bright subsample (for objects in field A and
B separately),
with their respective
of the stars in the bright subsample (for objects in field A and
B separately),
with their respective ![]() and number of stars per magnitude bin.
Transformation equations between the two photometries were then
computed as the linear
fit of the average residuals of all bins. They are:
and number of stars per magnitude bin.
Transformation equations between the two photometries were then
computed as the linear
fit of the average residuals of all bins. They are:
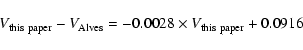
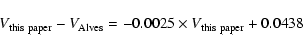
The same comparison done on the stars with
18.25<V<21 mag
is
provided in Table 13 and shown in Fig. 21.
The transformation equations in this magnitude range using
a linear fit with a 2![]() rejection are:
rejection are:
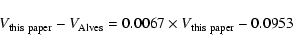
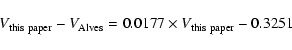
Table 12: Comparison with MACHO photometry for the non-variable stars with V < 18.25, from Alves subsample.
The partial overlap of our field A with
OGLE II field LMC_SC21 (Udalski et al. 2000) gave us the possibility to make a detailed comparison between
the two photometries based on
a large number of stars covering a wide magnitude range.
We have retrieved from the OGLE archive![]() the photometric data corresponding to field LMC_SC21.
The overlapping region
corresponds to 42.25% and 9.84% of our and OGLE II fields, respectively. This
region is located at roughly 5:21:
the photometric data corresponding to field LMC_SC21.
The overlapping region
corresponds to 42.25% and 9.84% of our and OGLE II fields, respectively. This
region is located at roughly 5:21:
![]() :22:38.6
and -70:41:
:22:38.6
and -70:41:
![]() :27:18.4, corresponding
to
1218.95 <X< 2047.44 and
2976.78 <Y< 4967.58 in OGLE II coordinate
system. Inside this area OGLE II has B, V, I photometry for
15 524, 17 067 and 17 582 stars, respectively,
to compare with our 21 524 objects.
Our limiting magnitude is about 1.5 mag fainter
and we resolved about 39, 26, and 22% more stars (in B, V and I, respectively) than OGLE II. Coordinates were aligned to
OGLE II coordinate system and stars in common were counteridentified.
Over the total sample of 14 734 common stars there
are 13 688, 14 483 and 14 734 objects with B, V and Imagnitude in the ranges 12.5-22.7, 12.6-23.1 and 12.3-21.6,
respectively.
Among these objects OGLE II reports 39 variable stars
:27:18.4, corresponding
to
1218.95 <X< 2047.44 and
2976.78 <Y< 4967.58 in OGLE II coordinate
system. Inside this area OGLE II has B, V, I photometry for
15 524, 17 067 and 17 582 stars, respectively,
to compare with our 21 524 objects.
Our limiting magnitude is about 1.5 mag fainter
and we resolved about 39, 26, and 22% more stars (in B, V and I, respectively) than OGLE II. Coordinates were aligned to
OGLE II coordinate system and stars in common were counteridentified.
Over the total sample of 14 734 common stars there
are 13 688, 14 483 and 14 734 objects with B, V and Imagnitude in the ranges 12.5-22.7, 12.6-23.1 and 12.3-21.6,
respectively.
Among these objects OGLE II reports 39 variable stars![]() . We recovered all of them.
Counteridentifications are provided in Table 14
along with average luminosities and classification in types in the two
photometries. There is general agreement in the type classification
and in the derived periods that,
on average, agree within 2-3 decimal digits.
OGLE II classification does not match ours for 4 variable stars, namely
the new candidate RRd, 2 candidate Anomalous Cepheids
and star #5148 that we classify as RRab while is classified RRc by OGLE II. A further object,
star Id
. We recovered all of them.
Counteridentifications are provided in Table 14
along with average luminosities and classification in types in the two
photometries. There is general agreement in the type classification
and in the derived periods that,
on average, agree within 2-3 decimal digits.
OGLE II classification does not match ours for 4 variable stars, namely
the new candidate RRd, 2 candidate Anomalous Cepheids
and star #5148 that we classify as RRab while is classified RRc by OGLE II. A further object,
star Id
![]() is
classified by OGLE II as CepFA; however, OGLE II light curves
for this star are rather poor and the corresponding object in our
photometry (#22592) was not found to vary. Finally,
we have three additional variables in the area in
common that
were apparently missed by OGLE II: an RRc, a binary system, and a
is
classified by OGLE II as CepFA; however, OGLE II light curves
for this star are rather poor and the corresponding object in our
photometry (#22592) was not found to vary. Finally,
we have three additional variables in the area in
common that
were apparently missed by OGLE II: an RRc, a binary system, and a
![]() Scuti star, which are listed at the bottom of Table 14.
For 3 variables (namely stars #9604, 10320, and 25510) there is
a large discrepancy between OGLE II and our V average magnitudes.
Two of these stars (#9604 and 10320) were discussed in Sect. 3.2.
Similarly to them, star #25510 has a very poor V light curve
in OGLE II photometry and an average V magnitude 0.62 mag fainter than ours, leading
to unrealistic
Scuti star, which are listed at the bottom of Table 14.
For 3 variables (namely stars #9604, 10320, and 25510) there is
a large discrepancy between OGLE II and our V average magnitudes.
Two of these stars (#9604 and 10320) were discussed in Sect. 3.2.
Similarly to them, star #25510 has a very poor V light curve
in OGLE II photometry and an average V magnitude 0.62 mag fainter than ours, leading
to unrealistic
![]() and
and
![]() colours for an
RR Lyrae star. We suspect that these 3 stars may have been
wrongly counteridentified in the various photomeric bands.
Figure 22 shows the point-to-point comparison of the V light curves for 3
ab-type
RR Lyrae stars and one Cepheid representing respectively the best
agreement (left panels) and the worst comparison (right panels)
between the two photometries (excluding the 3 above mentioned discrepant
stars).
Large discrepancies are also found among the B magnitudes of
stars #4313 and 8723, that, in the case of the first object, lead in
OGLE II photometry to
a colour
colours for an
RR Lyrae star. We suspect that these 3 stars may have been
wrongly counteridentified in the various photomeric bands.
Figure 22 shows the point-to-point comparison of the V light curves for 3
ab-type
RR Lyrae stars and one Cepheid representing respectively the best
agreement (left panels) and the worst comparison (right panels)
between the two photometries (excluding the 3 above mentioned discrepant
stars).
Large discrepancies are also found among the B magnitudes of
stars #4313 and 8723, that, in the case of the first object, lead in
OGLE II photometry to
a colour
![]() mag rather red for an RR Lyrae star.
mag rather red for an RR Lyrae star.
The comparison between our and OGLE II mean V, B magnitudes
for variable stars in common with
complete light curves and no systematic shifts between our 1999 and 2001
photometry is shown in Fig. 23. Average differences are
![]() mag (
mag (
![]() ,
30 stars discarding stars
#9604, 10320 and 25510, open circles in Fig. 23)
and
,
30 stars discarding stars
#9604, 10320 and 25510, open circles in Fig. 23)
and
![]() mag (
mag (
![]() ,
29 stars, discarding also
star #19711 that does not have B magnitude in OGLE-II), respectively.
These average differences do not
change restricting the comparison only to the RR Lyrae stars.
Our photometry is on average slightly fainter than OGLE-II,
again as expected on the
basis of the different reduction procedures used in the
two photometries (see Sect. 4.1).
The average V magnitude of the RR Lyrae stars in common
using objects with reliable photometry in both
datasets is
,
29 stars, discarding also
star #19711 that does not have B magnitude in OGLE-II), respectively.
These average differences do not
change restricting the comparison only to the RR Lyrae stars.
Our photometry is on average slightly fainter than OGLE-II,
again as expected on the
basis of the different reduction procedures used in the
two photometries (see Sect. 4.1).
The average V magnitude of the RR Lyrae stars in common
using objects with reliable photometry in both
datasets is
![]() mag (
mag (
![]() ,
24 stars)
and
,
24 stars)
and
![]() mag (
mag (
![]() ,
24 stars) in our and
OGLE-II photometry, respectively. These values are in good agreement with
each other and with the average V luminosity of our full sample
of RR Lyrae stars in field A (see end of Sect. 3.1 and C03),
but about 0.06-0.08 mag fainter than
the average V magnitude from the total sample of OGLE II
LMC RRab's:
,
24 stars) in our and
OGLE-II photometry, respectively. These values are in good agreement with
each other and with the average V luminosity of our full sample
of RR Lyrae stars in field A (see end of Sect. 3.1 and C03),
but about 0.06-0.08 mag fainter than
the average V magnitude from the total sample of OGLE II
LMC RRab's:
![]() mag (and
mag (and
![]() mag for the RRc's) by Soszynsky et al. (2003).
Given the small sample of variable stars in common this systematic
shift might appear not very statistically significant, however it is
fully confirmed by the comparison done on the much larger number of
non variable stars at the
same magnitude level (see remaining part of this section and
Table 15).
mag for the RRc's) by Soszynsky et al. (2003).
Given the small sample of variable stars in common this systematic
shift might appear not very statistically significant, however it is
fully confirmed by the comparison done on the much larger number of
non variable stars at the
same magnitude level (see remaining part of this section and
Table 15).
B, V and I residuals between our and OGLE II
photometry for the non variable stars in common are shown in Fig. 24,
while in Fig. 25
we plot the corresponding CMDs (left panels: present paper;
right panels: OGLE II photometry).
Our B, V photometry is generally more accurate and deeper than
OGLE's. Objects falling off the main ridge lines of
OGLE II V, B-V CMD for V> 20.0 and (B-V)<0.2are likely wrong measurements in OGLE II photometry (e.g., blends, wrong
identifications, and wrong counteridentifications between V and B)
since they fall very well on the main branches of our
diagram.
In the I band our photometry appears to be more
uncertain.
However,
the objects that deviate most in our I photometry
(I> 20.0 and
V-I < 0.0)
have magnitudes generally
well below the magnitude level of RR Lyrae and clump stars, that
are the luminosity levels we are mainly interested in.
In order to make a more meaningful comparison of the two photometries we
restricted
the sample of the stars in common only to objects brighter
than V=20.5, B=21.25, and I=20.25 mag.
Average residuals were computed
dividing the objects in magnitude bins and applying an
iterative ![]() -rejection procedure
which discarded objects deviating more than 3
-rejection procedure
which discarded objects deviating more than 3![]() from the average
in the bin.
Results are summarized
in Table 15 (they are based on
5414, 6705, and 7631 stars in V,B,I respectively).
At the magnitude level of RR Lyrae and clump stars (
from the average
in the bin.
Results are summarized
in Table 15 (they are based on
5414, 6705, and 7631 stars in V,B,I respectively).
At the magnitude level of RR Lyrae and clump stars (
![]() ;
and
;
and
![]() ,
respectively) offsets are:
,
respectively) offsets are:
![]() (
(
![]() ),
),
![]() (
(
![]() ),
),
![]() (
(
![]() ), and
), and
![]() (
(
![]() ),
),
![]() (
(
![]() ),
),
![]() (
(
![]() ).
Our photometry is systematically fainter than OGLE II photometry, again as
expected since DoPhot is reported to give systematically
brighter magnitudes for faint stars in crowded regions than DAOPHOT/ALLFRAME,
and since we resolve many more faint stars than OGLE II in the area
in common.
Transformation equations between the two photometries
were then computed as linear fits of the average
residuals of all the bins:
).
Our photometry is systematically fainter than OGLE II photometry, again as
expected since DoPhot is reported to give systematically
brighter magnitudes for faint stars in crowded regions than DAOPHOT/ALLFRAME,
and since we resolve many more faint stars than OGLE II in the area
in common.
Transformation equations between the two photometries
were then computed as linear fits of the average
residuals of all the bins:
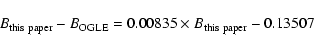
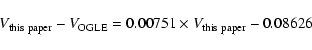
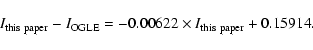
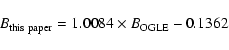
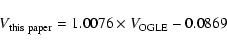
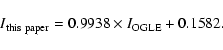
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{1659fi20.ps}
\end{figure}](/articles/aa/full/2005/05/aa1659/Timg188.gif) |
Figure 20: Comparison with MACHO photometry (Alves subsample) for non-variable stars brighter than 18.25 mag. Residuals are this paper minus MACHO. Lines indicate the linear fits of the average residuals of all bins. |
| Open with DEXTER | |
Table 13: Comparison with MACHO photometry for the non-variable stars with 18.25<V<21, from Alves subsample.
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{1659fi21.ps}
\end{figure}](/articles/aa/full/2005/05/aa1659/Timg189.gif) |
Figure 21: Same as Fig. 20 for non-variable with 18.25 <V< 21 mag. |
| Open with DEXTER | |
Figure 26 shows the period distribution of the single-mode RR Lyrae's
(125 objects). The two peaks correspond to the average period of the c- and ab-type
pulsators, respectively:
![]() days (
days (
![]() ,
38 stars) and
,
38 stars) and
![]() days (
days (
![]() ,
87 stars),
to compare with 0.342 and 0.583 day of A96, and with 0.339 and 0.573 days by
Soszynsky et al. (2003).
Our average periods are in good agreement with both A96 and Soszynsky et al.
(2003) results, which are based on much larger samples, and confirm
that the average period of the ab-type variables of the LMC
is intermediate
between the periods of the Galactic RR Lyrae stars of
Oosterhoff type I (OoI) and II (OoII),
but it is actually closer to the Oo I clusters (being
,
87 stars),
to compare with 0.342 and 0.583 day of A96, and with 0.339 and 0.573 days by
Soszynsky et al. (2003).
Our average periods are in good agreement with both A96 and Soszynsky et al.
(2003) results, which are based on much larger samples, and confirm
that the average period of the ab-type variables of the LMC
is intermediate
between the periods of the Galactic RR Lyrae stars of
Oosterhoff type I (OoI) and II (OoII),
but it is actually closer to the Oo I clusters (being
![]() ,
and 0.65 days in Oo I and II
clusters, respectively; Oosterhoff 1939).
Our results also indicate that
the average pulsation properties of the RR Lyrae stars in the two fields
are slightly different, with variables in field B being more definitely of Oo
type I. Field B contains in fact a larger number of ab-type RR Lyrae with
periods around half a day
(10 out of 35 RRab's in field B have
,
and 0.65 days in Oo I and II
clusters, respectively; Oosterhoff 1939).
Our results also indicate that
the average pulsation properties of the RR Lyrae stars in the two fields
are slightly different, with variables in field B being more definitely of Oo
type I. Field B contains in fact a larger number of ab-type RR Lyrae with
periods around half a day
(10 out of 35 RRab's in field B have
![]() days corresponding
to 28.6%, while only 5 out of 52 in field A, corresponding to 9.6%), as confirmed by the average periods computed keeping
the variables in the two fields separate. These are:
days corresponding
to 28.6%, while only 5 out of 52 in field A, corresponding to 9.6%), as confirmed by the average periods computed keeping
the variables in the two fields separate. These are:
![]() days (
days (
![]() ,
20 stars),
,
20 stars),
![]() days (
days (
![]() ,
52 stars), and
,
52 stars), and
![]() days (
days (
![]() ,
18 stars),
,
18 stars),
![]() days (
days (
![]() ,
35 stars),
in field A and B, respectively.
,
35 stars),
in field A and B, respectively.
Table 14: Variable stars inside the area in common with OGLE II field LMC_SC21.
![\begin{figure}
\par\includegraphics[width=14.6cm,clip]{1659fi22.ps} %\end{figure}](/articles/aa/full/2005/05/aa1659/Timg207.gif) |
Figure 22: Point-to-point comparison of the V light curves for 3 ab-type RR Lyrae stars and a Classical Cepheid ( lower right panel) in common with OGLE II. Filled dots: our photometry, three arms crosses: OGLE II photometry. As in Fig. 19, these represent the best ( left) and worst ( right) cases. |
| Open with DEXTER | |
The B and V amplitudes (AB, AV, see Cols. 14 and 15 of
Tables 5 and 6)
were used together with the newly derived periods to build the period-amplitude
diagrams shown in Fig. 27. The overlap in the transition region
between ab and c-type RR Lyrae is small (5 objects, see Fig. 26).
Our shortest period ab-type RR Lyrae's are:
star #19450 in field A, P=0.398 days, AV=1.344 and
AB=1.709 mag; and star #19037 in field B, P=0.411 days,
AV=1.466 and AB=1.821 mag. The longest period c-types
are: star #6415 in
field A, with P=0.443 days,
AV=0.438 and AB=0.473 mag, and stars #6957 and #7064 in field B,
respectively with P=0.406 days, AV=0.396, AB=0.568 mag and
P=0.401 days, AV=0.474, AB=0.607 mag.
These stars define the transition region between ab and c-type RR Lyrae stars that, in our sample, occurs at
![]() days, (
days, (
![]() days in A96).
They are labelled in the period-amplitude distributions in
Fig. 27.
days in A96).
They are labelled in the period-amplitude distributions in
Fig. 27.
A96 discuss at some length the existence in their period and amplitude
distributions (see Figs. 1 and 6 of A96) of an extra-large number of
variables with period around 0.28 days,
which have asymmetric light curves, but low amplitudes. A96
classify these variables as possible
second-overtone RR Lyrae's (type e), and see also the
discussion in Soszynsky et al. (2003).
Figure 26 does not show clear evidence for an extra peak
around ![]() days. We have 8 objects in the
period range from 0.265 to 0.291 days (4 in each of the two fields). Only two of them show
asymmetric light curves, namely:
star #2223 in field A with P=0.288 days,
AV=0.493 mag, AB=0.604 mag, and AI=0.499 mag;
and star #10585 in field B with P=0.270 days, AV=0.478 mag, and
AB=0.657 mag.
Another RRc of slightly longer period has very asymmetric curves:
star #7490 in field B with P=0.305 days,
AV=0.505 and AB=0.637.
days. We have 8 objects in the
period range from 0.265 to 0.291 days (4 in each of the two fields). Only two of them show
asymmetric light curves, namely:
star #2223 in field A with P=0.288 days,
AV=0.493 mag, AB=0.604 mag, and AI=0.499 mag;
and star #10585 in field B with P=0.270 days, AV=0.478 mag, and
AB=0.657 mag.
Another RRc of slightly longer period has very asymmetric curves:
star #7490 in field B with P=0.305 days,
AV=0.505 and AB=0.637.
The
![]() ,
,
![]() distributions of the
variables in the two
fields are similar (see Fig. 27),
and resemble Fig. 6 of A96,
however our AV amplitudes range is slightly larger than in A96, with AV values from 0.29 to 1.47 mag in our sample to compare with
0.35-1.35 in A96.
distributions of the
variables in the two
fields are similar (see Fig. 27),
and resemble Fig. 6 of A96,
however our AV amplitudes range is slightly larger than in A96, with AV values from 0.29 to 1.47 mag in our sample to compare with
0.35-1.35 in A96.
The period - amplitude distributions of the LMC variables were
compared with the relations defined by the
ab-type RR Lyrae's in the globular clusters M 3, M 15 and ![]() Cen,
shown by lines in Fig. 27.
Solid lines were derived from the photometry of
Carretta et al. (1998) for M 3, and Bingham
et al. (1984) for M 15, and were computed
as follow: we first derived the
period-amplitude relations using the M 3 sample which is more extended; then
we shifted the intercept of these relations while holding fixed the
slopes, until a good fit (by eye) was obtained also for the variables in
M 15, which are too few in number to give a satisfactory best fit by
themselves. Dashed lines in the lower panels of Fig. 27 are the
Cen,
shown by lines in Fig. 27.
Solid lines were derived from the photometry of
Carretta et al. (1998) for M 3, and Bingham
et al. (1984) for M 15, and were computed
as follow: we first derived the
period-amplitude relations using the M 3 sample which is more extended; then
we shifted the intercept of these relations while holding fixed the
slopes, until a good fit (by eye) was obtained also for the variables in
M 15, which are too few in number to give a satisfactory best fit by
themselves. Dashed lines in the lower panels of Fig. 27 are the
![]() relations
derived for M 3 and
relations
derived for M 3 and ![]() Cen by
Clement (2000) using only RRab's with regular light curves
(see also Clement & Shelton 1999; and Clement & Rowe 2000).
Cen by
Clement (2000) using only RRab's with regular light curves
(see also Clement & Shelton 1999; and Clement & Rowe 2000).
RR Lyrae's in field B seem to better follow the amplitude-period relations of the variables in M 3 and, as already noted, to belong to the OoI type. Variables in field A, instead, have pulsation properties more intermediate between the two Ooostheroff types.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{1659fi23.ps}
\end{figure}](/articles/aa/full/2005/05/aa1659/Timg214.gif) |
Figure 23: Comparison between our and Ogle II mean V and B magnitudes for the variable stars in common. Residuals are: this paper - OGLE II. Open symbols are used for the most deviating stars (see text). |
| Open with DEXTER | |
The average luminosity we derive from the 10 RRd's in our sample,
using the magnitude-averaged values in Col. 11 of Tables 5 and 6
(
![]() ,
,
![]() ,
10 stars) is
in very good
agreement with A00 average luminosity of the
LMC double mode RR Lyrae stars (
,
10 stars) is
in very good
agreement with A00 average luminosity of the
LMC double mode RR Lyrae stars (
![]() ).
).
We may compare the average luminosity of the RRd variables with the average
luminosity of the single-mode RR Lyrae stars in our two fields. Due to the difference in
reddening between the two fields (see C03) this comparison is better done keeping the
variables in the two areas separated.
We found
![]() (
(
![]() ), and
), and
![]() (
(
![]() )
from the
average of the 6 RRd's in field A,
to compare with
average values derived from the single-mode pulsators
of
)
from the
average of the 6 RRd's in field A,
to compare with
average values derived from the single-mode pulsators
of
![]() (
(
![]() ,
61 stars), and
,
61 stars), and
![]() (
(
![]() ,
61 stars), respectively;
and
,
61 stars), respectively;
and
![]() (
(
![]() )
and
)
and
![]() (
(
![]() )
from the
average of the 4 RRd's in field B,
to compare with
average values derived from the single-mode pulsators
of
)
from the
average of the 4 RRd's in field B,
to compare with
average values derived from the single-mode pulsators
of
![]() (
(
![]() ,
45 stars), and
,
45 stars), and
![]() (
(
![]() ,
45 stars), respectively.
The RRd pulsators seem to be slightly brighter than
the single-mode ones
in the same field (by 0.043 mag in V and 0.093 in B in field A, and by 0.097 in V and 0.109
in B in field B), although the statistical significance of this result
might be weak given the rather small number of objects. A similar conclusion was also
reached by G04.
,
45 stars), respectively.
The RRd pulsators seem to be slightly brighter than
the single-mode ones
in the same field (by 0.043 mag in V and 0.093 in B in field A, and by 0.097 in V and 0.109
in B in field B), although the statistical significance of this result
might be weak given the rather small number of objects. A similar conclusion was also
reached by G04.
Table 15:
Comparison of our and OGLE II photometry for the non variable
stars in common.
![]() ,
,
![]() ,
,
![]() are: this
paper - OGLE II.
are: this
paper - OGLE II.
In recent years Jurcsik & Kovács (1996, hereinafter JK96), Kovács & Jurcsik (1996, 1997, hereinafter KJ96, KJ97), and Kovács & Walker (2001, hereinafter KW01) have derived empirical relations between the parameters of the Fourier decomposition of the V light curves of the fundamental mode RR Lyrae stars and their basic stellar quantities, namely: intrinsic magnitude and colours, effective temperature, gravity and metal abundance. These relationships were calibrated on Galactic field RR Lyrae (JK96) and on globular clusters variables (KJ96; KJ97; and KW01), and should allow to derive the physical parameters for any RRab provided that accurate Fourier parameters of V light curve are available.
Our sample of ab-type LMC RR Lyrae stars with high quality multiband light curves, metal abundances homogeneously derived and covering more than 1 dex metallicity range (G04), all at the same distance from us, and with reddening consistently derived (C03), may be used to check these empirical relationships.
JK96 show that the
light curves of the variable stars
must satisfy completeness and regularity criteria, referred to by the
authors as compatibility conditions,
for the Fourier parameters to predict reliable empirical quantities.
Namely, the deviations of the Fourier parameters
should not exceed the
maximum value (![]() )
of 3, with
maximum deviations
)
of 3, with
maximum deviations
![]() possibly
indicating that incompatibility with the empirical predictions can
be expected (Kovács & Kanbur 1998, hereinafter KK98).
The deviation parameters DF are defined as
DF =
possibly
indicating that incompatibility with the empirical predictions can
be expected (Kovács & Kanbur 1998, hereinafter KK98).
The deviation parameters DF are defined as
DF =
![]() ,
where
,
where
![]() ,
,
![]() are respectively the observed value of a given
Fourier parameter and its predicted value from the other observed
parameters, and
are respectively the observed value of a given
Fourier parameter and its predicted value from the other observed
parameters, and ![]() is the respective standard deviation
(see Eq. (6) and Table 6 of JK96).
JK96 find that Blazhko stars
do not generally satisfy the compatibility conditions.
However, Cacciari et al. (2004), in their extensive analysis of
the RR Lyrae stars in the globular cluster M 3, based
on the large database of Corwin & Carney (2001),
found that 40% of the
variables with
is the respective standard deviation
(see Eq. (6) and Table 6 of JK96).
JK96 find that Blazhko stars
do not generally satisfy the compatibility conditions.
However, Cacciari et al. (2004), in their extensive analysis of
the RR Lyrae stars in the globular cluster M 3, based
on the large database of Corwin & Carney (2001),
found that 40% of the
variables with
![]() were indeed Blazhko stars.
were indeed Blazhko stars.
![\begin{figure}
\par\includegraphics[width=8.3cm,clip]{1659fi24.ps}
\end{figure}](/articles/aa/full/2005/05/aa1659/Timg244.gif) |
Figure 24: Comparison between our and OGLE II photometry for the about 14 000 stars in common. Residuals are this paper minus OGLE II. |
| Open with DEXTER | |
From our sample of 87 LMC RRab's we thus chose objects with fully
covered V
light curves, no systematic shifts between 1999 and 2001 photometry,
and not affected (or suspected to be affected) by Blazhko effect.
The selected variables were then tested against JK96
compatibility conditions; 29 of them passed the test.
This sample includes 14 stars with
![]() ,
and
15 objects with
,
and
15 objects with
![]() ,
(
,
(
![]() can
still provide acceptable results, cf. Cacciari et al. 2004).
Parameters from the Fourier decomposition of their V light curves
are provided in Table 16, while in Col. 3 of Table 17
we report the highest maximum
can
still provide acceptable results, cf. Cacciari et al. 2004).
Parameters from the Fourier decomposition of their V light curves
are provided in Table 16, while in Col. 3 of Table 17
we report the highest maximum ![]() value of each star.
Metallicities ([Fe/H]), absolute magnitudes (MV), intrinsic (B-V)0
colours, and effectived temperatures (
value of each star.
Metallicities ([Fe/H]), absolute magnitudes (MV), intrinsic (B-V)0
colours, and effectived temperatures (
![]() ),
were then computed from these parameters
using the relationships by
JK96, KW01 and Kovács (2002, hereinafter K02).
They are provided in Cols. 4, 6, 8, and 10 of Table 17.
),
were then computed from these parameters
using the relationships by
JK96, KW01 and Kovács (2002, hereinafter K02).
They are provided in Cols. 4, 6, 8, and 10 of Table 17.
These values were compared with the corresponding observed quantities
obtained in the present photometric study and in G04 spectroscopic
analysis. These comparisons are described in detail
in the following sections.
![\begin{figure}
\par\includegraphics[width=8.1cm,clip]{1659fi25.ps}
\end{figure}](/articles/aa/full/2005/05/aa1659/Timg249.gif) |
Figure 25:
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7.6cm,clip]{1659fi26.ps}
\end{figure}](/articles/aa/full/2005/05/aa1659/Timg250.gif) |
Figure 26: Number vs. Period histogram of the single-mode RR Lyrae variables in our sample (125 objects). |
| Open with DEXTER | |
The average difference between photometric and spectroscopic metallicities
is
![]() dex, with the photometric abundances being larger
as expected.
In the left panel of Fig. 28 we show the run of the
dex, with the photometric abundances being larger
as expected.
In the left panel of Fig. 28 we show the run of the ![]() 31 values with
G04 metal abundances,
and in the righ panel the star-to-star comparison between photometric
and G04 spectroscopic metallicities for these 22 stars.
31 values with
G04 metal abundances,
and in the righ panel the star-to-star comparison between photometric
and G04 spectroscopic metallicities for these 22 stars.
The correlations in both panels are not very strong, though, admittedly, some
of the most deviating objects have large ![]() values.
values.
![\begin{figure}
\par\includegraphics[width=12cm,clip]{1659fi27.ps}
\end{figure}](/articles/aa/full/2005/05/aa1659/Timg257.gif) |
Figure 27:
|
| Open with DEXTER | |
Table 16: Fourier parameters of the light curves and corresponding estimate of the star metallicity, absolute magnitude, intrinsic (B-V)0 colour, and effective temperature.
Table 17: Metallicities, absolute magnitudes, (B-V)0 colours, and effective temperatures from the Fourier parameters of the light curves for the subset of 29 RRab stars.
![\begin{figure}
\par\includegraphics[width=15cm,clip]{1659fi28.ps}
\end{figure}](/articles/aa/full/2005/05/aa1659/Timg320.gif) |
Figure 28:
Left panel: run of the |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=15cm,clip]{1659fi29.ps}
\end{figure}](/articles/aa/full/2005/05/aa1659/Timg321.gif) |
Figure 29:
Star-to-star comparison between MV values ( left panel) and
(B-V)0 colours ( right panel)
derived from the Fourier parameters of the light curves and the
corresponding observed quantities. For ease of comparison
we show the 1:1 lines.
Filled and open symbols mark variables with
|
| Open with DEXTER | |
In conclusion, the comparison between empirical determinations from the
Fourier parameters of the light curves and corresponding observed
quantities for the 29 ab-type RR Lyrae stars in the LMC has
revealed a number of discrepancies, in particular
between the derived and observed MV and (B-V)0 values, deserving
deeper investigation based on larger samples of stars than available here.
In this respect, we notice that similar discrepancies in
the MV and (B-V)0 values have been found by Cacciari et al. (2004),
from the analysis of the RR Lyrae stars in M 3, and in the MV values
of the variables in ![]() Cen (Clement & Rowe 2000) and M 15 (Kaluzny et al. 2000).
Cen (Clement & Rowe 2000) and M 15 (Kaluzny et al. 2000).
Acknowledgements
We are indebted to G. Rodighiero for her advice on the use of SExtractor, to M. Bellazzini and M. Messineo for their help in setting the DoPHOT reductions, and to R. Merighi for help in the layout of some of the figures of the paper. It is a pleasure to thank D. Alves, C. Clement and G. Kovács for providing some of the data on which the comparison with MACHO photometry is based. Special thanks go to C. Cacciari for many valuable discussions on the parameters of the Fourier decomposition of the light curves, and for lending us her macros to compute the basic stellar quantities from the Fourier parameters. We thank the anonymous referee for useful suggestions.
This paper utilizes public domain data obtained by the MACHO Project, jointly funded by the US Department of Energy through the University of California, Lawrence Livermore National Laboratory under contract No. W-7405-Eng-48, by the National Science Foundation through the Center for Particle Astrophysics of the University of California under cooperative agreement AST-8809616, and by the Mount Stromlo and Siding Spring Observatory, part of the Australian National University.
This work was partially supported by MIUR - Cofin98 under the project "Stellar Evolution'', by MIUR - Cofin00 under the project "Stellar observables of cosmological relevance'', and by MIUR - Cofin02 under the project "Stellar populations, distances and star formation histories in Local Group galaxies of all morphological types''.
The Atlas of the light curves for the 162 short period variables stars in our two LMC fields is available in electronic form. A portion is shown here (Fig. A.1).
The photometric data
are folded with the ephemerides given
in Table 5 and 6.
Variables stars are divided
per field and grouped by type: RR Lyrae stars (ab-, c-, d-type
separately), ![]() Scuti, candidate Anomalous Cepheids, Cepheids, eclipsing
binaries, and within each
group are ordered by increasing period.
Scuti, candidate Anomalous Cepheids, Cepheids, eclipsing
binaries, and within each
group are ordered by increasing period.
![\begin{figure}
\par\includegraphics[width=17.6cm]{1659A1_1.ps}\end{figure}](/articles/aa/full/2005/05/aa1659/Timg328.gif) |
Figure A.1: B,V,I light curves of the ab-type RR Lyrae stars in field A, variables are ordered by increasing period. Open and filled symbols are used for the 1999 and 2001 data, respectively. |
![\begin{figure}
\par\includegraphics[width=17.6cm]{1659A2_1.ps}\end{figure}](/articles/aa/full/2005/05/aa1659/Timg334.gif) |
Figure A.2: B,V,I light curves of the c-type RR Lyrae stars in field A, variables are ordered by increasing period. Open and filled symbols are used for the 1999 and 2001 data, respectively. |
![\begin{figure}
\par\includegraphics[width=17.6cm,clip]{1659A4.ps}\end{figure}](/articles/aa/full/2005/05/aa1659/Timg337.gif) |
Figure A.4: B,V,I light curves of Classical Cepheids in field A, variables are ordered by increasing period. Open and filled symbols are used for the 1999 and 2001 data, respectively. |
![\begin{figure}
\par\includegraphics[width=17.6cm,clip]{1659A6_1.ps}\end{figure}](/articles/aa/full/2005/05/aa1659/Timg339.gif) |
Figure A.6: B,V,I light curves of the ab-type RR Lyrae stars in field B, variables are ordered by increasing period. Open and filled symbols are used for the 1999 and 2001 data, respectively. |
![\begin{figure}
\par\includegraphics[width=17.6cm,clip]{1659A7_1.ps}\end{figure}](/articles/aa/full/2005/05/aa1659/Timg343.gif) |
Figure A.7: B,V,I light curves of the c-type RR Lyrae stars in field B, variables are ordered by increasing period. Open and filled symbols are used for the 1999 and 2001 data, respectively. |
![\begin{figure}
\par\includegraphics[width=17.6cm,clip]{1659A9.ps}\end{figure}](/articles/aa/full/2005/05/aa1659/Timg346.gif) |
Figure A.9: B,V,I light curves of binaries in field B, variables are ordered by increasing period. Open and filled symbols are used for the 1999 and 2001 data, respectively. |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{1659fig3.ps}
\end{figure}](/articles/aa/full/2005/05/aa1659/Timg347.gif) |
Figure 3:
LMC sub-field A1 (
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{1659fig4.ps}
\end{figure}](/articles/aa/full/2005/05/aa1659/Timg348.gif) |
Figure 4:
FORS1 LMC sub-field A4 (
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{1659fig5.ps}
\end{figure}](/articles/aa/full/2005/05/aa1659/Timg349.gif) |
Figure 5:
FORS1 LMC sub-field A2 (
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{1659fig6.ps}
\end{figure}](/articles/aa/full/2005/05/aa1659/Timg350.gif) |
Figure 6:
FORS1 LMC sub-field A3 (
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{1659fig7.ps}
\end{figure}](/articles/aa/full/2005/05/aa1659/Timg351.gif) |
Figure 7:
FORS1 LMC sub-field B1 (
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{1659fig8.ps}
\end{figure}](/articles/aa/full/2005/05/aa1659/Timg352.gif) |
Figure 8:
FORS1 LMC sub-field B4 (
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{1659fig9.ps}
\par\end{figure}](/articles/aa/full/2005/05/aa1659/Timg353.gif) |
Figure 9:
FORS1 LMC sub-field B2 (
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{1659fi10.ps}
\end{figure}](/articles/aa/full/2005/05/aa1659/Timg354.gif) |
Figure 10:
FORS1 LMC sub-field B3 (
|
| Open with DEXTER | |
| |
Figure 11:
Left panel: finding chart of the ab-type RR Lyrae star #3805, which is
located slightly outside
sub-field A4 in the East direction.
Right panel: finding chart of the c-type RR Lyrae star #1387, which is located slightly
outside sub-field B4 in the South/East direction.
Both maps show a
40 |
| Open with DEXTER | |
Table 6: Informations and average quantities for the variable stars in field B.
Table 5: Informations and average quantities for the variable stars in field A.
Table 9: Counteridentification between MACHO and us for the variable stars in common in field A and B, separately.
Table 14: Variable stars inside the area in common with OGLE II field LMC_SC21.
Table 16: Fourier parameters of the light curves and corresponding estimate of the star metallicity, absolute magnitude, intrinsic (B-V)0 colour, and effective temperature.