A&A 427, 371-376 (2004)
DOI: 10.1051/0004-6361:20041271
V. Lainey1,2 - J. E. Arlot2 - A. Vienne2,3
1 - Royal Observatory of Belgium, Ringlaan 3, 1180 Brussels, Belgium
2 -
Institut de mécanique céleste et de calcul
des éphémérides - Observatoire de Paris, UMR 8028 du CNRS,
77 avenue Denfert-Rochereau, 75014 Paris, France
3 -
Université Lille 1, IMCCE/LAL, 1 impasse de l'Observatoire, 59000
Lille, France
Received 11 May 2004 / Accepted 5 July 2004
Abstract
We present a new model of the four Galilean satellites Io, Europa, Ganymede and Callisto, able to deliver accurate
ephemerides over a very long time span (several centuries). In the first paper (Lainey et al. 2004, A&A, 420, 1171) we gave
the equations of the dynamical model. Here we present the fit of this model to the observations, covering more
than one century starting from 1891. Our ephemerides, based on this first fit called L1, are available on the
web page of the IMCCE at the URL http://www.imcce.fr/ephemeride_eng.html.
Key words: astrometry - planets and satellites: individual: Io - planets and satellites: individual: Europa - planets and satellites individual: Ganymede - planets and satellites: individual: Callisto - ephemerides
The problem of the motion of the Galilean satellites of Jupiter is one of the most interesting, but difficult, problems of the dynamics of the Solar system. The Galilean satellites behave like a miniature solar system and combine gravitational and non-gravitational effects, such as mutual perturbations, perturbations by the Sun, the shape of Jupiter, the planet Saturn, tidal effects, relativistic effects, etc. Therefore, obtaining very accurate ephemerides has been one of the prime tasks of generations of astronomers over many centuries (Laplace, Damoiseau, Sampson, De Sitter, Lieske, Ferraz-Mello, Sagnier, Vu, etc.). Moreover, the Galilean satellites were also a goal of the space probes and new problems arose when the strong tidal effects of Jupiter, mainly on Io, were discovered. The measurement of orbital acceleration induced by these tidal effects may lead to a better modeling of the interior of the satellites. This indicates the interest in having a very accurate model of the motion of these bodies and to be able to compare accurate observations to ephemerides in order to evaluate known but not quantified effects. For that purpose, we built a new dynamical model based on a new numerical integration (Lainey et al., Paper I). In the present paper, we fit this model to the most precise observations made from 1891 to 2003.
Table 1: Observations used in L1 fit.
The observations used in the fit extend from 1891 to 2003. Their accuracy is unequalled in the instruments used and the epoch when the observations were done. In this paper, the number of observations refers to the amount of time that a satellite has been observed (e.g. a photographic plate containing three satellites will count for three observations). Note that we did not use eclipse observations by Jupiter because of the bad astrometric accuracy of these data due to the atmosphere of Jupiter. Table 1 summarizes the observations used in our ephemerides.
These observations have various origins and were made with various instruments. The observations between 1891 and 1910 were made in Helsingfors (Finland) and at Pulkovo observatory (f=3.4 m) in Russia. Those between 1917 and 1918 were done by Chevalier in China (f=7.1 m). The de Sitter's observations were done in 1918-1919 at Greenwich and in 1924 at the Cape (f=6.9 m). Finally, observations done in 1934 and 1936 were done respectively in Bucharest (f=6.1 m) and Paris (f=3.4 m).
The whole set of these observations was already used in a fit of the Sampson-Lieske model (Lieske 1977), providing the G5 ephemerides (Arlot 1982a). They have been published in a B1950 equatorial frame in Arlot (1982b).
The observation of the mutual events (also called mutual phenomena: eclipses and occultations that involve two satellites, but not Jupiter) of the Galilean satellites started in 1973, leading to the creation of the PHEMU campaigns taking place every six years. The observation of these phenomena are regularly performed in many observatories throughout the world. As this kind of observation is photometric, the reduction method is quite different from the astrometrical one. We note that the absence of an atmosphere on the Galilean satellites and the fact that these measurements are timings lead to very accurate data. Aksnes & Franklin (1976) developed a reduction method for this kind of observation. Hence, we used the values based on this method later published in Franklin et al. (1984), Franklin (1991), Kaas et al. (1999) and corrected by the "DT'' values following Kaas et al. (1999).
These observations were obtained with an automatic transit telescope at Flagstaff (USA). An observational program of 17 natural satellites of Jupiter and Neptune called FASTT (Flagstaff Astrometric Scanning Transit Telescope) started in 1998 (Stone & Harris 2000, 2000, 2001). A set of observations covering the time span 2001-2003, as yet unpublished, has been kindly communicated to us by Dr. Stone.
We performed an adjustment to our numerical model presented in Paper I, to all the observations from the previous section.
This adjustment was required to take into account several corrections in the shift from the reference frame (in time and space) of
the observations to the reference frame of the numerical integrator. Hence, in order to
calculate the theoretical positions corresponding to the
observations, the change of time scale from UT/UTC (depending on the epoch of
the observations) to ET/TT, and the light time correction have been applied to each observation. This final calculation is carried out by iterations using the equality
As was indicated by Noyelles et al. (2003), there is a subtlety in the particular case of mutual eclipses. In such a configuration, the light time to the eclipsing satellite should be replaced by the light time to the eclipsed satellite minus the light time necessary to cross the eclipsing-eclipsed satellite distance. This modification comes from the fact that the observed event introduces only the eclipsed satellite, the eclipsing satellite not being present in the previous case. At the time when the eclipsed satellite enters the penumbra, the eclipsing satellite has already moved by the light time corresponding to the eclipsing-eclipsed satellite distance.
The aberration has been taken into account by modifying the calculation of the light time as follows
Many of the observations which we used were given in a B1950 terrestrial equatorial reference frame. Shifting from the J2000 reference frame to the B1950 frame can be done for example using the method of Aoki (1983). But the treatment of the partial derivatives (see Paper I, Sect. 4) becomes particularly complex as there is more than just translation and rotation (which would not change the partial derivative values) to introduce. For this reason, we chose to carry out all our adjustments in the equatorial reference frame J2000, and used the Aoki formula to transform the B1950 coordinates in J2000.
The astrometrical corrections are generally done by the observer. However, we corrected the refraction of the series of observations of D. Pascu 1986-1990, which were communicated to us in an apparent reference frame.
The numerical integrator delivers positions in Cartesian coordinates in a J2000 Jovicentric terrestrial equatorial reference frame. Using the DE406 ephemerides, the positions can be shifted in a geocentric J2000 reference frame (or J2000 heliocentric in the case of the mutual eclipses). This step introduces only one translation of the reference frame, so the partial derivatives remain unchanged. We finally have to transform the positions and partial derivatives in the observational variables.
Let us denote by
![]() the right ascensions and declinations of the satellite Pi at the
observational time tk. It is thus necessary to transform these variables to Cartesian coordinates in the Jovicentric reference frame
(see Fig. 1).
the right ascensions and declinations of the satellite Pi at the
observational time tk. It is thus necessary to transform these variables to Cartesian coordinates in the Jovicentric reference frame
(see Fig. 1).
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{1271fig7.eps}
\end{figure}](/articles/aa/full/2004/43/aa1271/Timg9.gif) |
Figure 1: Transformation of the Jovicentric Cartesian coordinates to the absolute coordinates. |
| Open with DEXTER | |
Denoting (X,Y,Z) the coordinates of Jupiter and
(xi, yi, zi) the Cartesian coordinates of the satellite Pi,
we have the equalities
| X+xi | = | ||
| Y+yi | = | (3) | |
| Z+zi | = |
However, the position of the Galilean satellites relative to the observer depends on the Jupiter ephemerides (for which the precision is approximately 50 km). In order not to introduce an external error from the model, it is thus advisable to go back to differential coordinates (inter-satellite coordinates).
In the case of the tangential coordinates, the satellites' position refers directly to Jupiter, so external errors from planetary ephemerides do not occur. But in this case, it is the unknown difference between the photocentre and the centre of mass of Jupiter which again leads us to use inter-satellite coordinates.
Table 2: Initial conditions at the Julian epoch 2 433 282.5 (01/01/1950, 0H00 TT) found after fitting our numerical model to the observations. The positions are given in ua and the velocities in ua.day-1.
The inter-satellite method requires us to consider a satellite as a reference. In order to not privilege a particular satellite we referred the position of all satellites to the barycentre of the observed satellites. Indeed, the Galilean satellites may not be observable all together in one night. This barycentre was thus calculated for each observation.
We used absolute inter-satellite coordinates relating to the barycentre of the observed satellites.
Let
![]() be the number of observed satellites for a given observation at time tk, and
be the number of observed satellites for a given observation at time tk, and
![]() the observed positions so that we have the equalities
the observed positions so that we have the equalities
![]() and
and
![]() .
We thus have to consider the differences
.
We thus have to consider the differences
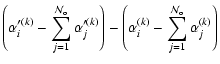 |
(7) |
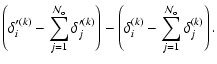 |
(8) |
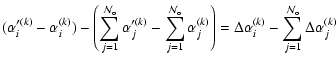 |
(9) |
We thus carried out our fit in equatorial J2000 differential coordinates. The dynamical model used is the one presented in Paper I Sect. 3.4.2. It includes, beside the usual perturbations, the additional oblateness forces and the satellites' triaxiality introducing the J2(k), c22(k) coefficients. To preserve computational time, we used a constant step size of 0.08 day, and a variable step size to complete the integration to the time of the observation tk. To reduce the numerical error, we integrated the dynamical model back and forth starting at the Julian epoch 2 433 282.5 (01/01/1950 at 0H00) which is close to the middle of the time span [1891-2003], using G5 ephemerides as initial conditions.
The control of the numerical error can still be done as in Paper I, integrating back and forth over one century and looking at the variations from
the initial conditions. But this method is rather poor for controlling the partial derivative integration. Indeed, these latter have very strong variations
and even using double precision, the roundoff errors accumulate rapidly. This does not mean that the integration is poor,
but just that the back and forth method is unusable. Thus we performed two integrations, only modifying one initial condition by a small value
![]() .
We then tested the linear relation
.
We then tested the linear relation![]() , following notations of Paper I
, following notations of Paper I
Finally, four iterations by the least-squares method were necessary to minimize the residuals.
With the exception of the mutual phenomena observations, a uniform weighting was used. All these observations thus have a weight of 1. The observations of mutual phenomena are published with weights changing from 1 to 2 and were preserved just as they were in our adjustment.
A frequent difficulty in the adjustments relates to the problem of the correlations between the initial conditions and parameters.
For example, it is well-known that the coefficients J2 and J4 are strongly correlated. Thus
a very large value of J4 can result after adjusting both parameters, compensating in part for the J2 value in the model. In order to avoid
this kind of correlation, we used the values deduced from the space probes for all parameters (see Campbell & Synnott 1985; Anderson et al. 1996; Schubert et al. 1994),
except for the angles ![]() which parameterise the north Jovian pole in a J2000 equatorial frame. Here we benefit greatly from our study made in Sects. 2 and 3 of Paper I. Indeed, as
we explained, one can easily absorb a certain number of perturbations by slightly changing the
values of the constants of the model. However, as our modeling of the Galilean system is particularly sensitive, we can fix from
the beginning many parameter values as constant without decreasing the quality of the adjustment.
which parameterise the north Jovian pole in a J2000 equatorial frame. Here we benefit greatly from our study made in Sects. 2 and 3 of Paper I. Indeed, as
we explained, one can easily absorb a certain number of perturbations by slightly changing the
values of the constants of the model. However, as our modeling of the Galilean system is particularly sensitive, we can fix from
the beginning many parameter values as constant without decreasing the quality of the adjustment.
Table 2 gives the final initial conditions used in our integrator and Table 3 gives the value of the parameters.
Table 3: Parameters used in our numerical model for fitting the observations (from Campbell & Synnott 1985; Anderson et al. 1996; Schubert et al. 1994). The masses are given in Solar mass, the Jovian equatorial radius Er in ua and the angles in degrees.
The graphs of Fig. 2 give the (O-C)s for each satellite after our adjustment for the old and long focus observations. Let us recall that one second of a degree is approximately equal to 3000 km at the distance of Jupiter.
We can compare with interest the (O-C)s of Fig. 3 for the mutual event observations, with those presented in Lieske (1998) and Kaas et al. (1999). One notes that the (O-C)s resulting from our model are much lower, especially for the campaign of 1991. Moreover, the significant drift in the (O-C)s resulting from the use of E5 theory on the right ascension of Io is not present any more. The hypothesis of these authors, suspecting mainly a systematic effect like albedo variation at the time of Io's observations to explain this drift, may not be necessary.
Figure 4 shows the (O-C)s of FASTT observations. As we can see, the accuracy of these observations is very close to that of mutual events.
Finally, Table 4 gives![]() the values of the mean and standard deviations for the (O-C)s in right ascension and
declination for each satellite.
the values of the mean and standard deviations for the (O-C)s in right ascension and
declination for each satellite.
We have noted initially that the values obtained for the mutual phenomena were very good. That is not surprising given that such observations are related to the observation of a phenomenon (eclipse or occultation) rather than to an astrometrical measurement influenced by the atmospheric turbulence. The values for the right ascension of Callisto are however clearly not as good. This difference may be explained by the presence of significant surface effects on Callisto, and which are not accounted for. Another reason could be that the observations of mutual events involving Callisto are more seldom. Hence, the fit may be less accurate for this satellite, as the other type of observations are proportionally more numerous. The quality of the (O-C)s for these observations proves the quality of our fit.
The results of the old observations have a larger scatter. It is possible that the precision of the measurements taken at that
time was less accurate, but this inaccuracy can also be explained by the reference frame used. Indeed, the reduction of the
old observations
in the B1950 reference frame required the use of the formulae of terrestrial precession. But these formulae have changed with time,
and it is difficult today to know which one was used at the time of the observations.
This problem also applies to the long focus observations taken between 1967 and 1978.
![\begin{figure}
\par\includegraphics[angle=-90,width=7.5cm,clip]{1271fig1.ps}\hspace*{4mm}
\includegraphics[angle=-90,width=7.5cm,clip]{1271fig2.ps}
\end{figure}](/articles/aa/full/2004/43/aa1271/Timg34.gif) |
Figure 2: (O-C)s in seconds of a degree for the old and long focus observations, in right ascension ( left) and declination ( right). |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[angle=-90,width=7.5cm,clip]{1271fig3.ps}\hspace*{4mm}
\includegraphics[angle=-90,width=7.5cm,clip]{1271fig4.ps}
\end{figure}](/articles/aa/full/2004/43/aa1271/Timg35.gif) |
Figure 3: (O-C)s in seconds of a degree for the mutual events observations from 1973 to 1992, in right ascension ( left) and declination ( right). |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[angle=-90,width=7.5cm,clip]{1271fig5.ps}\hspace*{3mm}
\includegraphics[angle=-90,width=7.5cm,clip]{1271fig6.ps}\end{figure}](/articles/aa/full/2004/43/aa1271/Timg36.gif) |
Figure 4: (O-C)s in seconds of a degree for the FASTT observations, in right ascension ( left) and declination ( right). |
| Open with DEXTER | |
Finally we present the linear correlation values given in Tables 5-7. The values higher than 0.8 are written in bold type.
As we expect, the coefficients J2 and J4 are strongly correlated up to 88%. Other constants of our model also seem to be strongly correlated like m2 and vx1 or y2 and vx2. Let us recall however, that these values are partly dependent on the observational errors. Moreover, observations give measurements of the tangential plan of the celestial sphere and we never have access to the full position of the satellites. Hence, one can expect to obtain more correlations between the initial conditions.
The fit of our model provides the L1 ephemerides which are available on the ephemerides server of the IMCCE (http://www.imcce.fr/ephemeride_eng.html). The extrapolation of the numerical integration between each time step was not made as often with Chebyshev polynomials. Indeed we preferred to give a Fourier quasi-periodic representation, as this latter delivers the dynamical frequencies of the system and can be used over a very long time span (much longer than the integration one). A complete study of this representation including Laplacian frequency and amplitude is in progress. So far such a method decreases the internal precision of the numerical model to a few tens of kilometers.
Contrary to the former ephemerides, which were very difficult to fit to the whole set of available observations, we succeeded in fitting the model to all the data. Therefore, our new ephemerides present a real improvement compared with the old ones. Future fits will be done as the number of observations increases and the techniques of reduction are improved, as has been recently done in Vasundhara et al. (2003). A fortran subroutine delivering L1 ephemerides is available on request.
Acknowledgements
The authors would like to thank Dr. D. Pascu for providing us much of his observations done at USNO. We are also greatly indebted to Dr. R. C. Stone for giving us the two years of unpublished observations made with the FASTT program. We would also like to thank Dr. N. Seymour for having improved the English of this paper.