A&A 405, 711-721 (2003)
DOI: 10.1051/0004-6361:20030618

Highly accurate calculation of rotating neutron stars

Detailed description of the numerical methods

M. Ansorg - A. Kleinwächter - R. Meinel

Theoretisch-Physikalisches Institut, University of Jena, Max-Wien-Platz 1, 07743 Jena, Germany

Received 10 January 2003 / Accepted 16 April 2003

Abstract
We give a detailed description of the recently developed multi-domain spectral method for constructing highly accurate general-relativistic models of rapidly rotating stars. For both "ordinary'' and "critical'' configurations, we show using representative examples, how the accuracy improves as the order of the approximation increases. As well as homogeneous fluid bodies, we also discuss models of polytropic and strange stars.

Key words: stars: rotation - stars: neutron - gravitation - relativity - methods: numerical

1 Introduction

The structure and the gravitational field of relativistic, axisymmetric and stationary, uniformly rotating perfect fluid bodies is investigated in order to model extraordinarily compact astrophysical objects like neutron stars. The numerical calculation of these objects was the subject of papers by several authors (see Bonazzola & Schneider 1974; Wilson 1972; Butterworth & Ipser 1975, 1976; Friedman et al. 1986, 1989; Lattimer et al. 1990; Neugebauer & Herold 1992; Herold & Neugebauer 1992; Komatsu et al. 1989a, 1989b; Eriguchi et al. 1994; Stergioulas & Friedman 1995; Bonazzola et al. 1993; for reviews see Friedman 1998 and Stergioulas 1998).

The idea to use a "multi-domain spectral method'' was introduced by Bonazzola et al. (1993, 1998). In their "BGSM-code'', the space of physical coordinates is divided into several subregions, each one of them to be mapped onto a cross product of intervals. The physical field quantities are expressed in a spectral expansion with respect to all coordinates defined on the specific intervals. If the interior region of the star is chosen to be exactly one of the domains, then it is possible to obtain representations of the field quantities that are smooth functions within the cross product of intervals. The spectral expansions then provide a very precise approximation of the field quantities. In particular, this choice for the domains circumvents the occurrence of the Gibbs phenomenon at the star's surface, which appears when non-smooth physical fields (such as the mass-energy density) are expressed in terms of a spectral expansion.

The subject of this paper is a detailed description of our multi-domain spectral method (hereafter "AKM-method'') which led to an accuracy of up to 12 digits for rapidly rotating, strongly relativistic homogeneous fluid bodies (Ansorg et al. 2002). Its further development enabled us to calculate rotating toroidal bodies (the relativistic Dyson rings; see Ansorg et al. 2003a).

The corresponding fundamental features of the AKM-method are as described above for the BGSM-code. However, the methods differ in the following:

1.
Instead of the three domains in the BGSM-code (two of them exterior to the star), we have only two domains, since we do not split up the region exterior to the star.
2.
As described in Bonazzola et al. (1998), the BGSM-code is an iterative scheme with each iteration step consisting of several procedures including the solving of nonlinear Poisson-like equations and the determination of an improved approximation of the star's surface. In the AKM-method, a large set of nonlinear algebraic equations for the unknown spectral coefficients corresponding to all field quantities and the unknown shape of the star's surface is simultaneously solved by a Newton-Raphson method.
3.
For the AKM-method, the restriction to only two domains, one of them exactly corresponding to the interior region of the star, can be maintained when the mass shedding limit is approached. In this limit, the star is characterized by a cusp at its equatorial rim, thus requiring that the inner-most domain of the BGSM-code deviate slightly from the star's interior (see Bonazzola et al. 1998; the resulting Gibbs phenomenon is limited since the displacement is small).
We begin our description of the AKM-method with a review of the line element and Einstein's field equations, boundary, regularity and transition conditions as well as the resulting free boundary value problem. Following this, we provide an introduction to the method in question containing a comprehensive description of the specific spectral field representations and the resulting set of nonlinear algebraic equations that ensures both the validity of the field equations within each domain and the transition conditions at the domains' boundary. In the subsequent section, we apply the AKM-method to "ordinary'' homogeneous, strange as well as polytropic stars (with a polytropic exponent $\Gamma =2$) and display the improvement of the accuracy as the order of the approximation increases. Here, "ordinary'' stars means configurations that are not special in the sense that they neither rotate at the mass shedding limit, possess infinite central pressure, nor show a considerable oblateness, but may be strongly relativistic as in the example given in Table 11 of Nozawa et al. (1998) and Table 1 of Ansorg et al. (2002).

Then we give representative examples concerning the excluded "critical'' configurations. At first, we consider homogeneous, strange as well as polytropic stars at the mass shedding limit. Following this, we study homogeneous configurations with an infinite central pressure. Finally, the last part of this section is devoted to highly flattened homogeneous bodies.

In what follows, units are used in which the speed of light as well as Newton's constant of gravitation are equal to 1.

2 Line element, Einstein's field equations, and the free boundary value problem

We use two different formulations of the line element describing the gravitational field of a uniformly rotating perfect fluid body[*]. The corresponding Lewis-Papapetrou coordinates  $(\rho,\zeta,\varphi,t)$ are uniquely defined by the requirement that the metric coefficients and their first derivatives be continuous at the surface of the body.

Exterior to the star in question we write:

$\displaystyle {\rm d}s^2={\rm e}^{2\alpha}({\rm d}\rho^2+{\rm d}\zeta^2) +W^2{\rm e}^{-2\nu}({\rm d}\varphi-\omega~ {\rm d}t)^2 -{\rm e}^{2\nu}{\rm d}t^2$     (1)

while for the interior we take metric functions valid in the comoving frame of reference:
$\displaystyle {\rm d}s^2={\rm e}^{-2U'}[{\rm e}^{2k'}({\rm d}\rho^2+{\rm d}\zeta^2)+W^2 {\rm d}\varphi'^2] -{\rm e}^{2U'}({\rm d}t+a'{\rm d}\varphi')^2.$     (2)

Here, the only new coordinate is $\varphi'=\varphi-\Omega t$ where $\Omega$ is the (constant) angular velocity of the star.

Hence, we get the following transformation formulae:

 
$\displaystyle W^{-1}{\rm e}^{2\nu}\pm(\omega-\Omega) =\left(W{\rm e}^{-2 U'}\mp a'\right)^{-1}, \quad \alpha=k'-U'.$     (3)

The exterior field equations following from the above line element read as follows[*]:
 
                   $\displaystyle \triangle_W^{(1)}\nu$ = $\displaystyle \frac{1}{2}W^2{\rm e}^{-4\nu} (\omega_\rho^2+\omega_\zeta^2)$ (4)
$\displaystyle \triangle_W^{(3)}\omega$ = $\displaystyle 4 (\nu_\rho\omega_\rho+\nu_\zeta\omega_\zeta)$ (5)
$\displaystyle \triangle_2 W$ = 0 (6)

with the abbreviations
                         $\displaystyle \triangle_2$ = $\displaystyle \partial^2_\rho+\partial^2_\zeta$ (7)
$\displaystyle \triangle_W^{(j)}$ = $\displaystyle \triangle_2+ j~W^{-1}(W_\rho\partial_\rho +W_\zeta\partial_\zeta).$ (8)

Since in the comoving frame the energy-momentum tensor reads
$\displaystyle T^{ik}=(\mu+p)u^iu^k+pg^{ik}~,\quad u^k={\rm e}^{-U'}\delta_4^k$     (9)

where $\mu$ is the total mass-energy density and p the pressure, the interior field equations assume a particularly simple form[*]:
 
$\displaystyle \triangle_W^{(1)}U'+\frac{1}{2}W^{-2}{\rm e}^{4U'} [(a'_\rho)^2+(a'_\zeta)^2]$ = $\displaystyle 4~\pi {\rm e}^{2(k'-U')}(\mu+3p)$ (10)
$\displaystyle \triangle_W^{(-1)}a' +4 (a'_\rho U'_\rho+a'_\zeta U'_\zeta)$ = 0 (11)
$\displaystyle \triangle_2 W$ = $\displaystyle 16~\pi {\rm e}^{2(k'-U')} ~W~p .$                 (12)

As with the above potential $\alpha$, the metric function k' can be determined via a line integration from the potentials U',a' and W that follows from
 
$\displaystyle \begin{array}{l} \left( \begin{array}{cc} W_\rho & -W_\zeta \\ [... ...\frac{1}{2}W^{-1}{\rm e}^{4U'} a'_\rho a'_\zeta \end{array}\right), \end{array}$     (13)

such that along the rotation axis $\rho=0$ the condition
 
$\displaystyle {\rm e}^{k'}=\lim_{\rho\to 0} \frac{W(\rho,\zeta)}{\rho}$     (14)

holds. Additionally, for a given equation of state, $p=p(\mu) $ or $\mu=\mu(p)$, the relativistic Euler equations $T^{ik}_{\;;k}=0$ yield $\mu$ and p in terms of the metric potential U':
 
$\displaystyle {\rm e}^{U'}\exp\left[\int_0^p\frac{{\rm d}p'}{\mu(p')+p'}\right] ={\rm e}^{V_0}=\mbox{const.}$     (15)

Hence, for the exterior potentials $\nu,\omega,W$ as well as for the interior potentials U',a',W, particular systems of partial differential equations emerge. At the surface B of the star, the pressure p vanishes, which leads to a constant surface potential U'=V0, see Eq. (15). If additionally the boundary B as well as the corresponding boundary values of the potentials a' and W were given, we would have to solve a particular interior and exterior boundary value problem of the respective field equations, completed by regularity conditions along the rotation axis (here, the $\rho$-derivatives of $\nu,\omega,W/\rho,U'$ and a' vanish) and at infinity (here $\nu\to 0$, $\omega\to 0$ and $W-\rho\to 0$). However, we have to deal with a free boundary value problem, where both the boundary B and the values of a' and W at B are unknown, but have to be determined such that the normal derivatives of the potentials U', a'and W behave continuously at B [*].

For a given equation of state, the corresponding solution depends on two parameters, e.g. the angular velocity $\Omega$ and the gravitational mass M. Note that there might be multiple solutions corresponding to a specific prescribed parameter pair. For the description of the AKM-method, we consider at first the particular prescription of the pair $(V_0,\Omega)$, but treat in a separate subsection the possible prescription of other parameter pairs.

Together with the regularity conditions along the rotation axis, we assume that all metric potentials possess reflectional symmetry with respect to the equatorial plane $\zeta=0$, leading to a vanishing $\zeta$-derivative in this plane (see, for example, Meinel & Neugebauer 1995).

   
3 Description of the method

A function, defined and analytic on a closed interval, can be represented by a rapidly converging Chebyshev-expansion. The spirit of the AKM-method is to use this property for all gravitational potentials, boundary values, and the unknown shape of the surface, which therefore need to be defined on appropriate cross products of intervals. The corresponding Chebyshev-coefficients are determined by a high-dimensional nonlinear set of algebraic equations that encompasses both field equations and transition conditions and is solved by a Newton-Raphson method.

   
3.1 The mappings of the subdomains

As already mentioned in the introduction, we divide the total space of physical coordinates into two subregions, an inner domain covering exactly the interior region of the star, and an outer one encompassing the exterior vacuum region. Both subregions are mapped onto the square $I^2=[0,1]\times[0,1]$, which we realize by introducing a non-negative function $y_{\rm B}$ defined on the interval I=[0,1] that describes the surface of the body by

 
$\displaystyle \begin{array}{lcl} B=\{(\rho,\zeta)\mbox{:}\quad\rho^2=r_{\rm e}^... ...eq t\leq 1\}, &&\\ [5mm] y_{\rm B}(0)=1~,\quad y_{\rm B}(1)=0~ . &&\end{array}$     (16)

Here $r_{\rm e}$ and $r_{\rm p}$ are the equatorial and polar coordinate radii of the body respectively.

A particular example for the mapping in question is given by

 
$\displaystyle \rho^2=r_{\rm e}^2\hspace*{0.1mm}s\hspace*{0.1mm}t~,\quad \zeta^2=r_{\rm p}^2\hspace*{0.1mm}s\hspace*{0.1mm}y_{\rm B}(t)~,\quad (s,t)\in I^2$     (17)

for the interior region and
 
$\displaystyle \rho^2=\frac{r_{\rm e}^2\hspace*{0.1mm}t}{s^2}~,\quad \zeta^2=\frac{r_{\rm p}^2\hspace*{0.5mm}y_{\rm B}(t)}{s^2}~,\quad (s,t)\in I^2$     (18)

for the region exterior to the star. In this manner, the axis $\rho=0$ and the plane $\zeta=0$ are mapped to the coordinate boundaries t=0 and t=1 respectively. Furthermore, the surface B of the body is characterized by s=1. For the interior and exterior transformation, the point s=0 corresponds to the origin and to infinity respectively.

Writing $\rho^2$ and $\zeta^2$ (and not $\rho$ and $\zeta$) in terms of the new variables s and t already takes the regularity condition along the rotation axis as well as the reflectional symmetry with respect to the equatorial plane into account. Indeed, for any potential that is analytic with respect to the variables s and t, it follows that the $\rho$-derivative at $\rho=0$ as well as the $\zeta$-derivative at $\zeta=0$ vanishes provided the above coordinate transformation is invertible there. The latter condition is only violated for s=0[*].

It turns out that the requirements of the regularity of the potentials (as functions of s and t) at t=0 and t=1 replace a particular boundary condition here, that usually must be imposed. Similarly, the regularity of the interior potentials supersedes a boundary condition at the coordinate's origin. However, the asymptotic behaviour at infinity still must be considered, see Sect. 3.2.

Note that for critical configurations we need to modify the above mapping, see Sects. 4.2.1 and 4.2.3.

   
3.2 The representations of the potentials and the surface

For each of the gravitational potentials we use a specific Chebyshev-expansion that takes known boundary and transition conditions into account. In particular we know ( $r^2=\rho^2+\zeta^2$):

 \begin{displaymath} \lim\limits_{r\to \infty}(r \nu)=-M,\qquad \lim\limits_{r\to \infty}(r^3\omega)=2J, \end{displaymath} (19)


$\displaystyle \begin{array}{lcl} \left\vert~\lim\limits_{r\to \infty}r^2~(W\rho... ...\lim\limits_{\rho\to 0}W\rho^{-1}\right\vert&\;<\;&\infty,\\ [4mm] \end{array}$     (20)

where M and J are the gravitational mass and the angular momentum of the star, respectively, see also Eqs. (56, 57) for an integral representation. Therefore we write outside the star:

                                         $\displaystyle \nu = s\left[\nu_{\rm B}(t)+(s-1)H_\nu (s,t)\right]$ (21)
    $\displaystyle \omega = s^3\left[\omega_{\rm B}(t)+(s-1) H_\omega (s,t)\right]$ (22)
    $\displaystyle W^{\rm (ext)} = \rho\;\left(1+s^2\; \left[\hat{W}_{\rm B}(t)+(s-1)H_{W,\rm ext} (s,t)\right]\right)$ (23)

and inside
                                    U' = V0+(s-1)HU'(s,t) (24)
    $\displaystyle a' = \rho^2\left[\hat{a}'_{\rm B}(t)+(s-1)H_{a'}(s,t)\right]$ (25)
    $\displaystyle W^{\rm (int)} = \rho\;\left[1+\hat{W}_{\rm B}(t)+(s-1)H_{W,\rm int}(s,t)\right].$ (26)

Here, the boundary values $a'_{\rm B},W_{\rm B}$ of the potentials a',W are expressed by the functions $\hat{a}'_{\rm B},\hat{W}_{\rm B}$ in the following manner:
       $\displaystyle W_{\rm B}$ = $\displaystyle \rho(\hat{W}_{\rm B}+1)$ (27)
$\displaystyle a_{\rm B}$ = $\displaystyle \rho^2\;\hat{a}'_{\rm B}.$ (28)

The above one- and two-dimensional functions are expressed as limits of Chebyshev-expansions, e.g. [*]
                                     $\displaystyle \nu_{\rm B}(t)=\lim\limits_{m\to\infty} \nu_{\rm B}^{(m)}(t),$ (29)
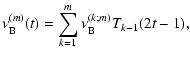    $\displaystyle \nu_{\rm B}^{(m)}(t)=\sum\limits_{k=1}^m \nu_{\rm B}^{(k;m)} T_{k-1}(2t-1),$ (30)
    $\displaystyle H_\nu (s,t)=\lim\limits_{m\to\infty} H_\nu^{(m)}(s,t),$ (31)
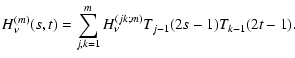    $\displaystyle H_\nu^{(m)} (s,t)=\sum\limits_{j,k=1}^m H_\nu^{(jk;m)} T_{j-1}(2s-1)T_{k-1}(2t-1).$ (32)

Similarly, taking into account the representation of the boundary in (16), we write the boundary function $y_{\rm B}$ as follows[*]
                               $\displaystyle y_{\rm B}=(1-t)\;[1+r_{\rm p}^{-2}tg(t)],$ (33)
    $\displaystyle g(t)=\lim\limits_{m\to\infty} g^{(m)}(t),$ (34)
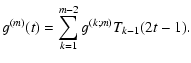    $\displaystyle g^{(m)}(t)=\sum\limits_{k=1}^{m-2} g^{(k;m)} T_{k-1}(2t-1).$ (35)

In the order m of our approximation scheme, we establish a nonlinear set of algebraic equations that determines the above coefficients of the $m{\rm th}$ Chebyshev-expansion. In the limit $m\to\infty$, this set of algebraic equations is equivalent to the free boundary value problem in question, and the $m{\rm th}$ approximation becomes the solution.

   
3.3 The nonlinear set of algebraic equations

For a given equation of state, we specify the solution of our free boundary value problem by the prescription of a particular parameter pair. At first let us take ( $V_0,\Omega$); a more general choice will be discussed in Sect. 3.5.

We express the boundary values $\nu_{\rm B}$ and $\omega_{\rm B}$ in terms of  $(V_0,\Omega)$ and the functions $a'_{\rm B}$ and $W_{\rm B}$, see Eqs. (3). This ensures the continuity conditions of the field potentials at the star's surface[*]. Hence, in the order m of our approximation scheme, we take the two-dimensional Chebyshev-coefficients

$\displaystyle H^{(jk;m)}_\nu, H^{(jk;m)}_\omega, H^{(jk;m)}_{W,\rm ext}, H^{(jk;m)}_{U'}, H^{(jk;m)}_{a'}, H^{(jk;m)}_{W,\rm int}$     (36)

as well as the one-dimensional Chebyshev-coefficients
$\displaystyle (\hat{a}'_{\rm B})^{(k;m)}, \hat{W}_{\rm B}^{(k;m)}, g^{(k;m)}$     (37)

as independent variables. They build up a vector ${\vec x}^{(m)}$ consisting of
$\displaystyle m_{\rm total}=6 m^2+3m$     (38)

components. The first 6m2 components comprise all two-dimensional Chebyshev-coefficients while the following 3m-2 are the above one-dimensional Chebyshev-coefficients. The remaining two entries are filled by the values of $r_{\rm e}$ and $r_{\rm p}$.

We now describe in detail the components of a vector

$\displaystyle {\vec f}^{(m)}={\vec f}^{(m)}({\vec x}^{(m)})$     (39)

also consisting of $m_{\rm total}$ components that must vanish for the solution ${\vec x}^{(m)}$ of the $m{\rm th}$-order approximation.

Given an arbitrary vector ${\vec x}^{(m)}$, we compute the Chebyshev coefficients corresponding to the first and second derivatives of the functions[*]

 \begin{displaymath} H^{(m)}_\nu, H^{(m)}_\omega, H^{(m)}_{W,\rm ext}, H^{(m)}_{U'}, H^{(m)}_{a'}, H^{(m)}_{W,\rm int}\end{displaymath} (40)

and
$\displaystyle (\hat{a}'_{\rm B})^{(m)}, \hat{W}_{\rm B}^{(m)}, g^{(m)}$     (41)

with respect to s and t. Together with the coordinate transformations (17, 18), we therewith find the first and second spatial derivatives of all gravitational potentials with respect to the coordinates $\rho$ and $\zeta$ in our $m{\rm th}$-order approximation, at an arbitrary grid point inside the domains (not at the origin or at infinity). So, we may fill the first 3m2 entries of ${\vec f}^{(m)}$ with the differences of right and left hand sides of the exterior Eqs. (4), evaluated at m2 gridpoints $(s_j,t_k), j,k=1\ldots m$, corresponding to spatial points outside the star. Following the spirit of the spectral methods and in order to ensure a rapid convergence, we take for the sj and tj the roots of the $m{\rm th}$ Chebyshev polynomial, i.e.

 \begin{displaymath} s_j=t_j=\cos^2\left(\pi~\frac{2j-1}{4m}\right)\quad(s_j,t_j>0).\end{displaymath} (42)

For the subsequent 3m2 components of ${\vec f}^{(m)}$, we first compute the two-dimensional, $m{\rm th}$-order Chebyshev coefficients corresponding to the interior function k'. This is done by determining the Chebyshev coefficients corresponding to the t-derivative of k' using (13) and again the coordinate transformation (17), and after that, by integrating with respect to the axis condition (14), see footnote 9. So, the 3m2 entries in question can now be filled with the differences of right and left hand sides of the interior Eqs. (10), again evaluated at the m2 gridpoints (sj,tk)here corresponding to spatial points inside the star.

The remaining 3m components of our vector ${\vec f}^{(m)}$ are formed from the differences of the $m{\rm th}$-order interior and exterior normal derivatives of the gravitational potentials $\nu,\omega$ and W, evaluated at the m surface grid points (s=1,tk). Note that the coordinate transformations (17, 18) are regular here, and thus the normal derivatives can easily be computed using the shape of the star that is incorporated in ${\vec x}^{(m)}$. The interior normal derivatives of $\nu$ and $\omega$ follow from the transformation formulae (3) and the interior potentials.

In this manner we get in the $m{\rm th}$ approximation order a nonlinear set of $m_{\rm total}=6 m^2+3m$ algebraic equations

 \begin{displaymath} {\vec f}^{(m)}({\vec x}^{(m)})=0\end{displaymath} (43)

that is solved by a Newton-Raphson method, see Sect. 3.4.

   
3.4 The Newton-Raphson method and the initial solution

In the Newton-Raphson method, the zero of a nonlinear set of algebraic equations of the form (43) is determined iteratively,

 \begin{displaymath} {\vec x}^{(m)}_n={\vec x}^{(m)}_{n-1} -\left[\left.\frac{\p... ...(m)}_{n-1}}\right]^{~-1} {\vec f}^{(m)}({\vec x}^{(m)}_{n-1})~,\end{displaymath} (44)

requiring an initial ${\vec x}^{(m)}_0$ which must already be sufficiently close to the final solution ${\vec x}^{(m)}=\lim_{n\to\infty}{\vec x}^{(m)}_n$. The Jacobi matrix in the Eq. (44) is determined approximately using ( $\epsilon\ll 1$)
 
$\displaystyle \left[\left.\frac{\partial~ {\vec f}^{(m)}}{{\partial~ {\vec x}}^... ...ight) - {\vec f}_A^{(m)}\left({\vec x}^{(m)}-\epsilon~{\vec e}_B\right)\right].$     (45)

Here the subscripts A and B denote the corresponding element of the Jacobi matrix and the vector ${\vec f}^{(m)}$, and ${\vec e}_B$is the $B{\rm th}$ unit vector, $({\vec e}_B)_A=\delta_{AB}$.

There are various possibilities for obtaining an initial solution. For example, one may start from the static solution characterized by $\Omega=0$. Here the corresponding field equations turn into ordinary differential equations with respect to the radial coordinate r, and these can be solved e.g. by using a Runge-Kutta-method. Taking this solution for the initial ${\vec x}^{(m)}_0$, one may now gradually increase the parameter $\Omega$ and thus eventually explore the whole parameter space. Another possibility is to start with a Newtonian solution (e.g. a Maclaurin spheroid). Proceeding into the relativistic regime comes about by increasing the absolute value of V0.

In our treatment we favoured the latter initialization, for it already provides highly distorted bodies. Moreover, we calculated configurations with a particular equation of state by starting from a constant mass-energy density profile and continuously moving to the desired equation of state.

   
3.5 Arbitrary parameter prescription

With a slight modification of our nonlinear set of equations described in Sect. 3.3, we are able to take various different parameter prescriptions into account. The idea is to add the quantities $\Omega$ and V0 to the vector ${\vec x}^{(m)}$, resulting in $m_{\rm total}=6m^2+3m+2$ unknowns from now on. Simultaneously, we add two equations to the nonlinear set representing exactly the desired parameter relation for the solution in question. This can be done since all physical quantities concerning the final solution are now contained in the vector ${\vec x}^{(m)}$.

For example the potential $U'_{\rm c}$ at the origin reads[*]

$\displaystyle U'_{\rm c}=V_0-H_{U'}(0,0),$     (46)

which is directly connected to the central pressure $p_{\rm c}$, see Eq. (15). Likewise, M and J can be expressed
                   M = $\displaystyle - r_{\rm p}\left[\nu_{\rm B}(0)-H_\nu (0,0)\right],$ (47)
J = $\displaystyle \frac{1}{2}r_{\rm p}^3\left[\omega_{\rm B}(0)- H_\omega (0,0)\right].$ (48)

Also the prescription of a parameter $\beta$ is possible which controls the distance of a configuration to the mass shedding limit:

 \begin{displaymath} \beta=-\frac{{\rm d} y_{\rm B}}{{\rm d}t}\;(t=1)=\left\{ \b... ...\\ 1 & \mbox{for an ellipsoidal shape.} \end{array}\right. \end{displaymath} (49)

Similarly, one can prescribe more complicated expressions such as the baryonic mass M0, which is defined by an integral over the interior field quantities.

Table 1: Results for a constant mass-energy density model ($\mu =\mu _0$) with $\bar{p}_{\rm c}=1$, $r_{\rm p}/r_{\rm e}=0.7$. Here, $\bar{p}_{\rm c}=p_{\rm c}/\mu_0$, $\bar{\Omega}=\Omega/\mu_0^{1/2}$, $\bar{M}=M \mu_0^{1/2}$, $\bar{R}_{\rm circ}={R}_{\rm circ}~\mu_0^{1/2}$ and $\bar{J}=J\mu_0$ are normalized values of the physical quantities, see Eqs.  (56, 57). Apart from the virial identities GRV2 and GRV3 in the $m{\rm th}$ order approximation, the Cols. 3-11 display the relative deviation of the specific quantity in the $m{\rm th}$ order approximation with respect to the numerical result obtained for m=24. The quantities $M_{\rm in},J_{\rm in}$ and $M_{\rm out},J_{\rm out}$ refer to the corresponding numerical values resulting from (56, 57) and (19) respectively.

Any two conditions of this kind (of which the above ones are just examples) can be taken and added to the system of nonlinear equations. The corresponding parameters (here  $p_{\rm c}, M,J,\beta$ or M0) must then be prescribed. In this paper we concentrate on the pair $(p_{\rm c},r_{\rm p}/r_{\rm e})$ and only take $(p_{\rm c},\beta)$in order to place ourselve exactly on the mass shedding limit, see Sect. 4.2.1.

   
3.6 Regularity and uniqueness

As already depicted in Sect. 3.1, the AKM-method is characterized by the fact that some of the usual boundary conditions are replaced by regularity requirements. Moreover, if for the moment we only consider the functions

 \begin{displaymath} H_\nu, H_\omega, H_{W,\rm ext}, H_{U'}, H_{a'}, H_{W,\rm int}\end{displaymath} (50)

and treat the quantities $r_{\rm e},r_{\rm p},\Omega,V_0$ as well as the functions  $a'_{\rm B},W_{\rm B}$ and g as if they were given, we obtain specific partial differential equations valid in I2, and particular boundary conditions at any edge of I2 are not required for any of the functions listed in (50). Nevertheless, the solution of this system of equations is uniquely determined if we require regularity with respect to all functions. A similar situation can be studied in the one-dimensional case, e.g. the equation ( $\;\dot{}= {\rm d}/{\rm d}t$)
$\displaystyle t(1-t)\ddot{h}+2(1-2t)\dot{h}-2h+2=0\Leftrightarrow [t(1-t)h]^{\cdot\cdot}=-2$     (51)

possesses only the solution $h\equiv 1$ which is regular within I.

The above approximation scheme sorts out the non-regular solutions since it is based on Chebyshev-expansions. It moreover ensures known, additional properties of the functions (50) at s=0, e.g.  $H_{U'}(s=0,t)=\rm const$. Note that these properties are approached as $m\to\infty$.

   
4 Representative examples

   
4.1 Ordinary stars

At first we apply the AKM-method to three models of homogeneous (Eqs. (52)), polytropic (with a polytropic exponent $\Gamma =2$, Eqs. (53)), and strange stars (Eqs. (54)). In particular, we prescribe the corresponding equation of state in the form $\mu=\mu(p)$ and find from Eq. (15) the relation to the interior potential U':

   
                                              $\displaystyle \mu~(p)=\mu_0={\rm const}\Rightarrow\left\{ \begin{array}{lcl} p&... ...u_0\left({\rm e}^{V_0-U'}-1\right) \\ [3mm] \mu&\;=\;&\mu_0 \end{array}\right.$ (52)
    $\displaystyle \mu~(p)=p+\sqrt{p/K}\Rightarrow\left\{ \begin{array}{lcl} p&\;=\;... ...\\ [3mm] \mu&\;=\;&\left({\rm e}^{2~(V_0-U')}-1\right)/(4K) \end{array}\right.$ (53)
    $\displaystyle \mu~(p)=4B+3p\Rightarrow\left\{ \begin{array}{lcl} p&\;=\;&B\left... ...) \\ [3mm] \mu&\;=\;&B\left(1+3{\rm e}^{4~(V_0-U')}\right). \end{array}\right.$ (54)

Here, K and B are the polytropic constant and the MIT bag constant, respectively[*]. Note that for the application of the AKM-method (strictly speaking, only for its rapid convergence) it is necessary to have analytic dependencies p=p(U') and $\mu=\mu(U')$, in particular at U'=V0. For the equation of state, $\mu=\mu(p)$, this requires that
$\displaystyle \mu=p^{N/(N+1)}f[p^{1/(N+1)}]$     (55)

where f is some function which is positive and analytic when its argument vanishes, and N is some non-negative integer. Apart from the homogeneous and the strange star model, this condition is met for polytropic equations of state with a polytropic exponent $\Gamma=1+1/N$ when N is a non-negative integer (as in the case above where N=1). In order to treat more general equations of state, one needs to consider several layers inside the star, with each one of them characterized by a specific equation of state. The outermost one of them again must meet the above requirement. The consideration of several layers leads to a corresponding number of subregions into which the interior domain needs to be split.

In Tables 1 to 3 one finds numerical values of several physical quantities, for a specified configuration with prescribed central pressure $p_{\rm c}$(equivalently, for non-homogeneous models, we may prescribe the central mass-energy density $\mu_{\rm c}$, see Table 2) and radius ratio $r_{\rm p}/r_{\rm e}$. The angular momentum J, gravitational mass M, equatorial circumferential radius ${R}_{\rm circ}$ and the polar redshift $Z_{\rm p}$ are given by:

  
                                     J = $\displaystyle -2\pi\int(\mu+p)a'{\rm e}^{2k'-2U'}W{\rm d}\rho {\rm d}\zeta$ (56)
M = $\displaystyle 2\Omega J+2\pi\int(\mu+3p){\rm e}^{2k'-2U'}W{\rm d}\rho {\rm d}\zeta$ (57)


$\displaystyle \begin{array}{lcl} R_{\rm circ}&=&{\rm e}^{-V_0}\left[W\sqrt{1-u^... ..._{~(\rho=r_{\rm e},~\zeta=0)}\\ [4mm] Z_{\rm p}&=&{\rm e}^{-V_0}-1 \end{array}$                                          (58)

with $u=-W^{-1}a'{\rm e}^{2U'}$. Note that the above integrals extend over the space of $\rho$- and $\zeta$-coordinates covering the interior of the body[*].

Table 2: Results for a polytropic model (polytropic exponent $\Gamma =2$, polytropic constant K) with $\bar{\mu}_{\rm c}=1$, $r_{\rm p}/r_{\rm e}=0.834$. Here, $\bar{\mu}_{\rm c}=K\mu_{\rm c}$, $\bar{\Omega}=K^{1/2}\Omega$, $\bar{M}=K^{-1/2}M $, $\bar{R}_{\rm circ}=K^{-1/2}{R}_{\rm circ}$ and $\bar{J}=K^{-1}J$ are normalized values of the physical quantities, see Eqs. (56, 57). For the meaning of the quantities listed in the Cols. 3-11, see Table 1.

Table 3: Results for a strange star model (MIT bag constant B) with $\bar{p}_{\rm c}=2$, $r_{\rm p}/r_{\rm e}=0.5$. Here, $\bar{p}_{\rm c}=B^{~-1}p_{\rm c}$, $\bar{\Omega}=B^{~-1/2}\Omega$, $\bar{M}=B^{1/2}M $, $\bar{R}_{\rm circ}=B^{1/2}{R}_{\rm circ}$ and $\bar{J}=BJ$ are normalized values of the physical quantities, see Eqs. (56, 57). For the meaning of the quantities listed in the Cols. 3-11, see Table 1.

A first test of the accuracy of a solution determined numerically is the comparison of the calculations of M and J from the exterior fields (see Eqs. (19)) with those from the above integral representations (56, 57). A further check is given by the general-relativistic virial identies GRV2 and GRV3, derived by Bonazzola & Gourgoulhon (1994) and Gourgoulhon & Bonazzola (1994). As a consequence of the field equations, they identically vanish for an exact analytic solution corresponding to a stationary and asymptotically flat spacetime. Particularly, for our rotating star models they read

$\displaystyle GRV3=\vert 1-I_1/I_2\vert,\quad GRV2=\vert 1-J_1/J_2\vert$     (59)

with:

  \begin{eqnarray*} I_1&=& 4\pi\int\left[3p\sqrt{1-u^2}+(\mu+p)\frac{u^2}{\sqrt{... ...\nu}\left(\nabla\omega\right)^2\right]{\rm d}\rho~ {\rm d}\zeta \end{eqnarray*}


(we use the abbreviations $u=-W^{-1}a'{\rm e}^{2U'},~\rho{\rm e}^{\eta}=W{\rm e}^{-\nu}$). The Nabla-operator has its usual meaning, in terms of the coordinates $\rho$ and $\zeta$, i.e. for any two functions a and b
$\displaystyle \left(\nabla a\right)^2=a_\rho^2+a_\zeta^2,\quad \nabla a\nabla b=a_\rho b_\rho+a_\zeta b_\zeta.$     (60)

The above integrals are taken over the whole space of $\rho$- and $\zeta$-coordinates (for I1 and J1 this reduces again to the interior region of the star since both pressure p and energy-mass density $\mu$ vanish outside the body).

Apart from the values for the above physical quantities with the accuracy that was reached in the $24{\rm th}$ approximation order, we provide in Tables 1-3 the improvement of the accuracy as the order m is increased. Also given are the corresponding numerical values of the general-relativistic virial identies GRV2 and GRV3 as well as those of the relative deviations concerning the integral and far-field representations of M and J.

We note generally an exponential convergence of the numerical solution as the order m increases. This is a common feature of the spectral methods. However, the star's field quantities may vary in their "smoothness'' resulting in a variably rapid convergence. For example, the convergence of the numerical solution corresponding to the homogeneous star (Table 1) is much faster than that corresponding to the strange one (Table 3). In a sense, the strange star is closer to the mass-shedding limit (here $\beta\approx 0.39$ while for the homogeneous model $\beta\approx0.84$) and moreover more flattened.

The models in Tables 1 and 2 have been calculated by Nozawa et al. (1998). Note that for the polytropic model there is a steeper gradient of the pressure as a function of the radial coordinate r, e.g. within the equatorial plane. In order to take this property into account, we used for this model the following slightly modified interior coordinate transformation

 
$\displaystyle \rho^2=r_{\rm e}^2\hspace*{0.1mm}\sigma(s~;c_{\rm s})\hspace*{0.1... ...pace*{0.1mm}\sigma(s~;c_{\rm s})\hspace*{0.1mm}y_{\rm B}(t)~,\quad (s,t)\in I^2$     (61)

with
$\displaystyle \sigma(s~;c_{\rm s})=\frac{1-c_{\rm s}}{1-c_{\rm s}s}s$     (62)

and the constant parameter $c_{\rm s}=0.6$ (for the other models we took $c_{\rm s}=0$). Minor modifications of this kind, specially suited to the particular problem in question, may accelerate the convergence, see below for further examples.

   
4.2 Critical stars

   
4.2.1 Stars at the mass shedding limit

The endpoint of a sequence of rotating stars is often marked by a mass shedding limit. It is of particular interest since specific physical quantities such as the angular velocity reach maximal values there. A highly accurate determination of this limit is therefore desirable.

The mass shedding limit is reached when the angular velocity $\Omega$ of the star attains the angular velocity of test particles moving on a prograde circular orbit at the star's equatorial rim. For the $\rho$-derivative of the field quantity U' it follows:

$\displaystyle U'_{\rho}(r_{\rm e},0)=0.$     (63)

Moreover, a cusp at the surface occurs (see Fig. 1), which corresponds to a vanishing mass-shedding parameter $\beta$, see Eq. (49).


  \begin{figure} \unitlength1cm \hspace*{-1cm} \par\psfrag{r}[r][r]{{$\rho$ }} \psfrag{q}[r][r]{{$\zeta$ }} \epsfig{file=3477f1.eps,scale=0.7}\par \end{figure} Figure 1: Meridional cross-section of the homogeneous mass-shedding configuration specified in Table 4 (with the axes scaled identically). The dashed curves indicate the boundary of the corresponding ergo-region.
Open with DEXTER


  \begin{figure} \unitlength1cm \hspace*{-1cm} \par\psfrag{t}[r][r]{{$t$ }} \psfra... ...}} \psfrag{0.8}[c][c]{{0.8}} \epsfig{file=3477f2.eps,scale=0.7}\par \end{figure} Figure 2: First derivative of the function g=g(t) with respect to t for the homogeneous Newtonian mass-shedding configuration (A) of Table 2 in Ansorg et al. (2003b). The numerical methods explained in section 3 ibid. have been carried out up to the approximation order N=80.
Open with DEXTER

Numerical investigations of a homogeneous Newtonian configuration rotating at the mass-shedding limit suggest that the surface function gbecomes singular in higher derivatives at this limit, see Fig. 2. This causes a similar singular behaviour of all gravitational potentials, and we expect a failure of the spectral methods. Nevertheless, since the singularities show up only in higher derivatives, it is possible to achieve a slow convergence, see Tables 4-6[*]. However, it is then necessary to modify the coordinate transformations (17, 18) such that the curves $s={\rm const}$ do not possess a cusp (except for s=1). Here we use

 
$\displaystyle \rho^2=r_{\rm e}^2\hspace*{0.1mm}s~t~,\quad \zeta^2=s(1-t)~[r_{\rm p}^2+stg(t)]~,\quad (s,t)\in I^2$     (64)

and
 
$\displaystyle \rho^2=\frac{r_{\rm e}^2 t}{s^2}~,\quad \zeta^2=\frac{(1-t)~[r_{\rm p}^2+stg(t)]}{s^2}~,\quad (s,t)\in I^2$     (65)

for the interior and exterior region respectively.

Table 4: Results for a constant mass-energy density model rotating at the mass-shedding limit with $\bar{p}_{\rm c}=1$. For the meaning of the quantities, see Table 1.

Table 5: Results for a polytropic model (polytropic exponent $\Gamma =2$) at the mass-shedding limit with $\bar{\mu}_{\rm c}=0.34$. For the meaning of the quantities, see Table 2.

Table 6: Results for a strange star model at the mass-shedding limit with $\bar{p}_{\rm c}=3$. For the meaning of the quantities, see Table 3.

From the numerical results listed in Tables 4-6 we may speculate that the behaviour of the pressure at the star's surface (which is determined by the equation of state) affects the type of the above singularities. They seem to be weaker for smoother equations of state, when the pressure and some higher derivatives vanish at the equator.

   
4.2.2 Stars with infinite central pressure

Another possible endpoint of a sequence of rotating stars in General Relativity is reached when the pressure diverges at the star's centre. For example, the sequence of static homogeneous configurations is characterized by this limit. Here, the star is spherical ( $r_{\rm p}=r_{\rm e}$ and g=0), and the corresponding gravitational fields are analytically given by the Schwarzschild solution which reads in our chosen coordinates (with $r^2=\rho^2+\zeta^2$)

                                       $\displaystyle {\rm e}^{U'}=\frac{3\left[1-M/(2r_{\rm e})\right]}{2\left[1+M/(2r_{\rm e})\right]} -\frac{1-Mr^2/(2r_{\rm e}^3)}{2+Mr^2/(r_{\rm e}^3)}$ (66)
    $\displaystyle W{\rm e}^{-U'}=\rho~\frac{\left[1+M/(2r_{\rm e})\right]^{~3}}{1+Mr^2/(2r_{\rm e}^3)}$ (67)
    a'=0 (68)

inside (i.e. for $r<r_{\rm e}$) and
                              $\displaystyle {\rm e}^{\nu}=\frac{1-M/(2r)}{1+M/(2r)}$ (69)
    $\displaystyle W{\rm e}^{-\nu}=\rho~\left[1+M/(2r)\right]^{~2}$ (70)
    $\displaystyle \omega=0$ (71)

outside the star ( $r>r_{\rm e}$). In the limit $Mr_{\rm e}^{-1}\to 1$ the central value  ${\rm e}^{U'_{\rm c}}$ vanishes which corresponds to $p_{\rm c}\to \infty$since the surface potential $V_0=U'(r=r_{\rm e})$ remains finite.


  \begin{figure} \unitlength1cm \hspace*{-1cm} \par\psfrag{r}[r][r]{{$\rho$ }} \psfrag{q}[r][r]{{$\zeta$ }} \epsfig{file=3477f3.eps,scale=0.7}\par \end{figure} Figure 3: Meridional cross-section of a homogeneous configuration with infinite central pressure, specified in Table 7 (with the axes scaled identically). The dashed curves indicate the boundary of the corresponding ergo-region.
Open with DEXTER

Table 7: Results for a homogeneous model with infinite central pressure and $r_{\rm p}/r_{\rm e}=0.7$. For the meaning of the quantities, see Table 1. The virial identities are not defined for $\bar{p}_{\rm c}=\infty$ since the integrals I1,I2,J1,J2 diverge.

A rotating configuration with an infinite central pressure is characterized by an ergo-region that extends in the inside up to the coordinate origin, see Fig. 3. Hence, at this point the space-time violates the requirement of stationarity[*] and therefore some irregular behaviour of the gravitational potentials arises here, which, in the slow rotation limit, has been studied by Chandrasekhar & Miller (1974). Consequently, we again expect a failure of the AKM-method. But as in the case when the mass-shedding limit occurs, we are still able to obtain slowly converging numerical solutions, see Table 7. It is however necessary (i) to modify the Chebyshev representation of the interior gravitational potentials and (ii) to introduce a slightly different coordinate mapping of the interior region. In particular, this is done by writing

                                         $\displaystyle {\rm e}^{U'} ={\rm e}^{V_0}+(s-1)\tilde{H}_{U'}(s,t)$ (72)
    $\displaystyle a'{\rm e}^{U'} = \rho^2\left[\tilde{a}'_{\rm B}(t)+(s-1)\tilde{H}_{a'}(s,t)\right]$ (73)
    $\displaystyle W^{\rm (int)}{\rm e}^{-U'} = \rho\;{\rm e}^{-V_0}\; \left[1+\tilde{W}_{\rm B}(t)+(s-1)\tilde{H}_{W,\rm int}(s,t)\right]$ (74)

and using again the transformation (61). The reformulation of the interior Chebyshev expansions is motivated by the Schwarzschild solution given above. We learn from here that the vanishing of ${\rm e}^{U'_{\rm c}}$ coincides with that of the central value of $W/\rho$. Moreover, we note that the combination
$\displaystyle \rho^{-2}g_{\varphi\varphi}=(\rho^{-1}W{\rm e}^{-U'})^2-(\rho^{-1}a'{\rm e}^{U'})^2$     (75)

remains positive (and finite) at the origin when ${\rm e}^{U'_{\rm c}}\to 0$. So the above reformulation ensures particular dependencies of the metric functions at the origin when ${\rm e}^{U'_{\rm c}}\to 0$.

The use of the transformation (61) allows one to lay the coordinate mesh more densely in the vicinity of the origin. This helps to take the singular behaviour in higher derivatives of the functions $\tilde{H}_{U'},\tilde{H}_{a'}$ and $\tilde{H}_{W,\rm int}$ into account and thus provides a better convergence. For the example given in Table 7 and Fig. 3, we used $c_{\rm s}=0.65$. In the approximation scheme we prescribed the parameters ( ${\rm e}^{U'_{\rm c}},r_{\rm p}/r_{\rm e}$) and finally pushed ${\rm e}^{U'_{\rm c}}$ to zero.

   
4.2.3 Highly flattened stars

As with the situations above, the coordinate transformations (17, 18) need to be modified if one wants to calculate models of strongly distorted stars (such as the examples given in Table 2 of Ansorg et al. 2002). When using (17, 18), then each curve $s={\rm const}$ represents an image which is similar to the star's boundary. This leads for distorted stars to a non-uniform partition of the domains by the coordinate net of (s,t)-variables. Moreover, the oblateness of the configurations suggests adapting the coordinates s and t for the exterior domain to resemble oblate spheroidal coordinates. A possible mapping which takes these considerations into account is given by [ $(s,t)\in I^2$]:

 
                     $\displaystyle \rho^2$ = $\displaystyle r_{\rm e}^2t~\tau(t)~,$ (76)
$\displaystyle \zeta^2$ = $\displaystyle s(1-t)[r_{\rm p}^2+tg(t)]$ (77)

for the interior region and
 
                                $\displaystyle \rho^2$ = $\displaystyle t[r_{\rm e}^2-r_{\rm p}^2+\xi^2(s)][1-s+s\tau(t)],$ (78)
$\displaystyle \zeta^2$ = $\displaystyle (1-t)[\xi^2(s)+tg(t)]$ (79)

exterior to the star with
$\displaystyle \tau(t)=\frac{1}{1-c_{\rm t}(1-t)}~,\quad\xi(s)=r_{\rm p}+\frac{c_{\rm s}}{s}(1-s).$     (80)

For the examples (b) and (c) in Ansorg et al. (2002) we took $c_{\rm s}=0.07$ and $c_{\rm t}=-0.2$ whereas for the example (a) in Ansorg et al. (2002) as well as for that presented in Table 8 the values $c_{\rm s}=0.2$ and $c_{\rm t}=0$ were chosen. Note that the prescribed parameter pair, ( $p_{\rm c},r_{\rm p}/r_{\rm e}$), is the same for the latter two configurations. All other physical quantities are also very similar for these models, including the appearance of the corresponding cross sections. Here, the high accuracy is needed in order to distinguish between these two nearby configurations.


  \begin{figure} \unitlength1cm \hspace*{-1cm} \par\psfrag{r}[r][r]{{$\rho$ }} \psfrag{q}[r][r]{{$\zeta$ }} \epsfig{file=3477f4.eps,scale=0.7}\par \end{figure} Figure 4: Meridional cross-section of a highly distorted homogeneous configuration at the mass shedding limit, specified in Table 9 (with the axes scaled identically).
Open with DEXTER

Table 8: Results for a homogeneous model with $\bar{p}_{\rm c}=0.002$ and $r_{\rm p}/r_{\rm e}=0.2$. For the meaning of the quantities, see Table 1.

Table 9: Results for a highly distorted homogeneous configuration at the mass shedding limit with $\bar{p}_{\rm c}=0.003$. For the meaning of the quantities, see Table 1.

A final example (see Table 9 and Fig. 4) exhibits that even in the highly flattened regime, configurations at the mass shedding limit can be calculated (here $c_{\rm s}=0.2$ and $c_{\rm t}=0$). This particular model is close to the configuration (a) in Ansorg et al. (2003a), which marks the transition body between spheroidal and toroidal configurations at the mass shedding limit. A more detailed investigation of highly flattened homogeneous bodies in General Relativity will be published elsewhere.

Acknowledgements
The authors would like to thank David Petroff and Nik Stergioulas for many valuable discussions. This work was supported by the German Deutsche Forschungsgemeinschaft (DFG-project ME 1820/1-3).

References


Copyright ESO 2003