- ... body
![[*]](/icons/foot_motif.gif)
- The basic principles of the AKM-method rely on a
rapidly converging Chebyshev representation of all physical and geometrical
quantities within appropriate coordinates. The method is therefore applicable
to arbitrary differentially rotating configurations (with some analytical
rotation law).
In this article we restrict ourselves to uniform rotation. In
this case we may use the simpler field equations valid within the comoving frame
of reference.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... follows
![[*]](/icons/foot_motif.gif)
- Once
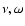 and W are known, the potential
and W are known, the potential
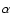 can be determined by a line integral
(with
can be determined by a line integral
(with
 as
as
 ).
).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... form
![[*]](/icons/foot_motif.gif)
- See,
for example, Kramer et al. (1980).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
![[*]](/icons/foot_motif.gif)
- It is a consequence of
the field equations that k' is then also differentiable.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...=0
![[*]](/icons/foot_motif.gif)
- Note that the interior coordinate
transformation introduced in
Sect. 4.2.3 is not invertible
at the equatorial rim of the star, but it is so at s=0.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... e.g.
![[*]](/icons/foot_motif.gif)
- The Chebyshev-polynomials are defined by
![$T_j(x)=\cos[j\arccos(x)], x\in [-1,1]$](/articles/aa/full/2003/26/aa3477/img97.gif) .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... follows
![[*]](/icons/foot_motif.gif)
- In order to get m unknowns representing the
surface of the star in the
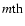 -order approximation discussed
in Sect. 3.3, we take the radii
-order approximation discussed
in Sect. 3.3, we take the radii
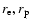 and (m-2) Chebyshev-coefficients for the
function g.
and (m-2) Chebyshev-coefficients for the
function g.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... surface
![[*]](/icons/foot_motif.gif)
- The continuity conditions of the fields' derivatives
will be part of the set of algebraic equations in question.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... functions
![[*]](/icons/foot_motif.gif)
-
Note that it is straightforward to calculate (i) the Chebyshev
coefficients of a function from its values at the gridpoints (sj,tk) (or
tk in the one-dimensional case), see Eq. (42), (ii) the value of a
function at an arbitrary point inside or at the boundary of I2 (or I)
from its Chebyshev coefficients, and (iii) the Chebyshev
coefficients of the derivative and the integral of a function from its Chebyshev
coefficients, see Press et al. (1992).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... reads
![[*]](/icons/foot_motif.gif)
-
Note that the function
HU'(m)(s=0,t) tends to a
constant in the limit
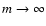 .
Similar properties hold for all functions listed in
(40), see also Sect. 3.6.
.
Similar properties hold for all functions listed in
(40), see also Sect. 3.6.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... respectively
![[*]](/icons/foot_motif.gif)
- For a description of the equations of
state corresponding to polytropic and strange star matter, see Tooper
(1965) and e.g. Gourgoulhon et al. (1999) respectively.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
body
![[*]](/icons/foot_motif.gif)
- The quantities M and
J can also be taken from the exterior fields
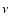 and
and 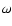 ,
see Eqs. (19).
,
see Eqs. (19).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
![[*]](/icons/foot_motif.gif)
- Note that the example listed in Table 5 has previously been
calculated, see Nozawa et al. (1998).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
stationarity
![[*]](/icons/foot_motif.gif)
- A locally stationary, axisymmetric spacetime requires the
existence of a timelike linear combination of the two Killing vectors
corresponding to stationarity and axisymmetry. The latter one vanishes on the
symmetry axis.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.