All the main ionic species are present in the echellograms, with the usual, dreadful handicap for hydrogen:
due to the large H![]() broadening, the deconvolution for
instrumental resolution plus thermal motions plus fine structure appears inadequate, and
the detailed F(H
broadening, the deconvolution for
instrumental resolution plus thermal motions plus fine structure appears inadequate, and
the detailed F(H
![]() profile cannot be determined. Moreover:
profile cannot be determined. Moreover:
- the principal O+ emissions
(![]() 3726
3726 ![]() and
and ![]() 3729 Å) fall outside our
spectral range. We have considered the much weaker
3729 Å) fall outside our
spectral range. We have considered the much weaker ![]() 7319.87 Å
the strongest line of the red O+ quartet;
7319.87 Å
the strongest line of the red O+ quartet;
- ![]() 3967 Å of [Ne III] being at the extreme blue edge
of the frame, the quantitative Ne++ analysis appears quite uncertain.
3967 Å of [Ne III] being at the extreme blue edge
of the frame, the quantitative Ne++ analysis appears quite uncertain.
In absence of H![]() we are forced to adopt
we are forced to adopt ![]() 5007 Å as reference line, thus
obtaining the radial ionization structure relative to O++ according to:
5007 Å as reference line, thus
obtaining the radial ionization structure relative to O++ according to:
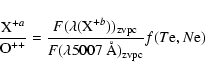 |
(3) |
The radial profiles of
![]() at the four selected PA of NGC 6818, shown in Fig. 6, contain
a number of interesting features:
at the four selected PA of NGC 6818, shown in Fig. 6, contain
a number of interesting features:
- the weakness of the low excitation emissions in PA
![]() northern sector, PA
northern sector, PA
![]() both sectors and
PA
both sectors and
PA
![]() both sectors indicates that the nebula is optically thin in these directions. It is almost thick in PA
both sectors indicates that the nebula is optically thin in these directions. It is almost thick in PA
![]() southern sector and PA
southern sector and PA
![]() both sectors;
both sectors;
- as expected, He++/O++ decreases outward and He+/ O++ increases. They cross for
![]() ,
implying that
,
implying that
![]() .
Since in these internal regions
.
Since in these internal regions
![]() (see Eqs. (10) and (11) in Sect. 6.3) we derive
(see Eqs. (10) and (11) in Sect. 6.3) we derive
![]() ;
;
- from similar considerations we infer
![]() ,
,
![]() ,
,
![]() and
and
![]() .
.
These chemical abundances (relative to oxygen) must be compared with the corresponding values (relative to hydrogen) obtained from the conventional method, as illustrated in the next Section.
According to the critical analysis by Alexander & Balick (1997) we consider the total line fluxes (i.e. integrated over the whole spatial profile and the expansion velocity field). The resulting ionic abundances must be multiplied for the corresponding ICFs, the correcting factors for the unobserved ionic stages. These were obtained both empirically (Barker 1983, 1986) and from interpolation of theoretical nebular models (Shields et al. 1981; Aller & Czyzak 1983; Aller 1984; Osterbrock 1989).
The final mean chemical abundances of NGC 6818, presented in Table 3 (last column), are in reasonable
agreement with the previous
estimates reported in the literature (also listed in the Table), and in excellent agreement with the
indications of Sect. 6.1.
![\begin{figure}
\par\includegraphics[width=15.1cm,clip]{H4002F6.eps}
\end{figure}](/articles/aa/full/2003/10/aah4002/Timg123.gif) |
Figure 6:
The radial ionization structure (relative to O++) at PA
|
As emphasized in Paper IV, the H![]() flux distribution in the zvpc,
F(H
flux distribution in the zvpc,
F(H![]() )
)
![]() ,
is the fundamental
parameter linking
,
is the fundamental
parameter linking ![]() with both the spatial and the
kinematical properties of the expanding plasma through the relation:
with both the spatial and the
kinematical properties of the expanding plasma through the relation:
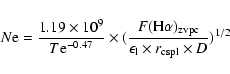 |
(4) |
In order to recover F(H![]() )
)
![]() we start assuming
we start assuming
![]() ,
constant across the nebula.
At each radial position:
,
constant across the nebula.
At each radial position:
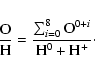 |
(5) |
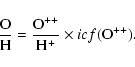 |
(6) |
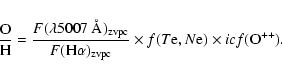 |
(7) |
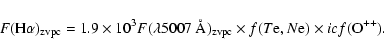 |
(8) |
Equation (8) provides the H![]() flux distribution in the zvpc (and
flux distribution in the zvpc (and
![]() (H
(H![]() )
through Eq. (4)) once the ionization correcting factor
)
through Eq. (4)) once the ionization correcting factor
![]() is known. The complex structure of NGC 6818 implies that
is known. The complex structure of NGC 6818 implies that
![]() strongly changes across the nebula. In the innermost
regions we have: O0/O++<<1, O+/O++<<1 and
H0/H+<<1. Thus
strongly changes across the nebula. In the innermost
regions we have: O0/O++<<1, O+/O++<<1 and
H0/H+<<1. Thus
![]() becomes:
becomes:
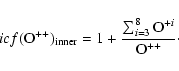 |
(9) |
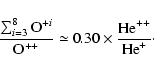 |
(10) |
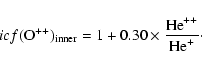 |
(11) |
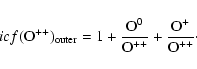 |
(12) |
Figure 7 evidences the basic advantage of using
![]() in the determination of the electron density
radial distribution:
in the determination of the electron density
radial distribution: ![]() (H
(H![]() )
extends
all over the nebular image, whereas
)
extends
all over the nebular image, whereas ![]() [S II] is limited to the peaks of the low excitation regions.
[S II] is limited to the peaks of the low excitation regions.
| Element | Aller & Czyzak | de Freitas Pacheco et al. | Liu & Danziger | Hyung et al. | This paper |
| (1983) | (1991) | (1993) | (1999) | ||
| He | 0.107 | 0.126 | 0.114 | 0.105 | 0.106( |
| C | 4.47 |
- | - | 8.0 |
- |
| N | 1.41 |
1.1 |
- | 4.0 |
1.4( |
| O | 5.50 |
5.25 |
6.37 |
7.0 |
5.5( |
| Ne | 1.23 |
- | - | 1.0 |
9.0( |
| Na | 3.09 |
- | - | 3.0 |
- |
| Mg | - | - | - | 3.0 |
- |
| Si | - | - | - | 9.0 |
- |
| S | 8.9 |
1.2 |
- | 7.0 |
6.2( |
| Cl | 1.9 |
- | - | 3.0 |
- |
| Ar | 3.8 |
- | - | 4.0 |
4.0( |
| K | 1.02 |
- | - | 2.0 |
- |
| Ca | 1.15 |
- | - | 1.5 |
- |
In detail:
- at PA
![]() (along the apparent major axis),
(along the apparent major axis), ![]() (H
(H![]() )
presents a single, broad and asymmetric (i.e. steeper
outwards) bell-shaped profile;
)
presents a single, broad and asymmetric (i.e. steeper
outwards) bell-shaped profile;
- the double-peak structure is very subtle at PA
![]() (close to the apparent major axis), the
inner peaks being predominant;
(close to the apparent major axis), the
inner peaks being predominant;
- at both PA
![]() and 110
and 110
![]() (close to the apparent minor axis) the two-shell
distribution clearly appears; the
(close to the apparent minor axis) the two-shell
distribution clearly appears; the ![]() (H
(H![]() )
top corresponds to the inner peaks at PA
)
top corresponds to the inner peaks at PA
![]() ,
whereas at
PA
,
whereas at
PA
![]() the peaks are almost equivalent;
the peaks are almost equivalent;
- an outward, low density tail is present at all directions, extending up to about 15 arcsec from the star.
Note in Fig. 7 the match between ![]() (H
(H![]() )
and
)
and ![]() [S II] for
[S II] for
![]() 9.5(
9.5(![]() 1) arcsec kpc, implying that
1) arcsec kpc, implying that
![]() ) kpc (see Table 2 and Sect. 4).
Although the assumption
) kpc (see Table 2 and Sect. 4).
Although the assumption
![]() provides a lower limit of 0.9 kpc
for the nebular distance, we can no longer delay a better quantification of this fundamental parameter.
provides a lower limit of 0.9 kpc
for the nebular distance, we can no longer delay a better quantification of this fundamental parameter.
Copyright ESO 2003