

Up: The 3-D ionization structure recombination
The only individual distance reported in the literature (based on rough parameters for the star and the nebula)
goes back to Gurzadyan (1970), who derived an indicative value of 2.2 kpc from the observed to expected size of
the He++ zone.
As compensation the nebula is present in a good 20 catalogues of statistical distances (listed in Table 4). They provide the
following mean values:
-
- <D>(Shklovsky)
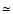 2.0(
2.0(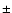 0.4) kpc;
0.4) kpc;
-
- <D>(ionized mass-radius relation)
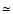 1.7(
1.7(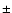 0.4) kpc;
0.4) kpc;
-
- <D>(surface brightness-radius relation)
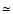 1.3(
1.3(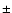 0.4) kpc;
0.4) kpc;
-
- <D>(other methods)
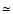 2.8(
2.8(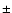 1.0) kpc.
1.0) kpc.
To be noticed that the overall properties inferred in the previous sections (in synthesis: NGC 6818 is an optically
thin, almost thin in some directions, quite "normal'' PN) suggest that <D>(Shklovsky),
<D>(ionized mass-radius relation) and <D>(surface brightness-radius relation) are, at least grossly, reliable.
In order to derive the dynamical parallax we have analysed the first
and second epoch (1998.30 and 2000.45, respectively) HST images of NGC
6818, searching for the angular expansion of the ionized gas; when
combined with Eq. (1), it provides a reliable nebular distance (Reed
et al. 1999; Palen et al. 2002). Since the target is at the centre of
the planetary camera (PC) chip in the 2000.45 images, whereas it is
quite off-axis in the 1998.30 ones, the correction for optical camera
distortions was performed with the IRAF/STSDAS task "drizzle'' (see
Fruchter & Hook 2002) using the Trauger coefficients.
No apparent shift is obtained from the couples of [O III] and [N II] frames.
According to Reed et al. (1999), we infer that the
angular expansion of the gas is <1.2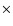 10-2 arcsec, that is
10-2 arcsec, that is
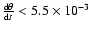 arcsec yr-1.
Since
arcsec yr-1.
Since
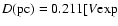 (km s-1)/
(km s-1)/
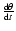 (arcsec yr-1)], we derive
(arcsec yr-1)], we derive
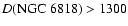 pc.
pc.
We have attempted a better quantification of D(NGC 6818) through the
interstellar absorption-distance relation (Lutz 1973; Gathier et al. 1986;
Saurer 1995) given by the field stars with accurate mV,
mB, spectral type and luminosity class. They were selected using
the SIMBAD facilities of the CDS, Strasbourg Astronomical Observatory.
The resulting 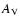 -distance law is presented in Fig. 8, where the small cluster of data at the right
edge refers to the super-giant stars of NGC 6822 (Barnard's galaxy), a nearby Ir galaxy projected at about 40
arcmin S-SE of our nebula.
-distance law is presented in Fig. 8, where the small cluster of data at the right
edge refers to the super-giant stars of NGC 6822 (Barnard's galaxy), a nearby Ir galaxy projected at about 40
arcmin S-SE of our nebula.
Figure 8 indicates that:
- the galactic absorption rapidly changes in direction (note the spread of the
low-weight points). This is confirmed by the inspection of both the ESO/SERC and the Palomar
Schmidt surveys, showing a variable background crossed by a series of extended, broad and faint emitting filaments;
- close to the nebula direction (high-weight data), 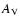 quickly increases up to
quickly increases up to
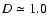 -1.5 kpc,
and later is constant (as expected of the large galactic latitude of the field,
-1.5 kpc,
and later is constant (as expected of the large galactic latitude of the field,
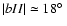 ). Note that
for the super-giant stars of the nearby galaxy NGC 6822 we have
). Note that
for the super-giant stars of the nearby galaxy NGC 6822 we have
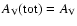 (galactic)
(galactic)
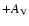 (NGC 6822), where
(NGC 6822), where
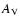 (NGC 6822) changes from star to star, and
(NGC 6822) changes from star to star, and 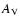 (galactic) = const. For
(galactic) = const. For 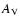 (NGC 6822) = 0 we infer
(NGC 6822) = 0 we infer
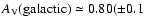 ), in excellent agreement with the literature reports (see Gallart et al. 1996; Bianchi et al. 2001);
), in excellent agreement with the literature reports (see Gallart et al. 1996; Bianchi et al. 2001);
- from
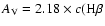 )
(Acker 1978) we have
)
(Acker 1978) we have
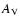
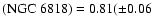 )
and D(NGC 6818)
)
and D(NGC 6818)
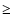 1.5 kpc.
1.5 kpc.
Although in Fig. 8 all the solutions for
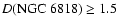 kpc appear legitimate, both the large galactic latitude
of the nebula (
kpc appear legitimate, both the large galactic latitude
of the nebula (
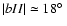 )
and the low radial velocity relative to the Local Standard of Rest,
)
and the low radial velocity relative to the Local Standard of Rest,
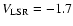 km s-1 (Sect. 4),
decidedly favour the lowest values, i.e.
km s-1 (Sect. 4),
decidedly favour the lowest values, i.e.
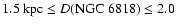 kpc (in agreement with the information
previously obtained from the statistical distance scales).
kpc (in agreement with the information
previously obtained from the statistical distance scales).
In the following we will adopt
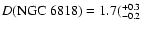 ) kpc,
corresponding to a distance from the galactic plane
) kpc,
corresponding to a distance from the galactic plane 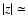 0.5 kpc.
0.5 kpc.
The local filling factor in the nebula is
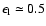 .
The ionized mass (obtained in different ways: from the H
.
The ionized mass (obtained in different ways: from the H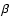 flux, the radio flux and the observed
flux, the radio flux and the observed 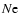 distribution;
Aller 1984; Pottasch 1984; Osterbrock 1989 and
Paper IV) results to be
distribution;
Aller 1984; Pottasch 1984; Osterbrock 1989 and
Paper IV) results to be
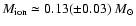 ,
and the kinematical age
,
and the kinematical age
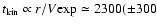 ) yr.
) yr.
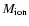 is close to the total nebular mass, NGC 6818 being an optically thin (almost thin in
some directions) PN, whereas
is close to the total nebular mass, NGC 6818 being an optically thin (almost thin in
some directions) PN, whereas
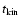 represents a lower limit to the actual age,
represents a lower limit to the actual age,
 ,
since the dynamical history of the gas is unknown.
We can obtain a reliable estimate of
,
since the dynamical history of the gas is unknown.
We can obtain a reliable estimate of
 by assuming a nebular ejection at
by assuming a nebular ejection at
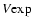
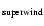
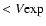
 ,
followed by a constant acceleration up to
,
followed by a constant acceleration up to
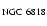 .
.
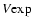
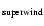 comes from the OH/IR sources, commonly regarded as the PNe precursors
(Habing 1996). For
comes from the OH/IR sources, commonly regarded as the PNe precursors
(Habing 1996). For
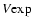
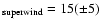 km s-1 (Chengalur et al. 1993; David et al. 1993; Sjouwerman et al. 1998) we derive
km s-1 (Chengalur et al. 1993; David et al. 1993; Sjouwerman et al. 1998) we derive
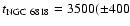 ) yr, i.e. our nebula is rather young.
) yr, i.e. our nebula is rather young.


Up: The 3-D ionization structure recombination
Copyright ESO 2003