We can obtain the ![]() radial profile from the diagnostic line ratios
of ions in p2 or p4 configurations (like [O III] and [N II]), and the
radial profile from the diagnostic line ratios
of ions in p2 or p4 configurations (like [O III] and [N II]), and the ![]() radial distribution from both
the diagnostics of ions in p3 configuration (like [S II]) and the absolute H
radial distribution from both
the diagnostics of ions in p3 configuration (like [S II]) and the absolute H![]() flux. According to
Paper IV, the zvpc, which is independent on the expansion velocity field, must be used.
flux. According to
Paper IV, the zvpc, which is independent on the expansion velocity field, must be used.
In the specific case of NGC 6818 the large H![]() broadening
(due to thermal motions, fine structure and expansion velocity gradient) prevents the accurate determination of
F(H
broadening
(due to thermal motions, fine structure and expansion velocity gradient) prevents the accurate determination of
F(H![]() )
)
![]() (and then of
(and then of ![]() (H
(H![]() )).
Thus, in this section
)).
Thus, in this section ![]() [O III],
[O III], ![]() [N II] and
[N II] and ![]() [S II] are derived from the corresponding line intensity
ratios. Later on (Sect. 6.3) we will illustrate the adopted escamotage providing
F(H
[S II] are derived from the corresponding line intensity
ratios. Later on (Sect. 6.3) we will illustrate the adopted escamotage providing
F(H![]() )
)
![]() and
and ![]() (H
(H![]() )
from the observed radial ionization structure and the assumption
)
from the observed radial ionization structure and the assumption ![]() constant across the nebula.
constant across the nebula.
First of all the observed line intensities must be corrected for interstellar absorption according
to:
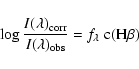 |
(2) |
Thanks to the excellent spatial and spectral accuracies achieved by the
superposition technique used (![]() 0.15 arcsec and
0.15 arcsec and ![]() 1.0 km s-1,
respectively) we can extend the H
1.0 km s-1,
respectively) we can extend the H![]() /H
/H![]() analysis to
the whole spectral image, as recently introduced (Paper IV) in the study of
NGC 6565, a compact, dust embedded PN exhibiting a complex c(H
analysis to
the whole spectral image, as recently introduced (Paper IV) in the study of
NGC 6565, a compact, dust embedded PN exhibiting a complex c(H![]() )
profile.
The results are less dramatic for NGC 6818, since the blurred appearance of both H
)
profile.
The results are less dramatic for NGC 6818, since the blurred appearance of both H![]() and H
and H![]() limits the resolution: besides some indications of a soft decline in the innermost regions (likely caused
by a local increase of
limits the resolution: besides some indications of a soft decline in the innermost regions (likely caused
by a local increase of ![]() ), the spectral maps appear quite homogeneous at
), the spectral maps appear quite homogeneous at
![]() ),
corresponding to
),
corresponding to
![]() )
(for the case B of Baker & Menzel 1938,
)
(for the case B of Baker & Menzel 1938,
![]() K and
log
K and
log
![]() ;
Brocklehurst 1971; Aller 1984; Hummer & Storey 1987).
;
Brocklehurst 1971; Aller 1984; Hummer & Storey 1987).
First we obtain ![]() [O III] from
[O III] from ![]() 5007 Å/
5007 Å/![]() 4363 Å, the line ratio being almost
independent on
4363 Å, the line ratio being almost
independent on ![]() for
for
![]() cm-3.
cm-3.
![]() [S II] is then derived from
[S II] is then derived from ![]() 6717 Å/
6717 Å/![]() 6731 Å (using
6731 Å (using ![]() [O III] to take into
account the weak dependence of the ratio on
[O III] to take into
account the weak dependence of the ratio on ![]() ).
Last,
).
Last, ![]() [N II] comes from
[N II] comes from ![]() 6584 Å/
6584 Å/![]() 5755 Å (adopting
5755 Å (adopting ![]() [S II] for its weak dependence
on the electron density).
[S II] for its weak dependence
on the electron density).
Although the resulting ![]() [O III],
[O III], ![]() [N II] and
[N II] and ![]() [S II] profiles rapidly change with PA,
as expected of the chaotic structure of NGC 6818, nevertheless there are some common features.
In order to highlight both the differences and the analogies we have selected two PA close to the apparent
major axis (PA
[S II] profiles rapidly change with PA,
as expected of the chaotic structure of NGC 6818, nevertheless there are some common features.
In order to highlight both the differences and the analogies we have selected two PA close to the apparent
major axis (PA
![]() and PA
and PA
![]() )
and two PA close to the apparent minor axis
(PA
)
and two PA close to the apparent minor axis
(PA
![]() and PA
and PA
![]() )
as representative of the whole nebular phenomenology.
)
as representative of the whole nebular phenomenology.
The results are shown in Fig. 5; their main limitation is evident: due to the weakness of the [N II] auroral
line and of the [S II] doublet, ![]() [N II] and
[N II] and ![]() [S II] can be obtained only at the
corresponding intensity peaks (in the best case).
[S II] can be obtained only at the
corresponding intensity peaks (in the best case).
![]() [O III] presents a well-defined radial profile common to all the PA: it is
[O III] presents a well-defined radial profile common to all the PA: it is ![]() 15 000 K in the
tenuous, innermost regions, it gradually decreases outward down to 12 000-12 500 K in the densest layers, and
later it remains more or less constant (the last statement is weakened by the auroral line faintness). Such a radial
trend is in quantitative agreement with the results by Rubin et al. (1998), based on
15 000 K in the
tenuous, innermost regions, it gradually decreases outward down to 12 000-12 500 K in the densest layers, and
later it remains more or less constant (the last statement is weakened by the auroral line faintness). Such a radial
trend is in quantitative agreement with the results by Rubin et al. (1998), based on ![]() 4363 Å
and
4363 Å
and ![]() 5007 Å HST/WFPC2 imagery. The presence of a
5007 Å HST/WFPC2 imagery. The presence of a ![]() gradient across
the nebula is also suggested by Hyung et al. (1999). Previous ground-based
gradient across
the nebula is also suggested by Hyung et al. (1999). Previous ground-based ![]() [O III] determinations are mean values
for the brightest (i.e. densest) regions and span the range 11400 K (de Freitas Pacheco et al.
1991) to
12 770 K (Mathis et al. 1998).
[O III] determinations are mean values
for the brightest (i.e. densest) regions and span the range 11400 K (de Freitas Pacheco et al.
1991) to
12 770 K (Mathis et al. 1998).
In Fig. 5 ![]() [N II] refers to the intensity peaks of the low ionization regions and is systematically below
[N II] refers to the intensity peaks of the low ionization regions and is systematically below ![]() [O III],
in agreement with both the previous reports for NGC 6818 (9500 K, Hyung et al. 1999, to 11 280 K, McKenna et al. 1996)
and the general results for PNe (see Aller 1990; Gruenwald & Viegas 1995; Mathis et al. 1998).
More
[O III],
in agreement with both the previous reports for NGC 6818 (9500 K, Hyung et al. 1999, to 11 280 K, McKenna et al. 1996)
and the general results for PNe (see Aller 1990; Gruenwald & Viegas 1995; Mathis et al. 1998).
More ![]() values for NGC 6818 are: 11 500 K (C III], Kaler 1986), 12 700 K and 13 800 K ([Ne V] and [O IV],
respectively, Rowlands et al. 1989), 14 700 K (Balmer discontinuity, Liu & Danziger 1993), 12 500 K (C III], Mathis et al. 1998), 13 000 K ([Cl IV], Hyung et al. 1999) and 19 000 K ([O II], Keenan et al. 1999).
values for NGC 6818 are: 11 500 K (C III], Kaler 1986), 12 700 K and 13 800 K ([Ne V] and [O IV],
respectively, Rowlands et al. 1989), 14 700 K (Balmer discontinuity, Liu & Danziger 1993), 12 500 K (C III], Mathis et al. 1998), 13 000 K ([Cl IV], Hyung et al. 1999) and 19 000 K ([O II], Keenan et al. 1999).
In summary, the mean kinetic energy of the free electrons in NGC 6818 is quite large. This on the one hand
explains both the H![]() broadening and the strength of the forbidden lines (in particular,
broadening and the strength of the forbidden lines (in particular,
![]() 5007 Å of
[O III]), on the other hand is indicative of a very hot central star
(
5007 Å of
[O III]), on the other hand is indicative of a very hot central star
(
![]() K, also supported by the presence of high excitation emissions, up to [Ne V],
IP =97.1 eV; see Table 1).
K, also supported by the presence of high excitation emissions, up to [Ne V],
IP =97.1 eV; see Table 1).
Concerning the [S II] electron densities in the zvpc (Fig. 5), they are limited to the brightest parts of the external,
low ionization layers and show peaks up to
![]() ) cm-3.
Previously Hyung et al. (1999) obtained
) cm-3.
Previously Hyung et al. (1999) obtained
![]() cm-3 (they also report
cm-3 (they also report
![]() cm-3 from the improved calculations for 3 equivalent p-electrons by Keenan et al. 1996).
cm-3 from the improved calculations for 3 equivalent p-electrons by Keenan et al. 1996).
Besides the zvpc, we have extended the ![]() 6717 Å/
6717 Å/![]() 6731 Å analysis to the prominent
knots of the entire [S II] spectral images. The resulting
6731 Å analysis to the prominent
knots of the entire [S II] spectral images. The resulting ![]() [S II] values span the range
[S II] values span the range
![]() )
to
)
to
![]() ) cm-3, the equatorial moustaches being the densest regions of NGC 6818.
) cm-3, the equatorial moustaches being the densest regions of NGC 6818.
In the next section we will derive the local filling factor,
![]() ,
by combining
,
by combining ![]() [S II] and
[S II] and ![]() (H
(H
![]() ,
since
,
since ![]() [S II]
[S II]![]()
![]() (H
(H
![]() (Aller 1984;
Osterbrock 1989).
(Aller 1984;
Osterbrock 1989).
Copyright ESO 2003