

Up: On the accretion luminosity
Although the interchange instabilities of the magnetospheric
boundary during the subsonic propeller state are suppressed, the
"magnetic gates'' are not closed completely: the atmospheric plasma
is able to penetrate into the stellar magnetic field due to
diffusion. The diffusion rate is limited to (see e.g. Ikhsanov
2001b)
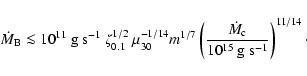 |
(10) |
Here
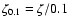 is the diffusion efficiency, which is
normalized following the results of experiments on the nuclear
fusion (e.g. Hamasaki et al.1974) and the measurements of the
solar wind penetrating the magnetosphere of the Earth (Gosling et al.
1991).
is the diffusion efficiency, which is
normalized following the results of experiments on the nuclear
fusion (e.g. Hamasaki et al.1974) and the measurements of the
solar wind penetrating the magnetosphere of the Earth (Gosling et al.
1991).
This means that the hot atmosphere surrounding the magnetosphere
of the star in the subsonic propeller state cannot be purely
stationary. For the atmosphere to remain in an equilibrium state,
the amount of material flowing from its base into the
magnetosphere must be compensated for by the same amount of
material coming into the atmosphere through its outer boundary.
Thus the radial drift of plasma through the atmosphere with the
rate
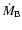 and the velocity
and the velocity
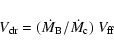 |
(11) |
towards the neutron star is expected.
The structure of the atmosphere with the radial plasma drift can
be explain in terms of the quasi-stationary model of Davies &
Pringle (1981) as long as the characteristic time of the
accretion process,
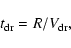 |
(12) |
is larger than the characteristic time of turbulent motions
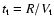 .
According to Davies & Pringle
(1981), the velocity of turbulence motions can be
approximated as
.
According to Davies & Pringle
(1981), the velocity of turbulence motions can be
approximated as
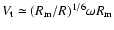 .
Therefore, the condition
.
Therefore, the condition
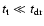 proves to be satisfied if the spin period of the star is
proves to be satisfied if the spin period of the star is
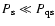 ,
where
,
where
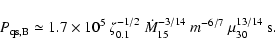 |
(13) |
Thus, as long as the spin period of the star is
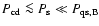 ,
the magnetosphere of the star is
surrounded by a hot (
,
the magnetosphere of the star is
surrounded by a hot (
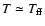 )
atmosphere in which
the plasma pressure is
)
atmosphere in which
the plasma pressure is
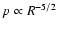 ,
the sound speed is
,
the sound speed is
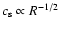 and the number density is
and the number density is
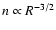 (for discussion see Davies & Pringle 1981).
(for discussion see Davies & Pringle 1981).
The radial drift of plasma through the atmosphere towards the
neutron star leads to the release of the accretion (potential)
energy, which is mainly spent in heating the atmospheric plasma.
The heating rate due to this process is
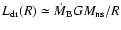 .
This value is small in comparison
with that of the spin-down power (see Davies & Pringle
1981, Eq. (3.2.4)),
.
This value is small in comparison
with that of the spin-down power (see Davies & Pringle
1981, Eq. (3.2.4)),
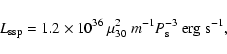 |
(14) |
as long as the spin period of the star is
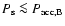 ,
where
,
where
 |
(15) |
However, under the condition
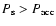 the heating
of the atmospheric plasma is governed by the accretion power.
the heating
of the atmospheric plasma is governed by the accretion power.
The characteristic time of the heating due to accretion process is
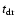 .
On the other hand, the cooling time of the
atmospheric plasma due to the bremsstrahlung emission is
.
On the other hand, the cooling time of the
atmospheric plasma due to the bremsstrahlung emission is
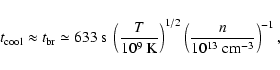 |
(16) |
where n is the number density of the atmospheric plasma, which
can be expressed as
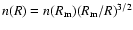 ,
where
,
where
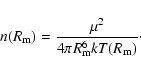 |
(17) |
Hence, for the temperature of the atmospheric plasma to be smaller
than the critical value,
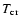 ,
the following condition
should be satisfied
,
the following condition
should be satisfied
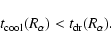 |
(18) |
I require this condition to be satisfied at the outer boundary of
the atmosphere since
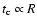 and
and
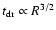 .
Combining Eqs. (11), (12), (16),
and (17), one finds that the bremsstrahlung cooling
dominates the heating due to accretion power only if the strength
of the stellar wind is
.
Combining Eqs. (11), (12), (16),
and (17), one finds that the bremsstrahlung cooling
dominates the heating due to accretion power only if the strength
of the stellar wind is
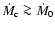 ,
where
,
where
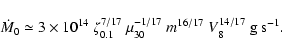 |
(19) |
This means that a magnetized isolated neutron star is able to
switch its state from subsonic propeller to steady
accretor only if the mass capture rate by this star from the
interstellar medium is
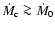 .
Otherwise,
the corresponding state transition does not occur and the star
remains surrounded by the hot atmosphere. In this case the mass
accretion rate onto the stellar surface is limited to
.
Otherwise,
the corresponding state transition does not occur and the star
remains surrounded by the hot atmosphere. In this case the mass
accretion rate onto the stellar surface is limited to
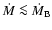 (see Eq. (10)) and, correspondingly, the
accretion luminosity is
(see Eq. (10)) and, correspondingly, the
accretion luminosity is
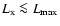 ,
where
,
where
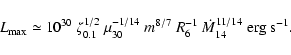 |
(20) |
Here R6 is the radius of the neutron star expressed in units of 106 cm, and
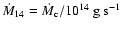 .
.


Up: On the accretion luminosity
Copyright ESO 2003
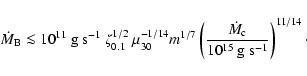
![]() and the velocity
and the velocity
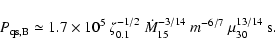
![]() .
This value is small in comparison
with that of the spin-down power (see Davies & Pringle
1981, Eq. (3.2.4)),
.
This value is small in comparison
with that of the spin-down power (see Davies & Pringle
1981, Eq. (3.2.4)),
![]() .
On the other hand, the cooling time of the
atmospheric plasma due to the bremsstrahlung emission is
.
On the other hand, the cooling time of the
atmospheric plasma due to the bremsstrahlung emission is