Application of our findings to the case of INSs leads to the
following conclusions. First, comparing Eqs. (4) and
(19) one finds that under the conditions of interest the
maximum possible strength of the stellar wind of an isolated
neutron star,
![]() ,
is smaller (at least by a
factor of 3) than
,
is smaller (at least by a
factor of 3) than ![]() .
Therefore, the interchange
instabilities of the magnetospheric boundary of these stars are
suppressed and the plasma penetration from the base of the hot
atmosphere into the stellar magnetic field is governed by the Bohm
diffusion. In this case the accretion luminosity of INSs, whose
age is smaller than the characteristic time of the magnetic field
decay,
.
Therefore, the interchange
instabilities of the magnetospheric boundary of these stars are
suppressed and the plasma penetration from the base of the hot
atmosphere into the stellar magnetic field is governed by the Bohm
diffusion. In this case the accretion luminosity of INSs, whose
age is smaller than the characteristic time of the magnetic field
decay,
![]() ,
is limited to
,
is limited to
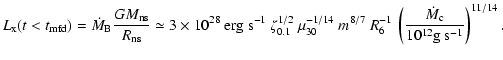 |
(21) |
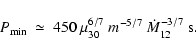 |
(22) |
Finally, for
![]() ,
the
spin-down time scale of a neutron star in the subsonic propeller
state is (see Davies & Pringle 1981, Eq. (3.2.5))
,
the
spin-down time scale of a neutron star in the subsonic propeller
state is (see Davies & Pringle 1981, Eq. (3.2.5))
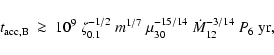 |
(23) |
Acknowledgements
I would like to thank the referee, Dr. Marina Romanova, for useful comments and suggested improvements. I acknowledge the support of the Alexander von Humboldt Foundation within the Long-term Cooperation Program.
Copyright ESO 2003