2 Evolutionary tracks of INSs

As was first recognized by Shvartsman (1970), the evolutionary track of a rotating magnetized neutron star can be presented in the form of the following sequence of its states: ejector $\rightarrow$ propeller $\rightarrow$ accretor. Within this scheme, the rotational rate of a newly born fast rotating neutron star decreases, initially by the generation of the magneto-dipole waves and ejection of relativistic particles (pulsar-like spin-down), and later by means of the interaction between its magnetosphere and the surrounding material (propeller spin-down). The first state transition occurs when the pressure of the material ejected by the star can no longer balance the pressure of the surrounding gas, and the latter, penetrating into the accretion radius of the star, interacts with the stellar magnetosphere. A detailed analysis of this state transition with respect to INSs was presented by Popov et al. (2000b).

The spin evolution of a spherically accreting strongly magnetized neutron star in the state of propeller has been investigated by Davies et al. (1979) and Davies & Pringle (1981). As they shown, two sub-states of the propeller state can be distinguished: the supersonic and subsonic propeller. In both cases the neutron star is spinning down due to the interaction between its magnetosphere and the surrounding gas. As a result of this interaction, the star's magnetosphere is surrounded by a spherical quasi-static atmosphere, in which the plasma temperature is of the order of the free-fall temperature

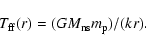$$% T_{\rm ff}(r)=(GM_{\rm ns} m_{\rm p})/(k r).$$ (5)

Here G, $m_{\rm p}$, and k are the gravitational constant, the proton mass, and the Boltzmann constant, respectively.

The atmosphere is extended from the magnetospheric boundary up to the accretion radius of the neutron star. The rotational energy loss by the neutron star is convected up through the atmosphere by the turbulent motion and lost through its outer boundary.

The formation of the atmosphere in the first approximation prevents the surrounding gas from penetrating to within the accretion radius of the star. As the neutron star moves through the interstellar medium, the interstellar gas overflows the outer edge of the atmosphere with the rate $\dot{M}_{\rm c}$ (see Eq. (2)), which is traditionally called the strength of the stellar wind and denotes the maximum possible mass capture rate by the neutron star.

2.1 Supersonic propeller

As long as the angular velocity of the neutron star is large enough for the corotational radius to be smaller than the magnetospheric radius, the star is in the centrifugal inhibition regime (i.e. the centrifugal acceleration at the magnetospheric boundary, $\omega^2 R_{\rm m}$, dominates the gravitational acceleration, $GM_{\rm ns}/R_{\rm m}^2$). The centrifugal inhibition is not effective only within the bases of the corotational cylinder. However, the accretion of material onto the stellar surface through these regions does occur only if the the angle between the magnetic and rotational axes is small enough (see Ikhsanov 2001c) and if the magnetic field of the star is weak enough for the magnetospheric radius to exceed the stellar radius only by a factor of 2-3 (for discussion see Toropin et al. 1999; Romanova et al. 2002). Otherwise, the accretion power is significantly smaller than the spin-down power due to propeller action by the fast rotating star.

Except the bases of the corotational cylinder, the linear velocity at the boundary of the magnetosphere, which is co-rotating with the star, in this case is larger than the sound speed in the atmospheric plasma. That is why this state is usually refereed to as a supersonic propeller (see also Ikhsanov 2002).

2.2 Subsonic propeller

As the star is spinning down, its corotational radius increases and reaches the magnetospheric radius when $P_{\rm s} = P_{\rm cd}$, where

$$% P_{\rm cd} \simeq 23\ \mu_{30}^{6/7}\ m^{-5/7}\ \dot{M}_{15}^{-3/7}\ {\rm s}.$$ (6)

Here $\dot{M}_{15}$ is the strength of the stellar wind expressed in units of  $10^{15}~{\rm g~s^{-1}}$, and $\mu_{30}$ is the dipole magnetic moment of a neutron star expressed in units of $10^{30}~{\rm G~cm^3}$.

Under the condition $P_{\rm s} > P_{\rm cd}$ the centrifugal barrier is not effective: the atmospheric plasma, penetrating into the magnetic field of the star, is able to flow along the magnetic field lines and to accrete onto the stellar surface. However, as shown by Arons & Lea (1976) and Elsner & Lamb (1976), the rate of plasma penetration into the magnetosphere of a spherically accreting strongly magnetized neutron star can be as high as $\dot{M}_{\rm c}$ only if the magnetospheric boundary is unstable with respect to interchange (e.g. Rayleigh-Taylor) instabilities. Otherwise, the rate of plasma penetration is limited to the diffusion rate, which is a few orders of magnitude smaller than $\dot{M}_{\rm c}$ (see Eq. (10)). For instability to occur the sign of the effective gravitational acceleration at the magnetospheric boundary should be positive:

$$% g_{\rm eff}\ = \frac{G M_{\rm ns}}{R_{\rm m}^{2}(\theta)} \... ...{V_{\rm T_{\rm i}}^{2}(R_{\rm m})}{R_{\rm curv}(\theta)} > 0.$$ (7)

Here $R_{\rm curv}$ is the curvature radius of the field lines, $\theta$ is the angle between the radius vector and the outward normal to the magnetospheric boundary and $V_{\rm T_{\rm i}}(R_{\rm m})$ is the ion thermal velocity of the accreting plasma at the boundary. For the case of the equilibrium magnetospheric shape derived by Arons & Lea (1976), the condition (7) can be expressed in terms of the plasma temperature at the magnetospheric boundary as

$$% T < T_{\rm cr} \simeq 0.3\ T_{\rm ff}.$$ (8)

This indicates that the condition $R_{\rm m} < R_{\rm cor}$ is necessary, but not sufficient for the effective accretion (with the rate of $\sim$ $\dot{M}_{\rm c}$) onto the surface of neutron star to start. In addition, it is required that the cooling of plasma at the base of the atmosphere is more effective than the heating.

As shown by Davies & Pringle (1981), the cooling of the atmospheric plasma is governed by the bremsstrahlung radiation and the convective motion. For these processes to dominate the energy input into the atmosphere due to the propeller action by the star, the spin period of the star should be $P_{\rm s} \ga P_{\rm br}$, where  $P_{\rm br}$ is a so-called break period, which according to Ikhsanov (2001a) is

$$% P_{\rm br} \simeq\ 450\ \mu_{30}^{16/21}\ \dot{M}_{15}^{-5/7}\ m^{-4/21}\ {\rm s}.$$ (9)

Under the conditions of interest, the break period significantly exceeds $P_{\rm cd}$. This means that the state transition supersonic propeller $\rightarrow$ steady accretor may occur only via an additional intermediate state, which is called the subsonic propeller. This term reflects the fact that the rotation velocity of the magnetosphere during this stage is smaller than the thermal velocity in the surrounding gas.

If the propeller action were the only source of heating of the atmospheric plasma, the magnetospheric boundary of the neutron star would be able to switch its state from subsonic propeller to accretor as its spin period reaches $P_{\rm br}$. However, as shown below, an additional heating of the atmospheric plasma occurs due to a radial plasma drift through the atmosphere. This additional heating mechanism turns out to be not effective if a star is situated in a relatively strong stellar wind, but in the opposite case it must be taken into account.