This case corresponds to
![]() .
We can introduce a
vector
.
We can introduce a
vector
![]() ,
which is proportional to the position vector
,
which is proportional to the position vector
![]() connecting the point
A(x0,y0,z0) (the centre of our
local frame) with the Z-axis in a z=z0 plane. Its absolute
value is equal to
connecting the point
A(x0,y0,z0) (the centre of our
local frame) with the Z-axis in a z=z0 plane. Its absolute
value is equal to
![]() .
The wave number dynamics is given by
simple linear solutions:
ki(t)=ki(0)-Cikzt, with i=x, y,
while the vertical component kz stays constant. The symmetry
of the flow implies that the vector product of
.
The wave number dynamics is given by
simple linear solutions:
ki(t)=ki(0)-Cikzt, with i=x, y,
while the vertical component kz stays constant. The symmetry
of the flow implies that the vector product of ![]() and
and
![]() has a constant vertical component
has a constant vertical component
![]() ,
which,
in its turn, is a linear combination of transverse components of
the wave number vector. This fact suggests the decomposition
,
which,
in its turn, is a linear combination of transverse components of
the wave number vector. This fact suggests the decomposition
![]() ,
,
![]() ,
i.e.,
,
i.e.,
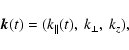 |
(20) |
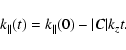 |
(21) |
| (22a) | |||
| (22b) | |||
| B(1)=-kzV, | (23a) | ||
| (23b) |
These variables give complete description of the system, because
"physical"
variables ![]() and
and ![]() are readily expressed by means of V,
are readily expressed by means of V,
![]() ,
B, and
,
B, and ![]() via the following vector identities:
via the following vector identities:
![$\displaystyle {\vec v}={1 \over{\vert{\vec C}{\times}{\vec k}\vert^2}}{\biggl[{...
...vec C}{\times}
{\vec k})+V({\vec k}{\times}({\vec C}{\times}{\vec k}))\biggr]},$](/articles/aa/full/2003/08/aah3329/img109.gif) |
(24a) | ||
![$\displaystyle {\vec b}={1 \over{\vert{\vec C}{\times}{\vec k}\vert^2}}{\biggl[{...
...vec C}{\times}
{\vec k})+B({\vec k}{\times}({\vec C}{\times}{\vec k}))\biggr]}.$](/articles/aa/full/2003/08/aah3329/img110.gif) |
(24b) |
![$\displaystyle E_{\rm k}={1 \over 2}\vert{\vec
v}\vert^2={1 \over{2\vert{\vec C}{\times}{\vec k}\vert^2}} {\biggl[{\cal
V}^2+V^2\vert{\vec k}\vert^2\biggr]},$](/articles/aa/full/2003/08/aah3329/img111.gif) |
(25a) | ||
![$\displaystyle E_{\rm m}={C_{\rm A}^2 \over
2}\vert{\vec b}\vert^2={C_{\rm A}^2 ...
...C}{\times} {\vec
k}\vert^2}}{\biggl[{\cal B}^2+B^2\vert{\vec k}\vert^2\biggr]},$](/articles/aa/full/2003/08/aah3329/img112.gif) |
(25b) | ||
| (25c) |
| (26) |
| (27) |
![$\displaystyle {\Psi}^{(2)}+{\biggl[{\omega}_{\rm A}^2-{{k_z^2\vert{\vec C}{\times}{\vec
k}\vert^2} \over{\vert{\vec k}\vert^4}}\biggr]}{\Psi}=0.$](/articles/aa/full/2003/08/aah3329/img119.gif) |
(28) |
| (29) |
| (30) |
![$\displaystyle {{{\rm d}^2{\Psi}}\over{{\rm d}T^2}}+{\biggl[1-{{a^2}\over{{\left(a^2+T^2
\right)}^2}} \biggr]}{\Psi}=0.$](/articles/aa/full/2003/08/aah3329/img122.gif) |
(31) |
![\begin{figure}
\par\includegraphics[angle=90,width=8cm,clip]{plot1.ps}\end{figure}](/articles/aa/full/2003/08/aah3329/Timg128.gif) |
Figure 1:
The plots of the function
|
Analysis of (31) begins by studying the temporal behavior of the
"effective frequency"
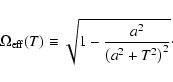 |
(32) |
Quantitative picture of this behavior is illustrated by Fig. 1
where we plotted the
![]() for different
(but all |a|<1) values of a. One sees that with the decrease
of a the minimum of
for different
(but all |a|<1) values of a. One sees that with the decrease
of a the minimum of
![]() becomes sharper:
the depth of the minimum in Fig. 1 (which accounts for maximum
increments of the transient instability) steadily increases with
the decreasing a. The width of the time interval, in which this
function stays negative (and, correspondingly,
becomes sharper:
the depth of the minimum in Fig. 1 (which accounts for maximum
increments of the transient instability) steadily increases with
the decreasing a. The width of the time interval, in which this
function stays negative (and, correspondingly,
![]() is imaginary) is maximum for a=1/2 and tends to zero
when
is imaginary) is maximum for a=1/2 and tends to zero
when ![]() and
and ![]() .
.
At a first glance, from (31), it seems that decreasing a we would have the continuous increase of the transient amplification rate. However decreasing a we also make smaller the scaling factor between the physical time t and the variable T, which appears in (31). Besides, the small values of a imply smaller values of the Alfvén speed and the vertical component of the wavenumber vector kz. Therefore, we can conclude that transient amplification factor for lower frequency Alfvén waves is higher, but for the amplification to occur the system needs a longer time interval. This means, in turn, that outflows with shorter/longer lifetime values are expected to amplify higher/lower frequency Alfvén waves.
![\begin{figure}
\par\includegraphics[angle=90,width=8.1cm,clip]{plot2.ps}\end{figure}](/articles/aa/full/2003/08/aah3329/Timg136.gif) |
Figure 2:
The numerical solution of Eq. (31) featuring the function
|
![\begin{figure}
\par\includegraphics[angle=90,width=8.1cm,clip]{plot3.ps} \end{figure}](/articles/aa/full/2003/08/aah3329/Timg139.gif) |
Figure 3:
The numerical solution of Eq. (31), which is
inversion-symmetric to the one given in Fig. 2. Initial values here
are:
|
The presence of the imaginary effective frequency for a limited
time interval means that Alfvén waves excited and maintained by
the shear flow become subject to a certain, velocity shear
induced instability, which is present only within the limited time
interval. That is why we specify this phenomenon by the term "transient instability". Since the time interval is rather brief
one can expect that the appearance of this instability will have a
burst-like, explosive nature: initially at times T < T- waves
stay almost unaffected by the presence of the shear flow. However,
as soon as the system will enter the transient instability
interval
T-<T< T+, the Alfvén waves undergo drastic and
abrupt change in their amplitudes. Depending on the initial
values, the mode of evolution will be a certain mixture of
swiftly decaying and/or increasing modes within the ![]() instability domain. But as soon as T > T+ the waves become
stable again and their amplitudes do not change anymore The
resulting wave amplitude is enhanced/diminished in comparison with
the initial amplitude depending whether transiently
increasing/decreasing component was dominant for the initially
excited wave.
instability domain. But as soon as T > T+ the waves become
stable again and their amplitudes do not change anymore The
resulting wave amplitude is enhanced/diminished in comparison with
the initial amplitude depending whether transiently
increasing/decreasing component was dominant for the initially
excited wave.
Numerical results, represented by Figs. 2-5, fully confirm these
qualitative expectations. Figures 2 and 3 illustrate the inversion
symmetry of the functions
![]() .
The first of these two
plots shows the temporal evolution for a=0.1 and with initial
conditions
.
The first of these two
plots shows the temporal evolution for a=0.1 and with initial
conditions
![]() and
and
![]() .
The
figure is plotted for the interval
-100<T<100. Evidently the
inversion symmetry implies that an another solution of this
equation for the same value of a but with the initial values
.
The
figure is plotted for the interval
-100<T<100. Evidently the
inversion symmetry implies that an another solution of this
equation for the same value of a but with the initial values
![]() and
and
![]() will be exactly
inverse-symmetric. In this particular example these initial values
are
will be exactly
inverse-symmetric. In this particular example these initial values
are
![]() and
and
![]() .
The inversion symmetry of
these solutions is apparent. Physically this fact implies that the
presence of the shear flow ensures burst-like and robust increase
of amplitudes (energy) of some Alfvén waves, while there are
always other waves which, on the contrary, sharply loose their
energy under the influence of the shear flow.
.
The inversion symmetry of
these solutions is apparent. Physically this fact implies that the
presence of the shear flow ensures burst-like and robust increase
of amplitudes (energy) of some Alfvén waves, while there are
always other waves which, on the contrary, sharply loose their
energy under the influence of the shear flow.
Momentary appearance of the transient instability on the presented
graphs is related to the narrowness of the transient instability
interval, which is apparent from Fig. 1. Note that the plotting
time interval in Fig. 1 is taken very narrow in order to give
magnified portrait of the behavior of
![]() ,
while
Figs. 2 and 3 are deliberately drawn for the much wider range in order
to illustrate the behavior of waves on a large time span.
,
while
Figs. 2 and 3 are deliberately drawn for the much wider range in order
to illustrate the behavior of waves on a large time span.
The family of solutions
![]() of (31) does not represent a
physical variable of the problem, so in order to recover
information about the temporal evolution of perturbations for
physical variables it is more convenient to solve numerically (22-23)
and to recover components of vectors
of (31) does not represent a
physical variable of the problem, so in order to recover
information about the temporal evolution of perturbations for
physical variables it is more convenient to solve numerically (22-23)
and to recover components of vectors ![]() and
and ![]() from (24). Besides, it is instructive to calculate the kinetic
energy, the magnetic energy and the total energy of perturbations
as given by (25). In order to track the temporal evolution of the
shear-modified wave branch as such we set the amplitude of the
unmodified component
from (24). Besides, it is instructive to calculate the kinetic
energy, the magnetic energy and the total energy of perturbations
as given by (25). In order to track the temporal evolution of the
shear-modified wave branch as such we set the amplitude of the
unmodified component
![]() to be zero
to be zero
![]() .
Alternatively our numerical task was, first, to solve Eq. (28) in
order to get functions
.
Alternatively our numerical task was, first, to solve Eq. (28) in
order to get functions ![]() and
and
![]() .
Second
step was to calculate the physical variables by means of
Eqs. (22)-(25).
.
Second
step was to calculate the physical variables by means of
Eqs. (22)-(25).
This set of calculations was performed for different values of the
system parameters and some representative examples are given in
Figs. 4 and 5. Note that they are plotted as functions of the real
time variable t and not the variable T used in (31). From
these figures we readily see that when
![]() (
(
![]() ), the shear flow efficiently "pumps" energy into
the longitudinal components of the velocity and the magnetic field
perturbations, while the transverse components stay basically
unchanged aside from the transitory, "burst-like" increase of
their amplitudes in the brief, transient amplification phase. This
is another indication of the above-mentioned fact that the
velocity shear primarily affects the incompressible limit of the
fast magnetosonic waves. The asymptotic increase of the total
energy, as shown in Fig. 4, being entirely due to the increase in
vz and bz, is quite substantial (about two orders of
magnitude for the given example).
), the shear flow efficiently "pumps" energy into
the longitudinal components of the velocity and the magnetic field
perturbations, while the transverse components stay basically
unchanged aside from the transitory, "burst-like" increase of
their amplitudes in the brief, transient amplification phase. This
is another indication of the above-mentioned fact that the
velocity shear primarily affects the incompressible limit of the
fast magnetosonic waves. The asymptotic increase of the total
energy, as shown in Fig. 4, being entirely due to the increase in
vz and bz, is quite substantial (about two orders of
magnitude for the given example).
![\begin{figure}
\par\includegraphics[angle=90,width=8cm,clip]{plot5.ps} \end{figure}](/articles/aa/full/2003/08/aah3329/Timg150.gif) |
Figure 5: The numerical solution of Eqs. (22)-(23) with the same parameters as in Fig. 4 except ky=10.1. |
This is a typical mode of behavior for perturbations with
![]() and it is quite similar with the behavior of
hydromagnetic waves in plane shear flows (Chagelishvili et al. 1993). By
imparting a small but nonzero
and it is quite similar with the behavior of
hydromagnetic waves in plane shear flows (Chagelishvili et al. 1993). By
imparting a small but nonzero ![]() (see Fig. 5), we can make
all perturbation components grow. However, the overall increase of
the total energy of perturbations in the latter case is somewhat
smaller than in the former case.
(see Fig. 5), we can make
all perturbation components grow. However, the overall increase of
the total energy of perturbations in the latter case is somewhat
smaller than in the former case.
Copyright ESO 2003