For more complicated MHD flows, the time evolution of the
wavenumber vector
![]() ,
governed by Eqs. (14),
becomes nonlinear and it makes the temporal behavior of
linear perturbations much more complex. A relatively simple, 2-D
hydrodynamic system of such complexity was recently investigated
(Mahajan & Rogava 1999). For the MHD helical flow, specified by the
shear matrix (11) and considered in this section, we may deduce
from (15) and (13c) that the perturbations may grow either
exponentially (when differential rotation rate n>1), or vary in
time in a periodic way (when n<1). Below we develop the
mathematical formalism for the study of perturbation evolution for
these two classes of solutions.
,
governed by Eqs. (14),
becomes nonlinear and it makes the temporal behavior of
linear perturbations much more complex. A relatively simple, 2-D
hydrodynamic system of such complexity was recently investigated
(Mahajan & Rogava 1999). For the MHD helical flow, specified by the
shear matrix (11) and considered in this section, we may deduce
from (15) and (13c) that the perturbations may grow either
exponentially (when differential rotation rate n>1), or vary in
time in a periodic way (when n<1). Below we develop the
mathematical formalism for the study of perturbation evolution for
these two classes of solutions.
The starting set of equations is again (16)-(19). Taking time
derivative of (16) we find out that
| (33) |
| (34) | |||
| (35) |
| (36) |
| (37) |
We can reduce (34) and (35) to the following explicit second-order
equation for the magnetic field:
| (38) |
Obviously (38) is a general equation and we can base our analysis
on it. However a different approach may also be useful. Let us
introduce "projection variables":
| (39a) | |||
| (39b) | |||
| (39c) | |||
| (39d) |
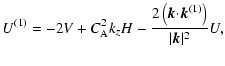 |
(40) | ||
| H(1)=-kzU, | (41) | ||
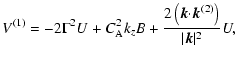 |
(42) | ||
| B(1)=-kzV. | (43) |
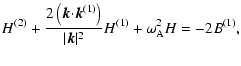 |
(44) | ||
| (45) |
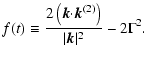 |
(46) |
| (47) |
![$\displaystyle {\Psi}^{(2)}+{\left[{\omega}_{\rm A}^2-\vert\vec R\vert^2-{{\left...
...ight)}\over {\vert{\vec k}\vert^2}}\right]}{\Psi}=-2\vert{\vec k}\vert B^{(1)}.$](/articles/aa/full/2003/08/aah3329/img175.gif) |
(48) |
Depending on the actual type of the motion in the plane normal to
Z there will be different regimes of the time variation of
![]() (see for details Mahajan & Rogava 1999). Instabilities are present
both when the wavenumber varies exponentially and periodically.
(see for details Mahajan & Rogava 1999). Instabilities are present
both when the wavenumber varies exponentially and periodically.
In the former case, i.e., when the absolute value of
![]() increases exponentially, the dissipation effects will
eventually start to be important and try to damp the
mode (Mahajan & Rogava 1999) despite the presence of the shear instability.
The same argument is valid for those cases,
too, when the temporal growth of the wavenumber is linear. Therefore,
considering shear-induced nonmodal effects in inviscid fluids in cases
when
increases exponentially, the dissipation effects will
eventually start to be important and try to damp the
mode (Mahajan & Rogava 1999) despite the presence of the shear instability.
The same argument is valid for those cases,
too, when the temporal growth of the wavenumber is linear. Therefore,
considering shear-induced nonmodal effects in inviscid fluids in cases
when
![]() is monotonously increasing, we should realize that
the description is physically meaningful only for initial (finite)
times.
is monotonously increasing, we should realize that
the description is physically meaningful only for initial (finite)
times.
![\begin{figure}
\par\includegraphics[angle=90,width=8.1cm,clip]{plot6.ps}\end{figure}](/articles/aa/full/2003/08/aah3329/Timg177.gif) |
Figure 6:
The numerical solution for the case when temporal evolution of
|
It is worthwhile to make a look at some of these solutions. In
Fig. 6 we present the results of numerical calculations, taken for
the case, when kx=5, ky=10, kz=1,
![]() ,
A1=0.3,
A2=10-2, C1=0.8, C2=0.9,
,
A1=0.3,
A2=10-2, C1=0.8, C2=0.9,
![]() .
The
value of
.
The
value of
![]() is positive and the value
of
is positive and the value
of
![]() is exponentially increasing (see Fig. 6a). The
characteristic amplification time scale
is exponentially increasing (see Fig. 6a). The
characteristic amplification time scale
![]() is of the order of the period of
rotation. The resulting wave evolves accordingly, which is clearly
visible from the figures. It is noteworthy to see that, analogous
to the pure outflow case, shear flow energy is most efficiently
absorbed by the longitudinal components of the velocity and the
magnetic field perturbations. Still, now, the energy growth,
plotted again for the
is of the order of the period of
rotation. The resulting wave evolves accordingly, which is clearly
visible from the figures. It is noteworthy to see that, analogous
to the pure outflow case, shear flow energy is most efficiently
absorbed by the longitudinal components of the velocity and the
magnetic field perturbations. Still, now, the energy growth,
plotted again for the
![]() ,
is not algebraic
but exponential and is entirely due to the exponential evolution
of the perturbation wave number vector.
,
is not algebraic
but exponential and is entirely due to the exponential evolution
of the perturbation wave number vector.
When values of
![]() are negative, the temporal evolution
of
are negative, the temporal evolution
of
![]() 's is periodic, which means that the absolute value
of the wavenumber vector stays bounded within certain limits. It
means that in this case shear-induced effects have potentially
much wider durability and may potentially lead to strongly
perceptible effects. The limits of this paper does not allow us to
present full analysis of all possible classes of solutions. The
most interesting feature of this case is that Alfvén waves
become parametrically unstable in a helical flow. Figures 7-9
demonstrate this noteworthy fact. All figures are drawn for the
case when
A1=-A2=0.3, and
's is periodic, which means that the absolute value
of the wavenumber vector stays bounded within certain limits. It
means that in this case shear-induced effects have potentially
much wider durability and may potentially lead to strongly
perceptible effects. The limits of this paper does not allow us to
present full analysis of all possible classes of solutions. The
most interesting feature of this case is that Alfvén waves
become parametrically unstable in a helical flow. Figures 7-9
demonstrate this noteworthy fact. All figures are drawn for the
case when
A1=-A2=0.3, and
![]() ,
so that
,
so that
![]() .
Figure 7 shows the case
when Alfvén frequency is
.
Figure 7 shows the case
when Alfvén frequency is
![]() .
The system is
still out of the parametric resonance and the system, therefore,
exhibits just Alfvén waves, modulated by the periodic shear.
The picture is drastically different when
.
The system is
still out of the parametric resonance and the system, therefore,
exhibits just Alfvén waves, modulated by the periodic shear.
The picture is drastically different when
![]() - Fig. 8 shows that there appears a robust instability of
parametric (resonant) nature that leads to the strong exponential
increase of the system energy in the same span of time as in
Fig. 7. The resonance is quite sharp, because as soon as Alfvén
frequency slightly exceeds the value of W the system becomes
stable again, as it is visible from the Fig. 9, which is drawn for
the case when
- Fig. 8 shows that there appears a robust instability of
parametric (resonant) nature that leads to the strong exponential
increase of the system energy in the same span of time as in
Fig. 7. The resonance is quite sharp, because as soon as Alfvén
frequency slightly exceeds the value of W the system becomes
stable again, as it is visible from the Fig. 9, which is drawn for
the case when
![]() .
.
![\begin{figure}
\par\includegraphics[angle=90,width=8.2cm,clip]{plot8.ps} \end{figure}](/articles/aa/full/2003/08/aah3329/Timg184.gif) |
Figure 8:
The numerical solution for the case when
|
![\begin{figure}
\par\includegraphics[angle=90,width=8.3cm,clip]{plot9.ps} \end{figure}](/articles/aa/full/2003/08/aah3329/Timg185.gif) |
Figure 9:
The numerical solution for the case when
|
Further study shows that actually there are several isolated
regions of instability, which happen to be centered around the
values
![]() and usually first resonance
and usually first resonance
![]() is the most efficient one. This is a strong
indication in favor of the resonant and parametric nature of this
instability. Figures 10 and 11 illustrate this
interesting property of the system. The plots are drawn for the
total energy of a perturbation, normalized on its initial value:
is the most efficient one. This is a strong
indication in favor of the resonant and parametric nature of this
instability. Figures 10 and 11 illustrate this
interesting property of the system. The plots are drawn for the
total energy of a perturbation, normalized on its initial value:
![]() .
The simulation is made for
the case when kx=20, ky=5, kz=1,
.
The simulation is made for
the case when kx=20, ky=5, kz=1,
![]() ,
A1=0.5, A2=-0.9, Cx=0.01, Cy=0.05. Note that in this
case W=0.3. Making simulations for different values of the
Alfvén velocity we see that perturbations are strongly unstable
when
,
A1=0.5, A2=-0.9, Cx=0.01, Cy=0.05. Note that in this
case W=0.3. Making simulations for different values of the
Alfvén velocity we see that perturbations are strongly unstable
when
![]() .
Namely the instability is present in
Figs. 10a, c and Figs. 11a, c, where the values of
.
Namely the instability is present in
Figs. 10a, c and Figs. 11a, c, where the values of
![]() are 0.3, 0.6, 0.9, and 1.2, respectively. At
the same time we see that for intermediate values of
are 0.3, 0.6, 0.9, and 1.2, respectively. At
the same time we see that for intermediate values of
![]() ,
when
,
when
![]() ,
the Alfvén waves stay stable.
Unfortunately the complexity of the system does not allow us to
perform strict analytic analysis and locate the actual width and
size of instability regions. However, our results do show that
there are several such regions and presumably the efficiency of
the instability decreases with the increase of n.
,
the Alfvén waves stay stable.
Unfortunately the complexity of the system does not allow us to
perform strict analytic analysis and locate the actual width and
size of instability regions. However, our results do show that
there are several such regions and presumably the efficiency of
the instability decreases with the increase of n.
![\begin{figure}
\par\includegraphics[angle=90,width=8cm,clip]{plot11.ps}\end{figure}](/articles/aa/full/2003/08/aah3329/Timg192.gif) |
Figure 11:
The numerical solution for the total energy of
perturbations. The values of parameters are the same as in
Fig. 10. while
|
Copyright ESO 2003