

Up: Swirling astrophysical flows -
Our aim is to develop a theory of collective phenomena in helical
flows of magnetized plasmas. We adopt the standard MHD model and
consider incompressible perturbations in an axisymmetric,
cylindrical, steady flow of a plasma with uniform density
(
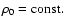 ), embedded in a vertical, homogeneous
), embedded in a vertical, homogeneous
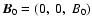 magnetic field. With
magnetic field. With
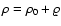 ,
P=P0+p,
,
P=P0+p,
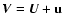 ,
,
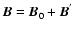 ,
the basic set of MHD equations for linearized
perturbations is:
,
the basic set of MHD equations for linearized
perturbations is:
where
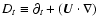 is the convective derivative operator and
is the convective derivative operator and
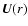 is the vector field of the steady state flow. Unfortunately
the actual kinematic portrait of astrophysical helical flows is
largely unknown. There is no credible data for recently
discovered solar macrospicules with helical plasma motion (solar tornados), for accretion columns related to X-ray
pulsars and cataclysmic variables, for accretion-ejection flows and galactic and
extragalactic jets. Therefore, we need to adopt a
phenomenological model for
is the vector field of the steady state flow. Unfortunately
the actual kinematic portrait of astrophysical helical flows is
largely unknown. There is no credible data for recently
discovered solar macrospicules with helical plasma motion (solar tornados), for accretion columns related to X-ray
pulsars and cataclysmic variables, for accretion-ejection flows and galactic and
extragalactic jets. Therefore, we need to adopt a
phenomenological model for 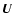 ,
that has to be general
enough to encompass different possible sorts of real helical
flows. Preferably the model must be three-dimensional and it
should include a possibility of both outflowing/inflowing and
rotational modes of motion. The model we choose is (Rogava & Poedts 1999):
,
that has to be general
enough to encompass different possible sorts of real helical
flows. Preferably the model must be three-dimensional and it
should include a possibility of both outflowing/inflowing and
rotational modes of motion. The model we choose is (Rogava & Poedts 1999):
![$\displaystyle {\vec U}(r)\equiv[0,~r{\Omega}(r),~U(r)],$](/articles/aa/full/2003/08/aah3329/img42.gif) |
|
|
(5) |
where
r=(x2+y2)1/2 is a distance from the rotation axis.
For the angular velocity we take:
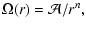 |
|
|
(6) |
with 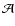 and n as constants. This model implies the
following two limiting cases:
and n as constants. This model implies the
following two limiting cases:
-
Rigid rotation, with n=0 and
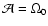 .
.
-
Keplerian rotation, with n=3/2 and
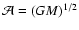 .
.
The corresponding Cartesian components of the linear azimuthal
velocity
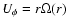 are:
are:
| |
|
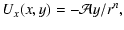 |
(7a) |
| |
|
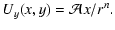 |
(7b) |
The basic role in our analysis is played by the shear matrix
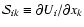 .
Evidently rotational part of the flow velocity generates the following four nonzero
components of the shear
matrix:
.
Evidently rotational part of the flow velocity generates the following four nonzero
components of the shear
matrix:
As regards the outflow component of the velocity we can use the model (Rogava et al. 2000):
![\begin{displaymath}U_z(x,y)=U_m\left[1-(r/R)^2\right],
\end{displaymath}](/articles/aa/full/2003/08/aah3329/img56.gif) |
(9a) |
comprising a parabolically
sheared "outflow" along the Z-axis, being similar to the well-known Hagen-Poiseuille flow.
The outflow model may be modeled also in a number of other ways. In astrophysical jet
literature, for instance, the model (Ferrari 1998):
![\begin{displaymath}U_z=U_m/{\rm cosh}[r^m],
\end{displaymath}](/articles/aa/full/2003/08/aah3329/img57.gif) |
(9b) |
is often used. One can easily see
that the outflow component, given by (9), generates the following
two components of the shear matrix:
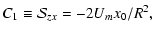 |
|
|
(10a) |
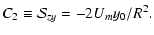 |
|
|
(10b) |
Therefore, the resulting helical flow is the superposition of a
cylindrical outflow along the Z-axis
with a differential motion in the
transverse cross-section of the jet. The complete
 traceless shear matrix is:
traceless shear matrix is:
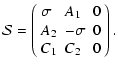 |
|
|
(11) |
This shear matrix has a number of interesting properties. Its square is
equal to:
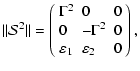 |
|
|
(12) |
where we use the notation:
and its cube is:
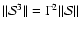 .
.
The nonmodal local method for studying the dynamics of linearized
perturbations in kinematically complex flows (Lagnado et al. 1984; Craik & Criminale 1986;
Mahajan & Rogava 1999) allows to reduce the initial set of partial differential equations
for perturbation variables
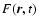 ,
defined in the real physical space,
to the initial value
problem formulated for the perturbation variable amplitudes
,
defined in the real physical space,
to the initial value
problem formulated for the perturbation variable amplitudes
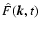 ,
defined in the space
of wave numbers (k-space). The key element of this approach is the
time variability of
,
defined in the space
of wave numbers (k-space). The key element of this approach is the
time variability of 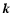 's, imposed by the presence of the shear flow!
This variability is governed by the following set of equations:
's, imposed by the presence of the shear flow!
This variability is governed by the following set of equations:
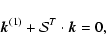 |
(14) |
henceforth for an arbitrary function f we use the notation:
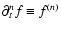 .
.
For the helical flow we find that
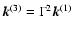 .
The corresponding characteristic equation
.
The corresponding characteristic equation
![${\rm det}[{\cal S}^T-{\lambda}{\times}
{\cal I}]=0$](/articles/aa/full/2003/08/aah3329/img73.gif) (with
(with 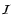 being a unit matrix) yields the equation for the
eigenvalues:
being a unit matrix) yields the equation for the
eigenvalues:
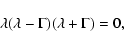 |
(15a) |
with the solutions:
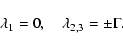 |
(15b) |
We see that the differential rotation parameter nplays a decisive role in determining the evolution scenario for the
wave number vector
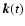 :
when n<1 (including the
rigid rotation case)
:
when n<1 (including the
rigid rotation case) 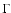 is imaginary and the time evolution
of
is imaginary and the time evolution
of
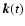 is periodic, while when n>1 (including the
Keplerian rotation regime),
is periodic, while when n>1 (including the
Keplerian rotation regime), 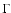 is real and makes the time
behavior of
is real and makes the time
behavior of
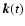 exponential.
exponential.
In the dimensionless notation
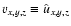 ,
,
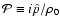 ,
,
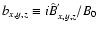 ,
perturbation amplitudes
evolve as:
,
perturbation amplitudes
evolve as:
In the next two sections we separately consider the problem of a purely
ejectional/injectional flow, and a flow with helical motion
of plasma particles. We shall see that in both cases the Alfvén waves sustained by the flow
are amplified. For the former case the amplification is transient (algebraic instability),
while for the latter case the velocity shear makes Alfvén waves exponentially unstable.


Up: Swirling astrophysical flows -
Copyright ESO 2003
![]() ), embedded in a vertical, homogeneous
), embedded in a vertical, homogeneous
![]() magnetic field. With
magnetic field. With
![]() ,
P=P0+p,
,
P=P0+p,
![]() ,
,
![]() ,
the basic set of MHD equations for linearized
perturbations is:
,
the basic set of MHD equations for linearized
perturbations is:
![\begin{displaymath}U_z(x,y)=U_m\left[1-(r/R)^2\right],
\end{displaymath}](/articles/aa/full/2003/08/aah3329/img56.gif)
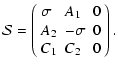
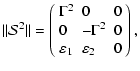
![]() ,
defined in the real physical space,
to the initial value
problem formulated for the perturbation variable amplitudes
,
defined in the real physical space,
to the initial value
problem formulated for the perturbation variable amplitudes
![]() ,
defined in the space
of wave numbers (k-space). The key element of this approach is the
time variability of
,
defined in the space
of wave numbers (k-space). The key element of this approach is the
time variability of ![]() 's, imposed by the presence of the shear flow!
This variability is governed by the following set of equations:
's, imposed by the presence of the shear flow!
This variability is governed by the following set of equations:
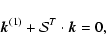
![]() .
The corresponding characteristic equation
.
The corresponding characteristic equation
![]() (with
(with ![]() being a unit matrix) yields the equation for the
eigenvalues:
being a unit matrix) yields the equation for the
eigenvalues:
![]() ,
,
![]() ,
,
![]() ,
perturbation amplitudes
evolve as:
,
perturbation amplitudes
evolve as: