

Up: On the detectability of
Subsections
In this section first we show how the presence of the dynamical term can influence the usual
method of light-time solutions, and then, we give a numerical method to separate
the two terms, which can improve the accuracy of the light-time solution, and, furthermore,
may give additional information about the spatial orientation of the triple system.
A usual way of calculation of the light-time solution is based on the fact that there are
some very simple relations (at least in the first and second order in e') between the orbital
elements of the wide orbit and the first two or three pairs of coefficients of the Fourier-expansion
of the light-time curve, where the fundamental frequency is the period ratio, e.g. 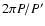 .
Consequently, if the harmonic coefficients of the O-C were determined by some numerical methods (typically by
weighted least-squares fit), then the orbital elements could be calculated in a very simple way.
.
Consequently, if the harmonic coefficients of the O-C were determined by some numerical methods (typically by
weighted least-squares fit), then the orbital elements could be calculated in a very simple way.
For the sake of completeness we describe here the most important formulae after Kopal (1978, Chap. V).
In the case of the pure light-time effect the mathematical form of the O-C curve is:
![\begin{displaymath}%
{\rm O}{-}{\rm C}=\sum_{k=1}^\infty\left[a_k\sin(k\nu N)+b_k\cos(k\nu N)\right]-\sum_{k=1}^\infty b_k,
\end{displaymath}](/articles/aa/full/2003/06/aah4008/img120.gif) |
(49) |
where N is the cycle number, and
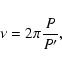 |
(50) |
while
| |
|
![$\displaystyle a_k=A\left[g_k\left(e'\right)\cos\omega'\cos{kl'_0}-h_k\left(e'\right)\sin\omega'\sin{kl'_0}\right],$](/articles/aa/full/2003/06/aah4008/img122.gif) |
(51) |
| |
|
![$\displaystyle b_k=A\left[g_k\left(e'\right)\cos\omega'\sin{kl'_0}+h_k\left(e'\right)\sin\omega'\cos{kl'_0}\right],$](/articles/aa/full/2003/06/aah4008/img123.gif) |
(52) |
where
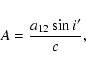 |
(53) |
furthermore,
| |
|
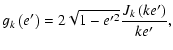 |
(54) |
| |
|
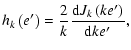 |
(55) |
and in the latter expressions Jk represents the Besselian function of the kth order. (We note, that in (53)
c stands for the velocity of light.) Considering
a quadratic approximation in the outer eccentricity the non-zero coefficients are as follows:
| |
|
![$\displaystyle a_1=A\left[\left(1-\frac{3e'^2}{8}\right)\cos\left(l'_0+\omega'\right)-\frac{e'^2}{4}\cos\omega'\cos{l'_0}\right],$](/articles/aa/full/2003/06/aah4008/img127.gif) |
(56) |
| |
|
![$\displaystyle b_1=A\left[\left(1-\frac{3e'^2}{8}\right)\sin\left(l'_0+\omega'\right)-\frac{e'^2}{4}\cos\omega'\sin{l'_0}\right],$](/articles/aa/full/2003/06/aah4008/img128.gif) |
(57) |
| |
|
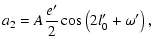 |
(58) |
| |
|
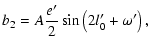 |
(59) |
| |
|
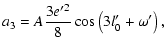 |
(60) |
| |
|
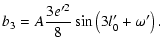 |
(61) |
Using the expansions of Cayley (1861) Eq. (46) also can be easily expanded into trigonometric series of the
mean anomaly l', as
where
We omitted terms which are multiplied by
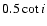 ,
as in eclipsing systems the observable inclination of the
binary is usually close to
,
as in eclipsing systems the observable inclination of the
binary is usually close to
 ,
consequently these terms give only a minor contribution. (E.g. even for
,
consequently these terms give only a minor contribution. (E.g. even for
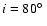 ,
,
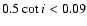 .)
A comparison between (62) and (49) reveals that in this case the coefficients are
as follows:
.)
A comparison between (62) and (49) reveals that in this case the coefficients are
as follows:
| |
|
![$\displaystyle a^*_1=A^*e'\left[{\cal{M}}\cos{l'_0}-{\cal{S}}\cos\left(l'_0+2\omega'\right)+{\cal{C}}\sin\left(l'_0+2\omega'\right)\right],$](/articles/aa/full/2003/06/aah4008/img143.gif) |
(66) |
| |
|
![$\displaystyle b^*_1=A^*e'\left[{\cal{M}}\sin{l'_0}-{\cal{S}}\sin\left(l'_0+2\omega'\right)-{\cal{C}}\cos\left(l'_0+2\omega'\right)\right],$](/articles/aa/full/2003/06/aah4008/img144.gif) |
(67) |
| |
|
![$\displaystyle a_2^*=A^*\left[{\cal{S}}\cos2\left(l'_0+\omega'\right)-{\cal{C}}\sin2\left(l'_0+\omega'\right)\right],$](/articles/aa/full/2003/06/aah4008/img145.gif) |
(68) |
| |
|
![$\displaystyle b_2^*=A^*\left[{\cal{S}}\sin2\left(l'_0+\omega'\right)+{\cal{C}}\cos2\left(l'_0+\omega'\right)\right],$](/articles/aa/full/2003/06/aah4008/img146.gif) |
(69) |
| |
|
![$\displaystyle a_3^*=A^*\frac{7e'}{3}\left[{\cal{S}}\cos\left(3l'_0+2\omega'\right)-{\cal{C}}\sin\left(3l'_0+2\omega'\right)\right],$](/articles/aa/full/2003/06/aah4008/img147.gif) |
(70) |
| |
|
![$\displaystyle b_3^*=A^*\frac{7e'}{3}\left[{\cal{S}}\sin\left(3l'_0+2\omega'\right)+{\cal{C}}\cos\left(3l'_0+2\omega'\right)\right],$](/articles/aa/full/2003/06/aah4008/img148.gif) |
(71) |
where the amplitude A* is
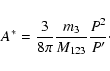 |
(72) |
(It will be seen in the next section, that in the case of systems interesting for us, for moderate
outer eccentricities, the order of A* is about Ae'. This is the reason why the quadratic
terms were held in (56)-(61).)
It is evident that a numerical modelling of the O-C curve in the form (49) yields to
coefficients which are the sums of the corresponding (56)-(61) and (66)-(71) terms.
Now some qualitative remarks can be easily done about the effect of the dynamical terms on a usual
light-time solution. First, if the third star revolves in a circular orbit, which is coplanar with the
orbit of the binary, the dynamical terms diminish, e.g. the geometrical terms are unaffected in that case.
Furthermore, for a non-coplanar, but circular outer orbit, the amplitude of the light-time solution remains
invariant, at least as far as the quadratic term is not counted. On the other hand, in the case of this configuration
the usual determination of the outer eccentricity (from the second Fourier-coefficients) may give
an error of several 10 percents. Finally, if the outer orbit is significantly eccentric, both the mass-function
(via the amplitude), and the outer eccentricity is affected.
The separation of the dynamical terms from the light-time curve may give two important advantages. The first
is the determination of more accurate orbital elements, mainly the "projected'' third-body mass. The second one is the possibility to determine the relative spatial orientation of the two orbital planes.
This latter arises from the fact, that the dynamical terms - through the orbital elements which determine
the light-time orbit - depend on the third body mass (m3), the observable inclination of the wide orbit
(i'), and the mutual inclination (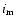 ). It is evident that the dependence on m3 appears in the
amplitude A*, while the effect of the inclinations manifests through the following equations of spherical triangles:
). It is evident that the dependence on m3 appears in the
amplitude A*, while the effect of the inclinations manifests through the following equations of spherical triangles:
In order to make this separation we developed a computer code which is based on a non-linear
Levenberg-Marquardt algorithm (see Press et al. 1989, Chap. 14.4). In the present state the code adjusts the following eight parameters: c0 (a zero-point correction), P, A (the amplitude
of the light-time terms), e', 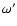 ,
l'0, i', and instead of the mutual inclination,
,
l'0, i', and instead of the mutual inclination,
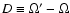 .
(Here we note, that although P is an adjusted parameter, de fundamental frequency
.
(Here we note, that although P is an adjusted parameter, de fundamental frequency 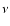 is constant during
the iteration.) The partial derivatives of the coefficients (56)-(71) are listed in the Appendix.
is constant during
the iteration.) The partial derivatives of the coefficients (56)-(71) are listed in the Appendix.
The method of the computation is the following. As a first step we determine the light-time solution from the O-C curve in the usual way. These orbital elements are used as input parameters for the Levenberg-Marquardt
method. For the remaining two parameters (i', D) several initial trial-values are applied automatically.
(Using the mass-function, the mass m3 and the amplitude A* are calculated in each iteration step.)
If a solution is convergent, the program saves the final parameters, and takes
the following set of the angular (i', D) parameters.
The results of our numerical fitting can be found in Tables 4, 5.
In the case of the "Algol-like'' system we deduced the following conclusions:
- In most cases more accurate orbital elements were gained for the elements e',
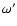 ,
,
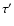 than
it was obtained from the simple light-time (L) fit. In these runs the
than
it was obtained from the simple light-time (L) fit. In these runs the 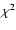 value also improved with respect to the corresponding L-fits;
value also improved with respect to the corresponding L-fits;
- Significant exceptions arise in fits A3, A6, A12, e.g. at those runs, where
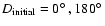 .
In these cases
.
In these cases
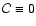 ,
while
,
while
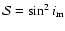 ,
which is also zero for run A3, while
,
which is also zero for run A3, while
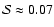 and
and
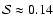 for runs A6 and A12, respectively.
Consequently, in these
cases only the
for runs A6 and A12, respectively.
Consequently, in these
cases only the 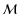 -term, and the coefficients a*1, b*1 have significant contributions.
On the other hand, in run A15, where
-term, and the coefficients a*1, b*1 have significant contributions.
On the other hand, in run A15, where
 was zero a good fit was also found. In this case
already the
was zero a good fit was also found. In this case
already the
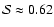 term is the dominant. (Here we note, that in this integration
the mutual inclination was
term is the dominant. (Here we note, that in this integration
the mutual inclination was
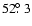 ,
which is very close to that "critical'' value where the
,
which is very close to that "critical'' value where the
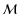 -term disappears.) It is interesting, that despite the weaker fits in these cases, the
-term disappears.) It is interesting, that despite the weaker fits in these cases, the
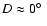 ,
,
 values were reproduced well;
values were reproduced well;
- The determination of the visible inclination of the outer orbit is less accurate. This is of course not
so surprising. We note that the dependence of the tertiary mass on the visible inclination (i') is very
weak in the high inclination region. A comparison of the upper or the middle panels in Fig. 2
shows this clearly. Nevertheless, for the last three runs (in the low visible inclination region), where a smaller variation in
the visible inclination i' results already significant
variation in m3, really a smaller inclination, and consequently larger third body mass was found;
- Finally, we can conclude that the better fits were reached when the mutual inclination had
a medium value.
Considering the "I'' runs with the parameters of the IU Aur system our results
are less satisfactory (see Table 5).
Although the light-time parameters were improved in more than the half of these runs, the accuracy is far from
that achieved in the "A'' runs. What could be the reason? There are three significant differences between the
configurations of the two systems. The first is the large outer eccentricity in the IU Aur system, while
the other two are the larger masses of the stars, and the smaller P'/P ratio, e.g. the closeness of this triple.
The effects of these properties for the behaviour of our solution are very complex. A purely mathematical
effect is that due to the larger eccentricity our expression gives a weaker approximation. On the other hand, we note,
as perhaps the most important physical effect, that because the latter system is more compact, the apse-node time scale
of the largest amplitude perturbations is significantly shorter, and these disturbances may manifest on the O-C
diagram within years. (E.g. according to Drechsel et al. 1994 the period of the nodal regression is about 300 years
in the IU Aur system.)
In order to study these two above mentioned phenomena we carried out the following two tests. In the last run (I10)
we changed the outer eccentricity for the value e'=0.24, while the other parameters had the same values as in
run I5. A significant improvement was found in most of the parameters (although a false result also occurred).
Furthermore, we calculated the O-C solution of run I1 for a shorter (about half of the original) time interval.
(These results are listed in the "I1S'' rows of Table 5.) We did not find significant discrepancy
with respect to the original "I1'' solutions. We can conclude, that the larger eccentricity plays a more important role in our weaker results in this case.


Up: On the detectability of
Copyright ESO 2003
![]() .
Consequently, if the harmonic coefficients of the O-C were determined by some numerical methods (typically by
weighted least-squares fit), then the orbital elements could be calculated in a very simple way.
.
Consequently, if the harmonic coefficients of the O-C were determined by some numerical methods (typically by
weighted least-squares fit), then the orbital elements could be calculated in a very simple way.
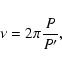
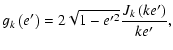
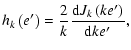
![]() ). It is evident that the dependence on m3 appears in the
amplitude A*, while the effect of the inclinations manifests through the following equations of spherical triangles:
). It is evident that the dependence on m3 appears in the
amplitude A*, while the effect of the inclinations manifests through the following equations of spherical triangles: