

Up: On the detectability of
Subsections
By the use of the theory of Harrington (1968, 1969), based on the von Zeipel averaging method of the canonical equations,
Söderhjelm (1975, 1982) derived analytical formulae for the long period perturbations in the standard Delaunay variables.
Although these formulae are exact up to second order in the (a/a') ratio, their practical use is limited, at least in their original
forms. Mayer (1990) gave a simple, useful form with the assumptions that the elements of the wide orbit are constant, the close
orbit is circular, and the relative orientation of the two planes is invariant. Nevertheless, as it will be shown,
the expression of Mayer (1990) maybe somewhat inaccurate. More explanation will come later.
In the following we present a corrected new formula, which is valid for the same assumptions.
Such a solution could be get easily from the original formulae of Söderhjelm as it was done by Mayer. Despite
this fact we follow a different way. Instead of the perturbing potential we depart from the perturbing force, and we calculate directly
the perturbations in the eclipsing period in the function of the true anomaly of the eclipsing pair along the wide orbit. As it will be shown
this method is more effective and faster for this particular problem, than the usual methods, furthermore, this automatically helps
to avoid that kind of inaccuracies which occured in the former solution.
![\begin{figure}
\par\includegraphics[width=12cm,clip]{h4008f1.eps}\end{figure}](/articles/aa/full/2003/06/aah4008/Timg7.gif) |
Figure 1:
The spatial orientation of the orbital planes. See text for details. |
Using the mass-point approximation, the perturbing force acting upon the close binary is:
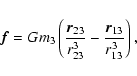 |
(1) |
where G denotes the gravitational constant, m3 is the mass of the tertiary, while
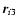 stands for
the position vector between the ith component of the binary and the third star.
The above expression, as it is well-known, can be expanded into a series of Lagrangian polynomials of the following form:
stands for
the position vector between the ith component of the binary and the third star.
The above expression, as it is well-known, can be expanded into a series of Lagrangian polynomials of the following form:
![$\displaystyle %
\vec{f}=\frac{Gm_3}{\rho_2^3}\left\{\left[\sum_{n=0}^\infty\lef...
...n\left(\frac{\rho_1}{\rho_2}\right)^nP_n(\lambda)\right]^3\vec{r}_{13}\right\},$](/articles/aa/full/2003/06/aah4008/img10.gif) |
|
|
(2) |
where M12 means the total mass of the binary,  and
and  denote the absolute value of the first two Jacobian position-vectors,
(e.g.
denote the absolute value of the first two Jacobian position-vectors,
(e.g. 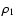 means the separation of the members of the eclipsing pair, while
means the separation of the members of the eclipsing pair, while 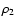 is the distance between the centre of mass of the binary and
the distant third companion), while
is the distance between the centre of mass of the binary and
the distant third companion), while 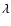 stands for the direction cosine between
stands for the direction cosine between
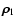 and
and
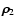 .
Let us define
a Cartesian coordinate system whose origin is at the centre of mass of the binary, and the three axes are parallel
with the vectors
.
Let us define
a Cartesian coordinate system whose origin is at the centre of mass of the binary, and the three axes are parallel
with the vectors
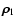 ,
,
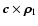 ,
,
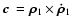 ,
respectively. The direction
cosines between the vector
,
respectively. The direction
cosines between the vector
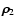 and the axes (as it can be seen in Fig. 1) are as follows:
and the axes (as it can be seen in Fig. 1) are as follows:
where w and w' denote the true longitude of the secondary and the tertiary measured from the intersection of the orbits,
and 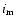 is the mutual inclination.
According to these the three (radial, transversal and normal) components of the perturbing force in the first order of the
ratio
is the mutual inclination.
According to these the three (radial, transversal and normal) components of the perturbing force in the first order of the
ratio
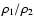 are
are
where
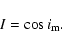 |
(10) |
(As it can be seen, the radial force component is divided into two parts. The first one contains terms depending on w, and very similar to
the 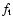 transversal component, while
transversal component, while
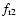 does not depend on the revolution of the eclipsing binary.)
does not depend on the revolution of the eclipsing binary.)
In what follows we will refer the orbital elements to a plane perpendicular to the line of sight of the observer,
and going accross the centre of mass of the binary. We will call it as the plane of the sky. It is clear that the
distance of this plane from the observer varies in time, according to the
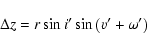 |
(11) |
function, where
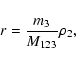 |
(12) |
furthermore v' denotes the true anomaly of the outer body, 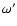 is the argument of the periastron of the binary's
orbit around the centre of mass of the triple system, and M123 stands for the total mass of the triple.
As it is well-known this motion is the source of the light-time effect detected in several triple systems.
is the argument of the periastron of the binary's
orbit around the centre of mass of the triple system, and M123 stands for the total mass of the triple.
As it is well-known this motion is the source of the light-time effect detected in several triple systems.
Using the above mentioned true anomaly, v', of the outer body, and the true longitude, u, of
the secondary measured from the plane of the sky, the force-components have the following forms:
where the phase angles are
(In the above expressions 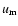 refers to the true longitude of the intersection of the two orbits
measured along the inner orbit, while
refers to the true longitude of the intersection of the two orbits
measured along the inner orbit, while
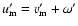 has the same meaning for the outer one.)
has the same meaning for the outer one.)
Using the expansions (13)-(16) the analytical form of the O-C can
be calculated very easily. To do that we depart from the well-known fact, that at the moment of a mid-minimum
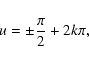 |
(19) |
where k is an integer. (Strictly speaking the above equation is valid exactly only if the eccentricity
of the eclipsing binary is zero, or the visible inclination is 90
 ,
nevertheless, in our treatment
the first condition is practically fulfilled.)
Let us define the so called instantaneous period of the binary in the following way:
,
nevertheless, in our treatment
the first condition is practically fulfilled.)
Let us define the so called instantaneous period of the binary in the following way:
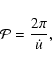 |
(20) |
where as it is well-known (see e.g. Milani et al. 1987, Chap. 3.2):
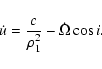 |
(21) |
Here we note an important fact. The first term on the rhs. is independent from the plane of reference, while
the second one has different values using different reference planes. (Please keep in your mind that in the
above expression, as well as in the following ones 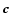 means the special angular momentum of the binary, e.g. the length of vector
means the special angular momentum of the binary, e.g. the length of vector 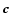 ,
and not the velocity of light.)
,
and not the velocity of light.)
Furthermore, let us denote by
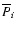 the elapsed time between the ith and the (i+1)th eclipsing
(let's say primary) minima. (Hereafter we refer to
the elapsed time between the ith and the (i+1)th eclipsing
(let's say primary) minima. (Hereafter we refer to
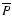 as eclipsing period.) Then it can be seen easily that
as eclipsing period.) Then it can be seen easily that
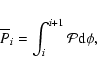 |
(22) |
where
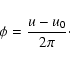 |
(23) |
According to this the eclipsing period is the average of the instantaneous period during a revolution.
Consequently the occurrence of the Nth primary minimum after a t0 epoch can be determined as
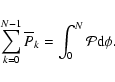 |
(24) |
Consequently, if the 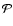 (or
(or 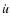 )
versus
)
versus 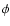 (or u) dependence is known, the theoretical form of the
O-C curve can be calculated formally by an integration. (Of course, the O-C curve is not a continuous
function, only at the integer values of the independent variable has physical meaning.)
(or u) dependence is known, the theoretical form of the
O-C curve can be calculated formally by an integration. (Of course, the O-C curve is not a continuous
function, only at the integer values of the independent variable has physical meaning.)
To get this relation we rewrite 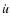 as
as
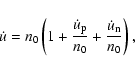 |
(25) |
where n0 stands for the mean motion of the unperturbed two-body revolution in a fixed (let's say t =t0) moment, and
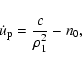 |
(26) |
while
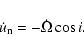 |
(27) |
As far as the perturbations are small
in the mean motion the relation between the instantaneous period 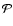 and the Keplerian period P0 of the unperturbed
motion can be written as
and the Keplerian period P0 of the unperturbed
motion can be written as
![\begin{displaymath}%
{\cal{P}}=P_0\left[1-\frac{P_0}{2\pi}(\dot{u}_{\rm p}+\dot{u}_{\rm n})\right]\cdot
\end{displaymath}](/articles/aa/full/2003/06/aah4008/img64.gif) |
(28) |
(In what follows we omit the "0'' subscripts from the initial values of the quantities referring to the unperturbed motion.)
First we calculate the effect of the
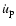 component on the instantaneous period. It can be easily seen, that
component on the instantaneous period. It can be easily seen, that
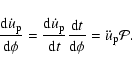 |
(29) |
The second derivative of the 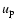 part of the true longitude has the following form (cf. Milani et al. 1987, Chap. 3.2):
part of the true longitude has the following form (cf. Milani et al. 1987, Chap. 3.2):
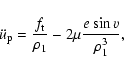 |
(30) |
where
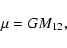 |
(31) |
and v denotes the true anomaly of the secondary component. Here we have to note an important fact. For the first sight
the presence of the second term in Eq. (30) contradicts our previous assumption, that the orbit of the binary is circular.
In fact it is not true.
Although the eccentricity is close to zero, it cannot be permanently exactly zero in perturbed systems. Even if at some moment the
close orbit was circular in the next moment due to the perturbing forces it would not be that. (For the possible
astrophysical importance of this small non-zero eccentricity especially for semi-detached systems see Eggleton et al. 1998.)
So in nearly circular systems the eccentricity oscillates between zero and a small value (typically some ten-hundredthousandths,
see e.g. our numerical integrations for the system IM Aur in Borkovits et al. 2002). In that case e approximately has
the same magnitude as 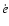 ,
and so it can be shown that the two terms on the rhs of (30) may have the
same order. Furthermore, since both
,
and so it can be shown that the two terms on the rhs of (30) may have the
same order. Furthermore, since both 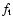 and
and 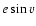 have the same order of magnitude as the small variation
in the
have the same order of magnitude as the small variation
in the 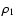 radius, the denominators in (30) can be replaced by a constant average
distance, which is the Keplerian semi-major axis a. On the other hand, we note that this is important only in the case
of the
radius, the denominators in (30) can be replaced by a constant average
distance, which is the Keplerian semi-major axis a. On the other hand, we note that this is important only in the case
of the 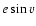 term of Eq. (30), as in the first expression the multiplicator
term of Eq. (30), as in the first expression the multiplicator 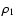 in the amplitude of
in the amplitude of
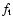 cancels the denominator.
cancels the denominator.
Let us define the expessions
| |
|
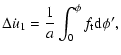 |
(32) |
| |
|
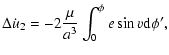 |
(33) |
respectively. Then
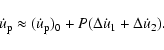 |
(34) |
For the evaluation of the first term we have to express the true anomaly of the third component by 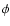 .
This can be done in two steps. First, we can change from the true anomaly to the mean anomaly by the use of the
expansions of Cayley (1861), and after that we approximate the mean anomaly l' by the following formula:
.
This can be done in two steps. First, we can change from the true anomaly to the mean anomaly by the use of the
expansions of Cayley (1861), and after that we approximate the mean anomaly l' by the following formula:
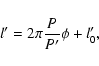 |
(35) |
where l'0 is the mean anomaly at the epoch t0. Now using the expressions
| |
|
![$\displaystyle \int_0^N\cos\left(jl'\pm{ku}\right){\rm d}\phi= \pm\frac{1}{2\pi}...
...\sin\left(jl'\pm{ku}\right)\left(1\mp\frac{j}{k}\frac{P}{P'}\right)\right]_0^N,$](/articles/aa/full/2003/06/aah4008/img76.gif) |
(36) |
| |
|
![$\displaystyle \int_0^N\sin\left(jl'\pm{ku}\right){\rm d}\phi=\mp\frac{1}{2\pi}\...
...[\cos\left(jl'\pm{ku}\right)\left(1\mp\frac{j}{k}\frac{P}{P'}\right)\right]_0^N$](/articles/aa/full/2003/06/aah4008/img77.gif) |
(37) |
the evaluation of (32) is trivial, and we get that
![\begin{displaymath}%
\Delta\dot{u}_1(\phi)=\frac{1}{4\pi}\left[\frac{f_{{\rm r1}}}{a}\right]^\phi_0\left[1+{\cal{O}}\left(P/P'\right)\right].
\end{displaymath}](/articles/aa/full/2003/06/aah4008/img78.gif) |
(38) |
Our next task is the calculation of (33). The dependence of the integrand on 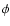 can be written as
can be written as
where the further integrands can be evaluated with good approximation as
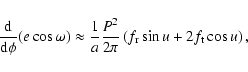 |
(40) |
and
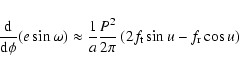 |
(41) |
(see e.g. Milani et al. 1987, Chap. 3.2).
Performing the integrations we obtain that
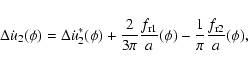 |
(42) |
where
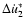 contains the constant terms and those depending upon only u (via some
trigonometric functions). These terms will not give any contribution to the values of the O-C, since they have
the same values in every minima, which fact is the direct consequence of (19).
contains the constant terms and those depending upon only u (via some
trigonometric functions). These terms will not give any contribution to the values of the O-C, since they have
the same values in every minima, which fact is the direct consequence of (19).
Finally we give the
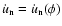 function.
As it is well known
function.
As it is well known
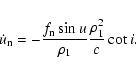 |
(43) |
Since
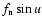 has itself the same order as the components of
has itself the same order as the components of
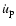 ,
the other quantities in (43) can be treated as constants.
Consequently, our approximation for
,
the other quantities in (43) can be treated as constants.
Consequently, our approximation for
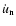 is the following:
is the following:
Let us turn back to the expression (28) of  .
It can be seen easily that all
of the above calculated perturbative terms
have the order of (P/P')2, which is in the order of 10-2-10-4 even for the closest hierarchical
systems. So, our expansion is verified.
A further integration of (28) gives the analytical form of the effect of the long period perturbations on the
O-C curve. We keep only the terms which depend also on v'. (The constant terms will give a linear contribution
to the O-C, and so they will build up into the observed eclipsing period, while terms which contain pure trigonometric
functions of u will disappear.) First let's treat the terms which depend on only the true anomaly v' of the tertiary.
For these the integration can be carried out directly with respect to v', using the expression (cf. e.g. Roy 1988, p. 292)
.
It can be seen easily that all
of the above calculated perturbative terms
have the order of (P/P')2, which is in the order of 10-2-10-4 even for the closest hierarchical
systems. So, our expansion is verified.
A further integration of (28) gives the analytical form of the effect of the long period perturbations on the
O-C curve. We keep only the terms which depend also on v'. (The constant terms will give a linear contribution
to the O-C, and so they will build up into the observed eclipsing period, while terms which contain pure trigonometric
functions of u will disappear.) First let's treat the terms which depend on only the true anomaly v' of the tertiary.
For these the integration can be carried out directly with respect to v', using the expression (cf. e.g. Roy 1988, p. 292)
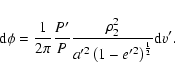 |
(45) |
Consequently, the amplitude of these integrated expressions is multiplied by
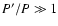 .
On the other hand, according to (36) and (37) terms which contain both v' and uafter the integration will have the same order of magnitude than before. Consequently, the terms which depend on purely
the orbital motion of the tertiary will be dominant. Keeping only these terms we obtain that
.
On the other hand, according to (36) and (37) terms which contain both v' and uafter the integration will have the same order of magnitude than before. Consequently, the terms which depend on purely
the orbital motion of the tertiary will be dominant. Keeping only these terms we obtain that
(Kepler's third law has been used for the transformation of the amplitude.)
For a comparison of our result with the formula of Mayer (1990) we enclose here his solution:
where
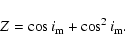 |
(48) |
(We used our notations instead of the original ones, furthermore, some obvious misprints were corrected here.)
The fundamental difference between (47) and (46) manifests in
the phase of the trigonometric terms. The phasing would be identical if 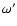 in Mayer's paper would
be measured from the intersection of the two orbital planes. Nevertheless, he used the same notation for
the argument of the periastron in the light-time contribution, where
in Mayer's paper would
be measured from the intersection of the two orbital planes. Nevertheless, he used the same notation for
the argument of the periastron in the light-time contribution, where 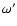 evidently has to be measured from
the plane of the sky. However, the two meanings of the
evidently has to be measured from
the plane of the sky. However, the two meanings of the 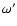 would be identical only if the observational
and the dynamical system of references were the same, or if the two orbital planes intersected each other
in the plane of the sky. As it is well-known the calculation of the perturbational
problems is usually carried out in the dynamical frame of reference, where the fundamental plane is the invariable
plane of the system. In the case of the hierarchical triple stellar systems the net angular momentum of the system
mainly concentrates in the wide orbit (see e.g. Eq. (26) of Söderhjelm 1975), consequently the plane of
the wide orbit is very close to the invariable plane, and in the immovable wide orbit approximation
(which was used by Mayer 1990) the two planes become identical.
The other discrepancies also arise from the same problem. If the plane of reference is the plane of the wide
orbit,
would be identical only if the observational
and the dynamical system of references were the same, or if the two orbital planes intersected each other
in the plane of the sky. As it is well-known the calculation of the perturbational
problems is usually carried out in the dynamical frame of reference, where the fundamental plane is the invariable
plane of the system. In the case of the hierarchical triple stellar systems the net angular momentum of the system
mainly concentrates in the wide orbit (see e.g. Eq. (26) of Söderhjelm 1975), consequently the plane of
the wide orbit is very close to the invariable plane, and in the immovable wide orbit approximation
(which was used by Mayer 1990) the two planes become identical.
The other discrepancies also arise from the same problem. If the plane of reference is the plane of the wide
orbit,
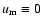 ,
consequently the terms multiplied by
,
consequently the terms multiplied by
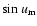 will disappear.
will disappear.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{h4008f2a.eps}\hspace*{2mm}
\...
...e.eps}\hspace*{2mm}
\includegraphics[width=7.5cm,clip]{h4008f2f.eps}\end{figure}](/articles/aa/full/2003/06/aah4008/Timg113.gif) |
Figure 2:
The long period dinamical contribution of O-Cs calculated by numerical integration,
furthermore, with the analytical formulae presented in this paper, and in
Mayer (1990). Upper panels: low mutual inclinations. Middle panels: medium mutual inclinations.
Lower panels: high mutual inclinations. (For the exact input parameters see Tables 2, 3.) |
In order to illustrate the accuracy of our result, and to compare it with the formula of
Mayer (1990) we carried out several numerical integrations with different initial conditions.
The description of the integrator can be found in Borkovits et al. (2002). The only alteration applied here is, that
the sampling of the Jacobian coordinates and velocities is done after the integration step closest to
the center of an eclipse, and not to the vicinity of the periastron. Only mass-point
approximation was applied. As initial parameters the physical properties and orbital elements of two
well-known close triple systems were chosen (see Tables 1-3).
As it can well be seen in Fig. 2, in the exact coplanar case (upper left panel), as well as in the case,
when the two orbital planes intersect each other on the plane of the sky (upper right panel) both Mayer's and our
results give similarly accurate approximations, while in the other cases the differences are significant.
Table 1:
The initial parameters of the close systems. (The masses are given in solar mass, the period in days, and the angular
orbital elements in degrees.)
The non-arbitrary parameters are taken from Söderhjelm (1980), Lestrade et al. (1993) for Algol,
and from Drechsel et al. (1994) for IU Aur.
| System |
m1 |
m2 |
P |
e |
i |
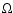 |
u |
| "Algol AB'' |
3.7 |
0.8 |
2.8673 |
0.0 |
82.3 |
52 |
60 |
| "IU Aur AB'' |
21.3 |
14.4 |
1.811474 |
0.0 |
88.0 |
60 |
90 |
Table 2:
The fixed initial parameters of the wide systems. The mass function f(m3) is calculated from the amplitude of the O-C curve, and is given in solar mass. The period P' is given in days, while the periastron passage 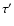 in HJD-2 400 000.
in HJD-2 400 000.
| System |
f(m3) |
P' |
e' |
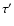 |
| "Algol AB-C'' |
0.125 |
679.9 |
0.23 |
50 000.0 |
| "IU Aur AB-C'' |
1.89 |
294 |
0.54a |
50 000.0 |
a In the (last) run I10 e'=0.24 was chosen. (See text for details.)


Up: On the detectability of
Copyright ESO 2003
![\begin{figure}
\par\includegraphics[width=12cm,clip]{h4008f1.eps}\end{figure}](/articles/aa/full/2003/06/aah4008/Timg7.gif)
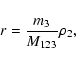
![]() the elapsed time between the ith and the (i+1)th eclipsing
(let's say primary) minima. (Hereafter we refer to
the elapsed time between the ith and the (i+1)th eclipsing
(let's say primary) minima. (Hereafter we refer to
![]() as eclipsing period.) Then it can be seen easily that
as eclipsing period.) Then it can be seen easily that
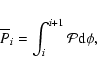
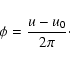
![]() as
as
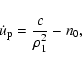
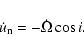
![]() component on the instantaneous period. It can be easily seen, that
component on the instantaneous period. It can be easily seen, that
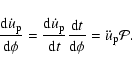
![$\displaystyle \left[(e\cos\omega)_0+\int_0^\phi\frac{{\rm d}}{{\rm d}\phi}(e\cos\omega){\rm d}\phi'\right]\sin{u}(\phi)$](/articles/aa/full/2003/06/aah4008/img80.gif)
![$\displaystyle -\left[(e\sin\omega)_0+\int_0^\phi\frac{{\rm d}}{{\rm d}\phi}(e\sin\omega){\rm d}\phi'\right]\cos{u}(\phi),$](/articles/aa/full/2003/06/aah4008/img81.gif)
![]() function.
As it is well known
function.
As it is well known
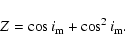
![\begin{figure}
\par\includegraphics[width=8cm,clip]{h4008f2a.eps}\hspace*{2mm}
\...
...e.eps}\hspace*{2mm}
\includegraphics[width=7.5cm,clip]{h4008f2f.eps}\end{figure}](/articles/aa/full/2003/06/aah4008/Timg113.gif)