

Up: On the detectability of
In this paper we examined the possibility of detecting certain kind of perturbations, which are manifesting
themselves on a very short time scale (even during a yearly observing window of the eclipsing variable),
but usually omitted due to their low amplitude. This question naturally has different aspects. These are as follows:
- There are only a few known systems where the amplitude of the dynamical term in the O-C exceeds
significantly the present observational accuracy. We can easily estimate the maximum-value
of the P'/P ratio which is necessary to fulfill this condition. Supposing that the three components have
equal masses, and the third body revolves in a circular orbit, according to Eq. (72) the amplitude may exceed the
10-3 day limit, if P'/P<40P, at least when the two orbits are perpendicular to each other. If the outer orbit
has significant eccentricity (say e'=0.50), or the system consists of stars with different masses, then this limit
in the function of the mutual inclination may even grow up to
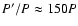 .
From that point of view
the two systems for which the numerical integrations were carried out in this paper are placed near the
limit of the detectability, as for Algol
.
From that point of view
the two systems for which the numerical integrations were carried out in this paper are placed near the
limit of the detectability, as for Algol
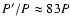 ,
while for IU Aur the same value is
,
while for IU Aur the same value is
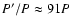 .
.
The three presently known closest eclipsing triple systems are 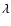 Tau (
Tau (
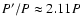 ),
DM Per (
),
DM Per (
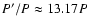 ), and VV Ori (
), and VV Ori (
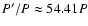 )
(see e.g. the catalogue of Chambliss 1992). In the cases of the latter two binaries unfortunately only a very
few times of minima observations can be found in the literature, although we could expect the largest
effects at these stars. On the other hand, we have to note that as the amplitude of the light time-effect decreases with P'2/3,
at these stars already the detection of the pure geometrical effect is also a challenge. In the most interesting case
of
)
(see e.g. the catalogue of Chambliss 1992). In the cases of the latter two binaries unfortunately only a very
few times of minima observations can be found in the literature, although we could expect the largest
effects at these stars. On the other hand, we have to note that as the amplitude of the light time-effect decreases with P'2/3,
at these stars already the detection of the pure geometrical effect is also a challenge. In the most interesting case
of 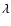 Tau, the amplitude of the perturbative terms may be larger with an order of magnitude than
that of the light-time terms. Furthermore, at this system due to the large amount of proximity our initial assumptions
may loose their validity.
Tau, the amplitude of the perturbative terms may be larger with an order of magnitude than
that of the light-time terms. Furthermore, at this system due to the large amount of proximity our initial assumptions
may loose their validity.
- The second aspect is mainly a technical question. It refers to the observing strategy. This was written already
in the conclusion of Borkovits et al. (2002), but, for the sake of the completeness, we repeat it. In order to have any
chance for the detection of this phenomenon frequent and accurate timings are necessary. It is desirable to
cover a few revolutions of the distant object as densely as possible. The shorter the time interval of such coverage,
the smaller the apse-node time scale or secular variations in the orbital elements which could modify the results.
- Finally, the mathematical modelling of perturbations are necessary in order to extract all information
from the observations.
In this paper we concentrated mainly on this third item. We calculated a new analytical formula
which gives the long period perturbations of the times of minima in eclipsing binaries.
We found that this formula is very similar to the earlier expression of Mayer (1990), nevertheless, some
errors are corrected. Using this expression we developed a numerical method to separate this dynamical effect from
the pure geometrical light time effect. We tested the capabilities of our model by the analysis of numerically simulated
O-C curves. In the case of the test runs for outer orbits with moderate eccentricity, significantly better
solutions were found than in the larger eccentricity cases.
Naturally the next step would be the application of the method for observed O-C diagrams of real systems. Unfortunately,
up to now there are not any O-C diagrams with sufficient accuracy for the possible target systems. This is why
we plan to observe some of the few such systems in the near future to collect as many new times of minima as possible.


Up: On the detectability of
Copyright ESO 2003
![]() Tau (
Tau (
![]() ),
DM Per (
),
DM Per (
![]() ), and VV Ori (
), and VV Ori (
![]() )
(see e.g. the catalogue of Chambliss 1992). In the cases of the latter two binaries unfortunately only a very
few times of minima observations can be found in the literature, although we could expect the largest
effects at these stars. On the other hand, we have to note that as the amplitude of the light time-effect decreases with P'2/3,
at these stars already the detection of the pure geometrical effect is also a challenge. In the most interesting case
of
)
(see e.g. the catalogue of Chambliss 1992). In the cases of the latter two binaries unfortunately only a very
few times of minima observations can be found in the literature, although we could expect the largest
effects at these stars. On the other hand, we have to note that as the amplitude of the light time-effect decreases with P'2/3,
at these stars already the detection of the pure geometrical effect is also a challenge. In the most interesting case
of ![]() Tau, the amplitude of the perturbative terms may be larger with an order of magnitude than
that of the light-time terms. Furthermore, at this system due to the large amount of proximity our initial assumptions
may loose their validity.
Tau, the amplitude of the perturbative terms may be larger with an order of magnitude than
that of the light-time terms. Furthermore, at this system due to the large amount of proximity our initial assumptions
may loose their validity.