As it was mentioned in Sect. 3, the following eight parameters can be adjusted in our
non-linear Levenberg-Marquardt code: c0, P,
![]() ,
e',
,
e', ![]() ,
l'0, i',
,
l'0, i',
![]() .
Here we list the analytical form of the partial derivatives of the Fourier-coefficients with respect to these parameters. The ak, bk symbols refer to the
coefficients of the geometrical light-time effect, while a*k, b*k denote the dynamical terms.
(We note that in the following:
.
Here we list the analytical form of the partial derivatives of the Fourier-coefficients with respect to these parameters. The ak, bk symbols refer to the
coefficients of the geometrical light-time effect, while a*k, b*k denote the dynamical terms.
(We note that in the following:
![]() ,
,
![]() .)
.)
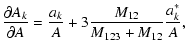 |
(A.1) | ||
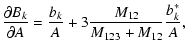 |
(A.2) | ||
![$\displaystyle \frac{\partial{A_1}}{\partial{e'}}=-A\frac{e'}{2}\left[\frac{3}{2}\cos\left(l'_0+\omega'\right)+\cos\omega'\cos{l'_0}\right]+\frac{a^*_1}{e'},$](/articles/aa/full/2003/06/aah4008/img180.gif) |
(A.3) | ||
![$\displaystyle \frac{\partial{B_1}}{\partial{e'}}=-A\frac{e'}{2}\left[\frac{3}{2}\sin\left(l'_0+\omega'\right)+\cos\omega'\sin{l'_0}\right]+\frac{b^*_1}{e'},$](/articles/aa/full/2003/06/aah4008/img181.gif) |
(A.4) | ||
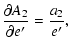 |
(A.5) | ||
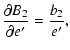 |
(A.6) | ||
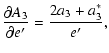 |
(A.7) | ||
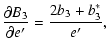 |
(A.8) | ||
![$\displaystyle \frac{\partial a_1}{\partial\omega'}=A\left[\left(A.1-\frac{3e'^2}{8}\right)\sin\left(l'_0+\omega'\right)-\frac{e'^2}{4}\sin\omega'\cos{l'_0}\right],$](/articles/aa/full/2003/06/aah4008/img186.gif) |
(A.9) | ||
![$\displaystyle \frac{\partial b_1}{\partial\omega'}=-A\left[\left(A.1-\frac{3e'^2}...
...right)\cos\left(l'_0+\omega'\right)+\frac{e'^2}{4}\sin\omega'\sin{l'_0}\right],$](/articles/aa/full/2003/06/aah4008/img187.gif) |
(A.10) | ||
![$\displaystyle \frac{\partial a^*_1}{\partial\omega'}=-2A^*e'\left[{\cal{C}}\cos\left(l'_0+2\omega'\right)+{\cal{S}}\sin\left(l'_0+2\omega'\right)\right],$](/articles/aa/full/2003/06/aah4008/img188.gif) |
(A.11) | ||
![$\displaystyle \frac{\partial b^*_1}{\partial\omega'}=2A^*e'\left[{\cal{S}}\cos\left(l'_0+2\omega'\right)-{\cal{C}}\sin\left(l'_0+2\omega'\right)\right],$](/articles/aa/full/2003/06/aah4008/img189.gif) |
(A.12) | ||
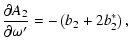 |
(A.13) | ||
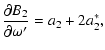 |
(A.14) | ||
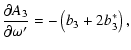 |
(A.15) | ||
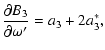 |
(A.16) | ||
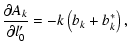 |
(A.17) | ||
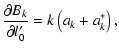 |
(A.18) | ||
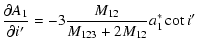 |
|||
| (A.19) | |||
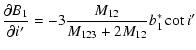 |
|||
| (A.20) | |||
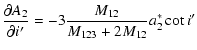 |
|||
| (A.21) | |||
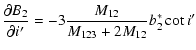 |
|||
| (A.22) | |||
 |
|||
 |
|||
| (A.23) | |||
 |
|||
 |
|||
| (A.24) | |||
![$\displaystyle \frac{\partial A_1}{\partial D}=2A^*e'\big\{I_1\left[6\cos{l'_0}-\cos\left(l'_0+2\omega'\right)\right]-I_2\sin\left(l'_0+2\omega'\right)$](/articles/aa/full/2003/06/aah4008/img214.gif) |
|||
| (A.25) | |||
![$\displaystyle \frac{\partial B_1}{\partial D}=2A^*e'\big\{I_1\left[6\sin{l'_0}-\sin\left(l'_0+2\omega'\right)\right]+I_2\cos\left(l'_0+2\omega'\right)$](/articles/aa/full/2003/06/aah4008/img216.gif) |
|||
| (A.26) | |||
![$\displaystyle \frac{\partial A_2}{\partial D}=2b^*_2\cos{i'}+2A^*\left[I_1\cos2\left(l'_0+\omega'\right)+I_2\sin2\left(l'_0+\omega'\right)\right],$](/articles/aa/full/2003/06/aah4008/img218.gif) |
|||
| (A.27) | |||
![$\displaystyle \frac{\partial B_2}{\partial D}=-2a^*_2\cos{i'}+2A^*\left[I_1\sin2\left(l'_0+\omega'\right)-I_2\cos2\left(l'_0+\omega'\right)\right],$](/articles/aa/full/2003/06/aah4008/img219.gif) |
|||
| (A.28) | |||
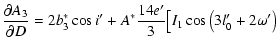 |
|||
| (A.29) | |||
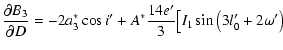 |
|||
| (A.30) |
| (A.31) | |||
| (A.32) |
Acknowledgements
We thank Dr. László Szabados and Mr. Szilárd Csizmadia for their comments on the manuscript, as well as Mrs. Rita Borkovits-József and Mr. Imre Barna Bíró for the linguistic corrections. This research has made use of NASA's Astrophysics Data System Bibliographic Services.
Copyright ESO 2003