

Up: From clouds to stars
Subsections
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{lgL_lgAge_MMLtrack.eps} \end{figure}](/articles/aa/full/2003/06/aa8963/Timg62.gif) |
Figure 2:
The relation between age and luminosity for the collapse of
Bonnor-Ebert spheres ( full lines) and classical, fully hydrostatic
models of pre-main sequence evolution. These relations are relevant for
the determination of PMS-ages. For the comparison we use the
quasi-hydrostatic results by D'Antona & Mazzitelli (1994)
("Alexander + MLT'' case) for
0.1, 0.5, 1 and
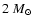 ( dotted lines from left to right). Classical PMS-models
do not accrete and evolve at constant mass. The new PMS-ages
calculated from the collapse of cloud fragments are larger than the
classical values by up to a Myr, depending on luminosity. This
is due to an age offset because the formation process is modeled
and due to a different PMS-contraction behaviour caused by the
difference between the assumed initial thermal structure in classical
tracks and the thermal structure calculated from the collapse and
accretion process.
Note that collapse luminosities show an initial rise, close to
zero age, as the protostars are "switched'' on after core formation.
Ages inferred using collapse PMS-tracks will be larger than those
inferred from classical tracks by up to a Myr at ages below 2 Myr.
The dashed and dash-dotted line, close to the
( dotted lines from left to right). Classical PMS-models
do not accrete and evolve at constant mass. The new PMS-ages
calculated from the collapse of cloud fragments are larger than the
classical values by up to a Myr, depending on luminosity. This
is due to an age offset because the formation process is modeled
and due to a different PMS-contraction behaviour caused by the
difference between the assumed initial thermal structure in classical
tracks and the thermal structure calculated from the collapse and
accretion process.
Note that collapse luminosities show an initial rise, close to
zero age, as the protostars are "switched'' on after core formation.
Ages inferred using collapse PMS-tracks will be larger than those
inferred from classical tracks by up to a Myr at ages below 2 Myr.
The dashed and dash-dotted line, close to the
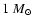 -relation, are obtained by changing the mixing length
parameter -relation, are obtained by changing the mixing length
parameter
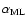 to 1.2 and 1.4, respectively, for the same
fragment mass, see text.
to 1.2 and 1.4, respectively, for the same
fragment mass, see text.
|
In this section we discuss the results for the collapse of
critical Bonnor-Ebert spheres with a temperature of 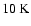 and masses of 0.05 to
and masses of 0.05 to
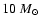 within a constant volume, as
obtained by the methods described above. For a description of the
method of solution we refer to Appendix B.
within a constant volume, as
obtained by the methods described above. For a description of the
method of solution we refer to Appendix B.
The results described below are quantities derived from the flows
which are obtained as the solution of equations given in
Table .1, for the Bonnor-Ebert collapses.
Since there is no a priori hydrostatic part and no a priori photospheric
model in our model (they result as special properties of the solutions of
our flow equations) we describe how the stellar parameters age,
effective temperature, radii and masses are obtained from the radiation
hydrodynamical flows. We restrict our discussion mostly to these basic
parameters to give an overview over the collapse solutions. We start our
discussion with a proposal for the definition of zero stellar age, because
as it turns out that most our definitions of stellar parameters will only
be valid after this instant of time.
The modeling of the star formation process together with the
PMS-contraction opens up the possibility to define a stellar zero age.
We require the instant of age zero to be
(1), well defined,
(2), a unique clock for an individual star; it should be reset by
a destruction of the star and stellar mergers, and
(3), the gravitationally weakly bound, tenuous states of the cloud should
not contribute to stellar age - a long-lasting quasi-static cloud phase
would otherwise induce almost arbitrary age additions without any
consequences for the subsequent evolution.
To compare the luminosities of objects of various masses at a given age
a general definition of zero age is necessary. As the thermally
controlled Kelvin-Helmholtz contraction is the dominating evolutionary
process in young gas spheres, whether they are giant planets, brown dwarfs
or stars, we propose to use as age zero the instant of time, when the
interior of the gas spheres is thermally enclosed for the first time.
The enclosure means that photons
cannot escape from the entire object directly
but are radiated from a photosphere.
Energy transfer to the photospheric bottleneck then
delays the cooling and determines how the thermal reservoir in the
interior is emptied. The cooling history can then be used to define an
age since the heat reservoir was formed. As a practical
definition for age zero we propose to use the instant of time
when the Rosseland mean optical depth of a gaseous object equals 2/3, i.e.,
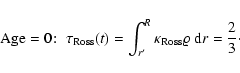 |
(1) |
We use 2/3 here because of the advantage for, e.g., the
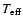 definition
in the comparison to D'Antona &
Mazzitelli (1994) but recommend to use
definition
in the comparison to D'Antona &
Mazzitelli (1994) but recommend to use
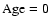 at
at
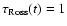 ,
in general.
,
in general. 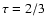 results from an averaging of optical depth over the stellar
disk that is specific to the grey Eddington approximation.
results from an averaging of optical depth over the stellar
disk that is specific to the grey Eddington approximation.
For a protostar this instant of time is practically at the end of the
isothermal phase of the collapse. Furthermore, with definition (1)
the luminosities of the protoplanets can be compared to stars and brown
dwarfs of similar age.
The proposed definition of zero age has the following properties:
(1), it preceeds the short phase of the "final hydrostatic
core formation'' for protostars that was used in earlier work
(Appenzeller & Tscharnuter 1975; Winkler & Newman 1980a)
by only 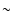
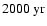 .
It corresponds to the sharp
initial luminosity rise
(within 1000 yr for 0.05 to 10
.
It corresponds to the sharp
initial luminosity rise
(within 1000 yr for 0.05 to 10 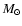 )
that occurs
when the first (molecular hydrogen) protostellar cores form.
Because this happens during this rapid dynamical density enhancement
due to early cloud collapse, the proposed definition is very sharp,
in the sense that the properties
of the cloud vary rapidly in the vicinity of zero age;
)
that occurs
when the first (molecular hydrogen) protostellar cores form.
Because this happens during this rapid dynamical density enhancement
due to early cloud collapse, the proposed definition is very sharp,
in the sense that the properties
of the cloud vary rapidly in the vicinity of zero age;
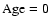 is reached during a phase of rapid changes in the observables. As a
consequence it will be observationally well defined;
(2), it is "close'' to the formation time of the oldest "rocks'' in the
solar system. They presumably form during the process of planetesimal
formation that occurs according to present understanding within
is reached during a phase of rapid changes in the observables. As a
consequence it will be observationally well defined;
(2), it is "close'' to the formation time of the oldest "rocks'' in the
solar system. They presumably form during the process of planetesimal
formation that occurs according to present understanding within
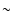
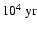 after pre-planetary nebula formation. The pre-planetary
nebula forms roughly at the time when the final hydrostatic protostellar
core settles into hydrostatic equilibrium (Tscharnuter 1987).
Hence, together with the
after pre-planetary nebula formation. The pre-planetary
nebula forms roughly at the time when the final hydrostatic protostellar
core settles into hydrostatic equilibrium (Tscharnuter 1987).
Hence, together with the 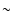
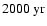 for final core formation,
the ages of the oldest meteorites and meteoritic components that
are determined by
absolute radioactive dating should be only
for final core formation,
the ages of the oldest meteorites and meteoritic components that
are determined by
absolute radioactive dating should be only 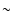
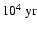 smaller than the ages defined here. This results in a conceptual consistency
of our ages and the meteoritic ages to within probably <
smaller than the ages defined here. This results in a conceptual consistency
of our ages and the meteoritic ages to within probably <
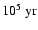 .
It is a useful property because solar system ages of
.
It is a useful property because solar system ages of
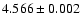 Gyr
(Allègre et al. 1995; for Allende CAIs) are
used to calibrate stellar structure theory by assuming that the age of the
Sun is equal to the age of the meteorites and a comparison of
stellar-evolution models of the Sun at theoretical ages with properties
of the present Sun;
(3), relative ages of different objects in a star formation region
are physically well defined;
(4), the thermal clock which is based on the dominating dynamical process
in early stellar evolution, namely gravitational contraction and
cooling is (re)set at the proposed zero age;
(5), the age spread in young clusters is conceptually accessible without
reference to the ZAMS, and knowledge about it. Concepts involving the
ZAMS rely on the assumption that it will be reached. This is not
guaranteed as it does not exist for brown dwarfs and planets. Hence
such concepts would be inapplicable for those objects.
Our proposed zero age is a well defined concept for all masses at least
from an earth mass up to the largest stellar masses;
(6), questions about coevolution of very young binaries can be addressed
because individual component ages are well defined;
(7), with this zero age we use the earliest instant when an effective
temperature can be defined, based on a radius defined by using
optical depth.
With age definition (1) we can study the luminosity emitted by our
cloud volume as a function of age. In the beginning the luminosity comes
from the still almost isothermal cloud fragment, in the end from the
pre-main sequence star that has formed in the centre. We will use this
age to discuss the effect of the cloud collapse on pre-main sequence
ages. We can expect two main effects relative to hydrostatic models
of early stellar evolution: (i) an age offset that is due to
the fact that the collapse phase which is not modeled in fully hydrostatic
PMS-studies adds contributions of the order of a free-fall time
to the ages usually given (see Tables 1, 2),
and (ii) an effect due to the different PMS-contraction behaviour that
is due to the difference between the assumed initial thermal structure
of classical PMS-calculations and the thermal structure as calculated
from the collapse and accretion process in this work.
Gyr
(Allègre et al. 1995; for Allende CAIs) are
used to calibrate stellar structure theory by assuming that the age of the
Sun is equal to the age of the meteorites and a comparison of
stellar-evolution models of the Sun at theoretical ages with properties
of the present Sun;
(3), relative ages of different objects in a star formation region
are physically well defined;
(4), the thermal clock which is based on the dominating dynamical process
in early stellar evolution, namely gravitational contraction and
cooling is (re)set at the proposed zero age;
(5), the age spread in young clusters is conceptually accessible without
reference to the ZAMS, and knowledge about it. Concepts involving the
ZAMS rely on the assumption that it will be reached. This is not
guaranteed as it does not exist for brown dwarfs and planets. Hence
such concepts would be inapplicable for those objects.
Our proposed zero age is a well defined concept for all masses at least
from an earth mass up to the largest stellar masses;
(6), questions about coevolution of very young binaries can be addressed
because individual component ages are well defined;
(7), with this zero age we use the earliest instant when an effective
temperature can be defined, based on a radius defined by using
optical depth.
With age definition (1) we can study the luminosity emitted by our
cloud volume as a function of age. In the beginning the luminosity comes
from the still almost isothermal cloud fragment, in the end from the
pre-main sequence star that has formed in the centre. We will use this
age to discuss the effect of the cloud collapse on pre-main sequence
ages. We can expect two main effects relative to hydrostatic models
of early stellar evolution: (i) an age offset that is due to
the fact that the collapse phase which is not modeled in fully hydrostatic
PMS-studies adds contributions of the order of a free-fall time
to the ages usually given (see Tables 1, 2),
and (ii) an effect due to the different PMS-contraction behaviour that
is due to the difference between the assumed initial thermal structure
of classical PMS-calculations and the thermal structure as calculated
from the collapse and accretion process in this work.
In our discussion, we use the relation between luminosity and age
for two reasons: (1) because of the uncertainties (both theoretical
and observational)
in the determination of the effective temperature of objects in the vicinity
of the Hayashi-tracks, and (2) because these tracks are very steep in the
HRD during the early PMS evolution - the luminosity decreases at
almost constant effective temperature. These relations for the collapse
of Bonnor-Ebert spheres of 0.1, 0.5, 1 and
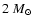 are depicted
in
Fig. 2. The relations determined from collapse (full lines)
originate from zero luminosity, i.e., before the cloud fragment starts to radiate
significantly. The fully hydrostatic relations (dotted lines) begin at an
assumed initial age and at a luminosity that is the consequence of the assumed
(usually fully convective, or n=3/2 polytrope) initial thermal structure.
are depicted
in
Fig. 2. The relations determined from collapse (full lines)
originate from zero luminosity, i.e., before the cloud fragment starts to radiate
significantly. The fully hydrostatic relations (dotted lines) begin at an
assumed initial age and at a luminosity that is the consequence of the assumed
(usually fully convective, or n=3/2 polytrope) initial thermal structure.
Notice the age offset of about
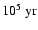 ,
about a free-fall time,
between the beginning of the classical and collapse curves in all cases.
This is due to the assumed initial ages of fully hydrostatic calculations.
Next we look at the possibility of attributing all the differences to an age
offset. This could be done by shifting the classical curves upward to
higher ages until the luminosities match the new curves. Such a procedure
could be considered successful if the rates of change in luminosity of
classical and collapse L(t)-relations match, too. This would be
indicated by the luminosity difference between corresponding old and
new relations of the same mass to be constant.
For the
,
about a free-fall time,
between the beginning of the classical and collapse curves in all cases.
This is due to the assumed initial ages of fully hydrostatic calculations.
Next we look at the possibility of attributing all the differences to an age
offset. This could be done by shifting the classical curves upward to
higher ages until the luminosities match the new curves. Such a procedure
could be considered successful if the rates of change in luminosity of
classical and collapse L(t)-relations match, too. This would be
indicated by the luminosity difference between corresponding old and
new relations of the same mass to be constant.
For the
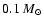 case this is fairly successful and the
collapse may be essentially viewed as producing an age offset of about
case this is fairly successful and the
collapse may be essentially viewed as producing an age offset of about
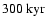 .
For the other masses this procedure does not hold.
Even for the
.
For the other masses this procedure does not hold.
Even for the
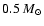 relations an addition of
relations an addition of
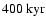 to the classical relation might just bring the luminosities in accord, but
the relations still diverge because of the different contraction behaviour.
to the classical relation might just bring the luminosities in accord, but
the relations still diverge because of the different contraction behaviour.
The consequences for the inferred ages at given luminosity are already
considerable for
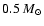 :
at the end of the collapse
calculation, a PMS-object with solar luminosity has a new
age of
:
at the end of the collapse
calculation, a PMS-object with solar luminosity has a new
age of
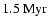 while following down the
while following down the
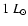 -ordinate
to the classical tracks gives
-ordinate
to the classical tracks gives
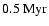 .
The situation is very similar
for
the 1 and
.
The situation is very similar
for
the 1 and
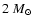 clouds, but the differences in luminosity evolution to
the classical relations are even more pronounced. Changing the mixing length,
a procedure that probably produces the largest changes in classical models
does not significantly change this conclusion. This can be seen by comparing
the dashed and dash-dotted lines, for
clouds, but the differences in luminosity evolution to
the classical relations are even more pronounced. Changing the mixing length,
a procedure that probably produces the largest changes in classical models
does not significantly change this conclusion. This can be seen by comparing
the dashed and dash-dotted lines, for
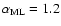 and 1.4, respectively,
that are very close to the standard 1
and 1.4, respectively,
that are very close to the standard 1 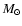 collapse relation for
collapse relation for
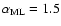 .
.
Next the adopted age definition allows us to define the "stellar'' properties,
i.e., the properties of the optically thick, ultimately hydrostatic parts of
the flow for any instant after zero age. This is described in the next
section.
Here we focus on the observables of the collapsing cloud fragments and the
resulting young stars, so we define our stellar radii to be the
optical depth radii, 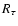 ,
obtained by determining the radius
r' at which
,
obtained by determining the radius
r' at which
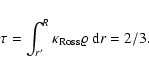 |
(2) |
Because of our definition of zero age such a radius exists.
This is not necessarily close to the density radius, 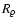 ,
i.e., the location of the maximum
absolute value of the density gradient, that usually defines the
stellar radius (density gradients in shocks are ignored for this procedure
cf. Winkler & Newman 1980a,b; Baschek et al. 1991). Note that Balluch
(1991a-c) used the radius of the accretion shock as an estimate for
,
i.e., the location of the maximum
absolute value of the density gradient, that usually defines the
stellar radius (density gradients in shocks are ignored for this procedure
cf. Winkler & Newman 1980a,b; Baschek et al. 1991). Note that Balluch
(1991a-c) used the radius of the accretion shock as an estimate for
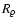 and the stellar radius,
which is a good estimate due to the small stand-off distance of the shock.
and the stellar radius,
which is a good estimate due to the small stand-off distance of the shock.
The optical depth radius gives a measure of the radius
from which the photons escape and which parts of the flow are thermally
shielded from the outside. It is the length scale a (bolometric) observer
would see. It is very close to the density radius once the protostellar
cocoon has been sufficiently diluted by accretion to make it transparent
down to the stellar photosphere. The two radii converge when
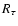 "jumps'' from the dust photosphere to the stellar photosphere
and intercepts
"jumps'' from the dust photosphere to the stellar photosphere
and intercepts 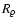 .
.
With the luminosity at the outer boundary and the optical depth radius
we determine an effective temperature by
 |
(3) |
The so defined
 -values are used in our Hertzsprung-Russell
diagrams. To give an estimate for the uncertainty involved when placing a
protostar into the Hertzsprung-Russell diagram we additionally
plot two alternative
temperature definitions in Fig. 1:
(1) a temperature T(RT)based on the temperature radius, RT,
that is governed by
-values are used in our Hertzsprung-Russell
diagrams. To give an estimate for the uncertainty involved when placing a
protostar into the Hertzsprung-Russell diagram we additionally
plot two alternative
temperature definitions in Fig. 1:
(1) a temperature T(RT)based on the temperature radius, RT,
that is governed by
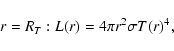 |
(4) |
cf. Baschek et al. (1991). This is the temperature at a distinct
point in the flow where the luminosity corresponds to the value
that would be obtained by
a blackbody radiating at the local flow matter-temperature.
(2) a photospheric temperature defined by
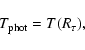 |
(5) |
i.e., the local flow temperature at the optical depth radius. It is a measure
of the temperature at the location from which the photons typically escape
towards an observer.
In a static, compact, radiative photosphere in Eddington approximation,
the definitions result in the same temperatures (cf. Baschek et al. 1991).
The resulting theoretical Hertzsprung-Russell diagram for the collapse of
a
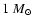 Bonnor-Ebert sphere is shown in Fig. 1.
In this case the mixing length parameter
Bonnor-Ebert sphere is shown in Fig. 1.
In this case the mixing length parameter
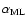 is chosen to
be 1.4 to facilitate
the comparison with the fully hydrostatic pre-main sequence calculation.
The thick line shows the evolutionary track in the Hertzsprung-Russell diagram
by using the effective temperature based on the optical depth radius
is chosen to
be 1.4 to facilitate
the comparison with the fully hydrostatic pre-main sequence calculation.
The thick line shows the evolutionary track in the Hertzsprung-Russell diagram
by using the effective temperature based on the optical depth radius 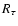 (as used in earlier collapse studies by Appenzeller & Tscharnuter 1975 and
Winkler & Newman 1980a). The track starts at the instant of zero age, indicated
by the diamond symbol. As above noted the adopted definition of zero age coincides
with the first instant at which the effective temperature concept can be used.
(as used in earlier collapse studies by Appenzeller & Tscharnuter 1975 and
Winkler & Newman 1980a). The track starts at the instant of zero age, indicated
by the diamond symbol. As above noted the adopted definition of zero age coincides
with the first instant at which the effective temperature concept can be used.
The initial decrease in
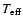 is due to the fact that by definition
is due to the fact that by definition
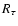 starts out very small but rapidly increases during the first core
formation. This occurs because the core's density and optical depth increase
rapidly during this settling into hydrostatic equilibrium.
starts out very small but rapidly increases during the first core
formation. This occurs because the core's density and optical depth increase
rapidly during this settling into hydrostatic equilibrium. 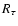 increases
at approximately constant luminosity and hence
increases
at approximately constant luminosity and hence
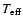 drops.
Temperatures given before zero age
(dash-dotted part) are central temperatures of the still transparent,
almost isothermal cloud. With the onset of accretion onto the
core the luminosity rises sharply with a moderate increase in
drops.
Temperatures given before zero age
(dash-dotted part) are central temperatures of the still transparent,
almost isothermal cloud. With the onset of accretion onto the
core the luminosity rises sharply with a moderate increase in
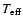 .
The "mouse-head'' is the hall mark of the formation of the second (inner)
atomic hydrogen core that forms after the (second) collapse of the
dissociating molecular hydrogen core. At the cusp after the first luminosity
maximum the final accretion phase is entered. As the luminosity rises towards
the second maximum, the first core is accreted onto the second one and the
Mach numbers of the flow increase above ten. The small luminosity decrease
after the second maximum accompanies the adjustment of the accretion flow
and the mass accretion rate onto the final core to the substantial luminosity
now radiated from the accretion shock.
.
The "mouse-head'' is the hall mark of the formation of the second (inner)
atomic hydrogen core that forms after the (second) collapse of the
dissociating molecular hydrogen core. At the cusp after the first luminosity
maximum the final accretion phase is entered. As the luminosity rises towards
the second maximum, the first core is accreted onto the second one and the
Mach numbers of the flow increase above ten. The small luminosity decrease
after the second maximum accompanies the adjustment of the accretion flow
and the mass accretion rate onto the final core to the substantial luminosity
now radiated from the accretion shock.
When the luminosity starts rising
again the quasi-steady main-accretion phase commences. Shortly after the flat
top part of the track is reached, the luminosity, due to
D burning, becomes significant and reaches a maximum of 60% at the
global luminosity maximum.
When the volume is significantly depleted by the accretion process the
luminosity starts decreasing and
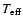 rises as parts of the flow
closer to the young star become visible. When the dust cocoon becomes transparent
the optical depth radius "jumps'' into the "stellar'' photosphere the effective
temperature sharply increases, crosses the classical PMS-track, the
Hayashi line and finally reaches the "corner'' of the collapse track, at maximum
rises as parts of the flow
closer to the young star become visible. When the dust cocoon becomes transparent
the optical depth radius "jumps'' into the "stellar'' photosphere the effective
temperature sharply increases, crosses the classical PMS-track, the
Hayashi line and finally reaches the "corner'' of the collapse track, at maximum
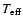 .
From this point on
.
From this point on
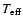 coincides with the temperature
definition based on the temperature radius (thick and dashed line
overlap).
coincides with the temperature
definition based on the temperature radius (thick and dashed line
overlap).
Hence the radiation hydrodynamical results for temperature based on
RT and 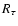 converge to the equality valid in classical, hydrostatic
photospheres. The photospheric
temperature (dotted) at
converge to the equality valid in classical, hydrostatic
photospheres. The photospheric
temperature (dotted) at  passes the shock at this instant and
produces
a sharp spike to the left as
passes the shock at this instant and
produces
a sharp spike to the left as  is at the peak temperature
just downstream from the accretion shock, and still upstream from
the radiative relaxation layer. As the
accretion luminosity becomes negligibly small and after "D burnout'' the collapse
track turns almost parallel to the classical track, slightly pointing towards
the ZAMS location of the Sun on the classical track. The photospheric
temperature remains different from the other two temperatures, and slightly
cooler than the
is at the peak temperature
just downstream from the accretion shock, and still upstream from
the radiative relaxation layer. As the
accretion luminosity becomes negligibly small and after "D burnout'' the collapse
track turns almost parallel to the classical track, slightly pointing towards
the ZAMS location of the Sun on the classical track. The photospheric
temperature remains different from the other two temperatures, and slightly
cooler than the
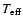 value of the fully hydrostatic classical track.
Note that the photosphere of the collapse calculation is convective all along
the Hayashi-part of the track and
value of the fully hydrostatic classical track.
Note that the photosphere of the collapse calculation is convective all along
the Hayashi-part of the track and
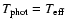 ,
valid for a compact,
hydrostatic, radiative photosphere in Eddington approximation
is not guaranteed under these conditions.
,
valid for a compact,
hydrostatic, radiative photosphere in Eddington approximation
is not guaranteed under these conditions.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{hrd_m_track_lglt_big.eps} \end{figure}](/articles/aa/full/2003/06/aa8963/Timg87.gif) |
Figure 3:
Evolutionary tracks in the Hertzsprung-Russell diagram for the
collapse and early pre-main sequence evolution of 0.05, 0.1, 0.5, 1, 2
and
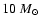 cloud fragments ( full lines).
The dashed lines indicate isochrones for the collapse tracks,
labeled
with the respective ages. Zero age is defined here as the moment when
the respective cloud fragment becomes optically thick and the
interior is
thermally locked as the first photosphere forms (Rosseland mean optical
depth reaches 2/3).
Quasi-hydrostatic tracks for
0.1, 0.5, 1 and
cloud fragments ( full lines).
The dashed lines indicate isochrones for the collapse tracks,
labeled
with the respective ages. Zero age is defined here as the moment when
the respective cloud fragment becomes optically thick and the
interior is
thermally locked as the first photosphere forms (Rosseland mean optical
depth reaches 2/3).
Quasi-hydrostatic tracks for
0.1, 0.5, 1 and
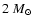 from
D'Antona & Mazzitelli (1994), "Alexander MLT''-case,
from
D'Antona & Mazzitelli (1994), "Alexander MLT''-case,
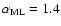 ( dotted lines) are plotted for comparison.
( dotted lines) are plotted for comparison.
|
Keeping in mind the above discussion concerning temperatures we now
proceed to a discussion of evolutionary tracks
for cloud fragments of various masses and the respective isochrones
in the Hertzsprung-Russell diagram, based on the effective temperature with the
optical depth-radius definition (see Baschek et al. 1991 for a discussion,
including the protostellar application).
It is important to note that the isochrones are based on the chosen zero age
and hence the assumption that the first photospheres of all stars have formed at
the same time. Different collapse- and accretion times of fragments of different
masses are included. This is in contrast to hydrostatic studies that count
their ages from an arbitrary zero point related to there initial condition.
In Fig. 3 an
overview over the collapse and PMS evolution of Bonnor-Ebert-sphere
cloud fragments with masses of 0.05, 0.1, 0.5, 1, 2 and
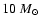 is given. They are compared to classical, non accreting, fully hydrostatic
tracks for 0.1, 0.5, 1, and
is given. They are compared to classical, non accreting, fully hydrostatic
tracks for 0.1, 0.5, 1, and
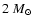 after D'Antona &
Mazzitelli (1994). For the comparison an electronic version of their
"Alexander, MLT''-tracks for
after D'Antona &
Mazzitelli (1994). For the comparison an electronic version of their
"Alexander, MLT''-tracks for
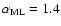 was used.
was used.
The early evolution dominated by the initial cloud collapse is very similar
for all masses. At an age of 1000 yr the first hydrostatic cores form,
with an age spread of a few hundred years. All fragments enter the
main accretion phase at an age slightly above 8 kyr. All tracks remain
below effective temperatures of
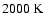 up to
up to
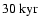 .
The
protostars still remain in
their dust cocoons and radiate from dust photospheres.
The luminosity decline has already started at this
age for the lowest mass fragment. At
.
The
protostars still remain in
their dust cocoons and radiate from dust photospheres.
The luminosity decline has already started at this
age for the lowest mass fragment. At
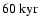 the first object has
arrived on the pre-main sequence, close to the Hayashi track.
It has formed from the lowest mass cloud fragment of
the first object has
arrived on the pre-main sequence, close to the Hayashi track.
It has formed from the lowest mass cloud fragment of
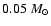 and is a young brown dwarf.
The higher mass fragments follow until the
and is a young brown dwarf.
The higher mass fragments follow until the
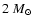 fragment
arrives
on its PMS-track at
fragment
arrives
on its PMS-track at
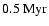 .
The
.
The
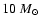 fragment is still
accreting at
fragment is still
accreting at
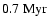 ,
with a hydrostatic central stellar embryo of
,
with a hydrostatic central stellar embryo of
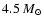 .
.
Figure 3 illustrates that star formation is a
gravitational heating event that increases temperature by about two
orders of magnitude. Due to the negative, so-called gravothermal
specific heat of common, thermally supported self-gravitating systems the
heating slows down when energy
losses slow-down because matter becomes opaque due to the cross-sections
of atoms. Ultimately nuclear energy is added which acts as a long-term
thermostatic effect.
The early PMS evolution of the collapsed cloud fragments shows a relation
to the classical tracks that changes with mass. The
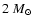 fragment arrives close to the radiative, Henyey part of the corresponding
classical track. The
fragment arrives close to the radiative, Henyey part of the corresponding
classical track. The
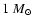 and the
and the
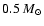 case
arrive on the PMS with a luminosity corresponding to about half way down
on the convective, Hayashi parts
of the classical tracks. The
case
arrive on the PMS with a luminosity corresponding to about half way down
on the convective, Hayashi parts
of the classical tracks. The
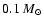 fragment arrives with
a luminosity corresponding to the top of the classical track.
The
fragment arrives with
a luminosity corresponding to the top of the classical track.
The
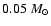 fragment (a proto brown dwarf) is shown to give an
indication of the further mass dependence of the relation to the
fragment (a proto brown dwarf) is shown to give an
indication of the further mass dependence of the relation to the
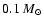 classical track.
For the two lowest masses the age difference can be attributed to an offset
in zero age. Furthermore, D burning has not begun for the
classical track.
For the two lowest masses the age difference can be attributed to an offset
in zero age. Furthermore, D burning has not begun for the
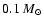 case-as might be expected so close to the brown dwarf limit.
It follows that, by using the appropriate initial thermal structure, this
mass probably will show a quasi-classical PMS evolution starting near
the top of a Hayashi track and a somewhat higher effective temperature,
but, as found in previous studies, with the slow-down of contraction due
to D burning.
case-as might be expected so close to the brown dwarf limit.
It follows that, by using the appropriate initial thermal structure, this
mass probably will show a quasi-classical PMS evolution starting near
the top of a Hayashi track and a somewhat higher effective temperature,
but, as found in previous studies, with the slow-down of contraction due
to D burning.
On the other hand the
results of the collapse calculations indicate substantial corrections
in PMS stellar properties
for masses of
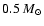 and higher. PMS objects of
these masses already are half-way
in the direction of the Henyey-track when they become visible.
and higher. PMS objects of
these masses already are half-way
in the direction of the Henyey-track when they become visible.
Due to our radiation hydrodynamical approach only the masses of the
cloud fragments are prescribed. The stellar mass and the corresponding
mass accretion rate are calculated from the flow. Hence, quantities like
stellar mass and mass accretion rate are determined
during the evolution of the flow.
For our discussion it is useful to use the optically thick mass, 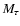 ,
for further considerations. It follows naturally by determining the
mass inside the optical depth radius,
,
for further considerations. It follows naturally by determining the
mass inside the optical depth radius, 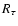 that we have already
used in the definition of
that we have already
used in the definition of
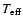 .
This corresponds to the
hydrostatic mass, defined, e.g., via the density radius
(cf. Baschek et al. 1991)
for most of the time but has to be distinguished during the very early
accretion when calculating the accretion-luminosity from
.
This corresponds to the
hydrostatic mass, defined, e.g., via the density radius
(cf. Baschek et al. 1991)
for most of the time but has to be distinguished during the very early
accretion when calculating the accretion-luminosity from
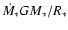 .
We use
.
We use 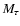 for the remainder.
for the remainder.
In order to show the stellar properties as accretion proceeds we display
lines of constant optically thick mass, 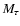 - which we may call
isopleths
- which we may call
isopleths![[*]](/icons/foot_motif.gif) -
in the Hertzsprung-Russell diagram in Fig. 4. It is the actual
stellar mass that determines the stellar properties and not the fragment
mass that includes the entire circumstellar environment under
consideration. The
-
in the Hertzsprung-Russell diagram in Fig. 4. It is the actual
stellar mass that determines the stellar properties and not the fragment
mass that includes the entire circumstellar environment under
consideration. The
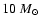 fragment, for example, starts as
the other fragments with
fragment, for example, starts as
the other fragments with
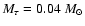 and produces the corresponding
luminosities and effective temperatures despite of its
and produces the corresponding
luminosities and effective temperatures despite of its
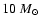 protostellar envelope.
protostellar envelope.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{hrd_m_track_lgLT_meff_big.eps} \end{figure}](/articles/aa/full/2003/06/aa8963/Timg100.gif) |
Figure 4:
Optically thick mass, 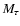 ,
in the Hertzsprung-Russell
diagram for the collapse
and early pre-main sequence evolution of 0.05, 0.1, 0.5, 1, 2
and ,
in the Hertzsprung-Russell
diagram for the collapse
and early pre-main sequence evolution of 0.05, 0.1, 0.5, 1, 2
and
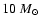 cloud fragments.
cloud fragments. 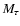 is
the mass interior to the optical depth radius,
is
the mass interior to the optical depth radius, 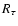 .
Dash-dotted lines are locations of constant .
Dash-dotted lines are locations of constant 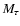 ,
isopleths, with values labelled along
the ,
isopleths, with values labelled along
the
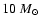 -track.
The locations where -track.
The locations where 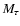 corresponds to 80, 90 and 99% of
the final mass are connected by the thin lines.
The thin line for 99% is used as an estimate for the end of
significant mass accretion. The lines of constant mass are
essentially tangential to the tracks beyond this point.
Quasi-hydrostatic tracks for
0.1, 0.5, 1 and
corresponds to 80, 90 and 99% of
the final mass are connected by the thin lines.
The thin line for 99% is used as an estimate for the end of
significant mass accretion. The lines of constant mass are
essentially tangential to the tracks beyond this point.
Quasi-hydrostatic tracks for
0.1, 0.5, 1 and
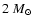 .
(D'Antona & Mazzitelli 1994, "Alexander MLT''-case, .
(D'Antona & Mazzitelli 1994, "Alexander MLT''-case,
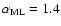 )
are shown for comparison. )
are shown for comparison. |
The lowest isopleth at
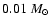 illustrates the fact that hydrostatic
structures of that mass become optically thick (opacity limit of fragmentation)
and, as a consequence, all initial protostellar cores typically form with a
few percent of a solar mass. At
illustrates the fact that hydrostatic
structures of that mass become optically thick (opacity limit of fragmentation)
and, as a consequence, all initial protostellar cores typically form with a
few percent of a solar mass. At
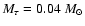 the lowest mass
fragment has almost terminated its main accretion phase while the higher
mass fragments still grow their cores and accelerate their accretion
flows. As
the lowest mass
fragment has almost terminated its main accretion phase while the higher
mass fragments still grow their cores and accelerate their accretion
flows. As 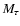 increases to the final mass the isopleths become
tangential to the evolutionary tracks and at constant mass the two
curves are identical. Note the decrease in luminosity when the track of
a fragment approaches an isopleth close to its final mass. The beginning
exhaustion of the mass reservoir becomes then noticeable as a drop in
accretion luminosity.
To mark the end of significant mass accretion, the point at
which 99% of the final mass has been accreted is indicated by
a thin line. For the two smallest masses this happens well before they
reach the Hayashi phase. Accretion, as a consequence, does not play a role
during their PMS-contraction as calculated here. However accretion does
play a role in defining their thermal structure at the "top of the track''.
For masses from
increases to the final mass the isopleths become
tangential to the evolutionary tracks and at constant mass the two
curves are identical. Note the decrease in luminosity when the track of
a fragment approaches an isopleth close to its final mass. The beginning
exhaustion of the mass reservoir becomes then noticeable as a drop in
accretion luminosity.
To mark the end of significant mass accretion, the point at
which 99% of the final mass has been accreted is indicated by
a thin line. For the two smallest masses this happens well before they
reach the Hayashi phase. Accretion, as a consequence, does not play a role
during their PMS-contraction as calculated here. However accretion does
play a role in defining their thermal structure at the "top of the track''.
For masses from
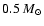 upward the end of significant mass
accretion is terminated after the Hayashi line has been crossed.
upward the end of significant mass
accretion is terminated after the Hayashi line has been crossed.


Up: From clouds to stars
Copyright ESO 2003
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{lgL_lgAge_MMLtrack.eps} \end{figure}](/articles/aa/full/2003/06/aa8963/Timg62.gif)
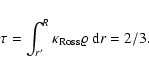
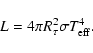
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{hrd_m_track_lglt_big.eps} \end{figure}](/articles/aa/full/2003/06/aa8963/Timg87.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{hrd_m_track_lgLT_meff_big.eps} \end{figure}](/articles/aa/full/2003/06/aa8963/Timg100.gif)