- ... stars
![[*]](/icons/foot_motif.gif)
- Appendices A and B are only available in electronic form at http://www.edpsciences.org
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... almost
![[*]](/icons/foot_motif.gif)
- DM94 exclude convection at Rosseland mean
optical depths
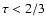 implicitly by the
specific
implicitly by the
specific 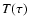 relation they use in
their photospheric model, see Chabrier &
Baraffe (1997) for a more detailed discussion.
relation they use in
their photospheric model, see Chabrier &
Baraffe (1997) for a more detailed discussion.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...1987)
![[*]](/icons/foot_motif.gif)
- The model described by Kuhfuß (1986) is very similar to
the 1987 version but the latter contains a more careful
discussion and treatment of the mixing-length limit of
the model.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
isopleths
![[*]](/icons/foot_motif.gif)
- From the greek words
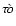
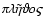 and
and
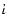
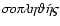 meaning "mass'' or "crowd'' and "being of the same mass'', respectively.
meaning "mass'' or "crowd'' and "being of the same mass'', respectively.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... 1995)
![[*]](/icons/foot_motif.gif)
- The advantages of using higher order advection
schemes in adaptive mesh radiation hydrodynamics have been demonstrated by
Winkler & Norman (1986). "Radiative'' protostellar collapse has been
calculated earlier by using second order advection methods in the
WH80s code. Those calculations did use a different grid equation
(Winkler & Norman 1986). The VIP code is the first radiation
hydrodynamics code that combines more accurate advection schemes with the
much clearer grid equation by Dorfi & Drury (1987). The VIP code is
in many aspects related to the titan code (Gehmeyr & Mihalas 1993),
that is the offspring of the Winkler WH80s code (see Mihalas 1998). All
those codes are based on implicit numerical methods using a self-adaptive
grid.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... magnitude
![[*]](/icons/foot_motif.gif)
- We can estimate the mean mass accretion rate for star formation from
such a cloud by
 ,
with
,
with
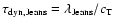 and obtain
and obtain
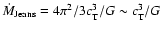 ,
which is a valid estimate as long as the mean cloud densities are close
to those of equilibrium configurations (singular or regular)
and the temperature, and as a
consequence the sound speed,
,
which is a valid estimate as long as the mean cloud densities are close
to those of equilibrium configurations (singular or regular)
and the temperature, and as a
consequence the sound speed, 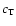 ,
does not change. For our cloud
assumptions we obtain
,
does not change. For our cloud
assumptions we obtain
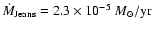 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... 1991a)
![[*]](/icons/foot_motif.gif)
- The optical depth scale height is equal to the pressure
scale height in classical, compact static photospheres
(Baschek et al. 1991), hence the
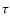 refinement translates into
a
refinement translates into
a 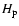 -refinement.
-refinement.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.