A&A 398, 1081-1090 (2003)
DOI: 10.1051/0004-6361:20021707
G. Wuchterl1,2 - W. M. Tscharnuter2,3
1 - Max-Planck-Institut für extraterrestrische Physik,
Giessenbachstraße, 85748 Garching, Germany
2 -
Institut für Theoretische Astrophysik der
Universität Heidelberg,
Tiergartenstraße 15, 69121 Heidelberg, Germany
3 -
Interdisziplinäres Zentrum für Wissenschaftliches
Rechnen der Universität Heidelberg,
Im Neuenheimer Feld 368, 69120 Heidelberg, Germany
Received 16 June 1999 / Accepted 8 November 2002
Abstract
We present the first study of early stellar evolution with
``cloud'' initial conditions utilizing a system of equations
that comprises a solar model solution.
All previous studies of protostellar collapse either make
numerous assumptions specifically tailored for different parts of the
flow and
different parts of the evolution or they do not reach the pre-main
sequence phase.
We calculate the pre-main sequence properties of marginally gravitationally
unstable, isothermal, equilibrium "Bonnor-Ebert'' spheres with an
initial temperature of
![]() and masses of 0.05 to 10
and masses of 0.05 to 10 ![]() .
The mass accretion rate is determined by the
solution of the flow equations rather than being prescribed or neglected.
In our study we determine the protostar's radii and the thermal structure
together with the mass and mass accretion rate, luminosity and effective
temperature during its evolution to a stellar pre-main sequence object.
We calculate the time needed to accrete the final stellar masses,
the corresponding mean mass accretion rates and median luminosities,
and the corresponding evolutionary tracks in the theoretical
Hertzsprung-Russell diagram.
We derive these quantities from the gas flow resulting from cloud collapse.
We do not assume a value for an "initial'' stellar radius and an "initial''
stellar thermal structure at the "top of the track'', the Hayashi-line or
any other instant of the evolution.
Instead we solve the flow equations for a cloud fragment with
spherical symmetry. The system of equations we use contains the equations
of stellar structure and evolution as a limiting case and has been tested
by a standard solar model and by classical stellar pulsations
(Wuchterl & Feuchtinger 1998;
Feuchtinger 1999;
Dorfi & Feuchtinger 1999).
When dynamical accretion effects have become sufficiently small so that
a comparison to existing hydrostatic stellar evolution calculations for
corresponding masses can be made, young stars of
.
The mass accretion rate is determined by the
solution of the flow equations rather than being prescribed or neglected.
In our study we determine the protostar's radii and the thermal structure
together with the mass and mass accretion rate, luminosity and effective
temperature during its evolution to a stellar pre-main sequence object.
We calculate the time needed to accrete the final stellar masses,
the corresponding mean mass accretion rates and median luminosities,
and the corresponding evolutionary tracks in the theoretical
Hertzsprung-Russell diagram.
We derive these quantities from the gas flow resulting from cloud collapse.
We do not assume a value for an "initial'' stellar radius and an "initial''
stellar thermal structure at the "top of the track'', the Hayashi-line or
any other instant of the evolution.
Instead we solve the flow equations for a cloud fragment with
spherical symmetry. The system of equations we use contains the equations
of stellar structure and evolution as a limiting case and has been tested
by a standard solar model and by classical stellar pulsations
(Wuchterl & Feuchtinger 1998;
Feuchtinger 1999;
Dorfi & Feuchtinger 1999).
When dynamical accretion effects have become sufficiently small so that
a comparison to existing hydrostatic stellar evolution calculations for
corresponding masses can be made, young stars of
![]() appear
close to the location of the Henyey part of the respective classical
evolutionary track and at substantially larger ages for given luminosities
than those inferred from previous calculations.
appear
close to the location of the Henyey part of the respective classical
evolutionary track and at substantially larger ages for given luminosities
than those inferred from previous calculations.
![]() stars
appear at lower luminosities, to the left of the corresponding
Hayashi-tracks
and are about
stars
appear at lower luminosities, to the left of the corresponding
Hayashi-tracks
and are about
![]() older than an a-priori hydrostatic stellar
evolution model at the same luminosity.
They burn most of their deuterium during the main accretion phase before
mass accretion halts and they become visible. They do not become
fully convective during the entire evolution calculated, i.e., up to 1.5 Myr. Altogether the structure of our solar mass star at 1 Myr, with its
raditive core and convective envelope, resembles the present Sun
rather then a fully convective object.
Very low mass stars and proto brown dwarfs close to the substellar limit
appear with luminosities close to those at the
"top of the tracks'', giving ages roughly in accordance with classical values,
tentatively at 0.05 to
older than an a-priori hydrostatic stellar
evolution model at the same luminosity.
They burn most of their deuterium during the main accretion phase before
mass accretion halts and they become visible. They do not become
fully convective during the entire evolution calculated, i.e., up to 1.5 Myr. Altogether the structure of our solar mass star at 1 Myr, with its
raditive core and convective envelope, resembles the present Sun
rather then a fully convective object.
Very low mass stars and proto brown dwarfs close to the substellar limit
appear with luminosities close to those at the
"top of the tracks'', giving ages roughly in accordance with classical values,
tentatively at 0.05 to
![]() higher effective temperatures.
higher effective temperatures.
Key words: stars: formation - stars: pre-main sequence - evolution - hydrodynamics - convection
One important aim of star formation theory, which is still an unsolved
problem, is to provide the initial conditions for stellar
evolution, i.e., the masses, radii and the internal structure of young
stars as soon as they can be considered to be in hydrostatic equilibrium
for the first time.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{M1_DM94_Col_3T.eps} \end{figure}](/articles/aa/full/2003/06/aa8963/Timg51.gif) |
Figure 1:
Early stellar evolution in the Hertzsprung-Russell diagram:
Comparison of results for the collapse of a
|
| Open with DEXTER | |
We account for all of the mentioned processes that are of importance in clouds and stars. However, we assume spherical symmetry and the grey Eddington approximation for radiative transfer to keep the problem as simple as possible, since this is the first look at the problem of cloud collapse, star formation and early stellar evolution that is based on the solution of one set of equations for all evolutionary stages. In the next section we assemble this system of equations that contains all the physics described above.
To discuss the results and illustrate the differences we focus on the comparison with classical, i.e., fully hydrostatic results that are obtained with model equations (stellar evolution equations) being as close as possible to the "stellar structure limit'' of our set of equations. Comparison of our results with studies that include more physical processes (e.g., disc accretion or frequency dependent photospheric radiative transfer) can then be made by using existing intercomparisons of different hydrostatic studies to our hydrostatic reference study.
To relate our results to quasi-hydrostatic stellar evolution
calculations on the pre-main sequence we chose the calculations by D'Antona &
Mazzitelli (1994), DM94, as our reference for the following reasons:
(1), the photospheric radiative transfer in DM94 is an
almost![]() accurate limit of our grey radiative transfer in the Eddington approximation
in its "stellar structure limit''. We thereby exclude differences between
our calculations and the quasi-hydrostatic calculations which might be due
to effects that are specific to the details of the non-grey treatment of
the photospheres.
(2), the low temperature, molecular opacities for DM94, "Alexander'' sets of
PMS-tracks are the same as used here.
(3), standard mixing length convection, our "stellar structure limit''
for convection, is one of the convection theories used by DM94.
accurate limit of our grey radiative transfer in the Eddington approximation
in its "stellar structure limit''. We thereby exclude differences between
our calculations and the quasi-hydrostatic calculations which might be due
to effects that are specific to the details of the non-grey treatment of
the photospheres.
(2), the low temperature, molecular opacities for DM94, "Alexander'' sets of
PMS-tracks are the same as used here.
(3), standard mixing length convection, our "stellar structure limit''
for convection, is one of the convection theories used by DM94.
We use the equations of radiation hydrodynamics (RHD) in the grey Eddington
approximation and with spherical symmetry (Castor 1972; Mihalas &
Mihalas 1984) in their integral form (Winkler & Norman 1986).
Convective energy transfer and mixing is included by using a new,
time-dependent convection model derived from the model of Kuhfuß
(1987)![]() . It closely approximates standard mixing length theory in
a local,
static limit and has been successfully tested in calculations of the Sun and
RR Lyrae pulsations (Wuchterl & Feuchtinger 1998; Feuchtinger 1999a,b). The convection model is
used with the standard parameters given in Wuchterl & Feuchtinger (1998).
The few cases where the mixing length parameter
. It closely approximates standard mixing length theory in
a local,
static limit and has been successfully tested in calculations of the Sun and
RR Lyrae pulsations (Wuchterl & Feuchtinger 1998; Feuchtinger 1999a,b). The convection model is
used with the standard parameters given in Wuchterl & Feuchtinger (1998).
The few cases where the mixing length parameter
![]() is changed
are explicitly emphasised. In all other cases the standard value
is changed
are explicitly emphasised. In all other cases the standard value
![]() is used, which results in a solar model that is in
accord with standard solar models and the Sun for our
"stellar structure limit''. The equations and boundary conditions are summarized in
Table .1, in the Appendix.
Detailed equations of state (Wuchterl 1989, 1990) and
opacities for a (proto) solar composition are used
(X = 0.77, Y = 0.213, Z = 0.017,
is used, which results in a solar model that is in
accord with standard solar models and the Sun for our
"stellar structure limit''. The equations and boundary conditions are summarized in
Table .1, in the Appendix.
Detailed equations of state (Wuchterl 1989, 1990) and
opacities for a (proto) solar composition are used
(X = 0.77, Y = 0.213, Z = 0.017,
![]() ).
The equations of state have been
compared to the MHD equations of state (Mihalas et al. 1988)
and agree to better than the table-interpolation errors (cf. Götz 1993).
Opacities include the contribution of dust particles with
"interstellar'' properties (Yorke 1979, 1980a), Alexander & Ferguson (1994)
values in the molecular range and Weiss et al. (1990) Los Alamos high
temperature opacities (compilation by Götz 1993). Convective mixing of
deuterium and deuterium burning (with reaction rates from Caughlan &
Fowler 1988) are included as outlined in the next section.
).
The equations of state have been
compared to the MHD equations of state (Mihalas et al. 1988)
and agree to better than the table-interpolation errors (cf. Götz 1993).
Opacities include the contribution of dust particles with
"interstellar'' properties (Yorke 1979, 1980a), Alexander & Ferguson (1994)
values in the molecular range and Weiss et al. (1990) Los Alamos high
temperature opacities (compilation by Götz 1993). Convective mixing of
deuterium and deuterium burning (with reaction rates from Caughlan &
Fowler 1988) are included as outlined in the next section.
During early stellar evolution the first nuclear reaction that
contributes significantly to the energy budget of a young star
is the D burning reaction
![]() (e.g.,
Kippenhahn & Weigert 1990). The energy
release of
(e.g.,
Kippenhahn & Weigert 1990). The energy
release of
![]() per reaction contributes as a source
per reaction contributes as a source
![]() to our internal energy equation
(cf. Table .1). The proton partial density,
to our internal energy equation
(cf. Table .1). The proton partial density,
![]() ,
is approximated by the
hydrogen partial density,
,
is approximated by the
hydrogen partial density,
![]() .
Once D becomes significantly depleted, it has to be budgeted by the
D balance equation that accounts for D destruction and transfer
from regions of different D abundance due to advection and
the D flux due to convective mixing,
.
Once D becomes significantly depleted, it has to be budgeted by the
D balance equation that accounts for D destruction and transfer
from regions of different D abundance due to advection and
the D flux due to convective mixing, ![]() ,
(see, Table .1, Eq. (3)).
Rate coefficients,
,
(see, Table .1, Eq. (3)).
Rate coefficients,
![]() for
for
![]() are
taken from Caughlan & Fowler (1988).
D burning via
are
taken from Caughlan & Fowler (1988).
D burning via
![]() is the only nuclear reaction
that we take into account. As a consequence, our study is limited to
evolutionary phases before the onset of hydrogen burning and does not
address the evolution of abundances of trace species like
is the only nuclear reaction
that we take into account. As a consequence, our study is limited to
evolutionary phases before the onset of hydrogen burning and does not
address the evolution of abundances of trace species like
![]() and
and ![]() .
.
It is assured that our extensions to the system of stellar structure equations do have a fixed relation to standard stellar structure and stellar hydrodynamics. After requiring a correct solar convection zone in the "stellar structure limit'', the equations we use do not contain any additional free parameters and the formation and evolution of a star is determined by the properties of the initial cloud fragment alone. The star formation theory is fully specified with the specification of the initial cloud state and the boundary conditions. See Appendix A for the equations.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{lgL_lgAge_MMLtrack.eps} \end{figure}](/articles/aa/full/2003/06/aa8963/Timg62.gif) |
Figure 2:
The relation between age and luminosity for the collapse of
Bonnor-Ebert spheres ( full lines) and classical, fully hydrostatic
models of pre-main sequence evolution. These relations are relevant for
the determination of PMS-ages. For the comparison we use the
quasi-hydrostatic results by D'Antona & Mazzitelli (1994)
("Alexander + MLT'' case) for
0.1, 0.5, 1 and
|
| Open with DEXTER | |
The results described below are quantities derived from the flows which are obtained as the solution of equations given in Table .1, for the Bonnor-Ebert collapses. Since there is no a priori hydrostatic part and no a priori photospheric model in our model (they result as special properties of the solutions of our flow equations) we describe how the stellar parameters age, effective temperature, radii and masses are obtained from the radiation hydrodynamical flows. We restrict our discussion mostly to these basic parameters to give an overview over the collapse solutions. We start our discussion with a proposal for the definition of zero stellar age, because as it turns out that most our definitions of stellar parameters will only be valid after this instant of time.
The modeling of the star formation process together with the
PMS-contraction opens up the possibility to define a stellar zero age.
We require the instant of age zero to be
(1), well defined,
(2), a unique clock for an individual star; it should be reset by
a destruction of the star and stellar mergers, and
(3), the gravitationally weakly bound, tenuous states of the cloud should
not contribute to stellar age - a long-lasting quasi-static cloud phase
would otherwise induce almost arbitrary age additions without any
consequences for the subsequent evolution.
To compare the luminosities of objects of various masses at a given age
a general definition of zero age is necessary. As the thermally
controlled Kelvin-Helmholtz contraction is the dominating evolutionary
process in young gas spheres, whether they are giant planets, brown dwarfs
or stars, we propose to use as age zero the instant of time, when the
interior of the gas spheres is thermally enclosed for the first time.
The enclosure means that photons
cannot escape from the entire object directly
but are radiated from a photosphere.
Energy transfer to the photospheric bottleneck then
delays the cooling and determines how the thermal reservoir in the
interior is emptied. The cooling history can then be used to define an
age since the heat reservoir was formed. As a practical
definition for age zero we propose to use the instant of time
when the Rosseland mean optical depth of a gaseous object equals 2/3, i.e.,
For a protostar this instant of time is practically at the end of the
isothermal phase of the collapse. Furthermore, with definition (1)
the luminosities of the protoplanets can be compared to stars and brown
dwarfs of similar age.
The proposed definition of zero age has the following properties:
(1), it preceeds the short phase of the "final hydrostatic
core formation'' for protostars that was used in earlier work
(Appenzeller & Tscharnuter 1975; Winkler & Newman 1980a)
by only ![]()
![]() .
It corresponds to the sharp
initial luminosity rise
(within 1000 yr for 0.05 to 10
.
It corresponds to the sharp
initial luminosity rise
(within 1000 yr for 0.05 to 10 ![]() )
that occurs
when the first (molecular hydrogen) protostellar cores form.
Because this happens during this rapid dynamical density enhancement
due to early cloud collapse, the proposed definition is very sharp,
in the sense that the properties
of the cloud vary rapidly in the vicinity of zero age;
)
that occurs
when the first (molecular hydrogen) protostellar cores form.
Because this happens during this rapid dynamical density enhancement
due to early cloud collapse, the proposed definition is very sharp,
in the sense that the properties
of the cloud vary rapidly in the vicinity of zero age;
![]() is reached during a phase of rapid changes in the observables. As a
consequence it will be observationally well defined;
(2), it is "close'' to the formation time of the oldest "rocks'' in the
solar system. They presumably form during the process of planetesimal
formation that occurs according to present understanding within
is reached during a phase of rapid changes in the observables. As a
consequence it will be observationally well defined;
(2), it is "close'' to the formation time of the oldest "rocks'' in the
solar system. They presumably form during the process of planetesimal
formation that occurs according to present understanding within
![]()
![]() after pre-planetary nebula formation. The pre-planetary
nebula forms roughly at the time when the final hydrostatic protostellar
core settles into hydrostatic equilibrium (Tscharnuter 1987).
Hence, together with the
after pre-planetary nebula formation. The pre-planetary
nebula forms roughly at the time when the final hydrostatic protostellar
core settles into hydrostatic equilibrium (Tscharnuter 1987).
Hence, together with the ![]()
![]() for final core formation,
the ages of the oldest meteorites and meteoritic components that
are determined by
absolute radioactive dating should be only
for final core formation,
the ages of the oldest meteorites and meteoritic components that
are determined by
absolute radioactive dating should be only ![]()
![]() smaller than the ages defined here. This results in a conceptual consistency
of our ages and the meteoritic ages to within probably <
smaller than the ages defined here. This results in a conceptual consistency
of our ages and the meteoritic ages to within probably <
![]() .
It is a useful property because solar system ages of
.
It is a useful property because solar system ages of
![]() Gyr
(Allègre et al. 1995; for Allende CAIs) are
used to calibrate stellar structure theory by assuming that the age of the
Sun is equal to the age of the meteorites and a comparison of
stellar-evolution models of the Sun at theoretical ages with properties
of the present Sun;
(3), relative ages of different objects in a star formation region
are physically well defined;
(4), the thermal clock which is based on the dominating dynamical process
in early stellar evolution, namely gravitational contraction and
cooling is (re)set at the proposed zero age;
(5), the age spread in young clusters is conceptually accessible without
reference to the ZAMS, and knowledge about it. Concepts involving the
ZAMS rely on the assumption that it will be reached. This is not
guaranteed as it does not exist for brown dwarfs and planets. Hence
such concepts would be inapplicable for those objects.
Our proposed zero age is a well defined concept for all masses at least
from an earth mass up to the largest stellar masses;
(6), questions about coevolution of very young binaries can be addressed
because individual component ages are well defined;
(7), with this zero age we use the earliest instant when an effective
temperature can be defined, based on a radius defined by using
optical depth.
With age definition (1) we can study the luminosity emitted by our
cloud volume as a function of age. In the beginning the luminosity comes
from the still almost isothermal cloud fragment, in the end from the
pre-main sequence star that has formed in the centre. We will use this
age to discuss the effect of the cloud collapse on pre-main sequence
ages. We can expect two main effects relative to hydrostatic models
of early stellar evolution: (i) an age offset that is due to
the fact that the collapse phase which is not modeled in fully hydrostatic
PMS-studies adds contributions of the order of a free-fall time
to the ages usually given (see Tables 1, 2),
and (ii) an effect due to the different PMS-contraction behaviour that
is due to the difference between the assumed initial thermal structure
of classical PMS-calculations and the thermal structure as calculated
from the collapse and accretion process in this work.
Gyr
(Allègre et al. 1995; for Allende CAIs) are
used to calibrate stellar structure theory by assuming that the age of the
Sun is equal to the age of the meteorites and a comparison of
stellar-evolution models of the Sun at theoretical ages with properties
of the present Sun;
(3), relative ages of different objects in a star formation region
are physically well defined;
(4), the thermal clock which is based on the dominating dynamical process
in early stellar evolution, namely gravitational contraction and
cooling is (re)set at the proposed zero age;
(5), the age spread in young clusters is conceptually accessible without
reference to the ZAMS, and knowledge about it. Concepts involving the
ZAMS rely on the assumption that it will be reached. This is not
guaranteed as it does not exist for brown dwarfs and planets. Hence
such concepts would be inapplicable for those objects.
Our proposed zero age is a well defined concept for all masses at least
from an earth mass up to the largest stellar masses;
(6), questions about coevolution of very young binaries can be addressed
because individual component ages are well defined;
(7), with this zero age we use the earliest instant when an effective
temperature can be defined, based on a radius defined by using
optical depth.
With age definition (1) we can study the luminosity emitted by our
cloud volume as a function of age. In the beginning the luminosity comes
from the still almost isothermal cloud fragment, in the end from the
pre-main sequence star that has formed in the centre. We will use this
age to discuss the effect of the cloud collapse on pre-main sequence
ages. We can expect two main effects relative to hydrostatic models
of early stellar evolution: (i) an age offset that is due to
the fact that the collapse phase which is not modeled in fully hydrostatic
PMS-studies adds contributions of the order of a free-fall time
to the ages usually given (see Tables 1, 2),
and (ii) an effect due to the different PMS-contraction behaviour that
is due to the difference between the assumed initial thermal structure
of classical PMS-calculations and the thermal structure as calculated
from the collapse and accretion process in this work.
In our discussion, we use the relation between luminosity and age
for two reasons: (1) because of the uncertainties (both theoretical
and observational)
in the determination of the effective temperature of objects in the vicinity
of the Hayashi-tracks, and (2) because these tracks are very steep in the
HRD during the early PMS evolution - the luminosity decreases at
almost constant effective temperature. These relations for the collapse
of Bonnor-Ebert spheres of 0.1, 0.5, 1 and
![]() are depicted
in
Fig. 2. The relations determined from collapse (full lines)
originate from zero luminosity, i.e., before the cloud fragment starts to radiate
significantly. The fully hydrostatic relations (dotted lines) begin at an
assumed initial age and at a luminosity that is the consequence of the assumed
(usually fully convective, or n=3/2 polytrope) initial thermal structure.
are depicted
in
Fig. 2. The relations determined from collapse (full lines)
originate from zero luminosity, i.e., before the cloud fragment starts to radiate
significantly. The fully hydrostatic relations (dotted lines) begin at an
assumed initial age and at a luminosity that is the consequence of the assumed
(usually fully convective, or n=3/2 polytrope) initial thermal structure.
Notice the age offset of about
![]() ,
about a free-fall time,
between the beginning of the classical and collapse curves in all cases.
This is due to the assumed initial ages of fully hydrostatic calculations.
Next we look at the possibility of attributing all the differences to an age
offset. This could be done by shifting the classical curves upward to
higher ages until the luminosities match the new curves. Such a procedure
could be considered successful if the rates of change in luminosity of
classical and collapse L(t)-relations match, too. This would be
indicated by the luminosity difference between corresponding old and
new relations of the same mass to be constant.
For the
,
about a free-fall time,
between the beginning of the classical and collapse curves in all cases.
This is due to the assumed initial ages of fully hydrostatic calculations.
Next we look at the possibility of attributing all the differences to an age
offset. This could be done by shifting the classical curves upward to
higher ages until the luminosities match the new curves. Such a procedure
could be considered successful if the rates of change in luminosity of
classical and collapse L(t)-relations match, too. This would be
indicated by the luminosity difference between corresponding old and
new relations of the same mass to be constant.
For the
![]() case this is fairly successful and the
collapse may be essentially viewed as producing an age offset of about
case this is fairly successful and the
collapse may be essentially viewed as producing an age offset of about
![]() .
For the other masses this procedure does not hold.
Even for the
.
For the other masses this procedure does not hold.
Even for the
![]() relations an addition of
relations an addition of
![]() to the classical relation might just bring the luminosities in accord, but
the relations still diverge because of the different contraction behaviour.
to the classical relation might just bring the luminosities in accord, but
the relations still diverge because of the different contraction behaviour.
The consequences for the inferred ages at given luminosity are already
considerable for
![]() :
at the end of the collapse
calculation, a PMS-object with solar luminosity has a new
age of
:
at the end of the collapse
calculation, a PMS-object with solar luminosity has a new
age of
![]() while following down the
while following down the
![]() -ordinate
to the classical tracks gives
-ordinate
to the classical tracks gives
![]() .
The situation is very similar
for
the 1 and
.
The situation is very similar
for
the 1 and
![]() clouds, but the differences in luminosity evolution to
the classical relations are even more pronounced. Changing the mixing length,
a procedure that probably produces the largest changes in classical models
does not significantly change this conclusion. This can be seen by comparing
the dashed and dash-dotted lines, for
clouds, but the differences in luminosity evolution to
the classical relations are even more pronounced. Changing the mixing length,
a procedure that probably produces the largest changes in classical models
does not significantly change this conclusion. This can be seen by comparing
the dashed and dash-dotted lines, for
![]() and 1.4, respectively,
that are very close to the standard 1
and 1.4, respectively,
that are very close to the standard 1 ![]() collapse relation for
collapse relation for
![]() .
.
Next the adopted age definition allows us to define the "stellar'' properties, i.e., the properties of the optically thick, ultimately hydrostatic parts of the flow for any instant after zero age. This is described in the next section.
Here we focus on the observables of the collapsing cloud fragments and the
resulting young stars, so we define our stellar radii to be the
optical depth radii, ![]() ,
obtained by determining the radius
r' at which
,
obtained by determining the radius
r' at which
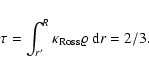 |
(2) |
The optical depth radius gives a measure of the radius
from which the photons escape and which parts of the flow are thermally
shielded from the outside. It is the length scale a (bolometric) observer
would see. It is very close to the density radius once the protostellar
cocoon has been sufficiently diluted by accretion to make it transparent
down to the stellar photosphere. The two radii converge when
![]() "jumps'' from the dust photosphere to the stellar photosphere
and intercepts
"jumps'' from the dust photosphere to the stellar photosphere
and intercepts ![]() .
.
With the luminosity at the outer boundary and the optical depth radius
we determine an effective temperature by
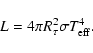 |
(3) |
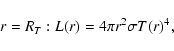 |
(4) |
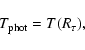 |
(5) |
In a static, compact, radiative photosphere in Eddington approximation, the definitions result in the same temperatures (cf. Baschek et al. 1991).
The resulting theoretical Hertzsprung-Russell diagram for the collapse of
a
![]() Bonnor-Ebert sphere is shown in Fig. 1.
In this case the mixing length parameter
Bonnor-Ebert sphere is shown in Fig. 1.
In this case the mixing length parameter
![]() is chosen to
be 1.4 to facilitate
the comparison with the fully hydrostatic pre-main sequence calculation.
The thick line shows the evolutionary track in the Hertzsprung-Russell diagram
by using the effective temperature based on the optical depth radius
is chosen to
be 1.4 to facilitate
the comparison with the fully hydrostatic pre-main sequence calculation.
The thick line shows the evolutionary track in the Hertzsprung-Russell diagram
by using the effective temperature based on the optical depth radius ![]() (as used in earlier collapse studies by Appenzeller & Tscharnuter 1975 and
Winkler & Newman 1980a). The track starts at the instant of zero age, indicated
by the diamond symbol. As above noted the adopted definition of zero age coincides
with the first instant at which the effective temperature concept can be used.
(as used in earlier collapse studies by Appenzeller & Tscharnuter 1975 and
Winkler & Newman 1980a). The track starts at the instant of zero age, indicated
by the diamond symbol. As above noted the adopted definition of zero age coincides
with the first instant at which the effective temperature concept can be used.
The initial decrease in
![]() is due to the fact that by definition
is due to the fact that by definition
![]() starts out very small but rapidly increases during the first core
formation. This occurs because the core's density and optical depth increase
rapidly during this settling into hydrostatic equilibrium.
starts out very small but rapidly increases during the first core
formation. This occurs because the core's density and optical depth increase
rapidly during this settling into hydrostatic equilibrium. ![]() increases
at approximately constant luminosity and hence
increases
at approximately constant luminosity and hence
![]() drops.
Temperatures given before zero age
(dash-dotted part) are central temperatures of the still transparent,
almost isothermal cloud. With the onset of accretion onto the
core the luminosity rises sharply with a moderate increase in
drops.
Temperatures given before zero age
(dash-dotted part) are central temperatures of the still transparent,
almost isothermal cloud. With the onset of accretion onto the
core the luminosity rises sharply with a moderate increase in
![]() .
The "mouse-head'' is the hall mark of the formation of the second (inner)
atomic hydrogen core that forms after the (second) collapse of the
dissociating molecular hydrogen core. At the cusp after the first luminosity
maximum the final accretion phase is entered. As the luminosity rises towards
the second maximum, the first core is accreted onto the second one and the
Mach numbers of the flow increase above ten. The small luminosity decrease
after the second maximum accompanies the adjustment of the accretion flow
and the mass accretion rate onto the final core to the substantial luminosity
now radiated from the accretion shock.
.
The "mouse-head'' is the hall mark of the formation of the second (inner)
atomic hydrogen core that forms after the (second) collapse of the
dissociating molecular hydrogen core. At the cusp after the first luminosity
maximum the final accretion phase is entered. As the luminosity rises towards
the second maximum, the first core is accreted onto the second one and the
Mach numbers of the flow increase above ten. The small luminosity decrease
after the second maximum accompanies the adjustment of the accretion flow
and the mass accretion rate onto the final core to the substantial luminosity
now radiated from the accretion shock.
When the luminosity starts rising
again the quasi-steady main-accretion phase commences. Shortly after the flat
top part of the track is reached, the luminosity, due to
D burning, becomes significant and reaches a maximum of 60% at the
global luminosity maximum.
When the volume is significantly depleted by the accretion process the
luminosity starts decreasing and
![]() rises as parts of the flow
closer to the young star become visible. When the dust cocoon becomes transparent
the optical depth radius "jumps'' into the "stellar'' photosphere the effective
temperature sharply increases, crosses the classical PMS-track, the
Hayashi line and finally reaches the "corner'' of the collapse track, at maximum
rises as parts of the flow
closer to the young star become visible. When the dust cocoon becomes transparent
the optical depth radius "jumps'' into the "stellar'' photosphere the effective
temperature sharply increases, crosses the classical PMS-track, the
Hayashi line and finally reaches the "corner'' of the collapse track, at maximum
![]() .
From this point on
.
From this point on
![]() coincides with the temperature
definition based on the temperature radius (thick and dashed line
overlap).
coincides with the temperature
definition based on the temperature radius (thick and dashed line
overlap).
Hence the radiation hydrodynamical results for temperature based on
RT and ![]() converge to the equality valid in classical, hydrostatic
photospheres. The photospheric
temperature (dotted) at
converge to the equality valid in classical, hydrostatic
photospheres. The photospheric
temperature (dotted) at ![]() passes the shock at this instant and
produces
a sharp spike to the left as
passes the shock at this instant and
produces
a sharp spike to the left as ![]() is at the peak temperature
just downstream from the accretion shock, and still upstream from
the radiative relaxation layer. As the
accretion luminosity becomes negligibly small and after "D burnout'' the collapse
track turns almost parallel to the classical track, slightly pointing towards
the ZAMS location of the Sun on the classical track. The photospheric
temperature remains different from the other two temperatures, and slightly
cooler than the
is at the peak temperature
just downstream from the accretion shock, and still upstream from
the radiative relaxation layer. As the
accretion luminosity becomes negligibly small and after "D burnout'' the collapse
track turns almost parallel to the classical track, slightly pointing towards
the ZAMS location of the Sun on the classical track. The photospheric
temperature remains different from the other two temperatures, and slightly
cooler than the
![]() value of the fully hydrostatic classical track.
Note that the photosphere of the collapse calculation is convective all along
the Hayashi-part of the track and
value of the fully hydrostatic classical track.
Note that the photosphere of the collapse calculation is convective all along
the Hayashi-part of the track and
![]() ,
valid for a compact,
hydrostatic, radiative photosphere in Eddington approximation
is not guaranteed under these conditions.
,
valid for a compact,
hydrostatic, radiative photosphere in Eddington approximation
is not guaranteed under these conditions.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{hrd_m_track_lglt_big.eps} \end{figure}](/articles/aa/full/2003/06/aa8963/Timg87.gif) |
Figure 3:
Evolutionary tracks in the Hertzsprung-Russell diagram for the
collapse and early pre-main sequence evolution of 0.05, 0.1, 0.5, 1, 2
and
|
| Open with DEXTER | |
In Fig. 3 an
overview over the collapse and PMS evolution of Bonnor-Ebert-sphere
cloud fragments with masses of 0.05, 0.1, 0.5, 1, 2 and
![]() is given. They are compared to classical, non accreting, fully hydrostatic
tracks for 0.1, 0.5, 1, and
is given. They are compared to classical, non accreting, fully hydrostatic
tracks for 0.1, 0.5, 1, and
![]() after D'Antona &
Mazzitelli (1994). For the comparison an electronic version of their
"Alexander, MLT''-tracks for
after D'Antona &
Mazzitelli (1994). For the comparison an electronic version of their
"Alexander, MLT''-tracks for
![]() was used.
was used.
The early evolution dominated by the initial cloud collapse is very similar
for all masses. At an age of 1000 yr the first hydrostatic cores form,
with an age spread of a few hundred years. All fragments enter the
main accretion phase at an age slightly above 8 kyr. All tracks remain
below effective temperatures of
![]() up to
up to
![]() .
The
protostars still remain in
their dust cocoons and radiate from dust photospheres.
The luminosity decline has already started at this
age for the lowest mass fragment. At
.
The
protostars still remain in
their dust cocoons and radiate from dust photospheres.
The luminosity decline has already started at this
age for the lowest mass fragment. At
![]() the first object has
arrived on the pre-main sequence, close to the Hayashi track.
It has formed from the lowest mass cloud fragment of
the first object has
arrived on the pre-main sequence, close to the Hayashi track.
It has formed from the lowest mass cloud fragment of
![]() and is a young brown dwarf.
The higher mass fragments follow until the
and is a young brown dwarf.
The higher mass fragments follow until the
![]() fragment
arrives
on its PMS-track at
fragment
arrives
on its PMS-track at
![]() .
The
.
The
![]() fragment is still
accreting at
fragment is still
accreting at
![]() ,
with a hydrostatic central stellar embryo of
,
with a hydrostatic central stellar embryo of
![]() .
.
Figure 3 illustrates that star formation is a gravitational heating event that increases temperature by about two orders of magnitude. Due to the negative, so-called gravothermal specific heat of common, thermally supported self-gravitating systems the heating slows down when energy losses slow-down because matter becomes opaque due to the cross-sections of atoms. Ultimately nuclear energy is added which acts as a long-term thermostatic effect.
The early PMS evolution of the collapsed cloud fragments shows a relation
to the classical tracks that changes with mass. The
![]() fragment arrives close to the radiative, Henyey part of the corresponding
classical track. The
fragment arrives close to the radiative, Henyey part of the corresponding
classical track. The
![]() and the
and the
![]() case
arrive on the PMS with a luminosity corresponding to about half way down
on the convective, Hayashi parts
of the classical tracks. The
case
arrive on the PMS with a luminosity corresponding to about half way down
on the convective, Hayashi parts
of the classical tracks. The
![]() fragment arrives with
a luminosity corresponding to the top of the classical track.
The
fragment arrives with
a luminosity corresponding to the top of the classical track.
The
![]() fragment (a proto brown dwarf) is shown to give an
indication of the further mass dependence of the relation to the
fragment (a proto brown dwarf) is shown to give an
indication of the further mass dependence of the relation to the
![]() classical track.
For the two lowest masses the age difference can be attributed to an offset
in zero age. Furthermore, D burning has not begun for the
classical track.
For the two lowest masses the age difference can be attributed to an offset
in zero age. Furthermore, D burning has not begun for the
![]() case-as might be expected so close to the brown dwarf limit.
It follows that, by using the appropriate initial thermal structure, this
mass probably will show a quasi-classical PMS evolution starting near
the top of a Hayashi track and a somewhat higher effective temperature,
but, as found in previous studies, with the slow-down of contraction due
to D burning.
case-as might be expected so close to the brown dwarf limit.
It follows that, by using the appropriate initial thermal structure, this
mass probably will show a quasi-classical PMS evolution starting near
the top of a Hayashi track and a somewhat higher effective temperature,
but, as found in previous studies, with the slow-down of contraction due
to D burning.
On the other hand the
results of the collapse calculations indicate substantial corrections
in PMS stellar properties
for masses of
![]() and higher. PMS objects of
these masses already are half-way
in the direction of the Henyey-track when they become visible.
and higher. PMS objects of
these masses already are half-way
in the direction of the Henyey-track when they become visible.
Due to our radiation hydrodynamical approach only the masses of the cloud fragments are prescribed. The stellar mass and the corresponding mass accretion rate are calculated from the flow. Hence, quantities like stellar mass and mass accretion rate are determined during the evolution of the flow.
For our discussion it is useful to use the optically thick mass, ![]() ,
for further considerations. It follows naturally by determining the
mass inside the optical depth radius,
,
for further considerations. It follows naturally by determining the
mass inside the optical depth radius, ![]() that we have already
used in the definition of
that we have already
used in the definition of
![]() .
This corresponds to the
hydrostatic mass, defined, e.g., via the density radius
(cf. Baschek et al. 1991)
for most of the time but has to be distinguished during the very early
accretion when calculating the accretion-luminosity from
.
This corresponds to the
hydrostatic mass, defined, e.g., via the density radius
(cf. Baschek et al. 1991)
for most of the time but has to be distinguished during the very early
accretion when calculating the accretion-luminosity from
![]() .
We use
.
We use ![]() for the remainder.
for the remainder.
In order to show the stellar properties as accretion proceeds we display
lines of constant optically thick mass, ![]() - which we may call
isopleths
- which we may call
isopleths![]() -
in the Hertzsprung-Russell diagram in Fig. 4. It is the actual
stellar mass that determines the stellar properties and not the fragment
mass that includes the entire circumstellar environment under
consideration. The
-
in the Hertzsprung-Russell diagram in Fig. 4. It is the actual
stellar mass that determines the stellar properties and not the fragment
mass that includes the entire circumstellar environment under
consideration. The
![]() fragment, for example, starts as
the other fragments with
fragment, for example, starts as
the other fragments with
![]() and produces the corresponding
luminosities and effective temperatures despite of its
and produces the corresponding
luminosities and effective temperatures despite of its
![]() protostellar envelope.
protostellar envelope.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{hrd_m_track_lgLT_meff_big.eps} \end{figure}](/articles/aa/full/2003/06/aa8963/Timg100.gif) |
Figure 4:
Optically thick mass, |
| Open with DEXTER | |
To facilitate statistical comparison with observations of star formation
and to have values for the factors of order unity in scaling arguments we
give some quantities averaged over the star formation time for each
fragment in Tables 1 and 2.
Ages at
![]() ,
,
![]() are given in units of
Myr and the initial free-fall time; mean mass-accretion rates
are given in units of
Myr and the initial free-fall time; mean mass-accretion rates
![]() are given in units of
are given in units of
![]() and
and
![]() ;
M0 is the fragment
mass. For the luminosities the median values <L> are given in solar units.
;
M0 is the fragment
mass. For the luminosities the median values <L> are given in solar units.
| Accretion time duration and averages | ||||||
| M0 |
|
<L> | Remark | |||
|
|
|
|
||||
| 1 | 0.55 | 3.23 |
|
0.30 | 13.1 | RC1M |
| 1 | 0.60 | 3.54 |
|
0.28 | 14.1 | RCML15 |
| 1 | 0.55 | 3.26 |
|
0.30 | 12.8 | RCML14
|
| 1 | 0.54 | 3.18 |
|
0.31 | 11.9 | RCML12
|
| 0.05 | 0.038 | 4.51 |
|
0.22 | 1.02 | RC005M |
| 0.1 | 0.074 | 4.34 |
|
0.23 | 2.21 | RC01M |
| 0.5 | 0.32 | 3.81 |
|
0.26 | 7.58 | RC05M |
| 1 | 0.55 | 3.23 |
|
0.30 | 13.0 | RC1M |
| 2 | 1.28 | 3.64 |
|
0.27 | 25.1 | RC2M |
| Accretion time and averages for different end of accretion | |||||
| and a
|
|||||
|
|
M0 |
|
Remark | ||
| 0.99 | 0.60 |
|
1 | 1 | RCML15 |
| 0.99 | 0.55 |
|
1 | 1 | RC1M |
| 0.999 | 0.82 |
|
1 | 1 | RC1M |
| 0.9999 | 1.08 |
|
1 | 1 | RC1M |
| 0.99999 | 1.29 |
|
1 | 1 | RC1M |
| 0.70 |
|
10 | 4.46 | RC10M | |
To indicate the effects due to the time-dependence of the accretion flow and,
in particular, due to the temporal variation of ![]() ,
we split the star formation
time into 4 phases, based on
,
we split the star formation
time into 4 phases, based on
![]() .
By this procedure we obtain
4 different populations corresponding to different stages of the accretion
process. For each of the 4 phases we give averaged quantities, for fragment
masses, M0, of
0.05, 0.1, 0.5, 1 and
.
By this procedure we obtain
4 different populations corresponding to different stages of the accretion
process. For each of the 4 phases we give averaged quantities, for fragment
masses, M0, of
0.05, 0.1, 0.5, 1 and
![]() ,
in
Table 3.
,
in
Table 3.
A study with spherical symmetry can certainly not address all aspects of the star formation process, as magnetic fields and angular momentum are ignored, but it has the advantage that the process can be studied by keeping close to basic physical principles-at least as close as stellar evolution theory, with the notorious problem of the convection model.
Based on the concept of "maximum deduction at minimum assumptions'', spherical symmetry provides a useful limiting and reference case. With the symmetry assumption we are able to keep a close and explicit relation to the fundamental conservation laws and other basic physical principles. The essential modeling assumption that goes into this work then is the ever present problem of the convection model. But we have tried not to add further ambiguity that is not already present in the modeling of stellar evolution. As a consequence of our convection model the system of equations we use represents the structure of the Sun correctly. The number of free parameters in any study of star formation cannot be made smaller than in ours unless a parameter-free description of convection becomes available.
The energetics of the star formation process can be addressed rather completely, most notably because all relevant energy transfer processes, i.e., radiation, convection, advection and conduction can be described accurately. Very likely star formation is most efficient with zero angular momentum and hence a lower limit for star formation time and upper limits for luminositites and accretion-rates are obtained.
| Averages for 4 accretion phases separated by
|
||||||||||||||||
| M0 | 0.05 |
0.1 |
0.5 |
1 |
2 |
|||||||||||
| <L> | <L> | <L> | <L> | <L> | ||||||||||||
|
|
||||||||||||||||
|
|
16 |
|
1.28 | 30 |
|
2.92 | 126 |
|
12.4 | 189 |
|
19.5 | 496 |
|
34.1 | |
| (0.8,0.9] | 6 |
|
1.19 | 11 |
|
2.63 | 52 |
|
8.21 | 85 |
|
15.3 | 200 |
|
27.3 | |
| (0.9,0.99] | 16 |
|
0.51 | 32 |
|
0.97 | 144 |
|
4.60 | 280 |
|
8.22 | 592 |
|
13.9 | |
| (0.99,0.999] | 15 |
|
0.21 | 28 |
|
0.33 | 139 |
|
3.03 | 264 |
|
4.69 | 554 |
|
8.42 | |
With our assumptions we can describe the pre-main sequence evolution as a consequence of the star formation process, more precisely as a result of the collapse of Bonnor-Ebert spheres. All "stellar'' masses appear at locations in the HRD that are different from the ones predicted by classical, fully hydrostatic calculations. In particular, they do not start at the top of a classical, initially fully convective track or at the birthline. Those differences cannot be attributed to differences in energy transfer treatment or differences in microphysics since we have constructed our model equations in a way that assures a "stellar structure'' limit, that is approached during pre-main sequence contraction and that coincides with the assumptions made in our classical fully hydrostatic reference-study.
The ages obtained with collapse models differ significantly, i.e., up to 1 Myr,
from the ages derived from classical calculations. This is only in part due
to the fact that the time needed for collapse and accretion are not accounted
for in classical PMS calculations. The primary reason is that the contraction
behaviour of the young stars resulting from the collapse differs from
the one obtained for the usually assumed fully convective, isentropic, or
polytropic initial structures. The fact that deuterium is almost completely
burnt during the main accretion phase, i.e., before the PMS is reached for
all "truly'' stellar masses calculated here (the
![]() case is the
exception) also contributes to the difference.
Hence calculations of early stellar evolution depend
on the star formation process. Initial conditions are not forgotten in general.
Another way to summarize this is that the star formation time, in our study
about 3-4 free-fall times in all cases, is not sufficiently different from the
Kelvin-Helmholtz time-scale of young objects to separate initial energy
deposition into the star during the accretion phase from energy losses that
control the contraction to the main sequence. As a consequence,
protostellar collapse determines the PMS evolution.
case is the
exception) also contributes to the difference.
Hence calculations of early stellar evolution depend
on the star formation process. Initial conditions are not forgotten in general.
Another way to summarize this is that the star formation time, in our study
about 3-4 free-fall times in all cases, is not sufficiently different from the
Kelvin-Helmholtz time-scale of young objects to separate initial energy
deposition into the star during the accretion phase from energy losses that
control the contraction to the main sequence. As a consequence,
protostellar collapse determines the PMS evolution.
This effect is enhanced by the off-centre ingnition of D burning and its interaction with the thermal structure. Unlike during most of stellar evolution it is not only controlled by the existing thermal structure but helps also to conserve the global thermal structure outside thermal equilibrium. This differs from the usual behaviour close to complete equilibrium, e.g., of main sequence stars, where nuclear reactions are adjusted to the thermal needs of the star and re-establish global thermal equilibrium.
Our study re-emphasises the fact that star formation is an intrinsically time
dependent process, with variations in all flow quantities. We have tried to
tentatively group the young population into four different evolutionary phases
based on the fraction of the residual circumstellar mass around them.
We gave characteristic quantities for those phases showing that mass
accretion rates vary significantly over the main accretion phase.
Accretion rates are typically a few
![]() yr in the earliest
phase, a few
yr in the earliest
phase, a few
![]() yr for the last 10% and
a few
yr for the last 10% and
a few
![]() yr for the accretion of the last percent
of the final mass. Those values are not too far from what is currently inferred
from observations (e.g., Brown & Chandler 1999). Also our star formation times
of 0.07 to
yr for the accretion of the last percent
of the final mass. Those values are not too far from what is currently inferred
from observations (e.g., Brown & Chandler 1999). Also our star formation times
of 0.07 to
![]() for 0.1 to
for 0.1 to
![]() are consistent
with estimates from a comparison of T Tauri star- and embedded source
counts (Kenyon et al. 1990). Our median luminosities between about 0.3 to 10
are consistent
with estimates from a comparison of T Tauri star- and embedded source
counts (Kenyon et al. 1990). Our median luminosities between about 0.3 to 10 ![]() ,
depending on accretion phases, for cloud fragment masses from
0.01 to
,
depending on accretion phases, for cloud fragment masses from
0.01 to
![]() ,
make it much harder to construct a
"Class I luminosity problem'' than with the assumed constant, canonical mass
accretion rate of
,
make it much harder to construct a
"Class I luminosity problem'' than with the assumed constant, canonical mass
accretion rate of
![]() ,
that is in conflict with observations
(Brown & Chandler 1999).
Let us finally summarize our main points:
(1) the star formation processes, i.e., the protostellar collapse translates
initial cloud conditions into initial stellar thermal structure,
(2) pre-main sequence evolution depends qualitatively and
quantitatively on the collapse flows;
(3) D burning ignites and mostly occurs
during the accretion phase for cloud fragments of 0.5, 1, 2, and
,
that is in conflict with observations
(Brown & Chandler 1999).
Let us finally summarize our main points:
(1) the star formation processes, i.e., the protostellar collapse translates
initial cloud conditions into initial stellar thermal structure,
(2) pre-main sequence evolution depends qualitatively and
quantitatively on the collapse flows;
(3) D burning ignites and mostly occurs
during the accretion phase for cloud fragments of 0.5, 1, 2, and
![]() ;
(4) we confirm that protostars and PMS objects
have an outer convective shell and a
central radiative zone;
(5) the radiative core lasts at least to a (new) age of
1.5 Myr for cloud fragments of 0.5, 1, and
;
(4) we confirm that protostars and PMS objects
have an outer convective shell and a
central radiative zone;
(5) the radiative core lasts at least to a (new) age of
1.5 Myr for cloud fragments of 0.5, 1, and
![]() and we expect off-centre ignition of
hydrogen burning;
(6) collapse pre-main sequence tracks are initially cooler
than classical tracks. Later they cross the Hayashi
line rapidly and start their quasi-classical decent along a mixed
radiative/convective contraction track. After the final stellar
photosphere becomes visible they appear to the left of the
Hayashi lines. Typically at 0.05 dex hotter effective
temperatures than the corresponding classical, fully
hydrostatic pre-main sequence model;
(7) already during the early pre-main sequence phase the solar
mass case is roughly homologous to the Sun with its
radiative core rather
than to a fully convective star on the Hayashi track;
(8) collapse ages below 2 Myr are up to a Myr older than classical
ages for the same luminosity.
and we expect off-centre ignition of
hydrogen burning;
(6) collapse pre-main sequence tracks are initially cooler
than classical tracks. Later they cross the Hayashi
line rapidly and start their quasi-classical decent along a mixed
radiative/convective contraction track. After the final stellar
photosphere becomes visible they appear to the left of the
Hayashi lines. Typically at 0.05 dex hotter effective
temperatures than the corresponding classical, fully
hydrostatic pre-main sequence model;
(7) already during the early pre-main sequence phase the solar
mass case is roughly homologous to the Sun with its
radiative core rather
than to a fully convective star on the Hayashi track;
(8) collapse ages below 2 Myr are up to a Myr older than classical
ages for the same luminosity.
Acknowledgements
This work was supported by the Fonds zur Förderung der wissenschaftlichen Forschung (FWF) under project numbers S7305-AST and S7307-AST and the Deutsche Forschungsgemeinschaft (DFG), SFB 359 (collaborative research center of the German national science foundation on "Reactive flows, diffusion and transport''). GW thanks M. Feuchtinger for the collaboration on the convection model and sharing the version of the VIP-code and the computational environment that he developed, and H. Herndl for providing a subroutine for the calculation of D reaction rates. We thank E. Dorfi for developing and sharing the original version of the VIP-code and providing substantial amounts of computational resources on his VAX-cluster in Vienna where the computations were perfomed, and for comments and discussion. We thank Christian Straka for reading the manuscript. We are indebted to Prof. H. Petersmannfrom the Seminar für Klassische Philologie, University of Heidelberg, for a most elucidated advice on the semantics and etymology of the term isopleths.
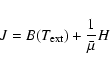 |
(A.1) |
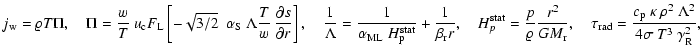 |
(A.9) | ||
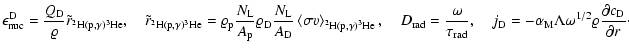 |
(A.10) |
that is, radiation
is streaming freely into an external reservoir emitting blackbody
radiation of
![]() .
All other surface terms vanish both at the outer cloud boundary
(e.g., no convective flux leaves the fragment) and at the centre, where
the interior mass
.
All other surface terms vanish both at the outer cloud boundary
(e.g., no convective flux leaves the fragment) and at the centre, where
the interior mass ![]() is zero. The total volume of the computed
domain is assumed to be constant, equal to the volume of the critical
Bonnor-Ebert sphere.
is zero. The total volume of the computed
domain is assumed to be constant, equal to the volume of the critical
Bonnor-Ebert sphere.
The equations are solved with a "protostellar'' version of the VIP-code
(Dorfi & Feuchtinger 1995), where convection is added as outlined by
Wuchterl (1995a). The equations are discretized following the principles
described by Winkler & Norman (1986) and Tscharnuter (1987, 1989) with
a tensor pseudo viscosity (Tscharnuter & Winkler 1979) and a
self-adaptive grid determined by an equation of the Dorfi & Drury (1987)
class. For a recent comparative discussion of discretisation techniques
see LeVeque (1998) and for an overview over the self-adaptive grid
method see Tscharnuter (1991) and Dorfi (1998).
The VIP code contains improvements with respect to other self-adaptive
grid codes used to calculate the protostellar collapse. The most important
one being a higher order (van Leer) advection scheme (see Dorfi &
Feuchtinger 1995)![]() .
The key advantage in the present context is that a higher order advection
scheme allows the grid to move faster, for a given advection error. Hence
grid points can be concentrated more rapidly and higher spatial resolution
can be obtained faster. The advection errors caused by local grid refinement
are an important "side effect'' of using an adaptive grid when very
high resolution is obtained on timescales that are much smaller than the
physical timescales in other parts of the flow (Kürschner 1994). This side
effect is only present when the flow is non steady and, as a consequence,
the motion of the gridpoints contributes to the advection errors.
.
The key advantage in the present context is that a higher order advection
scheme allows the grid to move faster, for a given advection error. Hence
grid points can be concentrated more rapidly and higher spatial resolution
can be obtained faster. The advection errors caused by local grid refinement
are an important "side effect'' of using an adaptive grid when very
high resolution is obtained on timescales that are much smaller than the
physical timescales in other parts of the flow (Kürschner 1994). This side
effect is only present when the flow is non steady and, as a consequence,
the motion of the gridpoints contributes to the advection errors.
For our calculations of the protostellar collapse, modifications of the VIP-code have been made. They can be understood as a consequence of the quantitative resolution requirements and accuracy demands of a protostellar collapse calculation. Many of these requirements have been discussed previously (Tscharnuter & Winkler 1979; Tscharnuter 1987; Morfill et al. 1985; Balluch 1991a-c; Kürschner 1994). We will briefly describe the modifications as motivated by a view based on the properties of self-gravitating equilibrium gas spheres (with radiation) as they are imposed onto those systems by their gravity. This emphasises the accuracy requirements that become increasingly important toward the end of the star formation process. Increasing fractions of the cloud fragment mass actually settle into hydrostatic equilibrium as the pre-main sequence is approached. Earlier high resolution studies focused on the accurate representation of the flow discontinuities (e.g., Balluch 1991a-c) because the hydrostatic parts were relatively easy to resolve with a self-adaptive grid. Nevertheless, they deserve a careful consideration because they contain a large fraction of the total mass. After all, that fraction should approach unity at the end of a star formation calculation.
At the end of a star formation calculation gravity becomes much more
important for the overall structure, especially in the outermost layers
of the stars, where temperature and pressures are smallest. After all,
the dominating effect of gravity is the key reason of why spherical symmetry
is a good approximation through most parts of stellar evolution.
For the Sun we obtain a ratio of the photospheric pressure scale height
to the solar radius, of
![]() .
.
For a star formation calculation this means that, as the cloud collapses,
gravity is becoming more and more dominating and the scale heights
are becoming correspondingly smaller.
In general the respective dimensionless number to specify the relative
length scale over which flow variables vary in a gravitating system
close to hydrostatic equilibrium is given by the compactness,
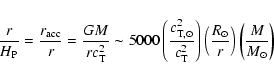 |
(B.1) |
When hydrostatic parts and a circumstellar gas flow are calculated
together, as is the case in our study, the compactness
directly translates into a lower limit for the required
local radial resolution (Wuchterl 1995a):
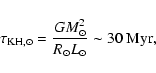 |
(B.3) |
A hydrodynamic calculation that does not satisfy the
resolution requirement (.2) cannot distinguish between a
dynamic pressure gradient caused, e.g., by a sound wave and the hydrostatic
"background'' structure! In practice there is, of course, much more
flow structure to be resolved on a pressure scale height. Radiative
transfer, e.g., requires a resolution in optical depth that sometimes
is much more stringent as it requires
![]() (cf. Balluch
1991a)
(cf. Balluch
1991a)![]() . The condition (.2) above and the resulting Courant
numbers therefore must be viewed as a demanding but still relatively weak
lower limit. In practice resolutions of
. The condition (.2) above and the resulting Courant
numbers therefore must be viewed as a demanding but still relatively weak
lower limit. In practice resolutions of
![]() are
needed towards the end of the calculations presented here.
are
needed towards the end of the calculations presented here.
The compactness is a dimensionless number that can be used
to quantify both the effects of gravity and the respective resolution
requirements in astrophysical radiation hydrodynamics. It can also
be used to distinguish between systems with different importance of
gravity effects (Wuchterl
1995a). The analogy to the square of the Mach number describing the
importance of inertial effects is displayed below:
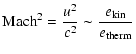 |
(B.4) |
For a calculation of protostellar collapse the condition (.2) means that, from the
equilibrium structure of gravitating systems alone, we have to resolve
at least structures starting from 0.1 to 10-4 of the local
radius. The latter is about 10-10 of the extension of the computational
domain, the initial volume of the cloud fragment.
In practice this is needed to describe the "background'' structure on
top of which the radiation hydrodynamics of the collapse proceeds.
In principle, the required resolutions are no problem for a self-adaptive
grid method and we could solve the Navier-Stokes equations with the
"molecular'' viscosity and omitting any pseudo viscosity as
demonstrated by Balluch (1991c). But this pushes present computer
floating point operations to its limits (quadruple precision is then
needed and slows down the computations considerably), and the
"realistic'' molecular viscosity might cause large advection errors during
time-dependent flow phases. To meet the resolution
requirements of gravitating equilibrium systems while keeping the
advection errors as small as possible we use a pseudo viscosity length
scale,
![]() ,
defined by
,
defined by
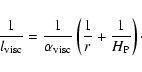 |
(B.5) |
The previous considerations guarantee that the spatial resolution
is sufficiently high but low enough to avoid unnecessary advection errors
when high resolution is required fast. In other words, grid induced advection
is avoided by considering the sources for grid motion during time-dependent
evolutionary phases. We also improved the advection scheme by demanding
volume conservation, i.e.,
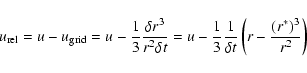 |
(B.7) |
![\begin{displaymath}\tau_{\rm grid} = g_\tau \left[ t_{\rm ff}\left(\frac{M}{4\pi r^3}\right)
+ 1000 \right] [\rm s] ,
\end{displaymath}](/articles/aa/full/2003/06/aa8963/img218.gif) |
(B.8) |
Secondly, to enhance the resolution in hydrostatic parts of the flow that
carry large fractions of the total energy (and total energy errors,
cf. Kürschner 1994) we weight the arc-length in our desired resolution
function (sometimes also called the monitor function) for the grid
equation motivated by a scaled estimate for the total potential energy content
of the respective mass shell,
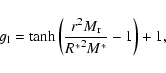 |
(B.9) |
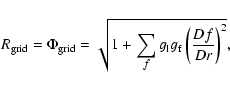 |
(B.10) |
Our general method to distinguish between different candidate prescriptions for the "arbitrary'' or "personally biased'' part of the Dorfi & Drury (1987) grid equation was to use the total energy conservation properties as a criterion. A better grid is considered to be one that conserves total energy better. By this approach the freedom in specifying the desired resolution function has been somewhat reduced compared to other studies.
The discretisation of the nuclear energy generation source
term to the internal energy equation is done analogously to other source
terms. The D balance equation is discretized in analogy to the continuity
equation. We note that we use D concentration as our additional
computational variable and that we use a discretization for ![]() which
is symmetric in the grid index.
which
is symmetric in the grid index.
The critical, i.e., marginally gravitationally unstable Bonnor-Ebert sphere
was determined numerically in the following way: We started with a homogeneous,
isothermal sphere of one tenth of the Jeans-critical density. After
dynamical relaxation this sphere becomes hydrostatic and quasi-homogeneous
with only a weak central density enhancement. The calculations are carried
out for a
given volume (originally, the volume corresponding to 0.1 of the Jeans
density) that is slowly contracted (at
![]() ).
The subcritical hydrostatic sphere therefore shrinks on the time-scale
).
The subcritical hydrostatic sphere therefore shrinks on the time-scale
![]() ,
which is
,
which is ![]()
![]() .
The calculations
(with the fully dynamic equations) proceed on this time-scale through a
sequence of essentially static isothermal spheres,
.
The calculations
(with the fully dynamic equations) proceed on this time-scale through a
sequence of essentially static isothermal spheres,
![]() until the marginally stable
equilibrium sphere is
reached and collapse sets in. This procedure guarantees that the initial
cloud condition is accurately static and that the critical state for
the detailed constitutive relations (most prominently the pressure equation of
state) is determined precisely.
until the marginally stable
equilibrium sphere is
reached and collapse sets in. This procedure guarantees that the initial
cloud condition is accurately static and that the critical state for
the detailed constitutive relations (most prominently the pressure equation of
state) is determined precisely.