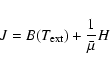 |
(A.1) |
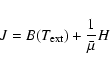 |
(A.1) |
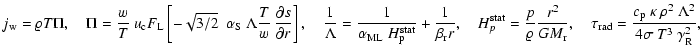 |
(A.9) | ||
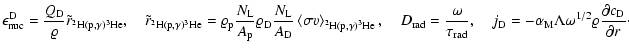 |
(A.10) |
that is, radiation
is streaming freely into an external reservoir emitting blackbody
radiation of
![]() .
All other surface terms vanish both at the outer cloud boundary
(e.g., no convective flux leaves the fragment) and at the centre, where
the interior mass
.
All other surface terms vanish both at the outer cloud boundary
(e.g., no convective flux leaves the fragment) and at the centre, where
the interior mass ![]() is zero. The total volume of the computed
domain is assumed to be constant, equal to the volume of the critical
Bonnor-Ebert sphere.
is zero. The total volume of the computed
domain is assumed to be constant, equal to the volume of the critical
Bonnor-Ebert sphere.
The equations are solved with a "protostellar'' version of the VIP-code
(Dorfi & Feuchtinger 1995), where convection is added as outlined by
Wuchterl (1995a). The equations are discretized following the principles
described by Winkler & Norman (1986) and Tscharnuter (1987, 1989) with
a tensor pseudo viscosity (Tscharnuter & Winkler 1979) and a
self-adaptive grid determined by an equation of the Dorfi & Drury (1987)
class. For a recent comparative discussion of discretisation techniques
see LeVeque (1998) and for an overview over the self-adaptive grid
method see Tscharnuter (1991) and Dorfi (1998).
The VIP code contains improvements with respect to other self-adaptive
grid codes used to calculate the protostellar collapse. The most important
one being a higher order (van Leer) advection scheme (see Dorfi &
Feuchtinger 1995)![]() .
The key advantage in the present context is that a higher order advection
scheme allows the grid to move faster, for a given advection error. Hence
grid points can be concentrated more rapidly and higher spatial resolution
can be obtained faster. The advection errors caused by local grid refinement
are an important "side effect'' of using an adaptive grid when very
high resolution is obtained on timescales that are much smaller than the
physical timescales in other parts of the flow (Kürschner 1994). This side
effect is only present when the flow is non steady and, as a consequence,
the motion of the gridpoints contributes to the advection errors.
.
The key advantage in the present context is that a higher order advection
scheme allows the grid to move faster, for a given advection error. Hence
grid points can be concentrated more rapidly and higher spatial resolution
can be obtained faster. The advection errors caused by local grid refinement
are an important "side effect'' of using an adaptive grid when very
high resolution is obtained on timescales that are much smaller than the
physical timescales in other parts of the flow (Kürschner 1994). This side
effect is only present when the flow is non steady and, as a consequence,
the motion of the gridpoints contributes to the advection errors.
For our calculations of the protostellar collapse, modifications of the VIP-code have been made. They can be understood as a consequence of the quantitative resolution requirements and accuracy demands of a protostellar collapse calculation. Many of these requirements have been discussed previously (Tscharnuter & Winkler 1979; Tscharnuter 1987; Morfill et al. 1985; Balluch 1991a-c; Kürschner 1994). We will briefly describe the modifications as motivated by a view based on the properties of self-gravitating equilibrium gas spheres (with radiation) as they are imposed onto those systems by their gravity. This emphasises the accuracy requirements that become increasingly important toward the end of the star formation process. Increasing fractions of the cloud fragment mass actually settle into hydrostatic equilibrium as the pre-main sequence is approached. Earlier high resolution studies focused on the accurate representation of the flow discontinuities (e.g., Balluch 1991a-c) because the hydrostatic parts were relatively easy to resolve with a self-adaptive grid. Nevertheless, they deserve a careful consideration because they contain a large fraction of the total mass. After all, that fraction should approach unity at the end of a star formation calculation.
At the end of a star formation calculation gravity becomes much more
important for the overall structure, especially in the outermost layers
of the stars, where temperature and pressures are smallest. After all,
the dominating effect of gravity is the key reason of why spherical symmetry
is a good approximation through most parts of stellar evolution.
For the Sun we obtain a ratio of the photospheric pressure scale height
to the solar radius, of
![]() .
.
For a star formation calculation this means that, as the cloud collapses,
gravity is becoming more and more dominating and the scale heights
are becoming correspondingly smaller.
In general the respective dimensionless number to specify the relative
length scale over which flow variables vary in a gravitating system
close to hydrostatic equilibrium is given by the compactness,
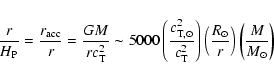 |
(B.1) |
When hydrostatic parts and a circumstellar gas flow are calculated
together, as is the case in our study, the compactness
directly translates into a lower limit for the required
local radial resolution (Wuchterl 1995a):
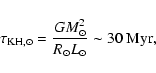 |
(B.3) |
A hydrodynamic calculation that does not satisfy the
resolution requirement (.2) cannot distinguish between a
dynamic pressure gradient caused, e.g., by a sound wave and the hydrostatic
"background'' structure! In practice there is, of course, much more
flow structure to be resolved on a pressure scale height. Radiative
transfer, e.g., requires a resolution in optical depth that sometimes
is much more stringent as it requires
![]() (cf. Balluch
1991a)
(cf. Balluch
1991a)![]() . The condition (.2) above and the resulting Courant
numbers therefore must be viewed as a demanding but still relatively weak
lower limit. In practice resolutions of
. The condition (.2) above and the resulting Courant
numbers therefore must be viewed as a demanding but still relatively weak
lower limit. In practice resolutions of
![]() are
needed towards the end of the calculations presented here.
are
needed towards the end of the calculations presented here.
The compactness is a dimensionless number that can be used
to quantify both the effects of gravity and the respective resolution
requirements in astrophysical radiation hydrodynamics. It can also
be used to distinguish between systems with different importance of
gravity effects (Wuchterl
1995a). The analogy to the square of the Mach number describing the
importance of inertial effects is displayed below:
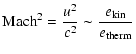 |
(B.4) |
For a calculation of protostellar collapse the condition (.2) means that, from the
equilibrium structure of gravitating systems alone, we have to resolve
at least structures starting from 0.1 to 10-4 of the local
radius. The latter is about 10-10 of the extension of the computational
domain, the initial volume of the cloud fragment.
In practice this is needed to describe the "background'' structure on
top of which the radiation hydrodynamics of the collapse proceeds.
In principle, the required resolutions are no problem for a self-adaptive
grid method and we could solve the Navier-Stokes equations with the
"molecular'' viscosity and omitting any pseudo viscosity as
demonstrated by Balluch (1991c). But this pushes present computer
floating point operations to its limits (quadruple precision is then
needed and slows down the computations considerably), and the
"realistic'' molecular viscosity might cause large advection errors during
time-dependent flow phases. To meet the resolution
requirements of gravitating equilibrium systems while keeping the
advection errors as small as possible we use a pseudo viscosity length
scale,
![]() ,
defined by
,
defined by
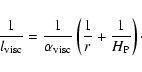 |
(B.5) |
The previous considerations guarantee that the spatial resolution
is sufficiently high but low enough to avoid unnecessary advection errors
when high resolution is required fast. In other words, grid induced advection
is avoided by considering the sources for grid motion during time-dependent
evolutionary phases. We also improved the advection scheme by demanding
volume conservation, i.e.,
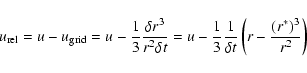 |
(B.7) |
![\begin{displaymath}\tau_{\rm grid} = g_\tau \left[ t_{\rm ff}\left(\frac{M}{4\pi r^3}\right)
+ 1000 \right] [\rm s] ,
\end{displaymath}](/articles/aa/full/2003/06/aa8963/img218.gif) |
(B.8) |
Secondly, to enhance the resolution in hydrostatic parts of the flow that
carry large fractions of the total energy (and total energy errors,
cf. Kürschner 1994) we weight the arc-length in our desired resolution
function (sometimes also called the monitor function) for the grid
equation motivated by a scaled estimate for the total potential energy content
of the respective mass shell,
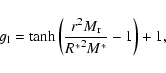 |
(B.9) |
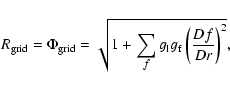 |
(B.10) |
Our general method to distinguish between different candidate prescriptions for the "arbitrary'' or "personally biased'' part of the Dorfi & Drury (1987) grid equation was to use the total energy conservation properties as a criterion. A better grid is considered to be one that conserves total energy better. By this approach the freedom in specifying the desired resolution function has been somewhat reduced compared to other studies.
The discretisation of the nuclear energy generation source
term to the internal energy equation is done analogously to other source
terms. The D balance equation is discretized in analogy to the continuity
equation. We note that we use D concentration as our additional
computational variable and that we use a discretization for ![]() which
is symmetric in the grid index.
which
is symmetric in the grid index.
The critical, i.e., marginally gravitationally unstable Bonnor-Ebert sphere
was determined numerically in the following way: We started with a homogeneous,
isothermal sphere of one tenth of the Jeans-critical density. After
dynamical relaxation this sphere becomes hydrostatic and quasi-homogeneous
with only a weak central density enhancement. The calculations are carried
out for a
given volume (originally, the volume corresponding to 0.1 of the Jeans
density) that is slowly contracted (at
![]() ).
The subcritical hydrostatic sphere therefore shrinks on the time-scale
).
The subcritical hydrostatic sphere therefore shrinks on the time-scale
![]() ,
which is
,
which is ![]()
![]() .
The calculations
(with the fully dynamic equations) proceed on this time-scale through a
sequence of essentially static isothermal spheres,
.
The calculations
(with the fully dynamic equations) proceed on this time-scale through a
sequence of essentially static isothermal spheres,
![]() until the marginally stable
equilibrium sphere is
reached and collapse sets in. This procedure guarantees that the initial
cloud condition is accurately static and that the critical state for
the detailed constitutive relations (most prominently the pressure equation of
state) is determined precisely.
until the marginally stable
equilibrium sphere is
reached and collapse sets in. This procedure guarantees that the initial
cloud condition is accurately static and that the critical state for
the detailed constitutive relations (most prominently the pressure equation of
state) is determined precisely.
Copyright ESO 2003