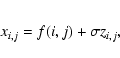
We now apply our digital transforms for removing noise from image data. The methodology is standard and is outlined mainly for the sake of clarity and self-containedness.
Suppose that one is given noisy data of the form
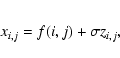
Let ![]() be the noisy curvelet coefficients
(y = F x). We use the following hard-thresholding rule
for estimating the unknown curvelet coefficients:
be the noisy curvelet coefficients
(y = F x). We use the following hard-thresholding rule
for estimating the unknown curvelet coefficients:
| (6) | |||
| (7) |
Assume now that we have Poisson data xi,j with unknown mean
f(i,j). The Anscombe transformation (Anscombe 1948)
For small number of counts, a possibility is to compute the Radon transform of the image, and then to apply the Anscombe transformation to the Radon data. The rationale being that, roughly speaking, the Radon transform corresponds to a summation of pixel values over lines and that the sum of independent Poisson random variables is a Poisson random variable with intensity equal to the sum of the individual intensities. Hence, the intensity of the sum may be quite large (hence validating the Gaussian approximation) even though the individual intensities may be small. This might be viewed as an interesting feature as unlike wavelet transforms, the ridgelet and curvelet transforms tend to average data over elongated and rather large neighborhoods.
The arrival of photons, and their expression by electron counts, on CCD
detectors may be modeled by a Poisson distribution. In addition, there is
additive Gaussian read-out noise.
The Anscombe
transformation (Eq. (8)) has been extended
to take this combined noise into account.
As an approximation, consider the signal's value, sk, as a sum of a Gaussian
variable, ![]() ,
of mean g and standard-deviation
,
of mean g and standard-deviation ![]() ;
and a
Poisson variable, n, of mean m0: we set
;
and a
Poisson variable, n, of mean m0: we set
![]() where
where ![]() is the gain.
The generalization of the variance stabilizing Anscombe formula is (Murtagh et al. 1995):
is the gain.
The generalization of the variance stabilizing Anscombe formula is (Murtagh et al. 1995):
Then, for an image containing Poisson and Poisson+Gaussian noise, we apply first respectively the Anscombe and the Generalized Anscombe transform.
These variance stabilization transformations, it has been shown in Murtagh et al. (1995), are only valid for a sufficiently large number of counts (and of course, for a larger still number of counts, the Poisson distribution becomes Gaussian). The necessary average number of counts is about 20 if bias is to be avoided. Note that errors related to small values carry the risk of removing real objects, but not of amplifying noise. For Poisson parameter values under this threshold acceptable number of counts, the Anscombe transformation loses control over the bias. In this case, an alternative approach to variance stabilization is needed. It has been shown that the first step of the ridgelet transform consists in a Radon transform. As a Radon coefficient is an addition of pixel values along a line, the Radon transform of an image containing Poisson noise contains also Poisson noise. Then the Anscombe transform can be applied after the Radon transformation rather than on the original image. The advantage is that the number of counts per pixel will obviously be larger in the Radon domain than in the image domain, and the variance stabilization will be more robust.
A Gaussian white noise with a standard deviation fixed to 20 was added to the Saturn image. We employed several methods to filter the noisy image:
Further results are visible at the following URL: http://www-stat.stanford.edu/~jstarck.
Figure 7 shows an example of an X-ray image filtering by the ridgelet transform using such an approach. Figure 7 left and right shows respectively the XMM/Newton image of the Kepler SN1604 supernova and the ridgelet filtered image (using a five sigma hard thresholding).
We have introduced in this paper two new transforms, the ridgelet transform and the curvelet transform. Several other transforms are often used in astronomy, such the Fourier transform, the isotropic à trous wavelet transform and the bi-orthogonal wavelet transform. The choise of the best transform may be delicate. Each transform has its own domain of optimality:
Copyright ESO 2003