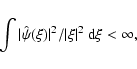2 The curvelet transform

2.1 The ridgelet transform

The two-dimensional continuous ridgelet transform in ${\vec R}^2$ can be defined as follows (Candès 1999). We pick a smooth univariate function $\psi$: ${\vec R} \rightarrow{\vec R}$ with sufficient decay and satisfying the admissibility condition

$$% \int \vert\hat{\psi}(\xi)\vert^2/\vert\xi\vert^2 ~ {\rm d}\xi < \infty,$$ (1)

which holds if, say, $\psi$ has a vanishing mean $\int \psi(t) {\rm d}t = 0$. We will suppose a special normalization about $\psi$ so that  $\int_0^\infty \vert\hat{\psi}(\xi)\vert^2 \xi^{-2} {\rm d}\xi = 1$.

For each a > 0, each $b \in {\vec R}$ and each $\theta \in [0,2\pi)$, we define the bivariate ridgelet $\psi_{a,b,\theta}$: ${\vec R}^2 \rightarrow {\vec R}$ by

$$% \psi_{a,b,\theta} (x) = a^{-1/2} \cdot \psi( (x_1 \cos\theta + x_2 \sin\theta - b)/a);$$ (2)

A ridgelet is constant along lines $x_1 \cos\theta + x_2 \sin\theta = {\rm const}$. Transverse to these ridges it is a wavelet.

Figure 2 graphs a few ridgelets with different parameter values. The top right, bottom left and right panels are obtained after simple geometric manipulations of the upper left ridgelet, namely rotation, rescaling, and shifting.

Given an integrable bivariate function f(x), we define its ridgelet coefficients by

$$\begin{eqnarray*}{\cal R}_f(a,b,\theta) = \int \overline{\psi}_{a,b,\theta}(x) f(x) {\rm d}x. \end{eqnarray*}$$

We have the exact reconstruction formula

$$% f(x) = \int_0^{2\pi} \int_{-\infty}^\infty \int_0^\infty {\... ...(x) ~\frac{{\rm d}a}{a^3} {\rm d}b~ \frac{{\rm d}\theta}{4\pi}$$ (3)

valid a.e. for functions which are both integrable and square integrable.

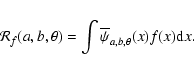
Ridgelet analysis may be constructed as wavelet analysis in the Radon domain. Recall that the Radon transform of an object f is the collection of line integrals indexed by  $(\theta,t) \in [0,2\pi) \times {\vec R}$ given by

$$% Rf(\theta,t) = \int f(x_1,x_2) \delta(x_1 \cos\theta + x_2 \sin\theta - t)~ {\rm d}x_1 {\rm d}x_2,$$ (4)

where $\delta$ is the Dirac distribution. Then the ridgelet transform is precisely the application of a 1-dimensional wavelet transform to the slices of the Radon transform where the angular variable $\theta$is constant and t is varying.

This viewpoint strongly suggests developing approximate Radon transforms for digital data. This subject has received a considerable attention over the last decades as the Radon transform naturally appears as a fundamental tool in many fields of scientific investigation. Our implementation follows a widely used approach in the literature of medical imaging and is based on discrete fast Fourier transforms. The key component is to obtain approximate digital samples from the Fourier transform on a polar grid, i.e. along lines going through the origin in the frequency plane.

2.2 An approximate digital ridgelet transform

2.2.1 Radon tranform

A fast implementation of the RT can be performed in the Fourier domain. First the 2D FFT is computed. Then it is interpolated along a number of straight lines equal to the selected number of projections, each line passing through the origin of the 2D frequency space, with a slope equal to the projection angle, and a number of interpolation points equal to the number of rays per projection. The one dimensional inverse Fourier transform of each interpolated array is then evaluated. The FFT based RT is however not straitforward because we need to interpolate the Fourier domain. Furthermore, if we want to have an exact inverse transform, we have to make sure that the lines pass through all frequencies.

For our implementation, we use a pseudo-polar grid. The geometry of the rectopolar grid is illustrated in Fig. 3. We select 2 n radial lines in the frequency plane obtained by connecting the origin to the vertices (k₁,k₂) lying on the boundary of the array (k₁, k₂), i.e. such that k₁ or $k_2 \in \{-n/2, n/2\}$. The polar grid $\xi_{\ell,m}$ ($\ell$ serves to index a given radial line while the position of the point on that line is indexed by m) that we shall use is the intersection between the set of radial lines and that of cartesian lines parallel to the axes. To be more specific, the sample points along a radial line ${\cal L}$ whose angle with the vertical axis is less or equal to $\pi/4$ are obtained by intersecting ${\cal L}$ with the set of horizontal lines $\{x_2 = k_2, ~ k_2 = -n/2, -n/2 + 1, \ldots, n/2\}$. Similarly, the intersection with the vertical lines $\{x_1 = k_1, ~ k_1 = -n/2, -n/2 + 1, \ldots, n/2\}$defines our sample points whenever the angle between ${\cal L}$ and the horizontal axis is less or equal to $\pi/4$. The cardinality of the rectopolar grid is equal to 2 n² as there are 2 n radial lines and n sampled values on each of these lines. As a result, data structures associated with this grid will have a rectangular format. We observe that this choice corresponds to irregularly spaced values of the angular variable $\theta$. More details can be found in Starck et al. (2002).

Figure 3: Illustration of the digital polar grid in the frequency domain for an n by n image (n=8). The figure displays the set of radial lines joining pairs of symmetric points from the boundary of the square. The rectopolar grid is the set of points - marked with circles - at the intersection between those radial lines and those which are parallel to the axes.

2.2.2 1D wavelet transform

To complete the ridgelet transform, we must take a one-dimensional wavelet transform along the radial variable in Radon space. We now discuss the choice of digital one-dimensional wavelet transform.

Experience has shown that compactly-supported wavelets can lead to many visual artifacts when used in conjunction with nonlinear processing - such as hard-thresholding of individual wavelet coefficients - particularly for decimated wavelet schemes used at critical sampling. Also, because of the lack of localization of such compactly-supported wavelets in the frequency domain, fluctuations in coarse-scale wavelet coefficients can introduce fine-scale fluctuations; this is undesirable in our setting. Here we take a frequency-domain approach, where the discrete Fourier transform is reconstructed from the inverse Radon transform. These considerations lead us to use band-limited wavelet - whose support is compact in the Fourier domain rather than the time-domain. Other implementations have made a choice of compact support in the frequency domain as well (Donoho 1998; Donoho 1997). However, we have chosen a specific overcomplete system, based on the work of Starck et al. (1994, 1998), who constructed such a wavelet transform and applied it to interferometric image reconstruction. The wavelet transform algorithm is based on a scaling function $\phi$ such that $\hat{\phi}$ vanishes outside of the interval $[-\nu_{\rm c}, \nu_{\rm c}]$. We defined the scaling function $\hat{\phi}$ as a renormalized B₃-spline

$$\begin{eqnarray*}\hat{\phi}(\nu)= {3\over 2} B_3(4\nu), \end{eqnarray*}$$

and $\hat{\psi}$ as the difference between two consecutive resolutions

$$\begin{eqnarray*}\hat \psi(2\nu) = \hat \phi(\nu) - \hat \phi(2\nu). \end{eqnarray*}$$

Because $\hat{\psi}$ is compactly supported, the sampling theorem shows than one can easily build a pyramid of $n + n/2 + \ldots + 1 = 2n$ elements, see (Starck et al. 1998) for details.

Figure 4: Ridgelet transform flowgraph. Each of the 2n radial lines in the Fourier domain is processed separately. The 1-D inverse FFT is calculated along each radial line followed by a 1-D nonorthogonal wavelet transform. In practice, the one-dimensional wavelet coefficients are directly calculated in the Fourier space.

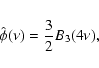
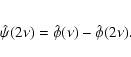
This transform enjoys the following features:

• The wavelet coefficients are directly calculated in the Fourier space. In the context of the ridgelet transform, this allows avoiding the computation of the one-dimensional inverse Fourier transform along each radial line.
• Each subband is sampled above the Nyquist rate, hence, avoiding aliasing - a phenomenon typically encountered by critically sampled orthogonal wavelet transforms (Simoncelli et al. 1992).
• The reconstruction is trivial. The wavelet coefficients simply need to be co-added to reconstruct the input signal at any given point. In our application, this implies that the ridgelet coefficients simply need to be co-added to reconstruct Fourier coefficients.

This wavelet transform introduces an extra redundancy factor, which might be viewed as an objection by advocates of orthogonality and critical sampling. However, we note that our goal in this implementation is not data compression/efficient coding - for which critical sampling might be relevant - but instead noise removal, for which it well-known that overcompleteness can provide substantial advantages (Coifman & Donoho 1995).

Figure 4 shows the flowgraph of the ridgelet transform. The ridgelet transform of an image of size $n \times n$ is an image of size $2n \times 2n$, introducing a redundancy factor equal to 4.

We note that, because our transform is made of a chain of steps, each one of which is invertible, the whole transform is invertible, and so has the exact reconstruction property. For the same reason, the reconstruction is stable under perturbations of the coefficients.

Last but not least, our discrete transform is computationally attractive. Indeed, the algorithm we presented here has low complexity since it runs in ${\rm O}(n^2\log(n))$ flops for an $n \times n$ image.

The ridgelet transform of a digital array of size $n \times n$ is an array of size $2n \times 2n$ and hence introduces a redundancy factor equal to 4.

2.3 Local ridgelet transforms

The ridgelet transform is optimal to find only lines of the size of the image. To detect line segments, a partitioning must be introduced (Candès 1998). The image is decomposed into smoothly overlapping blocks of sidelength b pixels in such a way that the overlap between two vertically adjacent blocks is a rectangular array of size b by b/2; we use overlap to avoid blocking artifacts. For an n by n image, we count 2n/b such blocks in each direction.

The partitioning introduces redundancy, as a pixel belongs to 4 neighboring blocks. We present two competing strategies to perform the analysis and synthesis:

1.

The block values are weighted (analysis) in such a way that the co-addition of all blocks reproduce exactly the original pixel value (synthesis).

2.

The block values are those of the image pixel values (analysis) but are weighted when the image is reconstructed (synthesis).

Experiments have shown that the second approach leads to better results. We calculate a pixel value, f(i,j) from its four corresponding block values of half-size $\ell = b/2$, namely, B₁(i₁,j₁), B₂(i₂,j₁), B₃(i₁,j₂) and B₄(i₂,j₂) with i₁, j₁ > b/2 and $i_2 = i_1 - \ell, j_2 = j_1- \ell$, in the following way:

$$f_1 = w(i_2/\ell) B_1(i_1,j_1) + w(1-i_2/\ell) B_2(i_2,j_1)$$

$$f_2 = w(i_2/\ell) B_3(i_1,j_2) + w(1-i_2/\ell) B_4(i_2,j_2)$$

$$f(i,j) = w(j_2/\ell) f_1 + w(1-j_2/\ell) f_2$$ (5)

with $w(x) = \cos^2~(\pi x/2)$. Of course, one might select any other smooth, nonincreasing function satisfying, w(0) = 1, w(1) = 0, w'(0) = 0 and obeying the symmetry property w(x) + w(1-x) = 1.

It is worth mentioning that the spatial partitioning introduces a redundancy factor equal to 4.

   
2.4 Digital curvelet transform

2.4.1 Definition

The curvelet transform (Donoho & Duncan 2000; Candès & Donoho 1999a; Starck et al. 2002), open us the possibility to analyze an image with different block sizes, but with a single transform. The idea is to first decompose the image into a set of wavelet bands, and to analyze each band by a local ridgelet transform. The block size can be changed at each scale level. Roughly speaking, different levels of the multiscale ridgelet pyramid are used to represent different subbands of a filter bank output. At the same time, this subband decomposition imposes a relationship between the width and length of the important frame elements so that they are anisotropic and obey width = length².

The discrete curvelet transform of a continuum function  f(x₁,x₂) makes use of a dyadic sequence of scales, and a bank of filters with the property that the passband filter $\Delta_s$ is concentrated near the frequencies [2^2s, 2^2s+2], e.g.

$$\begin{eqnarray*}\Delta_s = \Psi_{2s} * f, \quad \widehat{\Psi_{2s}}(\xi) = \widehat{\Psi}(2^{-2s}\xi). \end{eqnarray*}$$

In wavelet theory, one uses a decomposition into dyadic subbands [2^s, 2^s+1]. In contrast, the subbands used in the discrete curvelet transform of continuum functions have the nonstandard form [2^2s, 2^2s+2]. This is nonstandard feature of the discrete curvelet transform well worth remembering.

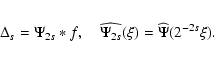
The curvelet decomposition is the sequence of the following steps:

• Subband decomposition. The object f is decomposed into subbands.
• Smooth partitioning. Each subband is smoothly windowed into "squares'' of an appropriate scale (of sidelength $\sim$2^-s).
• Ridgelet analysis. Each square is analyzed via the discrete ridgelet transform.

In this definition, the two dyadic subbands [2^2s, 2^2s+1] and  [2^2s+1, 2^2s+2] are merged before applying the ridgelet transform.

2.4.2 Digital realization

It seems that the "à trous'' subband filtering algorithm is especially well-adapted to the needs of the digital curvelet transform. The algorithm decomposes an n by n image I as a superposition of the form

$$\begin{eqnarray*}I(x,y) = c_{J}(x,y) + \sum_{j=1}^{J} w_j(x,y), \end{eqnarray*}$$

where c_J is a coarse or smooth version of the original image Iand w_j represents "the details of I'' at scale 2^-j, see Starck et al. (1998), Starck & Murtagh (2002) for more information. Thus, the algorithm outputs J+1 subband arrays of size $n \times n$. (The indexing is such that, here, j = 1 corresponds to the finest scale (high frequencies).)

Figure 5: Curvelet transform flowgraph. The figure illustrates the decomposition of the original image into subbands followed by the spatial partitioning of each subband. The ridgelet transform is then applied to each block.

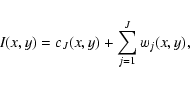
A sketch of the discrete curvelet transform algorithm is:

1.

apply the "à trous'' algorithm with J scales,

2.

set $B_1 = B_{{\rm min}}$,

3.

for $j = 1, \ldots, J$ do,

• partition the subband w_j with a block size B_j and apply the digital ridgelet transform to each block,
• if $j \mbox{ modulo } 2 = 1$ then B_j+1 = 2 B_j,
• else B_j+1 = B_j.

The sidelength of the localizing windows is doubled at every other dyadic subband, hence maintaining the fundamental property of the curvelet transform which says that elements of length about 2^-j/2 serve for the analysis and synthesis of the jth subband [2^j, 2^j+1]. Note also that the coarse description of the image c_J is not processed. We used the default value $B_{{\rm min}} = 16$ pixels in our implementation. Finally, Fig. 5 gives an overview of the organization of the algorithm.

This implementation of the curvelet transform is also redundant. The redundancy factor is equal to 16J+1 whenever J scales are employed. Finally, the method enjoys exact reconstruction and stability, because these invertibility holds for each element of the processing chain.