Utilizing the density models defined in Sect. 2 the frequencies
![]() are converted to radial distances Ri(ti),
where
are converted to radial distances Ri(ti),
where
![]() is the heliocentric distance normalized with
respect to the solar radius
is the heliocentric distance normalized with
respect to the solar radius ![]() .
The obtained values are
used to determine the radial velocities:
.
The obtained values are
used to determine the radial velocities:
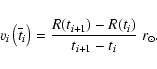 |
(6) |
The values vi(Ri) and
![]() are used to evaluate the
Alfvén velocity
are used to evaluate the
Alfvén velocity
![]() and the corresponding
magnetic field (Eq. (3)). The results are shown in Fig. 4
for the two-fold Newkirk density model so that the B(R)dependence can be compared with the results reported by Smerd et al. (1974, 1975) which are shown by gray
crosses in Fig. 4b.
and the corresponding
magnetic field (Eq. (3)). The results are shown in Fig. 4
for the two-fold Newkirk density model so that the B(R)dependence can be compared with the results reported by Smerd et al. (1974, 1975) which are shown by gray
crosses in Fig. 4b.
The
![]() dependence shows a local minimum at
dependence shows a local minimum at
![]() .
It is somewhat less exposed if the Saito model is applied (the values
based on the five-fold Saito model are shown in the inset of
Fig. 4a) due to a less steep slope of n(R) around that
distance (see Fig. 8 in the Appendix). However, whatever
polynomial fit is used, at least an inflection in the fitted curve
is found. We note that the results do not change significantly if
the two data points showing a comparatively high Alfvén velocity
at
.
It is somewhat less exposed if the Saito model is applied (the values
based on the five-fold Saito model are shown in the inset of
Fig. 4a) due to a less steep slope of n(R) around that
distance (see Fig. 8 in the Appendix). However, whatever
polynomial fit is used, at least an inflection in the fitted curve
is found. We note that the results do not change significantly if
the two data points showing a comparatively high Alfvén velocity
at
![]() are removed.
are removed.
In Figs. 5 and 6 the average values
![]() and
and
![]() are shown, where
each data point represents the mean of 40 distance-successive data
points. This representation is chosen to illustrate more
transparently how different choices of
are shown, where
each data point represents the mean of 40 distance-successive data
points. This representation is chosen to illustrate more
transparently how different choices of ![]() (Figs. 5a
and 6a), propagation angle
(Figs. 5a
and 6a), propagation angle ![]() (Figs. 5b and 6b), and a density model (Figs. 5c and 6c)
affect the results. Clearly, the results are most sensitive on the
choice of the density model. Figure 5 indicates again that
there is a local minimum, or at least a stagnation in the decrease
of
(Figs. 5b and 6b), and a density model (Figs. 5c and 6c)
affect the results. Clearly, the results are most sensitive on the
choice of the density model. Figure 5 indicates again that
there is a local minimum, or at least a stagnation in the decrease
of ![]() at
at
![]() .
.
The B(R) dependence can be approximated well by the power law
fit of the form
B(R)=a R-b. The results are summarized in Table 1 where the power-law coefficients a and b are given. In Table 1 we also show the coefficients for the power-law fit
expressing the magnetic field as a function of the normalized
height
![]() .
Inspecting Table 1 one finds that the Saito
model gives somewhat steeper decrease of the magnetic field with
the distance than the Newkirk model. If the magnetic field
decrease is expressed as a function of the height above the solar
surface, the slope is in the range
.
Inspecting Table 1 one finds that the Saito
model gives somewhat steeper decrease of the magnetic field with
the distance than the Newkirk model. If the magnetic field
decrease is expressed as a function of the height above the solar
surface, the slope is in the range
![]() -2, where the
former value corresponds to the two-fold Newkirk model. Similar
results are obtained if the averaged data shown in Fig. 6
are used, now with the correlation coefficients C>0.98.
-2, where the
former value corresponds to the two-fold Newkirk model. Similar
results are obtained if the averaged data shown in Fig. 6
are used, now with the correlation coefficients C>0.98.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{MS2984f4new.eps} \end{figure}](/articles/aa/full/2002/47/aa2984/Timg80.gif) |
Figure 4:
a) Alfvén velocity and b) magnetic field,
evaluated assuming the perpendicular shock propagation (
|
![\begin{figure}
\par\includegraphics[width=8.6cm,clip]{MS2984f6new.eps} \end{figure}](/articles/aa/full/2002/47/aa2984/Timg82.gif) |
Figure 6:
Magnetic field shown as a function of heliocentric distance for
the same combinations of parameters as used in Fig. 5.
The |
Copyright ESO 2002