

Up: Band-splitting of coronal and
In the presented analysis we have used different
approximations and assumptions. In Fig. 8 the density
models used are shown. The two-fold Newkirk, two-, five-, and
ten-fold Saito models are denoted in the legend of Fig. 8
as 2xNewk., 2xSaito, 5xSaito and 10xSaito.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{MS2984f8new.eps} \end{figure}](/articles/aa/full/2002/47/aa2984/Timg102.gif) |
Figure 8:
The coronal density models used. |
The relationship between the downstream/upstream density jump X(compression) and the Alfvén Mach number 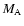 depends on the
plasma-to-magnetic pressure ratio
depends on the
plasma-to-magnetic pressure ratio 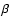 and the angle
and the angle 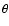 between the shock normal and the upstream magnetic field. For the
oblique shock the Alfvén Mach number
between the shock normal and the upstream magnetic field. For the
oblique shock the Alfvén Mach number 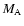 and the density jump
X are related (taking for the adiabatic index
and the density jump
X are related (taking for the adiabatic index
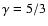 )
as:
)
as:
![\begin{displaymath}%
\begin{array}{l}
\left(M_{{\rm A}x}^2 - X\right)^2~\left[5\...
...heta~\left[(5+X)M_{{\rm A}x}^2 + 2X(X-4)\right]=0.
\end{array}\end{displaymath}](/articles/aa/full/2002/47/aa2984/img104.gif) |
(7) |
Here
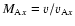 is the Alfvén Mach number based on the
is the Alfvén Mach number based on the
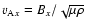 component of the Alfvén velocity,
where Bx=Bcos
component of the Alfvén velocity,
where Bx=Bcos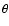 is the magnetic field component normal to
the shock front (e.g., Mann et al. 1995). Since the sound
speed and the Alfvén velocity are related as
is the magnetic field component normal to
the shock front (e.g., Mann et al. 1995). Since the sound
speed and the Alfvén velocity are related as
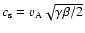 the sound Mach number can be also
determined:
the sound Mach number can be also
determined:
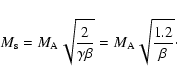 |
(8) |
In the case of the perpendicular shock (
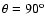 )
Eq. (7) becomes:
)
Eq. (7) becomes:
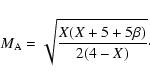 |
(9) |
In the limiting case, for
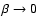 one finds:
one finds:
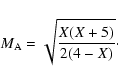 |
(10) |
On the other side, for
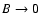 (i.e.
(i.e.
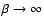 )
one comes to the hydrodynamic
approximation (sound shock wave), and the Mach number is:
)
one comes to the hydrodynamic
approximation (sound shock wave), and the Mach number is:
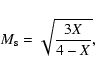 |
(11) |
which was used by Smerd et al. (1974, 1975).
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{MS2984f9new.eps} \end{figure}](/articles/aa/full/2002/47/aa2984/Timg115.gif) |
Figure 9:
Relationship between the Alfvén Mach number 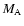 and the relative band-split BDW obtained from
and the relative band-split BDW obtained from
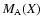 relationship by substituting
relationship by substituting
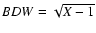 (see Eq. (2)). Results are presented for
a) different angles
(see Eq. (2)). Results are presented for
a) different angles 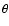 between the shock normal and the magnetic
field, with
between the shock normal and the magnetic
field, with 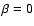 ;
b) different values of plasma-to-magnetic field pressure ratio ;
b) different values of plasma-to-magnetic field pressure ratio
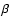 for the perpendicular shock, as well as for the
hydrodynamic shock (gray line).
for the perpendicular shock, as well as for the
hydrodynamic shock (gray line). |
As Eqs. (7)-(11) show, the compression is limited
to X<4, corresponding to
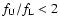 ,
i.e., BDW<1,
regardless on the value of
,
i.e., BDW<1,
regardless on the value of 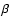 .
.
In the case of the longitudinal shock (
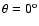 ):
):
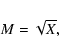 |
(12) |
but there is an upper limit on the compression which depends on
the value of 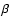 :
:
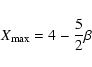 |
(13) |
(Priest 1982).
The relationships given by Eqs. (7)-(12) are illustrated in
Fig. 9 for different combinations of 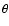 and
and 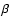 .
.


Up: Band-splitting of coronal and
Copyright ESO 2002
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{MS2984f8new.eps} \end{figure}](/articles/aa/full/2002/47/aa2984/Timg102.gif)
![]() depends on the
plasma-to-magnetic pressure ratio
depends on the
plasma-to-magnetic pressure ratio ![]() and the angle
and the angle ![]() between the shock normal and the upstream magnetic field. For the
oblique shock the Alfvén Mach number
between the shock normal and the upstream magnetic field. For the
oblique shock the Alfvén Mach number ![]() and the density jump
X are related (taking for the adiabatic index
and the density jump
X are related (taking for the adiabatic index
![]() )
as:
)
as:
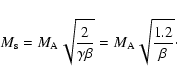
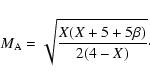
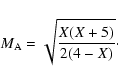
![]() ,
i.e., BDW<1,
regardless on the value of
,
i.e., BDW<1,
regardless on the value of ![]() .
.
![]() ):
):
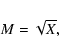
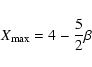
![]() and
and ![]() .
.