In this paper we investigate 18 coronal type II bursts recorded in
the decimetric-metric (dm-m) wavelength range. The basic rule in
selecting the events was that they clearly show a simple
band-split pattern obeying the criteria defined in Paper I. Out of
the 18 chosen events, 12 events were recorded by the radio
spectrograph of the Astrophysikalisches Institut Potsdam
covering the frequency range 40-800 MHz (Mann et al. 1992) and 6 were observed by Culgoora Solar
Observatory radio spectrograph sweeping over the frequency range
18-1800 MHz (Prestage et al. 1994; see http://www.ips.oz.au/culgoora/spectro/index.html). The
measurements were performed at the harmonic emission
band![]() since in dm-m type II
bursts it is usually stronger and better defined then the
fundamental band (see, e.g., Fig. 1 where a part of the
fundamental band can be seen in the 50-40 MHz range around
10:00 UT). In some cases measurements of equal accuracy were
possible at both emission bands, showing no significant difference
in the outcome (see also Smerd et al. 1974,
1975; Mann et al. 1996).
since in dm-m type II
bursts it is usually stronger and better defined then the
fundamental band (see, e.g., Fig. 1 where a part of the
fundamental band can be seen in the 50-40 MHz range around
10:00 UT). In some cases measurements of equal accuracy were
possible at both emission bands, showing no significant difference
in the outcome (see also Smerd et al. 1974,
1975; Mann et al. 1996).
In Fig. 1 the procedure of measurements is illustrated by
showing one of the analysed type II bursts (see also Fig. 2
in Paper I). The LFB and UFB of the band-split emission are marked
by the lines that follow the two emission ridges. The period of
type II burst emission is divided into a number of roughly
equidistant subintervals, defined by the times t1 to tN. At each of these N moments the frequencies of the emission maximum
at LFB and UFB (![]() and
and ![]() ,
respectively) were
measured, providing the relative band-splits BDW(ti) defined by
Eq. (1).
,
respectively) were
measured, providing the relative band-splits BDW(ti) defined by
Eq. (1).
The number of
![]() ,
,
![]() data pairs
varied from 3 to 22 per event, depending on the duration and
frequency range covered by a particular type II burst. From the
obtained data the frequency drifts:
data pairs
varied from 3 to 22 per event, depending on the duration and
frequency range covered by a particular type II burst. From the
obtained data the frequency drifts:
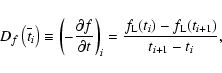 |
(4) |
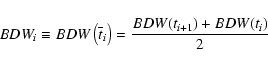 |
(5) |
Figure 2a shows that the frequency drift is a distinct
power-law function of the frequency. In Paper I it was shown that
the power-law dependence Df(f) extends to the kilometric
wavelength range. The slope of Df(f) found therein for the
frequency range from 10 MHz to 30 kHz is almost the same,
amounting to ![]() 1.9.
1.9.
Figure 2b shows no correlation between the band-split of metric type II bursts and the frequency. In the inset of Fig. 2b the distribution of values of BDW is presented showing that the majority of the analysed type II bursts has the relative band-split between 0.15 and 0.35.
Copyright ESO 2002