

Up: Precise reduction of solar
Subsections
The reduction of the solar spectra should improve the S/N ratio in the spectra
but on the other hand the shape of the spectral lines must be not affected.
Therefore we tested both the noise propagation through the data and analysis
of corrupting of the shape of the spectral lines.
First, the standard deviations of different types of arrays were computed and
secondly, the accuracy of the spectral characteristics determined from the
simple, extended and precise reductions was examined.
Generally noisy data have a higher standard deviation of the signal then the good data.
This is not the case for the solar spectra.
One must distinguish between the noise coming from defects and noisy flats and between
the real physical variations of the intensity across the image.
For example the best solar spectra of the solar granulation reach a standard deviation
of the intensity variation along the slit between 6%-7% after
reduction. Therefore, it is important to analyze if the standard deviation
was decreased by the reduction process and not to be afraid of the big standard deviation
of the resulting spectra.
The standard deviations of the signal of the original as well as of the reduced spectra
are given in Table 2 and the standard deviation of the signal of the "supporting''
arrays (G, F, M) are shown in Table 3.
We estimated the standard deviations only from a limited area of any spectral array,
to exclude the contribution of the spectral lines to the values.
An area was selected in the upper right corner of the arrays, marked
by the rectangular box in the array in Fig. 5.
Because of the absence of spectral lines in the flat-field matrix M the calculation
of the standard deviations in these arrays (the last four column in Table 3)
was done in the whole area between the wires WL.
We will discuss these results in Sect. 6.
The stability of the shape of the spectral lines was tested using spectral characteristics
of the spectra Rk, k=1, 2, 3 resulting from the simple, extended and
precise reduction respectively. Only 946 scans selected between the WL wires were
used for the analysis.
Several manipulations were applied to every scan of the Rk before
the spectral characteristics were calculated:
a) the local continuum of every scan was determined on the left and right side
of the spectral line
as a maximum of the second order polynomial fit of selected intervals of intensities.
Because of the very small spectral region recorded on the CCD chip (no true continuum level available beside the lines), these intervals are not the 100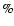 continua valid for
this spectral region.
They could be recalculated to the true continua using the solar spectrum atlas.
The intensity of the "quasi-continuum'' interval available beside the lines in the
spectrum is compared with the intensity of the same interval available in the solar atlas.
The ratio between them serves for correction.
But for our purpose, to compare the relative difference of spectral
characteristics, this was not necessary;
continua valid for
this spectral region.
They could be recalculated to the true continua using the solar spectrum atlas.
The intensity of the "quasi-continuum'' interval available beside the lines in the
spectrum is compared with the intensity of the same interval available in the solar atlas.
The ratio between them serves for correction.
But for our purpose, to compare the relative difference of spectral
characteristics, this was not necessary;
b) Fast Fourier Transform was used for high frequency signal filtering to smooth data
of every scan.
Optional Gaussian filtering of high frequency noise (cf. Gray 1992) has effectively
filtered all power above 1/10 of the Nyquist frequency;
c) the zero position for determination of shifts of line centres and bisectors was
calculated as the position of the centre of the mean profile. The mean profile was
constructed as an average of the 946 profiles;
d) a spectral line inclination in R1 which resulted from the simple
flat-fielding was eliminated, i.e. we applied de-stretching after the flat-fielding
in this case.
The spectral characteristics, continuum intensity (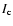 ), line centre
intensity (
), line centre
intensity (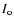 ), line Doppler shift (
), line Doppler shift (
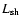 ), bisectors Bi and full width
at half maximum (FWHM) were calculated separately for every scan for all three
types of resulting spectra
), bisectors Bi and full width
at half maximum (FWHM) were calculated separately for every scan for all three
types of resulting spectra 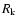 .
In Fig. 9 the line center intensity fluctuations
.
In Fig. 9 the line center intensity fluctuations 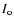 along the slit
(Y direction) resulting from precise, extended and simple reduction
are shown.
For comparison of the results we used the differences of the spectral characteristics.
We use the results given by the precise flat-fielding as a standard for the
estimation of the relative errors of the values resulting from the other two reduction
approaches.
The relative differences of the line centre intensities RD3,i, (i=1, 2) expressed
as a percentage were calculated as:
along the slit
(Y direction) resulting from precise, extended and simple reduction
are shown.
For comparison of the results we used the differences of the spectral characteristics.
We use the results given by the precise flat-fielding as a standard for the
estimation of the relative errors of the values resulting from the other two reduction
approaches.
The relative differences of the line centre intensities RD3,i, (i=1, 2) expressed
as a percentage were calculated as:
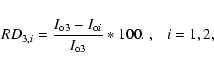 |
(14) |
and the mean of the result was normalized to a value of 0.0.
The relative differences of 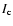 and of FWHM were calculated in the same way.
The results are shown in Fig. 10.
and of FWHM were calculated in the same way.
The results are shown in Fig. 10.
![\begin{figure}
\par\resizebox{\hsize}{!}{\includegraphics[width=8cm,height=4cm]{...
...x{\hsize}{!}{\includegraphics[width=8cm,height=4cm]{MS2154f17.eps}}
\end{figure}](/articles/aa/full/2002/42/aa2154/Timg70.gif) |
Figure 9:
Line centre intensity fluctuations 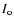 along the slit
(Y direction)
resulting from:
a) precise, b) extended and c) simple flat-fielding.
The difference of the first and third panel is shown in Fig. 10b and
the difference of the first and second panel is shown in Fig. 10e.
along the slit
(Y direction)
resulting from:
a) precise, b) extended and c) simple flat-fielding.
The difference of the first and third panel is shown in Fig. 10b and
the difference of the first and second panel is shown in Fig. 10e.
|
The absolute differences of the line centre shifts AD3,i, (i=1, 2) expressed
in m s-1 were calculated according to the equation:
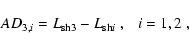 |
(15) |
where
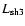 denotes the line shifts resulting from precise flat-fielding
(spectrum
denotes the line shifts resulting from precise flat-fielding
(spectrum 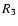 ), and
), and
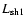 and
and
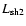 denote the line centre shifts
resulting from simple flat-fielding (spectrum
denote the line centre shifts
resulting from simple flat-fielding (spectrum 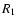 )
and from
extended flat-fielding (spectrum
)
and from
extended flat-fielding (spectrum 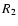 ), respectively.
The results are shown in Fig. 11.
), respectively.
The results are shown in Fig. 11.
The absolute differences of bisectors Bi were calculated in the same way
as for the line shifts and the results for bisectors at 0.2, 0.4, and 0.6 of
the line intensity are shown in Fig. 12.


Up: Precise reduction of solar
Copyright ESO 2002
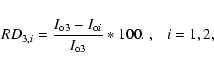
![\begin{figure}
\par\resizebox{\hsize}{!}{\includegraphics[width=8cm,height=4cm]{...
...x{\hsize}{!}{\includegraphics[width=8cm,height=4cm]{MS2154f17.eps}}
\end{figure}](/articles/aa/full/2002/42/aa2154/Timg70.gif)