

Up: Precise reduction of solar
Subsections
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{MS2154f2.eps}
\end{figure}](/articles/aa/full/2002/42/aa2154/Timg32.gif) |
Figure 2:
The mean flat-field frame
 as constructed using Eq. (9)
with K =40.
WL = pictures of the artificial wires put on
the spectrograph slit; SL = spectral lines;
TL = terrestrial spectral line;
DL = "dust'' lines caused by dust particles lying on the slit;
IP = imperfections coming mainly from invalid pixels of the CCD chip.
Inclination and stretching of the spectral line(s) and inclination
of the horizontal wires are pointed out by the white vertical and horizontal
lines, respectively.
Different
sensitivities of the four segments of the chip are obvious. The grey-scale
bar gives relative intensities expressed in ADU.
as constructed using Eq. (9)
with K =40.
WL = pictures of the artificial wires put on
the spectrograph slit; SL = spectral lines;
TL = terrestrial spectral line;
DL = "dust'' lines caused by dust particles lying on the slit;
IP = imperfections coming mainly from invalid pixels of the CCD chip.
Inclination and stretching of the spectral line(s) and inclination
of the horizontal wires are pointed out by the white vertical and horizontal
lines, respectively.
Different
sensitivities of the four segments of the chip are obvious. The grey-scale
bar gives relative intensities expressed in ADU. |
We describe in detail all the steps
(sometimes rather trivial)
of the reduction process to keep an instructive scheme of the whole
one. Spectral characteristics at three different steps of the
reduction process were retrieved to demonstrate an increase in
the precision of the
results by using more precise steps of reduction.
The precise reduction process
consists of:
-
1. subtraction of the background G from the particular raw spectrum P;
-
2. construction of the mean flat-field frame
 ;
;
-
3. extraction of the segment-flat M6 from the mean flat-field
frame
 ;
;
- 4. retrieving of the components
M1,2,3,4,5 from the mean flat-field
frame
 ;
;
- 4.1 precise restoration of the X inclination of the image;
-
4.2 de-stretching - the restoration of the curvature and Y inclination of the spectral line;
-
4.3 construction of the flat-field matrix M;
-
4.4 extracting the slit-flat M5 from the flat-field matrix M;
-
4.5 shift of the slit-flat M5;
-
5. flat-fielding.
In the simple approach of the flat-fielding we omitted the steps 4.1, 4.2, 4.4, and 4.5.
This means that the flat-fielding was done with the flat-field matrix M which was
constructed directly from the raw mean flat-field frame
 (cf. Fig. 2) corrected for the segment-flat M6.
In the extended approach of the flat-fielding we omitted step 4.5.
The consequence is that the flat-field matrix M is shifted compared to
the spectrum S.
(cf. Fig. 2) corrected for the segment-flat M6.
In the extended approach of the flat-fielding we omitted step 4.5.
The consequence is that the flat-field matrix M is shifted compared to
the spectrum S.
The reduction was performed with programs written in the Interactive Data
Language (IDL) using also the IDL KIS package at the Kiepenheuer-Institut
für Sonnenphysik, Freiburg.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{MS2154f3.eps}
\end{figure}](/articles/aa/full/2002/42/aa2154/Timg34.gif) |
Figure 3:
Average background
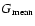 belonging to the spectra
in Figs. 1 and 2. The grey-scale bar gives relative
intensities expressed in ADU.
Segment numbers are denoted inside the figure.
belonging to the spectra
in Figs. 1 and 2. The grey-scale bar gives relative
intensities expressed in ADU.
Segment numbers are denoted inside the figure. |
In real spectra, the background G given in the Eqs. (1), (2),
(4) and (5) consists of the noise of the CCD camera (dark current D),
of the bias B, introduced by the readout electronics of the CCD and of the scattered
light L coming from the spectrograph with a closed shutter.
As was mentioned in Sect. 2, the background G can vary during the observation.
The bias B varies with temperature, so the best way to keep it constant is to use
the cooling control of the CCD camera. If this is not the case, one must estimate
the sensitivity of the bias B to the temperature changes experimentally and then
use an appropriate background G image according to the actual temperature during
the acquisition of the spectra.
Measurement of the background G should also be repeated if any change of the setup of
the instrument was done concerning the change of the scattered light in the instrument.
To keep the S/N ratio as high as possible it is useful to average several background G frames (see Newberry 1991, for a more detailed description of signal-to
noise considerations).
Thus, the Eq. (4) takes the
following form:
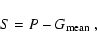 |
(6) |
where
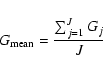 |
(7) |
is the average of several particular background images G including
the dark current D, bias B and scattered light L.
The background G was stable during the whole observation run because the CCD camera
was equipped with a cooling control.
Therefore we used the average of the first 7 background images G for corrections.
An example of
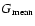 is demonstrated in Fig. 3.
The mean value of the intensity of the
is demonstrated in Fig. 3.
The mean value of the intensity of the
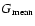 was 44.96 ADU. 100 ADU
was automatically added to every background frame (as well as to all other frames)
to avoid negative values.
The segments I, II, III and IV, denoted in Fig. 3, had relative intensities
to the mean 0.636, 1.227, 0.978 and 1.150, respectively.
Different intensities of the segments are due to different bias, i.e. due to nonuniform
readout of the electronics of the four segments.
Each particular raw spectrum P as well as flat-field source frame F was corrected for
was 44.96 ADU. 100 ADU
was automatically added to every background frame (as well as to all other frames)
to avoid negative values.
The segments I, II, III and IV, denoted in Fig. 3, had relative intensities
to the mean 0.636, 1.227, 0.978 and 1.150, respectively.
Different intensities of the segments are due to different bias, i.e. due to nonuniform
readout of the electronics of the four segments.
Each particular raw spectrum P as well as flat-field source frame F was corrected for
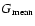 .
In this section we will deal with the difficulties of taking flat field source
frames F and mean flat-field frame
.
In this section we will deal with the difficulties of taking flat field source
frames F and mean flat-field frame
 that serve as the basis for the
computation of the flat-field matrix M.
We will focus on the special case of a solar spectra taken with a large CCD array.
that serve as the basis for the
computation of the flat-field matrix M.
We will focus on the special case of a solar spectra taken with a large CCD array.
As we stated in Sect. 2, the flat-field is used to correct both the non-uniform
response across the surface of the chip and non-uniform illumination of the chip.
Therefore, it is not enough to illuminate the chip with uniform light and use the
resultant exposure for correction.
The uniform light must pass through the complete optical system with an identical
focus, exposure time and other conditions as those valid for every particular spectrum P.
Moreover, the spectral range of the flat-field source frame F should match that of
the object being imaged.
Therefore, for solar CCD spectroscopy, the ideal source for flat-fielding
should be at infinity, should be a source similar to sunlight and the light must
pass through the telescope and spectrograph.
From these last requirements it is clear that it is impossible to get ideal artificial
uniform light from infinity for flat-fielding in this case and the Sun itself is the only
source intensive enough to mimic observational conditions.
Thus, the flat-field source frames F must be derived from images that are almost
identical to the particular raw spectrum P.
There are several ways to create the flat-field source frames Fin this case:
a) the simplest way is to sandwich all particular raw P images we made and
get an average "soft'' spectrum with smoothed spectral line(s);
b) the second possibility is to de-focus the telescope and to make
enough un-sharp images.
Then we construct the average of them to obtain a similar
result to the previous case;
c) The third method of creation of the flat-field source frame F is to
move the image of the Sun across the slit in the focal plane of the telescope
and take a lot of images.
The average of such images will give a similar result to the previous two cases, because the
spectral lines will be smeared due to the fast movement
of the solar image across the spectrograph slit.
It is also possible to use a combination of the second and third methods
(e.g. Johannesson et al. 1992).
It is useful to take the flat-field source frames F very often, to minimize
the influence of the temporal changes of the flat-field conditions.
Many cases of observations do not allow us to make flat-field source frames F very often.
For example, the simultaneous observations with VTT and space instruments or
investigation of temporal changes in the solar atmosphere require uninterrupted long
series of observations.
Then, one can take the flat-field source frames F only at the beginning and at the end
of the observing run.
So the temporal changes of the flat-field conditions introduce rather serious problems
for the reduction of these spectra.
It is clearly seen, from the methods mentioned above, that all non-uniform illuminations
of the chip in the case of large solar spectra are grouped together into one mean
flat-field frame
 .
Namely, the
.
Namely, the
 for the first (sandwiching) method will be defined
as:
for the first (sandwiching) method will be defined
as:
![\begin{displaymath}F_{\rm mean} = \frac{\sum_{k=1}^{K} [P_k-G_{\rm mean}]}{K},
\end{displaymath}](/articles/aa/full/2002/42/aa2154/img38.gif) |
(8) |
where K is the number of all particular raw spectra P and
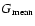 is the
mean background.
For the second and third methods the
is the
mean background.
For the second and third methods the
 is given by:
is given by:
![\begin{displaymath}F_{\rm mean} = \frac{\sum_{k=1}^{K} [F_k-G_{\rm mean}]}{K},
\end{displaymath}](/articles/aa/full/2002/42/aa2154/img39.gif) |
(9) |
where K is the number of the flat-field source frames F taken with de-focused telescope
and/or with moving solar image across the focal plane of the telescope.
However, all three methods for the construction of
 have some limitations.
Usually, one tries to observe the long series during the best seeing conditions,
keeping the spectrograph slit in the same position of the solar disk or scanning
within small areas.
Thus, the average of many raw spectra P still exhibits shifted patterns which remain
from the real Doppler velocity shifts of a particular part of every particular
raw spectrum P.
This results in non-uniform
have some limitations.
Usually, one tries to observe the long series during the best seeing conditions,
keeping the spectrograph slit in the same position of the solar disk or scanning
within small areas.
Thus, the average of many raw spectra P still exhibits shifted patterns which remain
from the real Doppler velocity shifts of a particular part of every particular
raw spectrum P.
This results in non-uniform
 in the case of the first method.
The second method with the de-focused telescope tends to optically disturb the spectrum
giving rise to lateral displacement of the location of the spectral line(s) in the
image plane in the camera and changes the fixed pattern, particularly the variations
due to fringing and illumination.
A similar displacement of the spectral lines could appear when one moves the telescope,
if the scanned area at the solar disc is very large.
This smears the spectral line due to averaging of shifted lines caused by real
differential rotation of the Sun.
in the case of the first method.
The second method with the de-focused telescope tends to optically disturb the spectrum
giving rise to lateral displacement of the location of the spectral line(s) in the
image plane in the camera and changes the fixed pattern, particularly the variations
due to fringing and illumination.
A similar displacement of the spectral lines could appear when one moves the telescope,
if the scanned area at the solar disc is very large.
This smears the spectral line due to averaging of shifted lines caused by real
differential rotation of the Sun.
We used the third method for construction of the mean flat-field frame
 .
The quick movement of the telescope was kept very near to the disc centre in a quiet
region to minimize the mentioned above displacement effects in every particular
flat-field source frame F.
The final
.
The quick movement of the telescope was kept very near to the disc centre in a quiet
region to minimize the mentioned above displacement effects in every particular
flat-field source frame F.
The final
 was an average of 40 particular flat-field source frames Ffrom which
was an average of 40 particular flat-field source frames Ffrom which
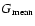 had previously been subtracted.
The mean flat-field frame
had previously been subtracted.
The mean flat-field frame
 is given in Fig. 2 with a description
of the most important features in the spectrum. Identical features also appear in
the raw spectrum P shown in Fig. 1.
The
is given in Fig. 2 with a description
of the most important features in the spectrum. Identical features also appear in
the raw spectrum P shown in Fig. 1.
The
 contains all six flat-fields Mi mentioned in Sect. 2,
and also the spectral lines as a consequence of the facts discussed in the beginning
of this section.
In the following sections we show how to retrieve the particular Mi from
the mean flat-field frame
contains all six flat-fields Mi mentioned in Sect. 2,
and also the spectral lines as a consequence of the facts discussed in the beginning
of this section.
In the following sections we show how to retrieve the particular Mi from
the mean flat-field frame
 .
.
 |
Figure 4:
a)
An incorrect flat-field matrix M2,3 composed of the
illumination-flat and the shutter-flat
as a resultant from the mean flat-field frame
 which was not corrected for stretching and inclination of
the spectral lines. The grey-scale
bar gives relative
intensities normalized to 1; b)
The stretching and inclination of the spectral lines determined in
Sect. 4.4.2.
Fluctuations of the centres of the spectral profiles along the
spectrograph slit
are shown by the thin line and
the polynomial approximation is represented by the thick line.
which was not corrected for stretching and inclination of
the spectral lines. The grey-scale
bar gives relative
intensities normalized to 1; b)
The stretching and inclination of the spectral lines determined in
Sect. 4.4.2.
Fluctuations of the centres of the spectral profiles along the
spectrograph slit
are shown by the thin line and
the polynomial approximation is represented by the thick line. |
The chip is composed of four independent parts which differ in sensitivity.
Therefore, the segment-flat M6 that bears only this differences is not
affected by the presence of the spectral lines in the mean flat-field frame
 .
So, it is possible and useful to extract the M6 from the mean flat-field
frame
.
So, it is possible and useful to extract the M6 from the mean flat-field
frame
 before further image manipulation.
In addition, the segment-flat M6 has fixed geometrical, rectangular stability
and further manipulations of the mean flat-field frame
before further image manipulation.
In addition, the segment-flat M6 has fixed geometrical, rectangular stability
and further manipulations of the mean flat-field frame
 ,
which are
described in the following subsections, would change the geometry of the segments.
On the other hand, if the mean flat-field frame
,
which are
described in the following subsections, would change the geometry of the segments.
On the other hand, if the mean flat-field frame
 were not corrected
for the segment-flat M6 before applying of the smoothing procedures required
for rubbing out the spectral lines, the different intensities of the segments of the
flat-field frame
were not corrected
for the segment-flat M6 before applying of the smoothing procedures required
for rubbing out the spectral lines, the different intensities of the segments of the
flat-field frame
 would affect the smoothing procedure.
In fact the four segments of the CCD chip also differ in the bias B,
but this was already compensated for in Sect. 4.1.
would affect the smoothing procedure.
In fact the four segments of the CCD chip also differ in the bias B,
but this was already compensated for in Sect. 4.1.
Because the flat-field M6 is uniform within every sub-segment, it is enough to
estimate the ratios of sensitivities between them and simply construct the
segment-flat matrix M6 as a matrix of four subsegments with appropriate ratios
of sensitivities between them.
We experimentally determined the sensitivities of the segments which are equal to 1.004, 1.029, 0.930 and 1.037 for segment I, II, III and IV, respectively, comparing
to the mean intensity of the whole chip, normalized to unity.
The designation of the segments is identical as in Fig. 3.
We have found the stability of the sensitivity of the individual segments to be within
the range of 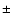 0.1% for the intensity range of 400-3200 ADU.
Obtaining the segment-flat M6, it was possible to correct the mean flat-field
frame
0.1% for the intensity range of 400-3200 ADU.
Obtaining the segment-flat M6, it was possible to correct the mean flat-field
frame
 by dividing it by M6.
Logically, the spectrum S was also corrected in the same way at this stage of the
reduction process.
We will name this improved spectrum S1.
It will be used in the simple reduction approach.
by dividing it by M6.
Logically, the spectrum S was also corrected in the same way at this stage of the
reduction process.
We will name this improved spectrum S1.
It will be used in the simple reduction approach.
First, several manipulations with the mean flat-field frame
 will be
done in this section, to prepare it for a correct derivation of the flat-field matrices.
Then, we will define the flat-field matrix M which is composed of five (
M1,2,3,4,5) components.
The elimination of the spectral lines from the flat-field matrix M will be described
and finally each particular flat-field matrix will be extracted from the mean
flat-field frame
will be
done in this section, to prepare it for a correct derivation of the flat-field matrices.
Then, we will define the flat-field matrix M which is composed of five (
M1,2,3,4,5) components.
The elimination of the spectral lines from the flat-field matrix M will be described
and finally each particular flat-field matrix will be extracted from the mean
flat-field frame
 .
.
It was possible to extract the segment-flat M6 from the mean flat-field
frame
 even when the spectral lines were presented.
This is not the case in the other flat-field matrices.
The spectral lines constrain the flat-field matrices and we must erase them from
the
even when the spectral lines were presented.
This is not the case in the other flat-field matrices.
The spectral lines constrain the flat-field matrices and we must erase them from
the
 .
The smoothing processes used for retrieving the flat-field matrix M are applied to
spectra in both the X and Y directions in the image.
To run them correctly it is necessary to have the mean flat-field frame
.
The smoothing processes used for retrieving the flat-field matrix M are applied to
spectra in both the X and Y directions in the image.
To run them correctly it is necessary to have the mean flat-field frame
 (as well as the spectrum S1) parallel to both edges of the CCD camera.
(as well as the spectrum S1) parallel to both edges of the CCD camera.
The horizontal sharp lines in the particular raw spectrum P as well as in the mean
flat-field frame
 (see the inclined WL and DL in Figs. 1
and 2) are artificial and/or natural.
The artificial horizontal lines (WL) are images of wires placed on the spectrograph
slit to adjust spectra taken by different CCD cameras in different spectral regions.
The natural horizontal lines in the spectrum come from defects of the spectrograph slit.
These defects are caused by dust particles on the slit of the spectrograph
(DL - dark lines - less intensive) and by holes in the sharp edges of the slit
(bright lines - more intensive).
One should try to adjust the CCD camera in the focal plane of the spectrograph to
align the edge of the image (the X axis) parallel to the horizontal sharp lines
appearing in the spectrum.
In any case, some inaccuracy (even a fraction of pixel) remains.
This introduces problems in the next steps of reduction and also if one tries to calculate
continua on the left and right side of a spectral profile using one row of the spectrum.
To make the horizontal lines parallel to the edge of the image we used our procedure
which allows us to shift the columns of the CCD image in the Y direction gradually with
an arbitrary predefined accuracy without shifting of any part of the spectrum in the X direction.
Re-binning and shifting of every particular column of the image in the Y direction with an
accuracy of 1/100 of a pixel was performed in this particular reduction.
As a consequence of our approach several incomplete rows at the top or at the bottom
of the image had to be cut away.
This didn't affect the next steps of the reduction, because only pure spectra between
the two WL wires were finally used for calculations of spectral characteristics.
The shifts were applied to both the mean flat-field frame
(see the inclined WL and DL in Figs. 1
and 2) are artificial and/or natural.
The artificial horizontal lines (WL) are images of wires placed on the spectrograph
slit to adjust spectra taken by different CCD cameras in different spectral regions.
The natural horizontal lines in the spectrum come from defects of the spectrograph slit.
These defects are caused by dust particles on the slit of the spectrograph
(DL - dark lines - less intensive) and by holes in the sharp edges of the slit
(bright lines - more intensive).
One should try to adjust the CCD camera in the focal plane of the spectrograph to
align the edge of the image (the X axis) parallel to the horizontal sharp lines
appearing in the spectrum.
In any case, some inaccuracy (even a fraction of pixel) remains.
This introduces problems in the next steps of reduction and also if one tries to calculate
continua on the left and right side of a spectral profile using one row of the spectrum.
To make the horizontal lines parallel to the edge of the image we used our procedure
which allows us to shift the columns of the CCD image in the Y direction gradually with
an arbitrary predefined accuracy without shifting of any part of the spectrum in the X direction.
Re-binning and shifting of every particular column of the image in the Y direction with an
accuracy of 1/100 of a pixel was performed in this particular reduction.
As a consequence of our approach several incomplete rows at the top or at the bottom
of the image had to be cut away.
This didn't affect the next steps of the reduction, because only pure spectra between
the two WL wires were finally used for calculations of spectral characteristics.
The shifts were applied to both the mean flat-field frame
 and
the spectrum S1.
and
the spectrum S1.
The spectral lines in both the spectrum S and the mean flat-field frame
 exhibit curvature and inclination along the slit (along Y).
The curvature is caused by the spectrograph design and the line inclination
appears due to an inaccuracy in the adjustment of the parallel between the
vertical edges of the CCD camera and the spectrum.
exhibit curvature and inclination along the slit (along Y).
The curvature is caused by the spectrograph design and the line inclination
appears due to an inaccuracy in the adjustment of the parallel between the
vertical edges of the CCD camera and the spectrum.
The correction of spectral line stretching and inclination is essential for the next
steps of flat-fielding.
To erase the spectral line from the
 the smoothing also runs in the Y direction in the image.
If the spectral line in the
the smoothing also runs in the Y direction in the image.
If the spectral line in the
 is not strictly vertical, i.e. parallel with
the Y edge of the image, the process will not work correctly, as we will see later.
The best procedure to estimate line "stretching'' is to utilize a terrestrial
line if it is available in the spectrum. Such a line has a well defined and stable
centre.
The positions of the centres determined for every scan directly reflect the curvatures
and inclination of the spectral lines in the particular spectral region.
But often there are no terrestrial lines available in the spectrum or the terrestrial
lines are very weak, e.g. as in our case.
Here we used the smoothed observed line itself derived from the mean flat-field frame
is not strictly vertical, i.e. parallel with
the Y edge of the image, the process will not work correctly, as we will see later.
The best procedure to estimate line "stretching'' is to utilize a terrestrial
line if it is available in the spectrum. Such a line has a well defined and stable
centre.
The positions of the centres determined for every scan directly reflect the curvatures
and inclination of the spectral lines in the particular spectral region.
But often there are no terrestrial lines available in the spectrum or the terrestrial
lines are very weak, e.g. as in our case.
Here we used the smoothed observed line itself derived from the mean flat-field frame
 as the source of the required information.
Again, the vector of the positions of the centres of the particular line profile
(row) gave us information about the curvature and inclination of the spectral lines
along the slit.
Such a vector is given in Fig. 4b.
The vector of the positions of the centres was approximated by a polynomial approximation
of the second order in this case (thick line in Fig. 4b). The resulting polynomial approximation was finally used for shifts of every particular scan
(row) in the X direction to make the spectral lines parallel to the Y edges of the image.
An identical polynomial approximation for shift was applied to both the mean flat-field
frame
as the source of the required information.
Again, the vector of the positions of the centres of the particular line profile
(row) gave us information about the curvature and inclination of the spectral lines
along the slit.
Such a vector is given in Fig. 4b.
The vector of the positions of the centres was approximated by a polynomial approximation
of the second order in this case (thick line in Fig. 4b). The resulting polynomial approximation was finally used for shifts of every particular scan
(row) in the X direction to make the spectral lines parallel to the Y edges of the image.
An identical polynomial approximation for shift was applied to both the mean flat-field
frame
 and the spectrum S1.
This again, similar to the previous step, required several incomplete columns on the left
and right of the image to be cut away.
The prepared spectrum S2 and the mean flat-field frame
and the spectrum S1.
This again, similar to the previous step, required several incomplete columns on the left
and right of the image to be cut away.
The prepared spectrum S2 and the mean flat-field frame
 after
all steps of the reduction mentioned above are shown in Fig. 5.
The spectrum S2 will be used in the extended and precise reduction.
after
all steps of the reduction mentioned above are shown in Fig. 5.
The spectrum S2 will be used in the extended and precise reduction.
 |
Figure 5:
The prepared spectrum S2 a) and the prepared mean flat-field frame
 b) after corrections for segment-flat M6, for X inclination
and for stretching and Y inclination of the spectral lines.
The grey-scale bars give relative intensities expressed in ADU.
The rectangular box marked the area where the standard deviations were calculated
(see Sect. 5).
b) after corrections for segment-flat M6, for X inclination
and for stretching and Y inclination of the spectral lines.
The grey-scale bars give relative intensities expressed in ADU.
The rectangular box marked the area where the standard deviations were calculated
(see Sect. 5). |
 |
Figure 6:
a) The "hard'' flat-field matrix M1,4,5 composed of the pixel-flat, the slit-flat and the camera-flat; b) The "soft'' flat-field matrix M2,3 composed of
the illumination-flat and shutter-flat; c) The slit-flat matrix M5;
d) The flat-field matrix M1,4 composed of the pixel-flat
and camera-flat. The grey-scale bars give relative
intensities normalized to 1.0. |
The flat-field matrix
M1,2,3,4,5 will be defined in our case formally with an
equation similar to the Eq. (5) which defined the ith particular flat-field
matrix Mi but our resulting matrix M will be composed of five flat-fields and
it will still contain the spectral lines.
These lines must be erased from the matrix M to get the flat-field frame(s) commonly used
for flat-fielding. The flat-field matrix equation reads:
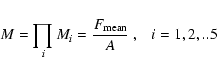 |
(10) |
where M is the flat-field matrix composed of the five individual flat-field matrices
and of spectral lines, A is the average pixel value used for normalization and
 represents the mean-flat field frame defined by Eq. (9).
Different
represents the mean-flat field frame defined by Eq. (9).
Different
 were used for different approaches of the reduction.
The
were used for different approaches of the reduction.
The
 created from the raw mean flat-field (Fig. 2) and corrected for
segment flat M6 was used in the simple reduction.
The manipulated
created from the raw mean flat-field (Fig. 2) and corrected for
segment flat M6 was used in the simple reduction.
The manipulated
 shown in Fig. 5b was used in the
extended and precise reduction.
shown in Fig. 5b was used in the
extended and precise reduction.
Equation (10) is calculated in two steps:
-
The flat-field matrix composed of the illumination-flat M2, of the shutter-flat M3 and of spectral lines is derived from
 .
This we call a "soft'', part of the flat-field matrix M due to its smooth character;
.
This we call a "soft'', part of the flat-field matrix M due to its smooth character;
-
The flat-field matrix composed of the pixel-flat M1, the camera-flat M4,
and the slit-flat M5 is retrieved from
 .
This we call a "hard'' part of the flat-field matrix M due to its sharp "spiky'' character.
.
This we call a "hard'' part of the flat-field matrix M due to its sharp "spiky'' character.
The procedure smooths the image with a rectangular box (window) in both directions.
Then additional smoothing of scans (rows) in the X direction by a least squares function
spline is done and finally, for each column of the image the linear interpolation along
the Y direction between the scans of the predefined box (window) is carried out.
We used a window of 9 pixels width.
Dividing the mean-flat field frame
 by the "soft'' part of the flat-field
matrix M we derived the "hard'' part of the flat-field matrix M.
This is shown in Fig. 6a.
Then the spectral lines are eliminated from the "soft'' part of the
flat-field matrix M dividing this part by "mean scan''.
It is constructed as an average of all rows of the image.
From this last step it is clear why the spectral lines must be parallel to the Y edge of the image.
If it is not the case, some residual intensities in every row of the image will remain.
This incorrect resulting "soft'' flat-field matrix M2,3 is shown in
Fig. 4a.
The correct "soft'' M2,3 is shown in Fig. 6b.
by the "soft'' part of the flat-field
matrix M we derived the "hard'' part of the flat-field matrix M.
This is shown in Fig. 6a.
Then the spectral lines are eliminated from the "soft'' part of the
flat-field matrix M dividing this part by "mean scan''.
It is constructed as an average of all rows of the image.
From this last step it is clear why the spectral lines must be parallel to the Y edge of the image.
If it is not the case, some residual intensities in every row of the image will remain.
This incorrect resulting "soft'' flat-field matrix M2,3 is shown in
Fig. 4a.
The correct "soft'' M2,3 is shown in Fig. 6b.
In this section, we will first analyze the main reason for the temporal changes of the
flat-field conditions, the spectrograph drift.
Then we will show that the time dependent parts of the flat-field matrix M are the
slit-flat M5, and illumination-flat M2.
Finally we will demonstrate how to solve post factum the problem of the temporal changes
of the flat-field conditions.
We split the "hard'' part of the flat-field matrix M into two components, the slit-flat M5 and the flat-field matrix M1,4 composed of pixel-flat and camera-flat.
Drift of the spectrograph
Spectrographs with high resolution and dispersion exhibit drift of the spectral
lines and changes of the dispersion, e.g. due to thermal bending of mechanical
components, like support structures of the slit basement, the collimating and focusing
mirrors and the grating itself.
It has to be taken into account that asymmetric heating of the
solar towers occurs in the daytime with sunshine coming in the morning
from the east and in the afternoon from the west.
This can be measured with terrestrial spectral lines (e.g. of oxygen), laboratory
molecular lines (e.g. of iodine) or laser reference lines. A detailed investigation made by Thiele (1982) showed for the solar
spectrograph at Locarno drifts up to 0.5 pm per hour.
Such drifts can still be determined using terrestrial oxygen lines.
There was a high correlation of the drifts and changes of their sign with
the recorded temperature in the environment in the data of Thiele.
Very stable lasers used to control a Fourier Spectrometer (Brault 1979)
allowed the determination of even shifts of the oxygen lines of the order of 0.01 pm
within a day due to wind in the Earth's atmosphere (Balthasar et al. 1982).
For the VTT no published data about the drift of its spectrograph exist.
Within the investigation performed in 1988 one of the authors (H.W.) determined
drifts using terrestrial oxygen lines 6302.005 Å and 6302.771 Å.
He found drifts that ranged from 0.015 pm within a minute up to 0.3 pm within an
hour in August 1988.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{MS2154f12.eps}
\end{figure}](/articles/aa/full/2002/42/aa2154/Timg51.gif) |
Figure 7:
The "slit-vector'' which represents the average of all columns of
the flat-field matrix M1,4,5 shown in Fig. 6a. |
We also found the drift of the spectrum in the focal plane of the spectrograph of VTT in both directions in a data set observed in 1996 using different CCD cameras.
Again the terrestrial lines of the oxygen molecule 6302.005 Å and 6302.771 Å were used for determination of the drift in wavelength direction.
The wires (WL) in the images were used as tracers for determination of the drift in
spatial direction.
Values of 1.06 pm (1.3 pixel) per hour and 0.26 arcsec (1.5 pixel) per hour
were found for the X and Y directions, respectively.
In addition we have found that the drift was not linear.
It was steepest in the morning and gradually decreased in the middle of the day.
The analysis of the drift made with the data used in this work shows that the drift
in the spatial direction (the WL wires were used for tracking) was 1.7 pixel per hour
that corresponds to 0.21 arcsec. It is in agreement with the previous results.
Time dependent parts of the flat-field matrix M
As we have documented above the spectrograph drift moves the image (spectrum) in the
focal plane of the spectrograph in both the X and Y directions.
This will affect only two components of the whole flat-field matrix M, namely the
illumination-flat M2 and the slit-flat M5, because the other three M1,3,4, i.e. the pixel-flat, the shutter-flat and the camera-flat
are closely connected to the CCD camera body.
The intensity errors caused by the movement of the illumination-flat M2 are
negligible because its gradient is very small across the camera field
(see Fig. 6b).
Thus a shift of even several pixels does not match any measurable effect in intensity
changes.
We separated the M2 (together with the shutter-flat M3) directly in the
flat-fielding procedure as the "soft'' part of the flat-field matrix M.
The movement of the slit-flat M5 is much more important.
This flat-field is caused by dust and defects of the spectrograph slit.
These show rapid changes of the intensity across the camera field in the Y direction and they are seen as the horizontal white and black lines and stripes
described in Fig. 2 and mentioned above many times.
The movement of the slit-flat M5 acts in both the X and Y direction in
the spectrum.
The movement of the slit-flat M5 in the X direction is not important.
The horizontal lines do not significantly change their intensities in the X direction
because the inclination of the image was corrected in the previous step of the
reduction (cf. Sect. 4.4.1).
But movement of the slit-flat M5 in the Y direction by even a fraction of a
pixel changes dramatically the whole "hard'' flat-field matrix M1,4,5 which
then does not match the conditions valid for the observed spectrum S2.
To solve this problem, one has to separate the slit-flat M5 from the
"hard'' part of the flat-field matrix M1,4,5 (Fig. 6a),
to be able to shift only the slit-flat M5 in the Y direction, to fit the
particular spectrum S2 well.
Separation of the slit-flat M5
We benefited from the fact that only the slit-flat M5 is uniform in the
X direction.
This is a direct consequence of the imaging of the slit on the focal plane of the
spectrograph.
Thus, the vector made as an average of all columns of the "hard'' flat-field M1,4,5 will mainly represent the fluctuations of the slit-flat M5in the Y direction because the other two components, the pixel-flat M1 and
the camera-flat M4, are randomly distributed across the CCD image and they
will not contribute systematically to the averaged vector.
We denoted this vector the "slit-vector'' (see Fig. 7).
We created a new array of the same dimensions as the spectrum S2 and the
"slit-vector'' was replicated in all columns of the created array.
Thus, this new array represents the pure slit-flat M5 (see Fig. 6c).
Obtaining the pure slit-flat M5 makes it possible to extract the pixel-flat
and the camera-flat M1,4 dividing the "hard'' flat-field matrix M1,4,5
by the pure slit-flat M5. The resulting M1,4 is shown in Fig. 6d.
 |
Figure 8:
a) The spectrum R2 as the resultant of the
extended reduction made according to Eq. (12). The symbols V and H denote the sharp intensity spikes resulting from incorrect fitting of
the strips and lines caused by dust and defects on the spectrograph slit and
by the artificial wires seen
in the prepared spectrum S2; b) The spectrum R3 as the
resultant of the
precise reduction made according to the Eq. (13).
The grey-scale bars give relative
intensities expressed in ADU. |
At the beginning of Sect. 4 we defined the simple, extended and
precise reductions. According to those definitions, we can rewrite
Eq. (3) valid for flat-fielding in the three following forms:
Simple flat-fielding
This flat-fielding was done with the flat-field matrix
M1,2,3,4,5 which was
constructed according to Eq. (10) directly from the raw mean flat-field
frame
 (cf. Fig. 2) corrected only for the segment-flat M6.
So the simply reduced spectrum R1 is defined by the equation:
(cf. Fig. 2) corrected only for the segment-flat M6.
So the simply reduced spectrum R1 is defined by the equation:
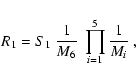 |
(11) |
where the spectrum S1 defined by Eq. (6) was corrected for background
and different sensitivities of the segments of the CCD chip only.
The simple spectral characteristics were calculated using this reduced
spectrum R1.
Extended flat-fielding
In the extended approach of the flat-fielding we omitted only step 4.5 of the
reduction, i.e. the appropriate shift of the slit-flat matrix M5.
The consequence is that the flat-field matrix M exhibits a shift comparing to the
spectrum S2.
Thus, the equation used for extended flat-fielding is formally identical
to the previous one:
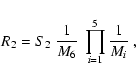 |
(12) |
but the spectrum S2 represents here the manipulated prepared spectrum S2
shown in Fig. 5a, and the flat-field matrix
M1,2,3,4,5was retrieved from the prepared mean flat-field frame
 shown in
Fig. 5b.
It means that S2 as well as
shown in
Fig. 5b.
It means that S2 as well as
 were corrected not only for
background and different sensitivities of the segments of the CCD chip but also for
the X inclination of the image and for stretching and the Y inclination of the
spectral lines.
The resulting R2 is shown in Fig. 8a.
The extended spectral characteristics
were calculated using this reduced spectrum R2.
There are still sharp horizontal lines and stripes in R2.
This is due to temporal changes of the flat-field conditions mainly caused by the drift
of the spectrograph.
Thus, the mean flat-field frame
were corrected not only for
background and different sensitivities of the segments of the CCD chip but also for
the X inclination of the image and for stretching and the Y inclination of the
spectral lines.
The resulting R2 is shown in Fig. 8a.
The extended spectral characteristics
were calculated using this reduced spectrum R2.
There are still sharp horizontal lines and stripes in R2.
This is due to temporal changes of the flat-field conditions mainly caused by the drift
of the spectrograph.
Thus, the mean flat-field frame
 constructed from the flat-field source
frames F taken at the beginning of the observing run does not perfectly match the
flat-field conditions valid for the moment of the particular spectrum P registration.
The resulting flat-field matrix
M1,2,3,4,5 is slightly shifted in both directions
comparing to S2.
So, some defects are enhanced instead of suppressed in R2.
constructed from the flat-field source
frames F taken at the beginning of the observing run does not perfectly match the
flat-field conditions valid for the moment of the particular spectrum P registration.
The resulting flat-field matrix
M1,2,3,4,5 is slightly shifted in both directions
comparing to S2.
So, some defects are enhanced instead of suppressed in R2.
-
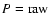 spectrum,
spectrum,
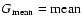 background,
R1= "simple'' spectrum,
R2= "extended'' spectrum,
R3= "precise'' spectrum.
background,
R1= "simple'' spectrum,
R2= "extended'' spectrum,
R3= "precise'' spectrum.
Precise flat-fielding
To avoid the consequences mentioned above the precise flat-fielding differs in
the following way:
we compared the "Y'' coordinates of the WL wires in the slit-flat M5(Fig. 6c) and in the prepared spectrum S2 (Fig. 5a)
looking for the highest correlation.
The difference and direction in which the slit-flat M5 must be shifted in the
Y direction to fit the prepared spectrum S2 was found.
For the shift of the slit-flat M5 we used our procedure in which the image
is re-binned 100 times up to get a shift accuracy of 1/100 of pixel.
This was done step by step, along the X direction to avoid the production of an extremely
large array. It means that every particular column of the image was re-binned 100 times,
shifted appropriately and re-binned back.
The Eq. (12) will be modified in this case to equation:
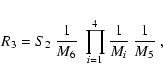 |
(13) |
where the S2, M6 and Mi are identical to those which take place
in Eq. (12) and M5 denotes the new shifted slit-flat M5.
The precise spectrum R3 reduced according to Eq. (13) is represented
in Fig. 8b.
We need to keep the positions of the artificial wires WL for adjustment between the
two CCD images taken with different CCD cameras in different spectral regions.
Therefore, just before dividing the prepared spectrum S2 by the flat-field matrices,
the central rows of the artificial wires WL in the flat-field matrices were replaced by
rows of mean intensity.
After dividing the spectrum by the flat-field matrices the two horizontal central WL wires
appeared back in identical positions in the reduced spectrum R3 because they had not
been removed from the prepared spectrum S2.
-
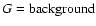 ,
,
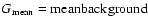 ,
,
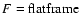 ,
,
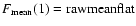 ,
,
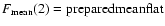 ,
M1,4,5= "hard'' part of M,
M2,3= "soft'' part of M,
,
M1,4,5= "hard'' part of M,
M2,3= "soft'' part of M,
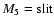 -flat,
-flat,
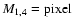 and camera flat.
and camera flat.


Up: Precise reduction of solar
Copyright ESO 2002
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{MS2154f2.eps}
\end{figure}](/articles/aa/full/2002/42/aa2154/Timg32.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{MS2154f3.eps}
\end{figure}](/articles/aa/full/2002/42/aa2154/Timg34.gif)
![]() .
Namely, the
.
Namely, the
![]() for the first (sandwiching) method will be defined
as:
for the first (sandwiching) method will be defined
as:
![]() have some limitations.
Usually, one tries to observe the long series during the best seeing conditions,
keeping the spectrograph slit in the same position of the solar disk or scanning
within small areas.
Thus, the average of many raw spectra P still exhibits shifted patterns which remain
from the real Doppler velocity shifts of a particular part of every particular
raw spectrum P.
This results in non-uniform
have some limitations.
Usually, one tries to observe the long series during the best seeing conditions,
keeping the spectrograph slit in the same position of the solar disk or scanning
within small areas.
Thus, the average of many raw spectra P still exhibits shifted patterns which remain
from the real Doppler velocity shifts of a particular part of every particular
raw spectrum P.
This results in non-uniform
![]() in the case of the first method.
The second method with the de-focused telescope tends to optically disturb the spectrum
giving rise to lateral displacement of the location of the spectral line(s) in the
image plane in the camera and changes the fixed pattern, particularly the variations
due to fringing and illumination.
A similar displacement of the spectral lines could appear when one moves the telescope,
if the scanned area at the solar disc is very large.
This smears the spectral line due to averaging of shifted lines caused by real
differential rotation of the Sun.
in the case of the first method.
The second method with the de-focused telescope tends to optically disturb the spectrum
giving rise to lateral displacement of the location of the spectral line(s) in the
image plane in the camera and changes the fixed pattern, particularly the variations
due to fringing and illumination.
A similar displacement of the spectral lines could appear when one moves the telescope,
if the scanned area at the solar disc is very large.
This smears the spectral line due to averaging of shifted lines caused by real
differential rotation of the Sun.
![]() .
The quick movement of the telescope was kept very near to the disc centre in a quiet
region to minimize the mentioned above displacement effects in every particular
flat-field source frame F.
The final
.
The quick movement of the telescope was kept very near to the disc centre in a quiet
region to minimize the mentioned above displacement effects in every particular
flat-field source frame F.
The final
![]() was an average of 40 particular flat-field source frames Ffrom which
was an average of 40 particular flat-field source frames Ffrom which
![]() had previously been subtracted.
The mean flat-field frame
had previously been subtracted.
The mean flat-field frame
![]() is given in Fig. 2 with a description
of the most important features in the spectrum. Identical features also appear in
the raw spectrum P shown in Fig. 1.
The
is given in Fig. 2 with a description
of the most important features in the spectrum. Identical features also appear in
the raw spectrum P shown in Fig. 1.
The
![]() contains all six flat-fields Mi mentioned in Sect. 2,
and also the spectral lines as a consequence of the facts discussed in the beginning
of this section.
In the following sections we show how to retrieve the particular Mi from
the mean flat-field frame
contains all six flat-fields Mi mentioned in Sect. 2,
and also the spectral lines as a consequence of the facts discussed in the beginning
of this section.
In the following sections we show how to retrieve the particular Mi from
the mean flat-field frame
![]() .
.
![]() 0.1% for the intensity range of 400-3200 ADU.
Obtaining the segment-flat M6, it was possible to correct the mean flat-field
frame
0.1% for the intensity range of 400-3200 ADU.
Obtaining the segment-flat M6, it was possible to correct the mean flat-field
frame
![]() by dividing it by M6.
Logically, the spectrum S was also corrected in the same way at this stage of the
reduction process.
We will name this improved spectrum S1.
It will be used in the simple reduction approach.
by dividing it by M6.
Logically, the spectrum S was also corrected in the same way at this stage of the
reduction process.
We will name this improved spectrum S1.
It will be used in the simple reduction approach.
![]() even when the spectral lines were presented.
This is not the case in the other flat-field matrices.
The spectral lines constrain the flat-field matrices and we must erase them from
the
even when the spectral lines were presented.
This is not the case in the other flat-field matrices.
The spectral lines constrain the flat-field matrices and we must erase them from
the
![]() .
The smoothing processes used for retrieving the flat-field matrix M are applied to
spectra in both the X and Y directions in the image.
To run them correctly it is necessary to have the mean flat-field frame
.
The smoothing processes used for retrieving the flat-field matrix M are applied to
spectra in both the X and Y directions in the image.
To run them correctly it is necessary to have the mean flat-field frame
![]() (as well as the spectrum S1) parallel to both edges of the CCD camera.
(as well as the spectrum S1) parallel to both edges of the CCD camera.
![]() the smoothing also runs in the Y direction in the image.
If the spectral line in the
the smoothing also runs in the Y direction in the image.
If the spectral line in the
![]() is not strictly vertical, i.e. parallel with
the Y edge of the image, the process will not work correctly, as we will see later.
The best procedure to estimate line "stretching'' is to utilize a terrestrial
line if it is available in the spectrum. Such a line has a well defined and stable
centre.
The positions of the centres determined for every scan directly reflect the curvatures
and inclination of the spectral lines in the particular spectral region.
But often there are no terrestrial lines available in the spectrum or the terrestrial
lines are very weak, e.g. as in our case.
Here we used the smoothed observed line itself derived from the mean flat-field frame
is not strictly vertical, i.e. parallel with
the Y edge of the image, the process will not work correctly, as we will see later.
The best procedure to estimate line "stretching'' is to utilize a terrestrial
line if it is available in the spectrum. Such a line has a well defined and stable
centre.
The positions of the centres determined for every scan directly reflect the curvatures
and inclination of the spectral lines in the particular spectral region.
But often there are no terrestrial lines available in the spectrum or the terrestrial
lines are very weak, e.g. as in our case.
Here we used the smoothed observed line itself derived from the mean flat-field frame
![]() as the source of the required information.
Again, the vector of the positions of the centres of the particular line profile
(row) gave us information about the curvature and inclination of the spectral lines
along the slit.
Such a vector is given in Fig. 4b.
The vector of the positions of the centres was approximated by a polynomial approximation
of the second order in this case (thick line in Fig. 4b). The resulting polynomial approximation was finally used for shifts of every particular scan
(row) in the X direction to make the spectral lines parallel to the Y edges of the image.
An identical polynomial approximation for shift was applied to both the mean flat-field
frame
as the source of the required information.
Again, the vector of the positions of the centres of the particular line profile
(row) gave us information about the curvature and inclination of the spectral lines
along the slit.
Such a vector is given in Fig. 4b.
The vector of the positions of the centres was approximated by a polynomial approximation
of the second order in this case (thick line in Fig. 4b). The resulting polynomial approximation was finally used for shifts of every particular scan
(row) in the X direction to make the spectral lines parallel to the Y edges of the image.
An identical polynomial approximation for shift was applied to both the mean flat-field
frame
![]() and the spectrum S1.
This again, similar to the previous step, required several incomplete columns on the left
and right of the image to be cut away.
The prepared spectrum S2 and the mean flat-field frame
and the spectrum S1.
This again, similar to the previous step, required several incomplete columns on the left
and right of the image to be cut away.
The prepared spectrum S2 and the mean flat-field frame
![]() after
all steps of the reduction mentioned above are shown in Fig. 5.
The spectrum S2 will be used in the extended and precise reduction.
after
all steps of the reduction mentioned above are shown in Fig. 5.
The spectrum S2 will be used in the extended and precise reduction.
![]() by the "soft'' part of the flat-field
matrix M we derived the "hard'' part of the flat-field matrix M.
This is shown in Fig. 6a.
Then the spectral lines are eliminated from the "soft'' part of the
flat-field matrix M dividing this part by "mean scan''.
It is constructed as an average of all rows of the image.
From this last step it is clear why the spectral lines must be parallel to the Y edge of the image.
If it is not the case, some residual intensities in every row of the image will remain.
This incorrect resulting "soft'' flat-field matrix M2,3 is shown in
Fig. 4a.
The correct "soft'' M2,3 is shown in Fig. 6b.
by the "soft'' part of the flat-field
matrix M we derived the "hard'' part of the flat-field matrix M.
This is shown in Fig. 6a.
Then the spectral lines are eliminated from the "soft'' part of the
flat-field matrix M dividing this part by "mean scan''.
It is constructed as an average of all rows of the image.
From this last step it is clear why the spectral lines must be parallel to the Y edge of the image.
If it is not the case, some residual intensities in every row of the image will remain.
This incorrect resulting "soft'' flat-field matrix M2,3 is shown in
Fig. 4a.
The correct "soft'' M2,3 is shown in Fig. 6b.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{MS2154f12.eps}
\end{figure}](/articles/aa/full/2002/42/aa2154/Timg51.gif)
