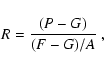2 Basic definitions

   

Table 1: Main characteristics of KIS XEDAR CCD camera.

(1)	number of pixels: 2048*2048
(2)	mean pixel distance: 14 microns
(3)	vendor of the camera: XEDAR CORP., USA
(4)	chip used: Thomson TH/899M
(5)	sensitivity range: 400 nm to 1100 nm
(6)	window type: glass, wedge-shaped
(7)	interference pattern: not detectable
(8)	cooling: two stage cooling, at -10 deg C
(9)	controller: SUN workstation
(10)	digital precision: 12 bits

The fundamental task of photometric spectrum reduction is to "clean'' the observed raw spectrum without affecting the true spectral intensity information included in the image and to keep the S/N ratio as high as possible. It means that one must accurately account for the changes of intensities imposed by the imaging system. Under the term "imaging system'' we consider here the optical system of the instrument as well as the CCD camera itself. The process by which a CCD image is adequately recovered is known as flat-fielding. Basically, the flat-field is a correction for the variation in response of the pixels in the image. If one took an image of a uniformly illuminated surface, then the ideal CCD image would show it as having constant counts in every pixel. The term "flat-field correction'' then refers to the process of correction of the CCD image so that it acts as if it has uniform response everywhere. A flat frame is the 2D matrix used to make this correction. The basic flat-field correction can be described by the following equation:

$$R = \frac{(P-G)}{(F-G)/A}~,$$ (1)

where R is the resulting reduced spectrum (image), P is the observed particular raw spectrum, F is the flat-field source frame, A is the average pixel value of the corrected flat-field source frame used for normalization, i.e. to scale the flat-field source frame to a mean intensity of 1.0 and

 

G = D+B+L  (2)

is the background composed of dark current D, bias B and scattered light L.

Although, the Eq. (1) seems to be very simple, doing flats is certainly complicated. Every term of the right side of the Eq. (1) exhibits difficulties in flat-fielding of real solar spectra observed with a real CCD camera. Generally, the background G can change during the observing run, the bias B is not constant with time or temperature and the scattered light Lcould change with a different setup of the instrument. The flat-field is used not only to take care of non-uniform response across the surface of the chip, but it is also used to take care of defects in the optical system that result in non-uniform illumination of the chip. These could be reflections, dust, shutter effect and any other non-uniformities, whatever their source. Therefore the flat-field is absolutely essential for precise photometric analysis of CCD spectra. Because there are many different factors that cause response variations, there are actually many different kinds of flat-field source frames to create and apply to an image. Therefore, a more general relation for n flat-fields takes the following form:

$$R = {S} \prod_{i=1}^n \frac{1}{M_i}~,$$ (3)

where

 

S = P-G (4)

is the spectrum from which the background G was subtracted and

$$M_i = \frac{F_i-G}{A_i}~, ~~~i=1,2,...{\it n},$$ (5)

where F_i are flat-field source frames used for every ith particular effect of non-uniform response of the chip or non-uniform illumination of the chip. The common types of flat-fields we will deal with in this paper are:
$M_{\rm 1}$ - "pixel-flat'': the flat-field used for correction of the non-uniform sensitivity of the pixels across the chip; This is generally wavelength dependent. But in the case of high spectral resolution CCD spectra only a very short range in wavelength ($\sim$3 Å) is taken on the chip, so the effect is negligible in our case;
$M_{\rm 2}$ - "illumination-flat'': the flat-field which will correct large gliding changes of the intensity across the chip caused by optical vignetting, dust particles imaged out of the focus, etc.
$M_{\rm 3}$ - "shutter-flat'': flat-field used to suppress the non-uniformity of the exposure caused by the finite travel time of the shutter across the field of view;
$M_{\rm 4}$ - "camera-flat'': flat-field for correction of CCD camera effects, for example interference at the glass window of the CCD camera or dust lying on the CCD camera window. Generally, the interference is wavelength dependent and also the introducing of any optical filter on the camera window changes this flat-field matrix;
$M_{\rm 5}$ - "slit-flat'': flat-field for corrections of the non-uniform illumination of the chip caused by the dust lying on the spectrograph slit and/or by imperfection of the slit and/or by non-parallel edges of the slit;
$M_{\rm 6}$ - "segment-flat'': flat-field for corrections of the different sensitivity of sub-chips to light. (The CCD detector we used is composed of four independent segments).

Sometimes several types of flat-fields must be grouped into one flat-field matrix M for correction of several effects together. We will show later that in the case of large solar spectra all the flat-fields must be derived from one flat-field frame.