It is instructive to compare the projected XMM-Newton temperature profile
of A1413 with the composite profiles found for larger cluster samples.
The most extensive samples come from ASCA and BeppoSAX
data; these are, in order of publication: Markevitch et al. (1998;
MFSV98), White (2000; W00) Irwin & Bregman (2000; IB00) and De Grandi
& Molendi (2002; DM02). The MFSV98 ASCA-derived profile is
sharply decreasing, such that for a typical ![]() cluster the
temperature drop is characterised by a polytropic index of 1.2-1.3.
W00 finds that
cluster the
temperature drop is characterised by a polytropic index of 1.2-1.3.
W00 finds that ![]() of the cluster profiles in his ASCA
sample are consistent with isothermality at the
of the cluster profiles in his ASCA
sample are consistent with isothermality at the ![]() -level. The IB00 BeppoSAX-derived profile extends only out to
-level. The IB00 BeppoSAX-derived profile extends only out to ![]() 0.3
r200 and is flat or even slightly increasing. In contrast, the
overall DM02 profile, from a larger sample of BeppoSAX
observations,
is characterised by an isothermal core extending to
0.3
r200 and is flat or even slightly increasing. In contrast, the
overall DM02 profile, from a larger sample of BeppoSAX
observations,
is characterised by an isothermal core extending to ![]() 0.2
r200. Their CF subsample exhibits a temperature drop of a
factor of 1.7 between
0.2
r200. Their CF subsample exhibits a temperature drop of a
factor of 1.7 between ![]() 0.2 r200 and
0.2 r200 and ![]() 0.5 r200. The non-CF
clusters exhibit a sharper temperature drop in the outer regions.
DM02 suggest that an incorrect treatment of the BeppoSAX
strongback may explain the discrepancy between their result and that
of IB00.
0.5 r200. The non-CF
clusters exhibit a sharper temperature drop in the outer regions.
DM02 suggest that an incorrect treatment of the BeppoSAX
strongback may explain the discrepancy between their result and that
of IB00.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{MS2734f12.ps}
\end{figure}](/articles/aa/full/2002/41/aa2734/Timg213.gif) |
Figure 12:
The projected scaled temperature profile of A1413
compared to the composite CF cluster profile as obtained by De Grandi
& Molendi 2002 (dot-dash lines are joining their data
points plus or minus the |
Our data are compared to the DM02 and MFSV98 composite profiles in
Fig. 12. Although each individual data point is
(marginally) consistent with the typical region defined by these
composite profiles, there is an obvious systematic difference in
shape. The A1413 profile does not decline sharply like the composite
profile of MFSV98, or the profile of DM02 beyond ![]() 0.2 r200.
In Sect. 5.4, we show that the polytropic model gives
an acceptable fit to the data. Excluding the central bin, the
0.2 r200.
In Sect. 5.4, we show that the polytropic model gives
an acceptable fit to the data. Excluding the central bin, the
![]() value (1.07) implies an almost isothermal temperature
profile, and is not compatible with that found by MFSV98. It is very
similar to that found by DM02 for CF clusters, but DM02 reject the
polytropic model on the grounds of poorness of fit, which is not
surprising given the decline of a factor of 1.7 in the temperature of
their composite profile between 0.2 and
0.5 r200. We do not
see a similar decline, and so a polytropic model is a good fit to
these data. On the other hand, their best fit broken line model is a
poor fit to our data: we find a
value (1.07) implies an almost isothermal temperature
profile, and is not compatible with that found by MFSV98. It is very
similar to that found by DM02 for CF clusters, but DM02 reject the
polytropic model on the grounds of poorness of fit, which is not
surprising given the decline of a factor of 1.7 in the temperature of
their composite profile between 0.2 and
0.5 r200. We do not
see a similar decline, and so a polytropic model is a good fit to
these data. On the other hand, their best fit broken line model is a
poor fit to our data: we find a
![]() for their CF
best-fit, and the fit is worse for their non-CF relation (
for their CF
best-fit, and the fit is worse for their non-CF relation (
![]() ).
).
It is obvious that, given the extra radial range afforded by these
XMM-Newton data, a flat or increasing profile, such as that of W00 or IB00
extrapolated to high radii, does not describe the A1413 data either.
We emphasize again that the temperature gradient is modest: the
temperature decreases by ![]()
![]() between
0.1 r200 and
0.3(0.5) r200. Fitting the temperature profile up to
0.3 r200 (i.e., excluding the last three temperature bins, and the
inner bin) with a polytrope allows us to compare our profile directly
with that of IB00. We find
between
0.1 r200 and
0.3(0.5) r200. Fitting the temperature profile up to
0.3 r200 (i.e., excluding the last three temperature bins, and the
inner bin) with a polytrope allows us to compare our profile directly
with that of IB00. We find
![]() ,
,
![]() ,
consistent with the value derived for the full radial
range. This gradient is in agreement with the level of isothermality
found by W00 and IB00 in that radial range taking into account their
errors, as well as that found by Allen et al. (2001a) from
Chandra data below
,
consistent with the value derived for the full radial
range. This gradient is in agreement with the level of isothermality
found by W00 and IB00 in that radial range taking into account their
errors, as well as that found by Allen et al. (2001a) from
Chandra data below
![]() .
Our observation is
also consistent with other XMM-Newton observations of nearby clusters, e.g.
the slightly decreasing XMM-Newton temperature profile of Coma (
.
Our observation is
also consistent with other XMM-Newton observations of nearby clusters, e.g.
the slightly decreasing XMM-Newton temperature profile of Coma (![]() at
0.2 r200, Arnaud et al. 2001a) and the temperature
profile of A1795, measured up to
0.4 r200 and found to be flat
within
at
0.2 r200, Arnaud et al. 2001a) and the temperature
profile of A1795, measured up to
0.4 r200 and found to be flat
within ![]()
![]() beyond the CF region (
0.1 r200, Arnaud
et al. 2001b).
beyond the CF region (
0.1 r200, Arnaud
et al. 2001b).
In Sect. 8.3 we showed that the NFW form can describe the total mass profile of A1413. However a slightly better agreement in the center is obtained with a MQGSL profile, derived from higher resolution simulations.
With Chandra, it is possible to examine the central regions in
great detail, at the expense of information at large radii. At
present, it is unclear whether the NFW or MQGSL profiles provide the
better description of the mass profiles derived from Chandra
observations. Allen et al. (2001b) investigate
several forms for the mass profile of RXJ1347.5-1145, finding that
both the NFW and MQGSL provide an acceptable fit, although the NFW
profile is favoured in terms of ![]() .
Perhaps the highest
resolution examination of a cluster mass profile is that of Hydra A by
David et al. (2001), who find
.
Perhaps the highest
resolution examination of a cluster mass profile is that of Hydra A by
David et al. (2001), who find
![]() between 30 and 200 kpc, which is intermediate between the NFW and MQGSL forms.
The addition of a mass point from H
between 30 and 200 kpc, which is intermediate between the NFW and MQGSL forms.
The addition of a mass point from H![]() observations leads them
to favour the NFW profile, although the result is still consistent
with the MQGSL result.
observations leads them
to favour the NFW profile, although the result is still consistent
with the MQGSL result.
One sticking point is the value of the concentration parameter from
the NFW fit by David et al. (2001). They find c = 12,
which is 3 times that expected for a cluster of the mass of Hydra A.
Interestingly, a similar value of c was found by Arabadjis et al. (2002) from a Chandra study of EMSS 1358+6245.
On the other hand, the c parameters of Allen et al. (2001a) are
better in agreement with the theoretical predictions. At large radii
the NFW and MQGSL profiles coincide and we can compare the c value
derived from our NFW fit,
![]() for a
for a
![]() cluster, to numerical simulations. Teyssier
(2002) derived c parameters in the range 4.9-9.5 for 5 clusters in this very mass range. The average c parameter derived
by Eke et al. (1998) for hot massive clusters is
cluster, to numerical simulations. Teyssier
(2002) derived c parameters in the range 4.9-9.5 for 5 clusters in this very mass range. The average c parameter derived
by Eke et al. (1998) for hot massive clusters is ![]() .
It
must be noted that a relatively large dispersion on this parameter is
expected from numerical simulations, with a
.
It
must be noted that a relatively large dispersion on this parameter is
expected from numerical simulations, with a
![]() at a given mass (Bullock
et al. 2001). In conclusion, we emphasize the excellent
agreement in shape between the mass profile derived for A1413
and the theoretical expectations, all the more remarkable in view of
the very small statistical errors on the profile.
at a given mass (Bullock
et al. 2001). In conclusion, we emphasize the excellent
agreement in shape between the mass profile derived for A1413
and the theoretical expectations, all the more remarkable in view of
the very small statistical errors on the profile.
We now examine the normalisation of the mass profile. We will
classically define
![]() ,
the mass within a given radius
,
the mass within a given radius
![]() ,
inside which the mean mass density is
,
inside which the mean mass density is ![]() times the
critical density,
times the
critical density,
![]() at the cluster redshift. For
clusters obeying HE and self-similarity, the mass
at the cluster redshift. For
clusters obeying HE and self-similarity, the mass
![]() ,
scales with the cluster temperature and redshift as:
,
scales with the cluster temperature and redshift as:
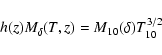 |
(23) |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{MS2734f13.eps}\par
\end{figure}](/articles/aa/full/2002/41/aa2734/Timg234.gif) |
Figure 13:
The scaled mass profile of A1413 (data
points), expressed as a function of density contrast, |
In Fig. 13 we show the scaled mass profile of A1413
defined as:
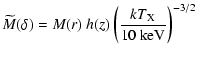 |
Both the data points and the MQGSL and polytropic model curves run
parallel to the EMN96 profile down to
![]() .
This simply
reflects the excellent agreement in shape of the A1413 profile with
numerical simulations, as outlined above. However there is a very
significant offset in normalisation:
.
This simply
reflects the excellent agreement in shape of the A1413 profile with
numerical simulations, as outlined above. However there is a very
significant offset in normalisation:
![]() ,
compared with
,
compared with
![]() from EMN96. In other words,
the predicted normalisation of the M-T relation lies
from EMN96. In other words,
the predicted normalisation of the M-T relation lies ![]()
![]() higher than the observed value, in excellent agreement with the Chandra finding of Allen et al. (2001a,
higher than the observed value, in excellent agreement with the Chandra finding of Allen et al. (2001a, ![]()
![]() at
at
![]() ).
).
Below
![]() the observed profile levels off, so that the data
points seem to converge towards the EMN96 predictions at small
the observed profile levels off, so that the data
points seem to converge towards the EMN96 predictions at small ![]() .
At
.
At
![]()
![]() ,
only
,
only ![]() lower than the EMN96 value of
lower than the EMN96 value of
![]() and actually consistent with it,
especially if we also take into account the dispersion observed in the
simulations (
and actually consistent with it,
especially if we also take into account the dispersion observed in the
simulations (![]() ). If this effect is real, this would point to a
fundamental difference of form in the total mass profile at
large radii, i.e. the real cluster dark matter density profile drops
less steeply than the canonical r-3 law. The observed
discrepancy in the normalisation of the M-T relation at high
density contrast would thus be due to a flaw in the numerical
simulations for the dark matter component.
). If this effect is real, this would point to a
fundamental difference of form in the total mass profile at
large radii, i.e. the real cluster dark matter density profile drops
less steeply than the canonical r-3 law. The observed
discrepancy in the normalisation of the M-T relation at high
density contrast would thus be due to a flaw in the numerical
simulations for the dark matter component.
However, it is more likely that this level off of the observed
profile is an artifact due to incomplete virialisation. If there is
residual kinetic energy due to infall, the HE equation applied to the
observed temperature profile would over-estimate the true mass. Such
an effect is observed in the simulations of EMN96, although its
expected magnitude is somewhat smaller that we observe, ![]()
![]() at
at
![]() on average (but a large scatter exists). A further
indication that this is the correct explanation comes from a
comparison with the polytropic temperature model. Let us assume that
the best fit MQGSL model indeed reflects the true total mass
distribution. The fact that the mass profile derived from the best
fit polytropic model closely follows this profile down to
on average (but a large scatter exists). A further
indication that this is the correct explanation comes from a
comparison with the polytropic temperature model. Let us assume that
the best fit MQGSL model indeed reflects the true total mass
distribution. The fact that the mass profile derived from the best
fit polytropic model closely follows this profile down to
![]() (see Fig. 13), indicates that this model is a true
representation of the thermodynamic state of the gas if it was in HE
up to there. The drop in temperature in the last bin (
(see Fig. 13), indicates that this model is a true
representation of the thermodynamic state of the gas if it was in HE
up to there. The drop in temperature in the last bin (
![]() ),
as compared to this model, would thus be an direct indication of
incomplete thermalisation. We also recall that there is a sudden drop
in the surface brightness profile at
),
as compared to this model, would thus be an direct indication of
incomplete thermalisation. We also recall that there is a sudden drop
in the surface brightness profile at
![]() ,
corresponding to a density contrast of 450 (computed with the MQGSL model). This further supports our interpretation: we might actually
be seeing the expected drop of the X-ray brightness beyond the edge of
the virialised (and hot) part of the cluster. Finally, incomplete
equipartition between the electrons and the ions at the border of the
cluster (Chieze et al. 1998) could also
contribute to the low (electronic) temperature observed.
,
corresponding to a density contrast of 450 (computed with the MQGSL model). This further supports our interpretation: we might actually
be seeing the expected drop of the X-ray brightness beyond the edge of
the virialised (and hot) part of the cluster. Finally, incomplete
equipartition between the electrons and the ions at the border of the
cluster (Chieze et al. 1998) could also
contribute to the low (electronic) temperature observed.
The observed scaled mass profile depends on the cosmological
model via the function h(z), used in the scaling, and the angular
distance, ![]() ,
used to convert angular radius to physical
radius. On the other hand the theoretical normalisation
,
used to convert angular radius to physical
radius. On the other hand the theoretical normalisation
![]() appears to be insensitive to cosmology. We thus
examined if a better agreement with the theoretical normalisation is
obtained for the currently most favoured
appears to be insensitive to cosmology. We thus
examined if a better agreement with the theoretical normalisation is
obtained for the currently most favoured ![]() CDM model (
CDM model (
![]() ). From Eqs. (12), (24)
and (25), the derived
). From Eqs. (12), (24)
and (25), the derived ![]() value scales as
value scales as
![]() and
and
![]() as
as
![]() ,
with
,
with
![]() .
For a
.
For a ![]() CDM model
(open circles in Fig. 13), as compared to the SCDM model (filled circles), the data points are moved down and left along
a line of slope 1/2 in the log-log plane, with
CDM model
(open circles in Fig. 13), as compared to the SCDM model (filled circles), the data points are moved down and left along
a line of slope 1/2 in the log-log plane, with ![]() multiplied by 1.137 and
multiplied by 1.137 and
![]() multiplied by 0.938. The translation is
modest and its slope is similar to the slope of the scaled mass
profile around
multiplied by 0.938. The translation is
modest and its slope is similar to the slope of the scaled mass
profile around
![]() ,
so the observed scaled mass profile
remains essentially unchanged and the agreement with the theoretical
curve is no better.
,
so the observed scaled mass profile
remains essentially unchanged and the agreement with the theoretical
curve is no better.
In summary the good agreement between the mass profile shape and the
numerical simulations, measured for the first time in the whole
virialised part of the cluster, suggest that the modelling of the Dark
Matter component is correct. However, the offset in the normalisation
of the M-T relation suggests that some physics is lacking in the
modeling of the gas. Several groups have studied the effect of non
gravitational physics, like pre-heating or cooling, on the M-Trelation (e.g. Loewenstein 2000; Bialek
et al. 1999; Tozzi & Norman 2001; Babul
et al. 2002; Thomas et al. 2002; Voit
et al. 2002; Borgani et al. 2002). A detailed comparison with numerical simulations,
which would require a statistically representative sample, is beyond
the scope of this paper. We simply note that pure pre-heating seems
to have a small effect of the M-T relation in the high temperature
range of A1413 (Loewenstein 2000; Tozzi &
Norman 2001; Babul et al. 2002) and that models
including cooling (e.g. Thomas et al. 2002) seem to be more
successful. We also emphasize that some care must be exercised when
comparing theoretical predictions with these X-ray observations. The
magnitude of the effect is not large as compared to the typical
difference of ![]()
![]() (Henry 2000) in the normalisation
derived by various groups using purely adiabatic simulations. The
dispersion of the relation, observed for both simulated (
(Henry 2000) in the normalisation
derived by various groups using purely adiabatic simulations. The
dispersion of the relation, observed for both simulated (![]()
![]() )
and real clusters, require the use of statistically well controlled
samples. Finally, a further ambiguity lies in the definition of the
temperature. The temperature profile is not exactly isothermal
(although our data suggest that the departure is small). Ideally we
should compare the data from a given instrument using the spectral
temperature estimated from simulation, after full modelling of the
plasma emission folded with the instrument response. The study of
Mathiesen & Evrard (2001) indicates that the spectral
temperature could be an underestimate of the mass-weighted temperature,
by about
)
and real clusters, require the use of statistically well controlled
samples. Finally, a further ambiguity lies in the definition of the
temperature. The temperature profile is not exactly isothermal
(although our data suggest that the departure is small). Ideally we
should compare the data from a given instrument using the spectral
temperature estimated from simulation, after full modelling of the
plasma emission folded with the instrument response. The study of
Mathiesen & Evrard (2001) indicates that the spectral
temperature could be an underestimate of the mass-weighted temperature,
by about ![]() .
Note that this effect would worsen the discrepancy
observed above. All these systematic effects have to be well
controlled, if we want to confirm the departure from the self-similar
scaling and identify the physical process responsible for it.
.
Note that this effect would worsen the discrepancy
observed above. All these systematic effects have to be well
controlled, if we want to confirm the departure from the self-similar
scaling and identify the physical process responsible for it.
From our determination of the central gas density we have calculated
a cooling radius of
![]() .
Figure 3 shows that the gas density has begun to
rise above the
.
Figure 3 shows that the gas density has begun to
rise above the ![]() -model fit at about twice this radius. This
suggests that
the main driver of the central peak in the gas distribution is the
cusp in the dark matter profile, not the CF. It is likely that the
cusp in the dark matter profile acts as a focus for the gas and the
CF. This has implications for CF mass deposition rates
-model fit at about twice this radius. This
suggests that
the main driver of the central peak in the gas distribution is the
cusp in the dark matter profile, not the CF. It is likely that the
cusp in the dark matter profile acts as a focus for the gas and the
CF. This has implications for CF mass deposition rates ![]() deduced from excesses to the
deduced from excesses to the ![]() -model, in that any application to
this cluster would result in a gross overestimate of
-model, in that any application to
this cluster would result in a gross overestimate of ![]() .
.
The ratio of the X-ray gas mass to the total gravitating mass is shown
as a function of density contrast ![]() in
Fig. 14. The
in
Fig. 14. The
![]() rises slowly with increasing
radius, up
rises slowly with increasing
radius, up
![]() .
After this point, the
.
After this point, the
![]() either
stabilises within the error if we use the total mass data points, or
continues increasing beyond if we used the best fit MQGSL total mass
profile. A conservative estimate of the gas mass fraction at
either
stabilises within the error if we use the total mass data points, or
continues increasing beyond if we used the best fit MQGSL total mass
profile. A conservative estimate of the gas mass fraction at
![]() is
is
![]() .
This shows that the hot ICM is
more extended than the dark matter distribution, as has been found
in previous studies (e.g., David et al. 1995), and is also seen in numerical simulations, and
expected from purely dynamical reasons (Chieze et al. 1997).
.
This shows that the hot ICM is
more extended than the dark matter distribution, as has been found
in previous studies (e.g., David et al. 1995), and is also seen in numerical simulations, and
expected from purely dynamical reasons (Chieze et al. 1997).
Assuming that the gas density profile follows the dark matter profile
at large radii (within a factor of 2 between r200/2 and 2r200) and a polytropic equation of state, Komatsu & Seljak
(2001) derived an analytical solution of the gas in HE in an
NFW profile. They obtained
![]() ,
or
,
or
![]() for the concentration parameter c=5.4 derived for A1413, and a X-ray outer slope of
for the concentration parameter c=5.4 derived for A1413, and a X-ray outer slope of
![]() for a typical 6.5 keV cluster (their Fig. 14). The first assumption is roughly
verified for our best fit profiles and not surprisingly, our derived
values are in fair agreement with their model, although we obtain a
slightly but significantly lower value of
for a typical 6.5 keV cluster (their Fig. 14). The first assumption is roughly
verified for our best fit profiles and not surprisingly, our derived
values are in fair agreement with their model, although we obtain a
slightly but significantly lower value of
![]() and
a slightly higher
and
a slightly higher ![]() value.
value.
The value at
![]() ,
corresponding roughly to the virialised
part of the cluster,
,
corresponding roughly to the virialised
part of the cluster,
![]() ,
can be used to calculate the
total mass
density in the Universe, following the arguments that assume that the
properties of clusters constitute a fair sample of those of the
Universe as a whole (e.g., White et al. 1993). Assuming that
the
luminous baryonic mass in galaxies in A1413 is approximately one-fifth
of the X-ray ICM mass (e.g., White et al. 1993), and
neglecting other possible sources of baryonic dark matter,
,
can be used to calculate the
total mass
density in the Universe, following the arguments that assume that the
properties of clusters constitute a fair sample of those of the
Universe as a whole (e.g., White et al. 1993). Assuming that
the
luminous baryonic mass in galaxies in A1413 is approximately one-fifth
of the X-ray ICM mass (e.g., White et al. 1993), and
neglecting other possible sources of baryonic dark matter,
![]() ,
where
,
where
![]() is the mean baryon density. For
is the mean baryon density. For
![]() (O'Meara et al. 2001, h50 is
the Hubble
constant in units of 50 km s-1 Mpc-1), we obtain
(O'Meara et al. 2001, h50 is
the Hubble
constant in units of 50 km s-1 Mpc-1), we obtain
![]() .
.
Copyright ESO 2002