The mass profile is calculated under the usual assumptions of
hydrostatic equilibrium and spherical symmetry. The integrated mass
profile can be calculated from the gas density, ![]() ,
and
temperature profiles:
,
and
temperature profiles:
If the gas density profile is
described by the KBB model (Eq. (5)), then the mass profile
is
described by:
| = | ![$\displaystyle - \frac{{k} r^2}{{G} \mu m_{\rm p}} \left[-
\frac{3 \beta_{\rm in...
...)} T(r)}{r^{2 \xi} + r_{\rm c,in}^{2 \xi}}
+ \frac{{\rm d} T}{{\rm d} r}\right]$](/articles/aa/full/2002/41/aa2734/img169.gif) |
||
| = | ![$\displaystyle - \frac{k r^2}{{\rm G} \mu m_{\rm p}} \left[-
\frac{3 \beta r T(r)}{r^2 + r_{\rm c}^2} + \frac{{\rm d} T}{{\rm d} r}\right]$](/articles/aa/full/2002/41/aa2734/img171.gif) |
(13) |
The mass profile is calculated using the Monte Carlo method of Neumann
& Böhringer (1995). The gas density profile parameters
are fixed to their best fit values. This method calculates random
temperature profiles within the bounds of the observed profile. We
calculated 10 000 such random temperature profiles, using a window size
of 150 kpc and a smoothing parameter of
![]() .
The final output is
the mean mass profile and the corresponding errors for each data point
in the input temperature profile. The errors are calculated using the
.
The final output is
the mean mass profile and the corresponding errors for each data point
in the input temperature profile. The errors are calculated using the
![]() errors in the temperature profile and the standard deviation of
the mass at any given radius. The resulting errors are calculated to
correspond to
errors in the temperature profile and the standard deviation of
the mass at any given radius. The resulting errors are calculated to
correspond to ![]() errors in the mass profile.
errors in the mass profile.
The errors on the mass profile due to the error on the density
gradient,
![]() ,
are then calculated. As the
parameters
,
are then calculated. As the
parameters
![]() ,
,
![]() ,
,
![]() and
and ![]() are correlated, this error
cannot be deduced directly from the errors on these parameters. We
used a method similar to the one described in Elbaz et al.
(1995). For each considered radius, the surface brightness
profile is fitted, considering
are correlated, this error
cannot be deduced directly from the errors on these parameters. We
used a method similar to the one described in Elbaz et al.
(1995). For each considered radius, the surface brightness
profile is fitted, considering
![]() estimated
at this radius as a free parameter, instead of
estimated
at this radius as a free parameter, instead of ![]() .
The
.
The ![]() error on this parameter is then classically derived from the
error on this parameter is then classically derived from the
![]() variation, the other parameters (normalisation,
variation, the other parameters (normalisation,
![]() ,
,
![]() and
and ![]() )
being optimised. Finally the errors due to the
density and temperature profiles (derived from the Monte-Carlo method)
are added quadratically.
)
being optimised. Finally the errors due to the
density and temperature profiles (derived from the Monte-Carlo method)
are added quadratically.
The resulting mass profile, with ![]() error bars, is plotted in
Fig. 10.
error bars, is plotted in
Fig. 10.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{MS2734f10.eps}
\end{figure}](/articles/aa/full/2002/41/aa2734/Timg175.gif) |
Figure 10:
The mass
profile of A1413 derived from XMM-Newton surface brightness and temperature
profiles. Data points: mass derived from the HE equation, using the
Monte-Carlo method with the best fit KBB model for the gas density
(Eq. (5)) and the observed temperature profile. Errors bars
are |
The temperature profile of A1413 is well determined out to ![]() 0.7
r200, and shows a gradual decline which is well described by a
polytrope of index
0.7
r200, and shows a gradual decline which is well described by a
polytrope of index
![]() beyond the CF region.
Assuming such a polytropic description, the mass profile can be
calculated analytically from the best fit gas density KBB model. The
polytropic mass profile lies well within the errors of
the Monte Carlo profile, except
for the central point due to the temperature drop observed in the
center (full line in Fig. 10). We also note that the
derived mass at large radii (r > 1.3 Mpc) lies at the lower range of
the Monte Carlo mass. This is due to the drop of temperature in the
last radial bin, the best fit temperature being below the polytropic
value.
beyond the CF region.
Assuming such a polytropic description, the mass profile can be
calculated analytically from the best fit gas density KBB model. The
polytropic mass profile lies well within the errors of
the Monte Carlo profile, except
for the central point due to the temperature drop observed in the
center (full line in Fig. 10). We also note that the
derived mass at large radii (r > 1.3 Mpc) lies at the lower range of
the Monte Carlo mass. This is due to the drop of temperature in the
last radial bin, the best fit temperature being below the polytropic
value.
In the classic approach, the gas density is described with an
isothermal ![]() -model, in which the temperature profile is assumed
to be isothermal and the gas density distribution is parameterised by
a
-model, in which the temperature profile is assumed
to be isothermal and the gas density distribution is parameterised by
a ![]() -model. In Fig. 10 (dotted line) we show the
mass profile obtained using this approach, with the
-model. In Fig. 10 (dotted line) we show the
mass profile obtained using this approach, with the ![]() -model best
fitting the outer part of the cluster and the average cluster
temperature outside the CF region,
-model best
fitting the outer part of the cluster and the average cluster
temperature outside the CF region,
![]() .
Not surprisingly, the mass
is greatly underestimated in the centre (
.
Not surprisingly, the mass
is greatly underestimated in the centre (
![]() ), where the gas
density profile is more concentrated (higher gradient) than the
extrapolated
), where the gas
density profile is more concentrated (higher gradient) than the
extrapolated ![]() -model. If we instead parameterise the gas density
using the best fit KBB model, the mass distribution towards the centre
is recovered (Fig. 10, dashed line). Beyond
-model. If we instead parameterise the gas density
using the best fit KBB model, the mass distribution towards the centre
is recovered (Fig. 10, dashed line). Beyond
![]() the mass profile is slightly steeper than that derived from the true
temperature profile, as expected from the observed
the mass profile is slightly steeper than that derived from the true
temperature profile, as expected from the observed ![]() value,
slightly larger than 1. This comparison shows that the temperature
gradient has a small but systematic effect on the derived mass
profile.
value,
slightly larger than 1. This comparison shows that the temperature
gradient has a small but systematic effect on the derived mass
profile.
The mass profile is remarkably well constrained: the ![]() error
is less than
error
is less than ![]()
![]() below 1.4 Mpc and rises to
below 1.4 Mpc and rises to ![]()
![]() at 1.8 Mpc. The temperature logarithmic gradient is much smaller than
the density logarithmic gradient (
at 1.8 Mpc. The temperature logarithmic gradient is much smaller than
the density logarithmic gradient (![]() for
for
![]() ), except in
the very outer part, where the temperature gradient is both larger and
the constraints are poorer. As a consequence (see Eq. (12)),
except in this outer region, the error on the mass profile is
dominated by the error on the gas density gradient (in the range
), except in
the very outer part, where the temperature gradient is both larger and
the constraints are poorer. As a consequence (see Eq. (12)),
except in this outer region, the error on the mass profile is
dominated by the error on the gas density gradient (in the range
![]() )
and on the average temperature (
)
and on the average temperature (![]() ). For the same
reason the mass profile is very robust versus possible systematic
errors on the temperature profile. We have shown in
Sect. 5.2 that spectral deprojection or PSF correction do
not have a significant effect on the form of the profile. One might
also ask what effect the ellipticity of the cluster might have on the
derived radial quantities. We extracted spectra in elliptical annuli
and compared the projected temperature profile with that produced
using circular annuli. All temperatures agree within the respective
errors, and so we conclude that the cluster ellipticity is also a
minor source of error.
). For the same
reason the mass profile is very robust versus possible systematic
errors on the temperature profile. We have shown in
Sect. 5.2 that spectral deprojection or PSF correction do
not have a significant effect on the form of the profile. One might
also ask what effect the ellipticity of the cluster might have on the
derived radial quantities. We extracted spectra in elliptical annuli
and compared the projected temperature profile with that produced
using circular annuli. All temperatures agree within the respective
errors, and so we conclude that the cluster ellipticity is also a
minor source of error.
Navarro et al. (1997, NFW) performed high resolution
N-body simulations which showed that the density profiles of dark
matter halos have a universal shape, regardless of halo mass and
values of cosmological parameters. The NFW profile is given by:
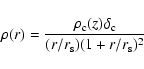 |
(14) |
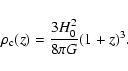 |
(15) |
![\begin{displaymath}\delta_{\rm c}= \frac{200}{3} \frac{c^3}{[{\rm ln} (1+c) - c/(1+c)]}\cdot
\end{displaymath}](/articles/aa/full/2002/41/aa2734/img190.gif) |
(16) |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{MS2734f11.eps}
\end{figure}](/articles/aa/full/2002/41/aa2734/Timg192.gif) |
Figure 11: The mass profile of A1413 fitted with the NFW profile (dotted line) and Moore et al. (1999) profile (full line). Bottom panels: residual between the data and the model. The best fit concentration parameters are c=5.4 and c=2.5 respectively (see Table 5). The radius corresponding to a density contrast of 500 is indicated by an arrow. |
| Parameter | NFW model | MQGSL model |
| c |
|
|
|
|
|
|
| r200 (kpc) | 2169 | 2221 |
|
|
|
|
|
|
8.76/9 | 6.44/9 |
The NFW density profile varies from
![]() at small radii to
at small radii to
![]() at large radii. As
we are fitting the mass profile M(r), we use the integrated mass of
the NFW profile for the fit (e.g. Suto et al. 1998):
at large radii. As
we are fitting the mass profile M(r), we use the integrated mass of
the NFW profile for the fit (e.g. Suto et al. 1998):
| M(r) | = | (17) | |
| m(x) | = | (18) |
![\begin{displaymath}\rho(r) = \frac{\rho_{\rm c}(z) \delta_{\rm c}}{(r / r_{\rm s})^{3/2}
\left[1+\left(r/r_{\rm s}\right)^{3/2}\right]}~,
\end{displaymath}](/articles/aa/full/2002/41/aa2734/img204.gif) |
(19) |
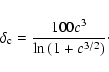 |
(20) |
| M(r) | = | (21) | |
| m(x) | = | (22) |
The derived parameters from each fit are given in
Table 5 and the best fit models are compared to the
data in Fig. 11. We find that the data are extremely
well described by the MQGSL profile across the entire radial range.
The NFW profile can also be used to describe the data, but shows a
small divergence at small radii (
![]() for the first 3
points). The radius corresponding to a density contrast of 500,
computed from the data, is indicated by an arrow. There is a slight
hint that the measured mass,
for the first 3
points). The radius corresponding to a density contrast of 500,
computed from the data, is indicated by an arrow. There is a slight
hint that the measured mass,
![]() ,
is higher than the MQGSL and NFW models (
,
is higher than the MQGSL and NFW models (
![]() and
and
![]() ,
respectively) around
that radius (see Sect. 9.3 for further discussion).
,
respectively) around
that radius (see Sect. 9.3 for further discussion).
Copyright ESO 2002