For each instrument, a global spectrum was extracted from all events
lying within
![]() from the cluster emission peak. This radial
range was chosen to maximise the S/N ratio, allowing us to check in
detail the consistency between the three cameras. Each global
spectrum was fitted with an absorbed MEKAL model with the redshift
fixed at z = 0.143. The normalisation for each instrument was left
as an additional free parameter. We excluded the energy bins around
the strong fluorescence lines of Ni, Cu & Zn from the pn spectrum fit.
These lines, present in the background, are not well subtracted by the
procedure described in Sect. 2 because they do not scale
perfectly with the continuum of the particle-induced background. In
all fits we used the following response matrices:
m1_thin1v9q20t5r6_all_15.rsp (MOS1), m2_thin1v9q20t5r6_all_15.rsp (MOS2) and epn_ef20_sY9_medium.rsp (pn).
from the cluster emission peak. This radial
range was chosen to maximise the S/N ratio, allowing us to check in
detail the consistency between the three cameras. Each global
spectrum was fitted with an absorbed MEKAL model with the redshift
fixed at z = 0.143. The normalisation for each instrument was left
as an additional free parameter. We excluded the energy bins around
the strong fluorescence lines of Ni, Cu & Zn from the pn spectrum fit.
These lines, present in the background, are not well subtracted by the
procedure described in Sect. 2 because they do not scale
perfectly with the continuum of the particle-induced background. In
all fits we used the following response matrices:
m1_thin1v9q20t5r6_all_15.rsp (MOS1), m2_thin1v9q20t5r6_all_15.rsp (MOS2) and epn_ef20_sY9_medium.rsp (pn).
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{MS2734f4a.eps}\par\vspace*{2mm}
\includegraphics[width=8.8cm,clip]{MS2734f4b.eps}
\end{figure}](/articles/aa/full/2002/41/aa2734/Timg107.gif) |
Figure 4:
XMM-Newton spectra of the cluster from
annuli 5 (
|
Fitting the data from all instruments above
![]() ,
with the
absorption fixed at the galactic value of
,
with the
absorption fixed at the galactic value of
![]() cm-2, we found inconsistent values for the temperature
derived with the MOS and pn cameras:
kT = 6.91-0.23+0.23 keV (MOS1),
cm-2, we found inconsistent values for the temperature
derived with the MOS and pn cameras:
kT = 6.91-0.23+0.23 keV (MOS1),
![]() (MOS2) and
(MOS2) and
![]() keV (pn). A better agreement between the
cameras, together with a lower
keV (pn). A better agreement between the
cameras, together with a lower ![]() value, are obtained if the
value, are obtained if the
![]() value is let free, but then the best fit
value is let free, but then the best fit ![]() values are significantly lower than the 21 cm value (see
Table 3). In other words the data presents an excess
at low energy as compared to an isothermal model absorbed with the
galactic hydrogen column density. This effect could be due to a true
soft excess component (e.g. Durret et al. 2002) and/or an
artifact due to remaining calibration uncertainties. In particular,
it is known that the EPIC-pn and MOS cameras show a relative flux
difference which increases with energy above
values are significantly lower than the 21 cm value (see
Table 3). In other words the data presents an excess
at low energy as compared to an isothermal model absorbed with the
galactic hydrogen column density. This effect could be due to a true
soft excess component (e.g. Durret et al. 2002) and/or an
artifact due to remaining calibration uncertainties. In particular,
it is known that the EPIC-pn and MOS cameras show a relative flux
difference which increases with energy above
![]() ,
resulting in
a MOS spectral slope flatter than the pn (Saxton 2002;
Griffiths et al. 2002).
,
resulting in
a MOS spectral slope flatter than the pn (Saxton 2002;
Griffiths et al. 2002).
We then performed a systematic study of the effect of imposing various
high and low-energy cutoffs for each instrument. The ![]() is
fixed to the 21 cm value. Having first found that progressive cutting
of the high energy channels had a negligible effect on the derived
temperatures, we then varied the low energy cutoff, for which the
results are shown in Table 3.
is
fixed to the 21 cm value. Having first found that progressive cutting
of the high energy channels had a negligible effect on the derived
temperatures, we then varied the low energy cutoff, for which the
results are shown in Table 3.
This table shows that there is an optimum low-energy cutoff for each
instrument, above which no amount of further cutting of the low-energy
response will significantly affect the temperature. The temperature
stabilises above a certain cutoff point for each instrument, this
being ![]() 0.6 keV for the MOS cameras and
0.6 keV for the MOS cameras and ![]() 1.0 keV for the
pn camera. The adoption of these low-energy cutoffs has the pleasing
effect of bringing the temperatures for each instrument into agreement
both with each other and with previous ASCA analysis. The
combined MOS+pn global temperature is
1.0 keV for the
pn camera. The adoption of these low-energy cutoffs has the pleasing
effect of bringing the temperatures for each instrument into agreement
both with each other and with previous ASCA analysis. The
combined MOS+pn global temperature is
![]() (
(![]() confidence for one interesting parameter,
confidence for one interesting parameter,
![]() for 1436 d.o.f.) in agreement with the results of
Ikebe et al. (2002), who find
for 1436 d.o.f.) in agreement with the results of
Ikebe et al. (2002), who find
![]() and Matsumoto et al. (2001), who
find
and Matsumoto et al. (2001), who
find
![]() ,
and marginally consistent with the
result of White (2000), who finds
,
and marginally consistent with the
result of White (2000), who finds
![]() .
.
It thus appears that the discrepancies observed by fitting the whole energy range are mostly due to some residual calibration uncertainties in the low-energy response of all instruments and/or a true soft excess. The scientific analysis of such a possible soft excess is beyond the scope of this paper. To minimise these effects, we adopted the low-energy cutoffs derived above for the spatially-resolved analysis discussed below.
These spectra were fitted using the absorbed MEKAL model described above; we fitted separately the spectra from each instrument as well as making a simultaneous MOS+pn fit, as detailed in Table B.1. All the temperatures are consistent within the respective errors. It is also evident from Fig. 5 that the form of each profile is similar. As a further test, we fitted the annular spectra with an absorbed MEKAL model with the absorption left as a free parameter. This produced profiles with, again, exactly the same shape, giving us high confidence in the form of the profile which we have derived.
The PSF of XMM-Newton is a potential cause of concern, especially in the
inner regions, where the bin sizes are small. To assess the effect of
the PSF, we first calculate a redistribution matrix, F(i,j), where F(i,j) is the fractional flux in annulus i coming from annulus j. These redistribution factors were derived from our best model of
the gas density profile, converted to emission measure profile and
convolved with the XMM-Newton PSF. The fractional contribution in each bin
of the emission coming from the bin, as well as all inner and outer
bins are plotted in Fig. 6. The PSF mostly affects
the central regions and, above
![]() ,
the contamination from
adjacent bins is less than
,
the contamination from
adjacent bins is less than ![]() .
.
We have a total of 30 spectra (10 annuli ![]() 3 cameras) to be
fitted with a model consisting of 10 MEKAL models
(corresponding to the 10 "true'' temperatures) absorbed by a common
(frozen) absorption. The normalisations of the MEKAL models, for annulus i, are linked by the factors F(i,j), such as to reflect the
contribution of each annulus j due to the PSF. In practice we ignore
any contributions at the less than
3 cameras) to be
fitted with a model consisting of 10 MEKAL models
(corresponding to the 10 "true'' temperatures) absorbed by a common
(frozen) absorption. The normalisations of the MEKAL models, for annulus i, are linked by the factors F(i,j), such as to reflect the
contribution of each annulus j due to the PSF. In practice we ignore
any contributions at the less than ![]() level. Each MEKAL model has
6 parameters, which, together with the absorption, makes 7. If we
fit the 30 spectra simultaneously, the model has
level. Each MEKAL model has
6 parameters, which, together with the absorption, makes 7. If we
fit the 30 spectra simultaneously, the model has
![]() parameters. XSPEC can only handle 1000 parameters,
(even if most of them are frozen), so we have to find a way to reduce
their total number. One way is to group the spectra, but for
this to work the spectra in each group need a common normalisation.
parameters. XSPEC can only handle 1000 parameters,
(even if most of them are frozen), so we have to find a way to reduce
their total number. One way is to group the spectra, but for
this to work the spectra in each group need a common normalisation.
We typically find differences of ![]()
![]() between the
normalisations of MOS and pn annular spectra (MOS1 and MOS2
normalisations are the same to within
between the
normalisations of MOS and pn annular spectra (MOS1 and MOS2
normalisations are the same to within ![]()
![]() ). We fit the global
spectrum discussed in Sect. 5.1 to find the overall
difference in normalisation between MOS and pn. We then checked that
the annular fit results were the same when the global difference in
normalisation was applied. This being so, we multiplied the pn annular
spectra by this factor to bring their normalisations into line with
those for the MOS cameras.
). We fit the global
spectrum discussed in Sect. 5.1 to find the overall
difference in normalisation between MOS and pn. We then checked that
the annular fit results were the same when the global difference in
normalisation was applied. This being so, we multiplied the pn annular
spectra by this factor to bring their normalisations into line with
those for the MOS cameras.
We now grouped the MOS and pn spectra of each annulus, giving 10 groups of 3 spectra, leaving us with
![]() parameters, enabling a simultaneous fit. We froze the
metallicity of each MEKAL model at the best-fit value found for each
projected annulus. The free parameters in the fit are then the
temperature and normalisation of each MEKAL model. The resulting
PSF-corrected profile is shown in Fig. 7 (
parameters, enabling a simultaneous fit. We froze the
metallicity of each MEKAL model at the best-fit value found for each
projected annulus. The free parameters in the fit are then the
temperature and normalisation of each MEKAL model. The resulting
PSF-corrected profile is shown in Fig. 7 (![]() errors). The PSF corrected results are entirely consistent with the
projected temperature profile, with systematic differences of about
half the
errors). The PSF corrected results are entirely consistent with the
projected temperature profile, with systematic differences of about
half the ![]() errors in the first 3 bins and smaller beyond.
This result is not surprising, since the profile is relatively flat.
Consideration of the PSF has a much smaller effect on the
temperature profile of A1413 than for the bright cooling flow cluster A1835 at z=0.25 (Markevitch 2002; Majerowicz
et al. 2002). In contrast to A1835, A1413 displays neither
an extremely steep rise in the central gas density, nor a sharp drop
in the temperature towards the center. As a result the contamination
of central bins is first smaller: for A1835, more than 1/3 of the
observed brightness at any radius is due to PSF scattering at smaller
radii (Markevitch 2002; Majerowicz et al. 2002)
while for A1413 this contamination is already less than
errors in the first 3 bins and smaller beyond.
This result is not surprising, since the profile is relatively flat.
Consideration of the PSF has a much smaller effect on the
temperature profile of A1413 than for the bright cooling flow cluster A1835 at z=0.25 (Markevitch 2002; Majerowicz
et al. 2002). In contrast to A1835, A1413 displays neither
an extremely steep rise in the central gas density, nor a sharp drop
in the temperature towards the center. As a result the contamination
of central bins is first smaller: for A1835, more than 1/3 of the
observed brightness at any radius is due to PSF scattering at smaller
radii (Markevitch 2002; Majerowicz et al. 2002)
while for A1413 this contamination is already less than ![]() at
at
![]() ,
and decreases beyond (Fig. 6). Secondly,
the smaller temperature gradient towards the center means that the
redistribution biases less the temperature determinations.
,
and decreases beyond (Fig. 6). Secondly,
the smaller temperature gradient towards the center means that the
redistribution biases less the temperature determinations.
A deprojected temperature profile was produced by first simultaneously
fitting the MOS and pn spectra of the outer annulus with a MEKAL model
absorbed by a fixed galactic column density. The spectrum of the next
annulus inward was then fitted with a two-temperature model with the
parameters of one of the models fixed to the best-fitting values
derived for the outer spectrum. The normalisation of each fixed model
must account for the volume within the outer shell projected along the
line of sight toward the next shell inward. Furthermore, as the gas
density profile is not flat, the normalisation must also account for
this effect. We model the gas density profile using the parameters
from the best-fit KBB model described in Sect. 4. The
normalisations are then adjusted by the emission weighted volume
factors. This process was continued inward, adding a MEKAL model for
each annulus, with the parameters of the outer annulus models frozen
to their previously determined best-fit values. The abundances of the
two outer annuli were frozen to the global value, so for these fits
the free parameter is the temperature. For all other annuli both the
temperature and abundance were free parameters. The deprojected
temperature profile is shown compared to the projected profile in
Fig. 7. In practice we find very little difference
between the projected and deprojected results. The jump in the
temperature of the ninth annulus is somewhat an artifact of the
fitting process. In this case the software tries to compensate for
the contribution of the low temperature found in the tenth (and
first-fitted) annulus by putting a higher temperature in the
subsequent annular bin. The error on the tenth temperature is large,
the contribution of the outer emission in the ninth bin depends on the
actual cluster extent and thus the deprojected ninth temperature is
probably more uncertain than found in this simple procedure. Note,
however, that the projected and deprojected temperatures agree well
within the ![]() errors.
errors.
In summary, we find that neither a consideration of the PSF or
projection effects substantially changes the form of the temperature
profile. The profiles obtained by taking into account these effects
are consistent with the projected profile, within the ![]() errors. For all subsequent analysis, we thus used the projected
profile.
errors. For all subsequent analysis, we thus used the projected
profile.
We now consider the scaled temperature profile,
![]() ,
where
,
where ![]() is the average temperature and x is the
scaled radius, normalised to r200. r200 is estimated from
the average temperature
is the average temperature and x is the
scaled radius, normalised to r200. r200 is estimated from
the average temperature ![]() and the r200-T relation of
EMN96 at the cluster redshift.
and the r200-T relation of
EMN96 at the cluster redshift. ![]() is estimated by fitting
the global spectrum, extracted from the
is estimated by fitting
the global spectrum, extracted from the
![]() region, i.e. outside the possible cooling flow region (see below). We
found
region, i.e. outside the possible cooling flow region (see below). We
found
![]() (
(![]() error). Note
that the temperature profile is determined up to
error). Note
that the temperature profile is determined up to ![]() 0.7 r200 or
0.7 r200 or ![]() r500.
r500.
We then modelled this projected temperature profile with a polytropic
model:
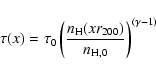 |
(10) |
We fitted the profile with all ![]() ,
,
![]() and
and ![]() parameters
fixed at the values best fitting the surface brightness profile
(Table 2), so that the free parameters for the fit are
parameters
fixed at the values best fitting the surface brightness profile
(Table 2), so that the free parameters for the fit are ![]() and
and ![]() .
When the whole radial range is fitted, we find
.
When the whole radial range is fitted, we find
![]() and
and
![]() ,
with
,
with
![]() .
If we then exclude the inner point, we find a better fit
with
.
If we then exclude the inner point, we find a better fit
with
![]() and
and
![]() ,
and
,
and
![]() .
The polytropic fits to the temperature profile are
shown in Fig. 8.
.
The polytropic fits to the temperature profile are
shown in Fig. 8.
We note that the fit is considerably better if the central point is excluded from the fit. The resulting polytropic profile rises to a peak in the centre which is not seen in the annular temperature determinations, which may lead us to believe that there is a small cooling flow (CF) at work in the very central regions. This possibility is discussed further in Sect. 6.
We further note that the derived value for the ![]() -parameter is
very close to isothermal and moreover, is not very sensitive to
whether the central bin is included in the fit. There is a
tantalising hint that the temperature profile may drop further in the
very outer regions, but the errors on this last data point are large
enough that it is easily compatible with the derived polytropic model.
-parameter is
very close to isothermal and moreover, is not very sensitive to
whether the central bin is included in the fit. There is a
tantalising hint that the temperature profile may drop further in the
very outer regions, but the errors on this last data point are large
enough that it is easily compatible with the derived polytropic model.
Copyright ESO 2002