

Up: Automatic observation rendering (AMORE)
Subsections
5 Results
AMORE has been tested for a wide range of setups.
The results in Table A.1 indicate that AMORE
give both acceptable and less acceptable solutions.
They are displayed in Figs. 3 and 4.
To better understand what goes on during the genetic evolution
we display the results from model A.1-40.
Figure 5 displays an example of the
evolution of the merit function F for a number of generations.
It shows how the initially dispersed individuals gradually find
their way, start to cluster together around generation 10,
and penetrate the region with acceptable solutions after
about 50 generations. After 100 generations the improvements
become marginal for this model.
Figure 6 displays for the same model A.1-40
the phenotypical changes of the CMD for several fitnesses during the
genetic evolution. The various panels show that the synthetic
CMD resembles better and better the "observed'' CMD when the
fitness improves. Note that at fitness fem=em0.05
one already gets for the eye appealing solutions.
Figure 7 shows the improvements of the
astrophysical parameters as a function of increasing fitness
for the models A.1-40 and A.1-51.
The panels for distance and extinction show that the
distance is systematically underestimated, while the
extinction is overestimated. But in general one notices that
the astrophysical parameters obtained from model
A.1-40 get quite close to the parameters
of the CMD to be matched.
![\begin{figure}
\par\includegraphics[width=18cm,clip]{aah3492f5.eps}
\end{figure}](/articles/aa/full/2002/36/aah3492/Timg100.gif) |
Figure 5:
Conception diagram of the
evolution of the genetic population of model A.1-40 during
the optimization process displayed in Fig. 7.
Frame a) shows the initial population and the frames
b)- l) show the population after several generations
up to generation = 400. The
outer
shaded region indicates solutions for which
the difference between the CMDs from the "observed'' and synthetic
population is on average
between 1-3em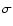 .
The inner shaded regions marks the region with
solutions for which the difference between the "observed'' and synthetic
CMDs are less than 1em .
The inner shaded regions marks the region with
solutions for which the difference between the "observed'' and synthetic
CMDs are less than 1em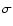 .
Such solutions are close to
perfect matches between the "observed'' and synthetic data
and are considered to belong to a group of solutions
for which one may say "too good to be true''.
The solid lines indicate
the 10em .
Such solutions are close to
perfect matches between the "observed'' and synthetic data
and are considered to belong to a group of solutions
for which one may say "too good to be true''.
The solid lines indicate
the 10em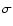 ,
20em ,
20em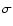 ,
30em ,
30em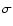 and 40em
and 40em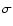 contours.
contours. |
5.1.1 Degeneracy of the parameter space
Table A.1 is displayed in
Fig. 3. The clustering in the figure provides
an indication that a degeneracy of the parameter space is present near
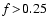 (i.e.
(i.e. 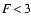 ,
see Eq. (1)).
Without a major computational effort
it will be difficult to obtain a significant improvement of the
parameters once
,
see Eq. (1)).
Without a major computational effort
it will be difficult to obtain a significant improvement of the
parameters once
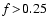 .
However,
.
However, 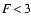 indicates a region in the (
indicates a region in the (
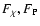 )-plane
for which the
systematic offset of the individual parameters
from its true value
are on average less than
)-plane
for which the
systematic offset of the individual parameters
from its true value
are on average less than
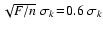 ,
see Sect. 2.9 for details.
In practice it turns out that
a strong correlation between three of the eight parameters
has the culprit; at least two of them have to change simultaneously
in the proper direction in order to improve the fitness
(see also Sect. 6.3).
They have an
average offset of
,
see Sect. 2.9 for details.
In practice it turns out that
a strong correlation between three of the eight parameters
has the culprit; at least two of them have to change simultaneously
in the proper direction in order to improve the fitness
(see also Sect. 6.3).
They have an
average offset of
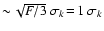 ,
while for the remaining parameters
this is
,
while for the remaining parameters
this is 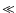
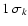 .
.
In addition, Fig. 4 displays the retrieved
parameters for all models
as a function of fitness. Note, that AMORE systematically
underestimates the distance of the test population. On the other hand,
the effect of this underestimation is in its turn partially canceled by
overestimating the extinction, the upper
age limit and the slope of the power-law IMF slightly
(see also Fig. 7).
Another clue we get from Fig. 4 is that the slope
of the SFR 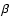 is very poorly constrained.
is very poorly constrained.
![\begin{figure}
\par\mbox{\hspace{5cm}\includegraphics[width=5cm,clip]{aa3492f6a....
...ps}\hspace{2mm}
\includegraphics[width=5cm,clip]{aa3492f6j.eps} }\end{figure}](/articles/aa/full/2002/36/aah3492/Timg107.gif) |
Figure 6:
Genetic evolution of the colour-magnitude diagram (CMD)
from the first test population.
Panel a) displays the original population to be matched.
The physical parameters for this population are described
Table 2 and Sect. 4.2. The CMD of the initial trial
population is shown in panel b). Panels c)- e) display the
resulting CMDs obtained with setup A.1-40 for different
fitnesses (see Sect 2.7). The fitnesses f = 0.05, f = 0.19and f = 0.27 are respectively reached after 20, 60 and 80 generations.
The dots in the panels b)- e) are used for each matching point,
while the red open stars
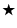 in panels c)- j)
are the points in the simulation which have no counterpart in the
original CMD. Panel f) displays the fitness f = 0.41
as obtained after
341 generations. Note that the CMDs of panels a) and f)
as well as c)- e) are visually almost indistinguishable.
Panels g)- j) displays the residuals between the simulated and
the original CMD ( a; green solid squares
in panels c)- j)
are the points in the simulation which have no counterpart in the
original CMD. Panel f) displays the fitness f = 0.41
as obtained after
341 generations. Note that the CMDs of panels a) and f)
as well as c)- e) are visually almost indistinguishable.
Panels g)- j) displays the residuals between the simulated and
the original CMD ( a; green solid squares
 ) are those points in the original which
have no counterpart in the simulation.
) are those points in the original which
have no counterpart in the simulation. |
![\begin{figure}
\par\includegraphics[width=18cm,clip]{ONLINE_FILES/A_SCANNER/evolve.ps}
\end{figure}](/articles/aa/full/2002/36/aah3492/Timg109.gif) |
Figure 7:
Panels a)- h) display the
convergence curves for the parameters of models A.1-40 (dotted line; fitness f=0.41)
and A.1-51 (long dashed line; fitness f=0.25).
The solid line in the frames a)- f) refers
to the value adopted for the original population.
The long, dot dashed line in frames i) and j)
shows the threshold values to be crossed for acceptable solutions,
i.e. F < 2 and
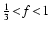 .
The short dashed area in frame j) marks the region
where degeneracy of the parameter space becomes noticeable
(see Sects. 6.3 for details). .
The short dashed area in frame j) marks the region
where degeneracy of the parameter space becomes noticeable
(see Sects. 6.3 for details). |
5.1.2 Determining values for pcross, rcross, rbrood,
pcreep, and pcorr
Looking at Table A.1, a result that is immediately obvious is
that pcorr = 0.0 has a strong
stabilizing effect on the simulation. Its effects overwhelm the
effects of the pcreep parameter and lock 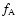 at a certain
value, which may be quite good (e.g. models 10, 11 and 12) or quite
poor (e.g. models 28, 29 and 30). Setting
at a certain
value, which may be quite good (e.g. models 10, 11 and 12) or quite
poor (e.g. models 28, 29 and 30). Setting
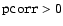 is thus
preferred to avoid getting locked in a low value for
is thus
preferred to avoid getting locked in a low value for 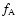 .
.
In order to compensate for this strong stabilizing effect, we also
evaluate in Table 3
the average fitness of the models when we exclude all models which
have pcorr = 0.0.
As expected, the rbrood parameter has a strong influence on the
amount of computational time needed. Although the models
with high values of rbrood are somewhat better than
models with low values, this effect is only marginal. Considering that a
high value of rbrood lessens the genetic variation in the gene
pool while increasing the computational time needed for a run with
several factors, it is desirable to have a low value of rbrood.
The different parameters are not independent, as can be seen from
Table A.1 and Table 3.
Simply taking the best options in Table 3 yields
model 134 for the case in which pcorr = 0.0 has not been corrected
for, a reasonable, but not an exceptionally good model.
5.2 Test 2: Rounding
Table 4 shows the effect of the accuracy of the retrieved
values of the parameters on the evaluation of the fitness. If one
applies a rounding to one or two significant digits it is not possible
to reproduce the expected fitness, i.e. the expected fitness drops
from
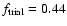 to
to
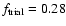 .
A better agreement can be obtained by reporting the values of
the parameters with the addition of one or more
(apparently insignificant) digit(s).
A renewed search (Table 4; round-v3)
circumvents the local optimum at
.
A better agreement can be obtained by reporting the values of
the parameters with the addition of one or more
(apparently insignificant) digit(s).
A renewed search (Table 4; round-v3)
circumvents the local optimum at
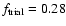 and
results in a near global fitness of
and
results in a near global fitness of
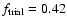 ,
which is close enough to the value expected.
,
which is close enough to the value expected.
The true 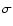 line in the table shows that both the
line in the table shows that both the
![$[Z]_{\rm high}$](/articles/aa/full/2002/36/aah3492/img81.gif) and the
and the 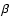 parameter are the weak links in the overall
parameter estimation (see also Fig 4).
parameter are the weak links in the overall
parameter estimation (see also Fig 4).
5.3 Test 3: Fixing parameters at the correct value
The results of fixing parameters at the correct value are listed in
Table A.2 and an example of the diagnostics is listed in
Table 6. Details of the individual setups
for these tests are given below.
In general, the results of the tests
for which one of the parameters was set
to the correct value were slightly better than the results
for the models for which all parameters are set free,
see Tables 4 and 5 for additional details.
This behaviour
is due to the fact that by forcing one parameter to a fixed value
the evolutionary path changes.
The models were selected from the results
with low and intermediate fitness given in Table A.1.
5.3.1 Fixed distance and extinction
Distance and extinction are
negatively correlated. When
both parameters are set free, a certain degree of degeneracy is to be
expected. Fixing one of the parameters at its correct value can break
this degeneracy.
The result depends strongly on the evolutionary path of the other
parameters.
The lower value for the
average fitness
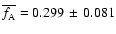 ,
when fixing the distance at the correct value,
is caused by the presence of
one outlier (see Table A.2),
which is caused by the age-metallicity degeneracy.
Excluding this value results in
an average fitness of
,
when fixing the distance at the correct value,
is caused by the presence of
one outlier (see Table A.2),
which is caused by the age-metallicity degeneracy.
Excluding this value results in
an average fitness of
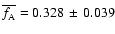 .
In general: the extinction
can be reliably retrieved when fixing the distance.
.
In general: the extinction
can be reliably retrieved when fixing the distance.
When considering a fixed extinction, the results show a strong variation in
both age and metallicity. It should also be noted that the average
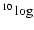 em(distance (pc))
retrieved is only 3.8953em
em(distance (pc))
retrieved is only 3.8953em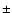 em0.0066.
This is more than one sigma away from the optimum value for the distance (see
Table 4). This is an indication that retrieval of the
distance by fixing the extinction is hampered by
the age-metallicity degeneracy. Therefore, the distance cannot be
reliably retrieved when fixing the extinction to its correct value.
em0.0066.
This is more than one sigma away from the optimum value for the distance (see
Table 4). This is an indication that retrieval of the
distance by fixing the extinction is hampered by
the age-metallicity degeneracy. Therefore, the distance cannot be
reliably retrieved when fixing the extinction to its correct value.
5.3.2 Fixed age and metallicity
Fixing one of the age limits results in values for both the age
and metallicity which are close to the input values.
This is due to the (partial) breaking of the
age-metallicity degeneracy. The distance-extinction
degeneracy remains. The results also suggest that the age-metallicity
degeneracy has a stronger impact on the fitness than the
distance-extinction degeneracy.
Fixing the upper metallicity limit to its
correct value shows that the values for age and metallicity
come closer to their original, input values.
This is quite in
contrast with the results obtained from fixing the
lower metallicity to its correct value.
Table A.2 shows that both the high metallicity
limit and the slope of the exponential SFR are not well
constrained. This behaviour can be accounted to the
implicit shape of the linear age-metallicity relation
adopted in the HRD-GST. The number of high metallicity
stars is smaller than the number of low metallicity
stars due to the adopted, exponentially decreasing (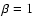 ),
star formation rate. The consequence is that the high metallicity
limit can be better determined when both the low and high
limits are determined in union.
),
star formation rate. The consequence is that the high metallicity
limit can be better determined when both the low and high
limits are determined in union.
Fixing the slope 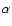 of the power-law IMF
to its correct value
ensures stability in the magnitude direction of the
CMD. This implies that the degeneracy in the colour dependent
parameters, like age, metallicity, and partly the
star formation rate, becomes more apparent.
Although the overall results are quite good,
only model A.2-14 is significantly affected by this
degeneracy. If we leave out model A.2-14
from the statistics the average
fitness becomes
of the power-law IMF
to its correct value
ensures stability in the magnitude direction of the
CMD. This implies that the degeneracy in the colour dependent
parameters, like age, metallicity, and partly the
star formation rate, becomes more apparent.
Although the overall results are quite good,
only model A.2-14 is significantly affected by this
degeneracy. If we leave out model A.2-14
from the statistics the average
fitness becomes
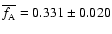 .
.
The exponential star formation rate parameter 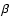 is tied to the age and metallicity range, see also
Sect. 5.3.2. Fixing the parameter
is tied to the age and metallicity range, see also
Sect. 5.3.2. Fixing the parameter 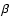 better constrains in particular
the upper metallicity limit. However, it does not
avoid that the genetic evolution enters into
a local age-metallicity gap, see Table A.2.
Excluding model A.2-34 improves the average fitness
in Table 5 to
better constrains in particular
the upper metallicity limit. However, it does not
avoid that the genetic evolution enters into
a local age-metallicity gap, see Table A.2.
Excluding model A.2-34 improves the average fitness
in Table 5 to
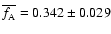 .
.
5.4 Test 4: Fixing parameters at the wrong value
The results of fixing the parameters at a
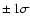 offset from its original value are listed in Table A.3.
An example of the diagnostics of these tests are given in
Table 8. Details of individual setups are given below.
offset from its original value are listed in Table A.3.
An example of the diagnostics of these tests are given in
Table 8. Details of individual setups are given below.
5.4.1 Erroneous distance
A wrong assumption about the distance gives in a vertical
shift in the CMD (all other parameters give a diagonal shift) and
cannot be masked out
through a correlated change of any of the other parameters.
This results in quite a wide range in the values of the other
parameters, except the value of 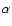 .
The unexpected result is that irrespective if
the distance is too short or too far: the power-law IMF slope
flattens!
.
The unexpected result is that irrespective if
the distance is too short or too far: the power-law IMF slope
flattens!
If the distance is overestimated there are more synthetic stars
present at fainter magnitudes. To get relatively more synthetic
stars at brighter magnitudes one needs to flatten the power-law IMF slope.
If the distance is underestimated then more synthetic stars are
present at brighter magnitudes. One expects that
a steeper power-law IMF slope is required as compensation.
This is not always true, see Table A.3.
Stars pop up at the lower end of the main sequence.
They are taken away from the stars located at brighter and brighter
magnitudes. One therefore requires also in this case a flatter IMF slope.
A flatter slope of the
power-law IMF can be a hint that the distance of the
stellar aggregate is wrong. Or it might be a hint that the zero point
of the adopted synthetic photometric system is different from the
actual photometric system used.
Recognizing that the slope is indeed flatter than
the majority of the other cases outlined in Table 4
one may start to explore the assumption that the
distance is wrong: release the constraint
during the next exploration.
The sensitivity to the distance implies that AMORE can be used to
determine the distance to a stellar aggregate quite reliably. A
bonus is that due to an initially wrongly assumed distance the
extinction is in most cases better constrained.
In (V, V-I) CMDs a strong correlation between
extinction, age and metallicity exists (see also Ng & Bertelli
1996 and references cited therein).
A higher value of the extinction can be compensated
by a younger age and/or a lower metallicity.
Indeed, the results in Table A.3 show that this
actually occurs for the lower age and metallicity limit.
The upper age and metallicity limit, however, drifts away in the
opposite direction to compensate
for "erroneous corrections'' applied by other parameters.
A higher value of the star formation index results in
a lower number of stars at the upper age metallicity limit.
To get a sufficient number of high metallicity stars
one has to stretch the upper metallicity limit to a
slightly higher value.
We further notice that a wrong value for the age and metallicity does not
affect the extinction significantly.
Our findings indirectly supports the method to determine
high resolution (
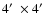 )
extinction maps towards the Galactic bulge by Schultheis
et al. (1999) with the data obtained for the DeNIS project
(Epchtein et al. 1997).
)
extinction maps towards the Galactic bulge by Schultheis
et al. (1999) with the data obtained for the DeNIS project
(Epchtein et al. 1997).
The slope of the power-law IMF is
very strongly constrained (Ng 1998) for the test population.
As a consequence the changes in the values of the
remaining parameters are not extremely large.
The slightly larger value of the slope 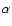 pushes slightly more synthetic stars to fainter magnitudes,
introducing a relative deficiency of stars at brighter magnitudes.
This is compensated through a younger age, a decrease
of the lower metallicity limit and an increase of the upper
metallicity limit. The higher value for the upper age
and metallicity limit compensates
in its turn for the overestimation of the exponential
star formation index.
pushes slightly more synthetic stars to fainter magnitudes,
introducing a relative deficiency of stars at brighter magnitudes.
This is compensated through a younger age, a decrease
of the lower metallicity limit and an increase of the upper
metallicity limit. The higher value for the upper age
and metallicity limit compensates
in its turn for the overestimation of the exponential
star formation index.
A lower value of 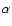 is partly compensated for by lowering the
upper age limit, lowering the lower metallicity limit and
overestimating the upper metallicity limit.
is partly compensated for by lowering the
upper age limit, lowering the lower metallicity limit and
overestimating the upper metallicity limit.
A larger index for an exponentially decreasing SFR pushes more stars
of the population to the blue edge of the CMD,
resulting in a slightly bluer stellar population. AMORE compensates
this by mainly increasing the upper metallicity limit,
i.e. reddening the synthetic stellar population.
A lower value for the SFR index has the opposite effect. AMORE compensates for the now slightly redder population by lowering
the upper metallicity limit, making the population bluer.


Up: Automatic observation rendering (AMORE)
Copyright ESO 2002
![\begin{figure}
\par\includegraphics[width=18cm,clip]{aah3492f5.eps}
\end{figure}](/articles/aa/full/2002/36/aah3492/Timg100.gif)
![\begin{figure}
\par\mbox{\hspace{5cm}\includegraphics[width=5cm,clip]{aa3492f6a....
...ps}\hspace{2mm}
\includegraphics[width=5cm,clip]{aa3492f6j.eps} }\end{figure}](/articles/aa/full/2002/36/aah3492/Timg107.gif)
![\begin{figure}
\par\includegraphics[width=18cm,clip]{ONLINE_FILES/A_SCANNER/evolve.ps}
\end{figure}](/articles/aa/full/2002/36/aah3492/Timg109.gif)