AMORE tries to find the best matching synthetic CMD to an observed CMD. Such a synthetic CMD contains for stellar aggregates the contribution of one or more stellar populations at the same distance. In the case of a CMD along a particular line of sight in our Galaxy the synthetic CMD can moreover contain the contribution of various populations with stars distributed at different distances.
In this paper we focus on the implementation and the performance of AMORE for the fitting of CMDs. For sake of argument only one, single stellar population has been considered. The implementation of automatic fitting CMDs with multiple stellar populations with stars at the same or different distances will be subject of forthcoming papers.
In the late-eighties Bertelli developed a code to generate synthetic
Hertzsprung-Russell diagrams (HRDs) from the isochrones computed by
the Padova group (cf. Chiosi et al. 1989). Initially the
synthetic colour-magnitude diagram (CMD) technique was applied mainly
in the studies of LMC open clusters![]() (see for example Bertelli et al. 1985, 1990 or Chiosi et al. 1989),
through which the amount of convective overshoot was calibrated
for the computation of a new generation of stellar evolutionary tracks.
Successive improvements were gradually applied when new sets of
evolutionary tracks (see Bertelli et al. 1994 for details)
were computed with improved radiative opacities (Iglesias et al.
1992).
(see for example Bertelli et al. 1985, 1990 or Chiosi et al. 1989),
through which the amount of convective overshoot was calibrated
for the computation of a new generation of stellar evolutionary tracks.
Successive improvements were gradually applied when new sets of
evolutionary tracks (see Bertelli et al. 1994 for details)
were computed with improved radiative opacities (Iglesias et al.
1992).
The backbone of HRD-ZVAR, the extended version of the HRD generator, is formed by the evolutionary tracks
computed by Bertelli et al. (1990;
![]() ),
Bressan et al. (1993;
),
Bressan et al. (1993;
![]() ),
and Fagotto et al. (1994a,b,c;
),
and Fagotto et al. (1994a,b,c;
![]() ,
0.004, 0.008, 0.050, 0.10).
The metallicities of the tracks follow the enrichment law
,
0.004, 0.008, 0.050, 0.10).
The metallicities of the tracks follow the enrichment law
![]() (see references cited in Chiosi
1996 and Pagel & Portinari 1998).
(see references cited in Chiosi
1996 and Pagel & Portinari 1998).
HRD-ZVAR indicates that the metallicity Z is not limited to the fixed values for which the evolutionary tracks have been computed, but is variable through interpolation between the metal-poorest and metal-richest tracks available inside the database of evolutionary tracks. In this way one is able to generate synthetic stellar populations with a smooth metallicity coverage. A prerequisite however is to use a complete and homogeneous library of evolutionary tracks and some improvements are expected if one adopts a grid of tracks with a smoother metallicity coverage.
HRD-ZVAR has been distributed (privately) to various research groups
and is also referred to as ZVAR![]() .
The version distributed, modified, and used by for example Aparicio
(1999), Gallart (1998), and Ng et al. (1996, 1997) is from now on referred to as
V1.0. Version V1.6 is used for the simulations and results presented
in this paper. This version contains a number of modifications and
improvements which speeds up the code and fixes some (rarely encountered)
bugs which interfered with the automatic minimization
process. Although various analysis methods are available, we limit
ourselves here to the description of the parameters related to the
HRD-ZVAR as adopted for AMORE.
.
The version distributed, modified, and used by for example Aparicio
(1999), Gallart (1998), and Ng et al. (1996, 1997) is from now on referred to as
V1.0. Version V1.6 is used for the simulations and results presented
in this paper. This version contains a number of modifications and
improvements which speeds up the code and fixes some (rarely encountered)
bugs which interfered with the automatic minimization
process. Although various analysis methods are available, we limit
ourselves here to the description of the parameters related to the
HRD-ZVAR as adopted for AMORE.
After selection of a set of tracks with fixed metallicity
and the choice of the parameters
![]() and
and
![]() ,
(the mass loss along the Red Giant Branch (RGB) and the Thermally
Pulsing Asymptotic Giant Branch (TP-AGB) phases respectively), the
major input to be specified for HRD-ZVAR are:
,
(the mass loss along the Red Giant Branch (RGB) and the Thermally
Pulsing Asymptotic Giant Branch (TP-AGB) phases respectively), the
major input to be specified for HRD-ZVAR are:
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{aah3492f1.eps}
\end{figure}](/articles/aa/full/2002/36/aah3492/Timg29.gif) |
Figure 1: AMORE flowchart: schematic diagram of the individual building blocks. PIKAIA outlines the direction of the evolution paths to be investigated. Input for the stellar population synthesis engine HRD-ZVAR is the Padova library of evolutionary tracks. The luminosity and effective temperature for each synthetic star of arbitrary metallicity is then transformed to an absolute magnitude in a photometric passband with the method outlined by Bertelli et al. (1994) and Bressan et al. (1994). The synthetic HRD is then "observed'' and "detected'' through a Monte Carlo "observing run'' with the HRD-GST. Note that an alternative route is possible with single stellar populations (SSPs). The synthetic CMD is compared with the observed diagram and a fitness parameter is subsequently communicated to PIKAIA, which suggests a new set of parameters for each trial. The iteration lasts for a user defined, fixed number of trials. POWELL's method of minimization is subsequently applied to get closer to the local or global minimum. After computation of the uncertainties for each parameter the evolutionary run is either aborted or a new PIKAIA cycle is started after shrinking the limits of the parameter space (see Sect. 2.9). |
HRD-ZVAR was integrated in a galactic model by Ng (1994, 1997ab). The HRD-GST (Galactic Software Telescope) has been applied in the studies of the galactic structure towards the Galactic Centre (Ng et al. 1995, 1996 and Bertelli et al. 1995, 1996) and other regions in our Galaxy (Ng et al. 1997). In this paper we do not require the full complexity of the structural properties from the GST model. We only use a limited number of options to "observe'' a synthetic HRD at the suggested distance and to simulate the photometric errors, extinction and crowding.
A table of the photometric errors, covering a specific magnitude interval per passband, is used and the program interpolates linearly to obtain the intermediate values. We assume for the simulation that the photometric errors are Gaussian distributed. A different description of the photometric errors will be used when published artificial star tests (Stetson & Harris 1988; Gallart et al. 1999) on an observational data set are indicative for a significant deviation from a Gaussian behaviour. The visual extinction is simulated with the average value provided and appropriately scaled to a value in different passbands. In the UBVRI passbands we adopted the scaling according to van de Hulst (1949; curve No. 15) and for the JHKLMN passbands we follow the scaling laws provided by Rieke & Lebofsky (1985). We do allow for some random scatter around the average extinction. However, we do not consider (yet) the effects due to patchiness of the extinction along the line of sight. Ng & Bertelli (1996) demonstrated that this is in first approximation, visually almost indistinguishable from a random scatter around an average extinction.
In many studies the observations are crowding limited, due to the increasing number of stars towards fainter magnitudes. Crowding gives rise to star blends which affects the magnitude and the colour of the stars. The group of stars will be detected as a single star with a magnitude equal to the sum of the stellar flux of the stars involved in the stellar blend. The remaining stars are "hidden'' from detection.
The blends are well described as unresolved, apparent binaries. The simulation of apparent binaries is made with an iteratively improved blending probability, which is defined as the probability that a star within a given ensemble of stars might blend with another star from the same population. Each synthetic star within a stellar population is tested against the blending probability.
The percentage of artificial binaries is with this scheme about twice the blending factor. The blending factor in different passbands is not necessarily the same and the occurrence of star blends is furthermore not necessarily correlated, due to possible differences in the exposure time or seeing conditions.
The fainter companion stars of artificial binaries will give rise to incompleteness of the synthetic stellar sample. This allows us to map the synthetic stellar completeness function, which can be compared directly with the completeness function obtained from artificial star tests from the observed stellar sample.
In the CMD to be analysed we assume implicitly that,
between the observed and synthetic photometric system,
the uncertainty in the magnitude zeropoint is smaller than
the uncertainty in the zeropoint of the colour,
see Carraro et al. (1999), and references cited therein.
We allow for this reason the possibility that a small zeropoint
shift might be present between the colours of these systems.
Although straightforward, the generation of a large number of synthetic HRDs with each their own specific age-metallicity range, star formation history and initial mass function can be a time consuming task, because of the repetition of many calculations to generate one diagram. Figure 1 indicates that an alternative route with single stellar populations (SSPs) is available for the automated analysis. However, this method requires the computation of a large, regular grid of SSPs for different age-metallicity ranges and IMFs. The star formation history and age-metallicity range are the result of the linear combination of the SSPs. The time spent on computations of new CMDs thus can be greatly reduced through the use of probability density diagrams. However, this is not our prime objective. Our present goal is to develop an automated fitting method, which compares on a star by star basis, and to demonstrate its potential. Optimization for speed is not yet our primary concern. Moreover, the generation of one synthetic CMD with 5000 stars takes about 0.75 s on a PC equipped with a 200 MHz Pentium processor. This is a good indication that our present version of the software tool is performing at an acceptable speed. We refer to Dolphin (1997,2001,2002) and Olsen (1999) for a description of a method using SSPs.
| initial | PIKAIA | parameter | comment |
| value | default | identifier | |
| 100 | 100 | np | the number of individuals per population |
| 20 | 500 | ngen | number of generations |
| 2 | 5 | nd | number of digits encoding accuracy |
| 2 | 2 | imut | mutation mode, imut = 2 then pmut = [pmutmn,pmutmx] |
| 0.005 | 0.005 | pmut | initial mutation rate |
| 0.005 | 0.005 | pmutmn | minimum mutation rate |
| 0.35 | 0.25 | pmutmx | maximum mutation rate |
| 0.95 | 1.0 | fdif | fitness differential |
| 3 | 1 | irep | reproduction plan |
| 0 | 1 | ielite | elitism |
| 0 | 0 | ivrb | verbose mode |
The PIKAIA optimization package (V1.0; public domain) was developed by Charbonneau (1995) and a full description of this package is given by Charbonneauem&emKnapp (1996). PIKAIA has been used successfully in a wide range of astrophysical applications (e.g. Bobinger 2000; Charbonneau et al. 1998; Gibson & Charbonneau 1998; Kaastra et al. 1996; Kennelly et al. 1996; Lamontagne et al. 1996; McIntosh et al. 1998; Metcalfe 1999; Mewe et al. 1996; Noyes et al. 1997; Saha 1998; Wahde 1998).
PIKAIA is based on a genetic algorithm (Holland 1975; Goldberg 1989; Davis 1991; De Jong 1993), and is in principle not a function optimizer, but it does this extremely well. It searches for, locks on to, and pins down an optimal solution in a way, which is conceptually comparable to biological evolution through natural selection. Genetic algorithms are capable to explore and find in a robust way an optimum, but not necessarily the best, setting for a particular problem. In our case this comes down to minimizing the difference between a synthetic and an observed CMD by evolving the astrophysical parameters that define the shape of the CMD (see Table 2 and Sects. 2.10 and 3). We follow the generally accepted biological terminology for the description of a genetic algorithm.
A genetic algorithm makes use of a reduced version of the evolutionary process. The gene pool, i.e. the set of parameters to be optimized, and its associated phenotypic population evolves in response to
PIKAIA has 12 flow control parameters which are discussed
by Charbonneau (1995) to whom we refer
for a detailed description. We limit ourselves
to a short summary and the purposes of these control parameters:
np defines the number of individuals in a population;
ngen specifies the number of generations that the population
is evolving;
nd is number of digits encoding
accuracy![]() used for the parameters;
pcross is the probability that a crossover occurs between
the chromosomes of the parents;
imut,
pmut, pmutmn,
and pmutmx specify the mutation mode, the mutation rate
(the initial mutation rate if the rate spans the range from
pmutmn to pmutmx for
imutem=em2),
and the minimum and maximum mutation rate;
fdif the fitness differential controls the selection of
the individuals for breeding through their fitness;
irep defines the reproduction plan to be followed;
ielite defines if the fittest individual can or cannot
be selected for replacement; and
ivrb specifies verbose mode for extra on screen
information during the evolutionary run.
used for the parameters;
pcross is the probability that a crossover occurs between
the chromosomes of the parents;
imut,
pmut, pmutmn,
and pmutmx specify the mutation mode, the mutation rate
(the initial mutation rate if the rate spans the range from
pmutmn to pmutmx for
imutem=em2),
and the minimum and maximum mutation rate;
fdif the fitness differential controls the selection of
the individuals for breeding through their fitness;
irep defines the reproduction plan to be followed;
ielite defines if the fittest individual can or cannot
be selected for replacement; and
ivrb specifies verbose mode for extra on screen
information during the evolutionary run.
Table 1 holds a list of the PIKAIA flow parameters which were kept constant during all the simulations described in this paper. In the following subsections we describe the extensions added to the 12 flow parameters of PIKAIA.
The crossover operator is very effective in a global exploration of
the full parameter space and is in a way comparable to a variational
calculus method. A one-point crossover scheme, see
Fig. 2, is sometimes inadequate to combine and
pass on certain features encoded on the chromosomes (Michalewicz
1996) to its offspring. In some cases only a
correlated modification of a number of genes, say 2, will result in a
fitter offspring. This can, for example, be mimicked through the
application of a two- or multi-point crossover scheme. PIKAIA has
been extended with the control parameter rcross to handle a
multi-point crossover operation. For example: rcrossem=em1 represents the default one-point crossover,
while rcrossem=em2.3 represents a "2.3-point'' crossover:
i.e. a two-point and three-point crossover for respectively 70% and
30% of the cases (
![]() ).
).
An important drawback of genetic algorithms is that
the crossover operator is for about 75% of the time
lethal to its offspring, i.e. it produces children which
are not as fit as their parents (Banzhaf et al. 1998).
To avoid missing, potentially, fitter offspring and to
reduce the destructive effect of the crossover operator
we have incorporated brood recombination in PIKAIA
through a new control parameter rbrood.
The default PIKAIA reproduction scheme is obtained with
rbroodem=em1, i.e. two parents breed once and
produce two new individuals.
With
![]() the parents are allowed
to breed on average 3.5 times to produce a larger offspring (in this
case 7 on average).
For rbroodem>em1 one ends up with more
than two offspring. PIKAIA on the other hand expects from each pair
of parents only two children. This constraint was obeyed
in order not to significantly alter the global behaviour
of PIKAIA. Therefore, in order to avoid an exponential growth of
the population for rbroodem
the parents are allowed
to breed on average 3.5 times to produce a larger offspring (in this
case 7 on average).
For rbroodem>em1 one ends up with more
than two offspring. PIKAIA on the other hand expects from each pair
of parents only two children. This constraint was obeyed
in order not to significantly alter the global behaviour
of PIKAIA. Therefore, in order to avoid an exponential growth of
the population for rbroodem![]() em1,
only the fittest two individuals of the local offspring
survive
em1,
only the fittest two individuals of the local offspring
survive![]() and enter the global population for a fitness
evaluation from which a selection is made for further breeding.
The extra breeding increases the computational effort considerably,
due to a larger number of function evaluations. The advantage is a more
rapid increase of fitter individuals through the selection
of effective crossovers from good recombinations. On the other hand, a
rapid increase of fitter individuals might lead to a premature
convergence to a local minimum, due to a smaller variance in the genetic pool.
and enter the global population for a fitness
evaluation from which a selection is made for further breeding.
The extra breeding increases the computational effort considerably,
due to a larger number of function evaluations. The advantage is a more
rapid increase of fitter individuals through the selection
of effective crossovers from good recombinations. On the other hand, a
rapid increase of fitter individuals might lead to a premature
convergence to a local minimum, due to a smaller variance in the genetic pool.
We further introduced the "creep'' mutation (Charbonneau & Knapp 1996) in order to overcome the so-called "Hamming Wall'' problem, i.e. the inability to cross in a decimal encoding scheme certain boundaries with a one-point mutation operator. The creep parameter pcreep defines the probability that a gene in the pool undergoes a "standard'' mutation (change digit randomly in the range 0-9) or the "creep'' mutation (add or subtract one from the current value of the digit). We adopted as default equal weight for the occurrence of a "creep'' or "standard'' mutation.
We modified PIKAIA's uniform mutation mode. In the majority of the cases we require a (anti-)correlated change between two or more parameters (see Sect. 6.2). In a standard mutation scheme convergence might be slow if one has to wait for the simultaneous occurrence of a favourable (anti-)correlated mutation of two specific parameters in order to improve the fitness. We introduced an extra parameter pcorr which defines the probability that a correlated mutation occurs. If this is not the case the standard mutation scheme is chosen. Otherwise we allowed that in 50% of the cases the mutations of two genes (igen1 and igen2 are extra input parameters added to the modified version of PIKAIA) are more relevant than the mutations occurring in other parameters. For the remaining 50% of the cases the two genes are determined stochastically. Additional details about the adopted values of the control parameters are given in Sect. 2.10 and Table A.1.
![]() and
and ![]() are respectively defined as:
are respectively defined as:
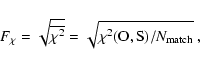 |
(3) |
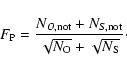 |
(4) |
| # | parameter | value | lower limit | upper limit | description |
| 1 | log d | 3.7 | 3.6 | 4.0 | log of distance |
| 2 | 0.30 | - 0.001 | 0.5 | extinction | |
| 3 |
|
9.5 | 9.0 | 10.3 | log lower age limit |
| 4 |
|
- 0.90 | - 1.69897 | 0.69897 | log lower metallicity limit |
| 5 | 1.35 | 1.001 | 3.5 | IMF slope | |
| 6 |
|
9.6 | 9.0 | 10.3 | log upper age limit |
| 7 | [Z]
|
0.30 | - 1.69897 | 0.69897 | log upper metallicity limit |
| 8 | 1.0 | - 2.00 | 5.00 | SFR slope |
The formal 1![]() uncertainty of each parameter k,
see Table 4,
is obtained through variation of this parameter and
by minimizing the function
uncertainty of each parameter k,
see Table 4,
is obtained through variation of this parameter and
by minimizing the function
![]() .
Conceptually, this is similar to moving the merit function
in the
.
Conceptually, this is similar to moving the merit function
in the
![]() - plane away from its optimum setting,
to the nearest position on a contour +1
- plane away from its optimum setting,
to the nearest position on a contour +1![]() higher.
The associated fitness
function
higher.
The associated fitness
function
![]()
![]() is:
is:
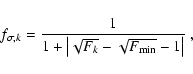 |
(5) |
We implemented a hybrid optimizer in which we use PIKAIA to explore the parameter space and then use POWELL's minimization algorithm (Powell 1964; Press et al. 1986) to pin down the nearest local or global minimum through a direction set method which produces N mutually conjugate (non-interfering) directions. For details and an excellent description of this algorithm we refer to Press et al. and references cited therein.
A hybrid minimization strategy is used, because PIKAIA is by definition not a function optimizer, but it tends to get close near a (local) optimum. POWELL is used to get even closer to the (local) optimum. If we had landed in a local optimum then we needed PIKAIA to jump out of it. The origin of our need for a hybrid search strategy is comparable to the minimization problems encountered by Harris & Zaritsky (2001).
We implemented a dynamic, scalable parameter range in our search for an optimum set of parameters. The parameter range shrinks after each optimization cycle with POWELL. This leads to an improved accuracy in the results with a fixed number of digits encoding accuracy.
The automated re-scaling of the parameter range improves the resolution of the exploration of the search grid. In addition, due to the re-scaling one may circumvent partial degeneracy of the parameters.
The global function
![]() gives the global distance to the minimum
in terms of
gives the global distance to the minimum
in terms of
![]() .
If we have n parameters then each parameter k is in a simple approach
on average about
.
If we have n parameters then each parameter k is in a simple approach
on average about
![]() away from its optimum
value,
because we assume that
away from its optimum
value,
because we assume that
AMORE uses in essence two different sets of parameters as input. One set contains program flow control parameters and information about the observational data to be simulated: the photometric errors and crowding factors per passband, a shift of the zeropoint of the colours due to a difference between the observed and synthetic photometric system, and the spread around the average extinction value to account partly for the differential reddening in a field.
![\begin{figure}
\par\includegraphics[width=10.5cm,clip]{aah3492f3.eps}
\end{figure}](/articles/aa/full/2002/36/aah3492/Timg70.gif) |
Figure 3:
Evolutionary status for all the trial models
(filled dots; see Table A.1
for details) for each population after 400 generations, see also
Fig. 4.
The filled star
|
The other set of input parameters is used by PIKAIA and can be divided into two parts (see Tables 1 and 2). One part contains the PIKAIA control parameters. The other part contains the lower and upper limits of the astrophysical parameters to be optimized as well as an initial guess for the value of those parameters (first column of Table 2, resulting HRD in Fig. 6b). These parameters are a combination of the synthetic population's intrinsic properties, i.e. age, metallicity, slope of the power-law IMF and the index of the exponential SFR. In our case we allow for age and metallicity not to be restricted to one fixed value, but to cover a specific range (see Table 2).
In addition, there are two parameters which mimic the synthetic population's behaviour as placed in a mockup version of our Galaxy. These parameters are the distance from the Sun and the average extinction.
In total we thus have 8 free parameters which AMORE has to optimize simultaneously.
Copyright ESO 2002