Online Material

 

 

Table A.1: AMORE with the test population as specified in Sect. 4.3.1. See 2.6.2, 2.6.3, 2.6.4, 2.6.5 and 4.2 for additional details. pcross is the crossover probability, rcross is the multi-point crossover rate, rbrood determines the amount of offspring two parents can have, pcreep is the creep mutation rate and pcorr the correlated mutation rate. The generation number indicates at which generation the resulting fitness value 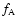$f_{\rm A}$obtained with AMORE first emerged.

model	pcross	rcross	rbrood	pcreep	pcorr	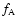$f_{\rm A}$	generation
1	0.85	1.00	1.00	0.0	0.0	0.17266	361
2	0.85	1.00	1.00	0.3	0.0	0.17266	361
3	0.85	1.00	1.00	0.7	0.0	0.17266	361
4	0.85	1.00	1.00	0.0	0.3	0.27551	221
5	0.85	1.00	1.00	0.0	0.7	0.26830	221
6	0.85	1.00	1.00	0.3	0.3	0.30488	381
7	0.85	1.00	1.00	0.7	0.3	0.32005	341
8	0.85	1.00	1.00	0.3	0.7	0.32167	201
9	0.85	1.00	1.00	0.7	0.7	0.38310	341
10	0.50	1.00	1.00	0.0	0.0	0.35662	381
11	0.50	1.00	1.00	0.3	0.0	0.35662	381
12	0.50	1.00	1.00	0.7	0.0	0.35662	381
13	0.50	1.00	1.00	0.0	0.3	0.34961	281
14	0.50	1.00	1.00	0.0	0.7	0.17008	261
15	0.50	1.00	1.00	0.3	0.3	0.36025	381
16	0.50	1.00	1.00	0.7	0.3	0.24048	261
17	0.50	1.00	1.00	0.3	0.7	0.23956	321
18	0.50	1.00	1.00	0.7	0.7	0.29463	321
19	0.85	2.00	1.00	0.0	0.0	0.31700	384
20	0.85	2.00	1.00	0.3	0.0	0.31700	384
21	0.85	2.00	1.00	0.7	0.0	0.31700	384
22	0.85	2.00	1.00	0.0	0.3	0.25740	341
23	0.85	2.00	1.00	0.0	0.7	0.35805	341
24	0.85	2.00	1.00	0.3	0.3	0.34120	181
25	0.85	2.00	1.00	0.7	0.3	0.31290	141
26	0.85	2.00	1.00	0.3	0.7	0.30913	341
27	0.85	2.00	1.00	0.7	0.7	0.32212	261
28	0.50	2.00	1.00	0.0	0.0	0.16122	261
29	0.50	2.00	1.00	0.3	0.0	0.16122	261
30	0.50	2.00	1.00	0.7	0.0	0.16122	261
31	0.50	2.00	1.00	0.0	0.3	0.36796	381
32	0.50	2.00	1.00	0.0	0.7	0.28494	381
33	0.50	2.00	1.00	0.3	0.3	0.27263	381
34	0.50	2.00	1.00	0.7	0.3	0.16352	301
35	0.50	2.00	1.00	0.3	0.7	0.35149	301
36	0.50	2.00	1.00	0.7	0.7	0.34031	381
37	0.85	3.00	1.00	0.0	0.0	0.38297	301
38	0.85	3.00	1.00	0.3	0.0	0.38297	301
39	0.85	3.00	1.00	0.7	0.0	0.38297	301
40	0.85	3.00	1.00	0.0	0.3	0.41019	341
41	0.85	3.00	1.00	0.0	0.7	0.32012	381
42	0.85	3.00	1.00	0.3	0.3	0.36840	341
43	0.85	3.00	1.00	0.7	0.3	0.31281	361
44	0.85	3.00	1.00	0.7	0.3	0.31281	361
45	0.85	3.00	1.00	0.3	0.7	0.30571	381
46	0.50	3.00	1.00	0.0	0.0	0.15614	301
47	0.50	3.00	1.00	0.3	0.0	0.15614	301
48	0.50	3.00	1.00	0.7	0.0	0.15614	301
49	0.50	3.00	1.00	0.0	0.3	0.23392	301
50	0.50	3.00	1.00	0.0	0.7	0.16274	221
51	0.50	3.00	1.00	0.3	0.3	0.25123	281
52	0.50	3.00	1.00	0.7	0.3	0.27151	261
53	0.50	3.00	1.00	0.3	0.7	0.35597	301

 

Table A.1: continued.

model	pcross	rcross	rbrood	pcreep	pcorr	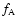$f_{\rm A}$	generation
54	0.50	3.00	1.00	0.7	0.7	0.27743	361
55	0.85	1.00	2.00	0.0	0.0	0.36221	161
56	0.85	1.00	2.00	0.3	0.0	0.36221	161
57	0.85	1.00	2.00	0.7	0.0	0.36221	161
58	0.85	1.00	2.00	0.0	0.3	0.16284	261
59	0.85	1.00	2.00	0.0	0.7	0.30251	381
60	0.85	1.00	2.00	0.3	0.3	0.32133	361
61	0.85	1.00	2.00	0.7	0.3	0.33565	361
62	0.85	1.00	2.00	0.3	0.7	0.27452	341
63	0.85	1.00	2.00	0.7	0.7	0.34660	301
64	0.50	1.00	2.00	0.0	0.0	0.27683	381
65	0.50	1.00	2.00	0.3	0.0	0.27683	381
66	0.50	1.00	2.00	0.7	0.0	0.27683	381
67	0.50	1.00	2.00	0.0	0.3	0.16833	201
68	0.50	1.00	2.00	0.0	0.7	0.38586	321
69	0.50	1.00	2.00	0.3	0.3	0.34390	361
70	0.50	1.00	2.00	0.7	0.3	0.33531	241
71	0.50	1.00	2.00	0.3	0.7	0.32646	221
72	0.50	1.00	2.00	0.7	0.7	0.34591	381
73	0.85	1.00	4.00	0.0	0.0	0.34607	221
74	0.85	1.00	4.00	0.3	0.0	0.34607	221
75	0.85	1.00	4.00	0.7	0.0	0.34607	221
76	0.85	1.00	4.00	0.0	0.3	0.32143	361
77	0.85	1.00	4.00	0.0	0.7	0.27159	381
78	0.85	1.00	4.00	0.3	0.3	0.26001	221
79	0.85	1.00	4.00	0.7	0.3	0.19802	241
80	0.85	1.00	4.00	0.3	0.7	0.33032	381
81	0.85	1.00	4.00	0.7	0.7	0.17799	341
82	0.50	1.00	4.00	0.0	0.0	0.27728	201
83	0.50	1.00	4.00	0.3	0.0	0.27728	201
84	0.50	1.00	4.00	0.7	0.0	0.27728	201
85	0.50	1.00	4.00	0.0	0.3	0.35783	381
86	0.50	1.00	4.00	0.0	0.7	0.28070	341
87	0.50	1.00	4.00	0.3	0.3	0.33717	381
88	0.50	1.00	4.00	0.7	0.3	0.18275	341
89	0.50	1.00	4.00	0.3	0.7	0.24795	361
90	0.50	1.00	4.00	0.7	0.7	0.28384	341
91	0.85	2.00	2.00	0.0	0.0	0.29274	261
92	0.85	2.00	2.00	0.3	0.0	0.29274	261
93	0.85	2.00	2.00	0.7	0.0	0.29274	261
94	0.85	2.00	2.00	0.0	0.3	0.24259	381
95	0.85	2.00	2.00	0.0	0.7	0.26513	161
96	0.85	2.00	2.00	0.3	0.3	0.33411	361
97	0.85	2.00	2.00	0.7	0.3	0.25808	121
98	0.85	2.00	2.00	0.3	0.7	0.35686	341
99	0.85	2.00	2.00	0.7	0.7	0.37254	399
100	0.50	2.00	2.00	0.0	0.0	0.28259	361
101	0.50	2.00	2.00	0.3	0.0	0.28259	361
102	0.50	2.00	2.00	0.7	0.0	0.28259	361
103	0.50	2.00	2.00	0.0	0.3	0.34559	341
104	0.50	2.00	2.00	0.0	0.7	0.39464	320
105	0.50	2.00	2.00	0.3	0.3	0.27112	181
106	0.50	2.00	2.00	0.7	0.3	0.29866	321
107	0.50	2.00	2.00	0.3	0.7	0.23660	181
108	0.50	2.00	2.00	0.7	0.7	0.35769	261
109	0.85	2.00	4.00	0.0	0.0	0.32628	181
110	0.85	2.00	4.00	0.3	0.0	0.32628	181
111	0.85	2.00	4.00	0.7	0.0	0.32628	181

 

Table A.1: continued.

model	pcross	rcross	rbrood	pcreep	pcorr	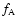$f_{\rm A}$	generation
111	0.85	2.00	4.00	0.7	0.0	0.32628	181
112	0.85	2.00	4.00	0.0	0.3	0.26910	361
113	0.85	2.00	4.00	0.0	0.7	0.37278	389
114	0.85	2.00	4.00	0.3	0.3	0.31434	241
115	0.85	2.00	4.00	0.7	0.3	0.18222	321
116	0.85	2.00	4.00	0.3	0.7	0.26176	341
117	0.85	2.00	4.00	0.7	0.7	0.19495	241
118	0.50	2.00	4.00	0.0	0.0	0.17656	361
119	0.50	2.00	4.00	0.3	0.0	0.17656	361
120	0.50	2.00	4.00	0.7	0.0	0.17656	361
121	0.50	2.00	4.00	0.0	0.3	0.17248	181
122	0.50	2.00	4.00	0.0	0.7	0.27790	381
123	0.50	2.00	4.00	0.3	0.3	0.17117	221
124	0.50	2.00	4.00	0.7	0.3	0.36171	381
125	0.50	2.00	4.00	0.3	0.7	0.38431	392
126	0.50	2.00	4.00	0.7	0.7	0.31711	400
127	0.85	3.00	2.00	0.0	0.0	0.16288	161
128	0.85	3.00	2.00	0.3	0.0	0.16288	161
129	0.85	3.00	2.00	0.7	0.0	0.16288	161
130	0.85	3.00	2.00	0.0	0.3	0.34149	341
131	0.85	3.00	2.00	0.0	0.7	0.33630	281
132	0.85	3.00	2.00	0.3	0.3	0.24355	301
133	0.85	3.00	2.00	0.7	0.3	0.33731	221
134	0.85	3.00	2.00	0.3	0.7	0.26283	201
135	0.85	3.00	2.00	0.7	0.7	0.25975	121
136	0.50	3.00	2.00	0.0	0.0	0.26047	221
137	0.50	3.00	2.00	0.3	0.0	0.26047	221
138	0.50	3.00	2.00	0.7	0.0	0.26047	221
139	0.50	3.00	2.00	0.0	0.3	0.26449	321
140	0.50	3.00	2.00	0.0	0.7	0.27116	281
141	0.50	3.00	2.00	0.3	0.3	0.31298	101
142	0.50	3.00	2.00	0.7	0.3	0.32952	201
143	0.50	3.00	2.00	0.3	0.7	0.25496	281
144	0.50	3.00	2.00	0.7	0.7	0.24888	221
145	0.85	3.00	4.00	0.0	0.0	0.34932	321
146	0.85	3.00	4.00	0.3	0.0	0.34932	321
147	0.85	3.00	4.00	0.7	0.0	0.34932	321
148	0.85	3.00	4.00	0.0	0.3	0.34687	381
149	0.85	3.00	4.00	0.0	0.7	0.32433	321
150	0.85	3.00	4.00	0.3	0.3	0.17152	141
151	0.85	3.00	4.00	0.7	0.3	0.30958	395
152	0.85	3.00	4.00	0.3	0.7	0.31341	398
153	0.85	3.00	4.00	0.7	0.7	0.27072	261
154	0.50	3.00	4.00	0.0	0.0	0.34272	101
155	0.50	3.00	4.00	0.3	0.0	0.34272	101
156	0.50	3.00	4.00	0.7	0.0	0.34272	101
157	0.50	3.00	4.00	0.0	0.3	0.30844	321
158	0.50	3.00	4.00	0.0	0.7	0.27009	361
159	0.50	3.00	4.00	0.3	0.3	0.17333	381
160	0.50	3.00	4.00	0.7	0.3	0.25621	361
161	0.50	3.00	4.00	0.3	0.7	0.39429	341
162	0.50	3.00	4.00	0.7	0.7	0.26150	361

 

 

Table A.2: Results of running AMORE with one of the astrophysical parameters fixed at its original value. These tests provide an indication about the influence of one parameter on the retrieval of the remaining parameters, see Sects. 4.3.3 and 5.3 for additional details.

parameter	model	$f_{\rm A}$	log d (pc)	$A_{\rm V}$	$\log t_{\rm low}$	$\log t_{\rm high}$	$[Z]_{\rm low}$	$[Z]_{\rm high}$	$\alpha$	$\beta$
log d	9	0.34897	3.90633	0.002	9.89178	9.95342	- 0.60089	0.19300	2.341	0.985
	14	0.35919	3.90633	- 0.001	9.88937	9.95245	- 0.60115	0.20684	2.341	1.111
	22	0.26617	3.90633	0.007	9.86685	9.95757	- 0.53389	0.30054	2.351	2.980
	34	0.31373	3.90633	0.001	9.87873	9.95335	- 0.57392	0.25198	2.341	1.613
	40	0.15102	3.90633	0.016	9.78469	10.12246	- 0.69199	0.07931	2.319	- 1.281
	52	0.35475	3.90633	0.012	9.89392	9.95002	- 0.59523	0.17305	2.338	0.936
$A_{\rm V}$	9	0.25192	3.89083	0.000	9.87519	9.98656	- 0.50206	0.34423	2.391	2.613
	14	0.23362	3.88471	0.000	9.88175	9.99802	- 0.50635	0.40461	2.424	3.682
	22	0.30930	3.89399	- 0.001	9.91339	9.98285	- 0.55292	0.20319	2.383	0.889
	34	0.17545	3.89688	0.001	9.80693	10.1395	- 0.66073	0.10056	2.339	- 1.338
	40	0.26131	3.89634	0.001	9.82335	9.96459	- 0.51903	0.44994	2.355	3.493
	52	0.41406	3.90592	0.000	9.90287	9.95544	- 0.59621	0.17710	2.350	1.003
log $t_{\rm low}$	9	0.34505	3.89687	0.030	9.90310	9.96292	- 0.59785	0.19586	2.358	1.028
	14	0.29609	3.90078	0.064	9.90308	9.93943	- 0.67152	0.10196	2.333	0.087
	22	0.34452	3.89289	0.026	9.90308	9.96482	- 0.57260	0.23664	2.362	1.435
	34	0.32855	3.89861	0.067	9.90309	9.94303	- 0.62670	0.14375	2.343	0.845
	40	0.35429	3.89657	0.014	9.90309	9.96685	- 0.56333	0.21007	2.358	1.130
	52	0.32296	3.89388	0.036	9.90309	9.96827	- 0.58340	0.21130	2.365	1.197
log $t_{\rm high}$	9	0.32414	3.89839	0.033	9.88329	9.95424	- 0.55256	0.26193	2.341	1.674
	14	0.25502	3.89455	0.036	9.85431	9.95425	- 0.52027	0.39343	2.351	3.455
	22	0.26055	3.90038	0.022	9.76480	9.95423	- 0.52358	0.52141	2.333	4.267
	34	0.36575	3.89772	0.046	9.90052	9.95424	- 0.60081	0.20274	2.352	1.251
	40	0.25141	3.89839	0.042	9.75973	9.95424	- 0.56527	0.52340	2.335	4.878
	52	0.37074	3.89458	0.066	9.91101	9.95424	- 0.62634	0.16462	2.361	1.046
log $[Z]_{\rm low}$	9	0.22556	3.89237	0.059	9.78605	9.96444	- 0.60205	0.48867	2.363	4.119
	14	0.32714	3.89352	0.031	9.89643	9.96409	- 0.60207	0.22149	2.354	0.907
	22	0.23902	3.89510	0.047	9.82960	9.95708	- 0.60205	0.45203	2.363	3.709
	34	0.27029	3.89729	0.040	9.84880	9.95803	- 0.60207	0.31992	2.327	1.756
	40	0.28851	3.89175	0.028	9.94114	9.97064	- 0.60206	0.10911	2.399	0.305
	52	0.26238	3.89419	0.041	9.87970	9.96558	- 0.60207	0.29439	2.375	2.197
log $[Z]_{\rm high}$	9	0.32971	3.89633	0.044	9.90542	9.96035	- 0.58239	0.17609	2.363	1.182
	14	0.39924	3.89593	0.038	9.90880	9.96147	- 0.58144	0.17608	2.360	1.009
	22	0.40156	3.89579	0.053	9.90555	9.95702	- 0.60422	0.17608	2.357	1.057
	34	0.31199	3.89306	0.017	9.92288	9.97460	- 0.57681	0.17610	2.384	0.872
	40	0.35466	3.89952	0.044	9.90467	9.95065	- 0.61730	0.17609	2.349	1.010
	52	0.36582	3.89853	0.042	9.90077	9.95166	- 0.60430	0.17608	2.342	0.878
$\alpha$	9	0.34047	3.89758	0.023	9.89805	9.96360	- 0.57367	0.19013	2.350	0.831
	14	0.17505	3.89826	0.014	9.82400	10.14663	- 0.62474	0.04615	2.349	- 1.950
	22	0.30768	3.89446	0.063	9.90882	9.95914	- 0.73991	0.12715	2.349	- 0.035
	34	0.31327	3.89614	0.019	9.87877	9.96638	- 0.52373	0.26868	2.350	1.784
	40	0.35728	3.89731	0.021	9.89219	9.96144	- 0.55927	0.23623	2.349	1.347
	52	0.33530	3.89702	0.027	9.89860	9.96481	- 0.54426	0.19782	2.350	1.039
$\beta$	9	0.31038	3.89352	0.082	9.91755	9.94928	- 0.62624	0.13301	2.360	1.000
	14	0.38179	3.89881	0.033	9.90224	9.95851	- 0.57609	0.17513	2.352	1.000
	22	0.34095	3.89848	0.052	9.89348	9.95316	- 0.57848	0.18922	2.338	0.999
	34	0.16612	3.89537	0.028	9.80857	10.0490	- 0.44888	0.12520	2.382	1.001
	40	0.35606	3.90903	0.019	9.88940	9.94183	- 0.61022	0.17903	2.329	1.001
	52	0.31834	3.89857	0.073	9.91742	9.93856	- 0.61263	0.12154	2.350	1.000

 

 

Table A.3: AMORE with one of the parameters fixed at one sigma from its original value. These tests provide an indication about the influence of one parameter on the retrieval of the remaining parameters. In particular, how the remaining parameters balance this mis-match by moving away from their optimal value. See Sects. 4.3.4 and 5.4 for additional details.

parameter	offset	model	$f_{\rm A}$	log d	$A_{\rm V}$	$\log t_{\rm low}$	$\log t_{\rm high}$	$[Z]_{\rm low}$	$[Z]_{\rm high}$	$\alpha$	$\beta$
log d	$-1\sigma$	9	0.21045	3.90307	0.008	9.70661	9.95123	- 0.54348	0.59806	2.318	4.573
		14	0.29182	3.90307	0.005	9.92758	9.95781	- 0.64641	0.10745	2.368	0.062
		22	0.30663	3.90307	0.055	9.90867	9.93700	- 0.62003	0.13004	2.332	0.373
		34	0.27406	3.90307	0.009	9.93190	9.95224	- 0.64172	0.09083	2.376	0.329
		40	0.30508	3.90307	0.031	9.88057	9.94765	- 0.56412	0.23885	2.330	1.482
		52	0.35736	3.90307	0.051	9.89002	9.94201	- 0.61187	0.18455	2.331	1.072
	$+1\sigma$	9	0.29273	3.90960	0.028	9.90776	9.93160	- 0.64116	0.10185	2.333	0.378
		14	0.33350	3.90960	0.007	9.89160	9.94261	- 0.62176	0.20013	2.336	1.201
		22	0.29174	3.90960	0.017	9.90814	9.94062	- 0.63653	0.11803	2.337	0.279
		34	0.15593	3.90960	0.000	9.82433	10.13280	- 0.74638	0.00763	2.346	- 1.894
		40	0.33700	3.90960	0.008	9.89589	9.94669	- 0.60483	0.15343	2.335	0.771
		52	0.26929	3.90960	0.032	9.91164	9.93459	- 0.64348	0.07215	2.340	0.145
$A_{\rm V}$	$+1\sigma$	9	-	-	-	-	-	-	-	-	-
		14	0.27049	3.89442	0.014	9.79866	9.96608	- 0.52682	0.49361	2.358	4.064
		22	0.28352	3.89378	0.014	9.87464	9.97332	- 0.55944	0.30339	2.359	1.855
		34	0.28608	3.89345	0.014	9.88671	9.97642	- 0.54707	0.30071	2.376	1.973
		40	0.26382	3.89346	0.014	9.81948	9.96660	- 0.52576	0.46184	2.358	3.610
		52	0.31545	3.89363	0.014	9.90003	9.97313	- 0.56649	0.23400	2.372	1.349
log $t_{\rm low}$	$-1\sigma$	9	0.27236	3.90040	0.040	9.85386	9.94757	- 0.55836	0.30935	2.323	1.896
		14	0.27545	3.89466	0.019	9.85386	9.97024	- 0.52819	0.37310	2.368	2.888
		22	0.27529	3.89648	0.018	9.85386	9.96558	- 0.54638	0.35495	2.350	2.384
		34	0.16883	3.89375	0.029	9.85386	10.08302	- 0.47457	0.01306	2.400	- 0.280
		40	0.28900	3.89953	0.033	9.85386	9.95405	- 0.56448	0.30320	2.324	1.779
		52	0.26942	3.89372	0.047	9.85386	9.96388	- 0.55833	0.34280	2.356	2.939
	$+1\sigma$	9	0.26839	3.89058	0.041	9.95232	9.95626	- 0.54291	0.11856	2.399	0.517
		14	0.27352	3.88923	0.037	9.95232	9.96263	- 0.68969	0.08041	2.401	- 0.347
		22	0.27555	3.88867	0.037	9.95232	9.95915	- 0.59030	0.06926	2.399	- 0.175
		34	0.29222	3.88687	0.054	9.95232	9.95543	- 0.60299	0.07026	2.398	- 0.115
		40	0.26972	3.88983	0.045	9.95232	9.95314	- 0.61176	0.08503	2.400	0.007
		52	0.29660	3.89064	0.046	9.95232	9.95592	- 0.65754	0.08096	2.401	0.003
log $t_{\rm high}$	$-1\sigma$	9	0.21567	3.90212	0.093	9.90420	9.90749	- 0.59379	0.10497	2.306	0.206
		14	0.25127	3.90319	0.111	9.90723	9.90749	- 0.68463	0.09099	2.318	0.272
		22	0.23271	3.90019	0.114	9.90634	9.90749	- 0.69157	0.08733	2.316	0.167
		34	0.24395	3.90526	0.113	9.89882	9.90749	- 0.64179	0.09370	2.307	0.470
		40	0.23796	3.90273	0.106	9.90270	9.90750	- 0.63701	0.10850	2.306	0.378
		52	0.19091	3.90474	0.105	9.85263	9.90750	- 0.54484	0.26544	2.274	2.304
	$+1\sigma$	9	0.18966	3.88133	- 0.001	9.84694	10.00986	- 0.51375	0.40765	2.432	3.306
		14	0.22621	3.88298	- 0.001	9.91537	10.00986	- 0.50616	0.26567	2.437	2.059
		22	0.21599	3.88275	0.000	9.73977	10.00986	- 0.51424	0.51570	2.413	4.449
		34	0.20975	3.88419	- 0.001	9.91194	10.00985	- 0.51870	0.26155	2.427	2.046
		40	0.19191	3.88460	0.013	9.79535	10.00985	- 0.52199	0.43616	2.405	3.653
		52	0.21132	3.88557	0.002	9.90671	10.00987	- 0.51864	0.27274	2.422	2.044
log $[Z]_{\rm low}$	$-1\sigma$	9	0.32236	3.89424	0.060	9.92490	9.94949	- 0.65235	0.09935	2.364	0.023
		14	0.19541	3.89205	0.085	9.80620	9.95304	- 0.65235	0.44787	2.367	4.219
		22	0.19646	3.89803	0.068	9.80556	9.95382	- 0.65235	0.48659	2.368	4.525
		34	0.19203	3.89730	0.066	9.76582	9.94810	- 0.65235	0.48742	2.316	4.023
		40	0.32867	3.89484	0.038	9.90919	9.95602	- 0.65235	0.18180	2.356	0.601
		52	0.28939	3.89843	0.035	9.88752	9.95511	- 0.65235	0.22274	2.337	0.836
	$+1\sigma$	9	0.30963	3.89302	0.019	9.89547	9.97009	- 0.55177	0.26207	2.372	1.833
		14	0.32883	3.89295	0.022	9.91000	9.97315	- 0.55177	0.19130	2.365	0.778
		22	0.32293	3.89110	0.024	9.91831	9.96435	- 0.55177	0.18106	2.369	0.671
		34	0.26376	3.89625	0.024	9.86434	9.96369	- 0.55177	0.37255	2.361	2.928
		40	0.33593	3.89840	0.032	9.90057	9.96348	- 0.55177	0.17853	2.349	0.885
		52	0.32988	3.89341	0.033	9.90827	9.97162	- 0.55177	0.20534	2.376	1.416
log $[Z]_{\rm high}$	$-1\sigma$	9	0.29612	3.89604	0.077	9.92807	9.93582	- 0.66338	0.04239	2.356	- 0.232
		14	0.29094	3.89708	0.082	9.92897	9.93400	- 0.67421	0.04239	2.359	- 0.139
		22	0.27692	3.89364	0.066	9.94038	9.95069	- 0.66032	0.04239	2.387	- 0.337
		34	0.28980	3.89736	0.083	9.92808	9.93087	- 0.63329	0.04239	2.357	- 0.095
		40	0.16160	3.90196	0.043	9.82928	10.10576	- 0.79270	0.04238	2.333	- 1.676
		52	0.30348	3.89643	0.078	9.92740	9.93508	- 0.66677	0.04239	2.355	- 0.238
	$+1\sigma$	9	0.26702	3.88982	0.031	9.88500	9.97615	- 0.56217	0.30979	2.384	2.280
		14	0.29357	3.89392	0.012	9.88192	9.97494	- 0.53776	0.30979	2.371	2.129
		22	0.30635	3.89366	0.032	9.87176	9.96383	- 0.53473	0.30979	2.351	2.194
		34	0.25823	3.89389	0.046	9.87585	9.96245	- 0.53400	0.30979	2.357	2.578
		40	0.28417	3.89886	0.028	9.85863	9.95559	- 0.57966	0.30979	2.333	1.926
		52	0.28883	3.89501	0.020	9.88098	9.96677	- 0.55136	0.30979	2.367	2.284
$\alpha$	$-1\sigma$	9	0.24524	3.90004	0.053	9.85726	9.94126	- 0.56638	0.28025	2.316	1.932
		14	0.28147	3.90272	0.020	9.87188	9.94707	- 0.54698	0.24944	2.316	1.230
		22	0.27797	3.89896	0.042	9.86368	9.94580	- 0.54982	0.26102	2.316	1.511
		34	0.22427	3.89644	0.032	9.82350	9.94534	- 0.50532	0.45532	2.316	3.679
		40	0.27857	3.90056	0.042	9.86375	9.94608	- 0.59271	0.26364	2.316	1.294
		52	0.28640	3.90139	0.039	9.85871	9.94768	- 0.58962	0.27721	2.316	1.438
	$+1\sigma$	9	0.23946	3.89295	0.062	9.87606	9.96018	- 0.57093	0.35127	2.384	3.499
		14	0.25586	3.89172	0.014	9.86873	9.97973	- 0.53518	0.35320	2.384	2.919
		22	0.28357	3.89109	0.021	9.91357	9.97110	- 0.56888	0.24524	2.384	1.488
		34	0.29934	3.89146	0.023	9.91497	9.97387	- 0.58765	0.23086	2.384	1.461
		40	0.25505	3.89153	0.009	9.80529	9.97968	- 0.52454	0.51555	2.384	4.820
		52	0.30437	3.89128	0.026	9.90426	9.97836	- 0.55141	0.23875	2.384	1.620

 

Table A.3: continued.

parameter	offset	model	$f_{\rm A}$	log d	$A_{\rm V}$	$\log t_{\rm low}$	$\log t_{\rm high}$	$[Z]_{\rm low}$	$[Z]_{\rm high}$	$\alpha$	$\beta$
$\beta$	$-1\sigma$	9	0.29110	3.89717	0.083	9.93098	9.93961	- 0.68243	0.02188	2.365	- 0.397
		14	0.17266	3.89314	0.001	9.83767	10.08181	- 0.41912	0.06629	2.372	- 0.397
		22	0.30211	3.89619	0.084	9.91729	9.94002	- 0.68522	0.06730	2.348	- 0.397
		34	0.16366	3.89491	0.015	9.81889	10.08661	- 0.50001	0.09684	2.363	- 0.397
		40	0.16472	3.89974	0.018	9.80958	10.07264	- 0.54158	0.11992	2.357	- 0.397
		52	0.29684	3.89592	0.074	9.91808	9.93138	- 0.66681	0.08493	2.339	- 0.397
	$+1\sigma$	9	0.26953	3.89638	0.045	9.86719	9.95699	- 0.57054	0.30738	2.346	2.397
		14	0.29111	3.89398	0.023	9.87948	9.97371	- 0.54141	0.30286	2.371	2.397
		22	0.28842	3.89548	0.029	9.86193	9.95692	- 0.53941	0.33240	2.341	2.397
		34	0.27336	3.89607	0.048	9.88719	9.95851	- 0.56455	0.27131	2.355	2.397
		40	0.26195	3.89766	0.038	9.87053	9.94793	- 0.58042	0.30908	2.345	2.397
		52	0.27328	3.89034	0.022	9.87427	9.97430	- 0.54963	0.33427	2.375	2.397