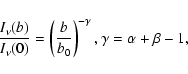 |
(5) |
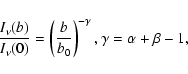 |
(5) |
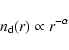 |
(6) |
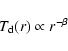 |
(7) |
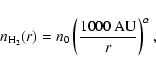 |
(8) |
To find the best fit model in the 3D parameter space the strategy
adopted is to first analyze the model grid by applying the observed
radial brightness distributions. As shown in Fig. 2, the
450 ![]() m and 850
m and 850 ![]() m brightness distributions are sensitive to
the slope of the density distribution and, to a lesser extent, the
size of the dusty envelope. Changing the total amount of dust by
changing
m brightness distributions are sensitive to
the slope of the density distribution and, to a lesser extent, the
size of the dusty envelope. Changing the total amount of dust by
changing
![]() has only a minor effect on the allowed values of
has only a minor effect on the allowed values of
![]() since normalized radial brightness distributions are used.
Values of
since normalized radial brightness distributions are used.
Values of ![]() in the range 1.5-1.9 are found to be acceptable,
with a preferred value of 1.7. A typical accuracy of
in the range 1.5-1.9 are found to be acceptable,
with a preferred value of 1.7. A typical accuracy of ![]() 0.2 in the
derived value of
0.2 in the
derived value of ![]() was also found by Jørgensen et al. (2002) when
analyzing SCUBA images at 450
was also found by Jørgensen et al. (2002) when
analyzing SCUBA images at 450 ![]() m and 850
m and 850 ![]() m for a large
sample of protostars. In general, the 450
m for a large
sample of protostars. In general, the 450 ![]() m data should provide
a more reliable value of
m data should provide
a more reliable value of ![]() because of the higher resolution, which
provides a larger sensitivity to changes in the density structure.
because of the higher resolution, which
provides a larger sensitivity to changes in the density structure.
The SED provides a good constraint on ![]() once the density profile
is known (Fig. 2; see also Doty & Palotti 2002).
For a density slope of 1.7 the optical
depth at 100
once the density profile
is known (Fig. 2; see also Doty & Palotti 2002).
For a density slope of 1.7 the optical
depth at 100 ![]() m is estimated to be approximately 4.5. At
450
m is estimated to be approximately 4.5. At
450 ![]() m and 850
m and 850 ![]() m the optical depths are
m the optical depths are ![]() 0.4 and
0.4 and
![]() 0.1 respectively.
For
0.1 respectively.
For
![]() the size of the envelope is not well constrained
which is not surprising given that only points in the brightness
distributions out to 50
the size of the envelope is not well constrained
which is not surprising given that only points in the brightness
distributions out to 50![]() (
(
![]() )
are used.
The circumstellar envelope will eventually merge with the more extended cloud material in which
the object is embedded. The maximum outer radius of the envelope is fixed at the point where
the dust temperature reaches 10 K.
The envelope size
)
are used.
The circumstellar envelope will eventually merge with the more extended cloud material in which
the object is embedded. The maximum outer radius of the envelope is fixed at the point where
the dust temperature reaches 10 K.
The envelope size
![]() is estimated to be
250 for the adopted
is estimated to be
250 for the adopted ![]() of 1.7.
of 1.7.
The quality of the best fit model can be judged from the reduced ![]() obtained from
obtained from
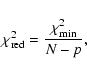 |
(9) |
Although disk emission is typically only responsible for a small fraction of the
total flux at sub-millimetre wavelengths it can contribute to the fluxes of the innermost
points on the brightness profiles leading to a steeper inferred density profile.
Tests in which the flux within a radius of one beam was reduced by 50%
indicate that the best fit value of ![]() is reduced by 0.1-0.2.
is reduced by 0.1-0.2.
The temperature and density structures obtained from the best fit model are
presented in Fig. 5. For comparison, the predicted temperature
structure based upon an optically thin approximation
(Chandler & Richer 2000) and scaled to the luminosity of IRAS 16293-2422 is shown for two different opacity laws.
Both predict the dust temperature to follow a single power-law.
Clearly, the temperature structure obtained from the detailed
radiative transfer analysis is not well described by a
power-law and has a significantly steeper gradient in the inner parts
of the envelope where optical depth effects are important.
The interstellar radiation field is potentially important for the
temperature structure in the outer parts of the envelope. However,
detailed modelling (S. Doty, priv. comm.) shows, for the envelope
around IRAS 16293-2422, that this effect is small when
assuming a typical interstellar radiation field. The difference in
the dust temperature is ![]() 10-20% (a few K) at
10-20% (a few K) at
![]() cm.
cm.
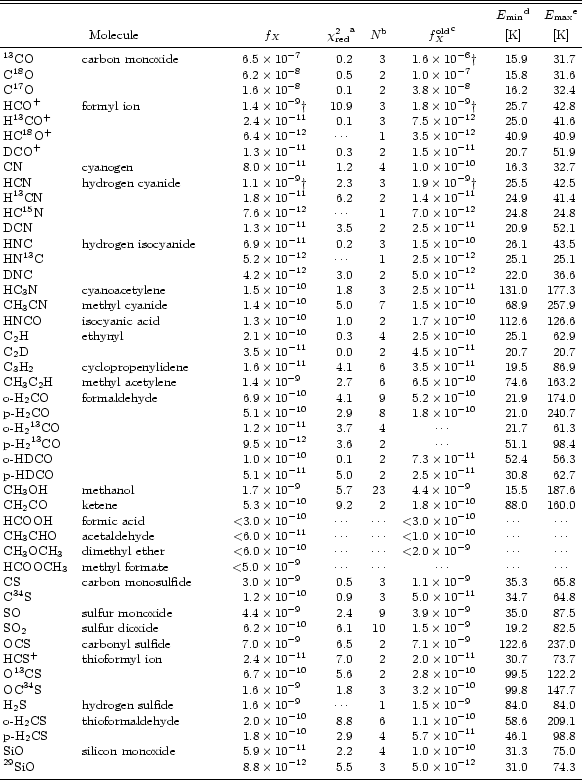
In addition to the analysis of the continuum emission the observed molecular
line emission is useful in constraining the physical properties of the envelope.
Traditionally, CO and CS line emission have been extensively used for this purpose and are
adopted here to test the validity of the best fit model obtained from the dust analysis.
Using the radiative transfer code presented in Sect. 3.2, the total CO and CS
abundances relative to H2 obtained for the best fit model presented in Table 4
are
![]() and
and
![]() ,
respectively.
In the
,
respectively.
In the ![]() -analysis only the velocity-integrated intensities in the lines were used.
These values are within a factor of about two of what is commonly derived for YSOs
(van der Tak et al. 2000b). The abundances in combination with the quality of the fits
(Fig. 4; see also Sect. 5),
in particular the ratios among various transitions which
are sensitive to the gas temperature and density, are reassuring and further strengthen the adopted
physical model.
-analysis only the velocity-integrated intensities in the lines were used.
These values are within a factor of about two of what is commonly derived for YSOs
(van der Tak et al. 2000b). The abundances in combination with the quality of the fits
(Fig. 4; see also Sect. 5),
in particular the ratios among various transitions which
are sensitive to the gas temperature and density, are reassuring and further strengthen the adopted
physical model.
In the modelling of the molecular line emission
the gas temperature is assumed to follow that of the dust.
In models which self-consistently treat
the energy balance the gas temperature is generally lower than that of the dust
in the outer regions due to imperfect gas-grain coupling
(Ceccarelli et al. 1996; Doty & Neufeld 1997; Ceccarelli et al. 2000a).
To test the effects of a departure of the gas temperature from that of
the dust due to gas-grain decoupling in the outer regions,
the dust temperature was scaled by a constant factor. For
![]() the
envelope becomes too cool to fit the observed line intensity
ratios. Thus, the gas temperature appears to follow that of the dust
within
the
envelope becomes too cool to fit the observed line intensity
ratios. Thus, the gas temperature appears to follow that of the dust
within ![]() 30% in the region probed by the CO emission.
30% in the region probed by the CO emission.
The static envelope model fails to explain the details of the
individual spectra and the potential of the molecular emission to constrain the velocity fields will
be investigated further in Sect. 4.3.
The derived abundances are not very sensitive to the adopted value of ![]() ,
within the
limits derived from the dust radiative transfer model. Similarly, increasing the outer radius by a factor
of two only marginally affects the line intensities.
The abundances derived
for a wide variety of molecular species are further presented in Sect. 5.
,
within the
limits derived from the dust radiative transfer model. Similarly, increasing the outer radius by a factor
of two only marginally affects the line intensities.
The abundances derived
for a wide variety of molecular species are further presented in Sect. 5.
Thus, the emerging picture from the analysis is that the envelope around
IRAS 16293-2422 indeed has a region of dense and hot gas
inside a radius of
![]() cm (150 AU, 1
cm (150 AU, 1![]() ),
with temperatures decreasing to
),
with temperatures decreasing to ![]() 10 K at
10 K at ![]() 1017 cm
(8000 AU).
1017 cm
(8000 AU).
| |
Figure 5:
Properties of the circumstellar envelope around IRAS 16293-2422 obtained from the
dust modelling. Shown are the dust temperature (left) and density (middle) structures
for best fit model (full line) assuming a single power-law distribution of the density.
In the temperature panel, an optically thin prediction using an opacity
law
|
In the Shu inside-out collapse model the self-similar solution is
presented in terms of the dimensionless variable x = r/at, where ris the radial distance scale, and characterized by the isothermal
speed of sound, a, and the time after onset of collapse, t. The
location of the collapsing wave front at any instant t is described
by
![]() .
The density
.
The density ![]() and velocity u have
the form
and velocity u have
the form
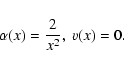 |
(11) |
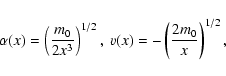 |
(12) |
The input parameters to DUSTY are the same as for the single power-law
models (see Table 4). In addition, the envelope size was
fixed to a radius 5000 AU. Making the envelope larger will produce
increasingly worse fits to the radial brightness distributions obtained
from the SCUBA observations. The sensitivity of the two adjustable
parameters a and
![]() in the modelling is shown in
Fig. 6 (left panel)
where the observational constraints used are the
SED and the SCUBA 450
in the modelling is shown in
Fig. 6 (left panel)
where the observational constraints used are the
SED and the SCUBA 450 ![]() m radial brightness distribution. The
best fit model is obtained using
m radial brightness distribution. The
best fit model is obtained using ![]() km s-1 and
km s-1 and
![]() cm, putting the age at
cm, putting the age at ![]() 104 yr.
104 yr.
The mass accretion rate can be estimated from
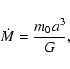 |
(13) |
The relative success of the dust modelling using a static envelope,
with a single power-law to describe the density structure, makes it
hard to discriminate between the two models in the present
analysis. In Fig. 5 the density and velocity structures
obtained from the best fit Shu model are presented and, for the
density, compared with results from the static envelope model.
The largest discrepancy
occurs at small radial distances where the collapsing envelope model
predicts about a factor of two to three lower densities. We stress
the observational data set used in the dust modelling is not directly probing this region.
At larger radii the model is better constrained and the two models agree well.
It should be noted that the best fit single power-law model
gives slightly better reduced ![]() values for the combined set of
observations. However, the molecular data provide further constraints
since they have the potential to probe the large scale velocity field.
values for the combined set of
observations. However, the molecular data provide further constraints
since they have the potential to probe the large scale velocity field.
In Fig. 4, spectra of CO and CS line emission as observed with the JCMT are presented.
Lines which are optically thick, like CS, 13CO and C18O (
![]() ),
show a distinct, narrow, absorption feature near the stellar velocity. This feature is due to effective
self-absorption in the outer cool parts of the envelope.
Also, the degree of the asymmetry in the line profiles
increases with the optical depth in the lines. In the optically thin lines the self-absorption feature
disappears and the lines are well described by a single Gaussian profile.
The width of the self-absorption
feature constrains the turbulent velocity to
),
show a distinct, narrow, absorption feature near the stellar velocity. This feature is due to effective
self-absorption in the outer cool parts of the envelope.
Also, the degree of the asymmetry in the line profiles
increases with the optical depth in the lines. In the optically thin lines the self-absorption feature
disappears and the lines are well described by a single Gaussian profile.
The width of the self-absorption
feature constrains the turbulent velocity to ![]() 0.3 km s-1 in the outer envelope. For
simplicity this value is adopted throughout the envelope. A turbulent velocity component
varying with radius is beyond the scope of this article,
see however Stark et al. (2002, in prep.).
0.3 km s-1 in the outer envelope. For
simplicity this value is adopted throughout the envelope. A turbulent velocity component
varying with radius is beyond the scope of this article,
see however Stark et al. (2002, in prep.).
The observed CS emission (including that from C34S) is analyzed
using the abundances derived from the static envelope model
presented in Sect. 4.2 (see also Sect. 5).
From only the integrated intensities it is possible to
constrain both a and ![]() as is shown in
Fig. 6 (middle panel).
The model spectra are presented in Fig. 4 together with
the observations. The fit to the integrated intensities is worse than that
obtained from the single power-law model presented in
Sect. 4.2, however. In particular the
C34S (
as is shown in
Fig. 6 (middle panel).
The model spectra are presented in Fig. 4 together with
the observations. The fit to the integrated intensities is worse than that
obtained from the single power-law model presented in
Sect. 4.2, however. In particular the
C34S (
![]() )
line is poorly reproduced in the
infall model.
Using also the line profiles as constraints we find
that a model where the collapsing wavefront is located at
)
line is poorly reproduced in the
infall model.
Using also the line profiles as constraints we find
that a model where the collapsing wavefront is located at
![]()
![]() cm and the value of a is
cm and the value of a is
![]() 0.9 km s-1 best reproduces the observations.
0.9 km s-1 best reproduces the observations.
Analyzing the CO emission (13CO, C18O, and C17O) gives
yet another set of estimates. At first the abundances derived from the static envelope
models presented in Sect. 4.2 (see also Sect. 5) are adopted.
From the analysis of the integrated intensities shown in Fig. 6 (right panel)
and the line profiles presented in Fig. 4
a Shu-model with ![]() km s-1 and
km s-1 and
![]() cm reproduces the CO observations well,
in excellent agreement with the CS modelling.
The derived dynamical age of the system is
cm reproduces the CO observations well,
in excellent agreement with the CS modelling.
The derived dynamical age of the system is
![]() yr.
In contrast with the CS modelling, the fit to the integrated CO intensities
is equally good as obtained for the single power-law model.
As discussed in Sect. 5, the CO abundance obtained from the static envelope
model is about a factor of 2-3 lower than what is typically observed for interstellar gas.
If instead the CO abundance relative to H2 is
assumed to be the "standard'' interstellar value of
yr.
In contrast with the CS modelling, the fit to the integrated CO intensities
is equally good as obtained for the single power-law model.
As discussed in Sect. 5, the CO abundance obtained from the static envelope
model is about a factor of 2-3 lower than what is typically observed for interstellar gas.
If instead the CO abundance relative to H2 is
assumed to be the "standard'' interstellar value of
![]() and the standard isotopic ratios are assumed ([CO/13CO] =60, [CO/C17O] =2500, and
[C18O/C17O] =3.9) the estimate
of a is
and the standard isotopic ratios are assumed ([CO/13CO] =60, [CO/C17O] =2500, and
[C18O/C17O] =3.9) the estimate
of a is ![]() 0.75 and
0.75 and
![]() cm. However, the quality of the fit becomes worse in this case.
cm. However, the quality of the fit becomes worse in this case.
The results obtained from the best fit Shu-model are presented in Fig. 4 overlayed onto the observed CO and CS spectra. The integrated intensities and, to some extent, line profiles can be modelled with the spherically symmetric infall solution. The details of the spectra will, however, intricately depend on the adopted geometry, velocity fields, and chemical gradients. The velocity field, in particular position-velocity maps of the source, form a stringent test of the dynamical models. For IRAS 16293-2422 it will likely be necessary to include a rotational component to the velocity field (Menten et al. 1987; Zhou 1995; Narayanan et al. 1998).
Other estimates of the infall radius, based on analysis of molecular
line emission, range between about 5 and
![]() cm
(Walker et al. 1986; Zhou 1995; Narayanan et al. 1998; Ceccarelli et al. 2000a) in excellent
agreement with the values obtained here from analysis of CO and CS
emission. However, there appears to be a discrepancy between the dust
and molecular line analysis, possibly reflecting the fact that the
simple Shu-collapsing core model is not fully adequate to describe the
state of the infalling material and/or that some of the CO and CS
emission is associated with the outflow and surrounding
cloud. Moreover, gradients in the molecular abundances will affect the
parameters derived.
cm
(Walker et al. 1986; Zhou 1995; Narayanan et al. 1998; Ceccarelli et al. 2000a) in excellent
agreement with the values obtained here from analysis of CO and CS
emission. However, there appears to be a discrepancy between the dust
and molecular line analysis, possibly reflecting the fact that the
simple Shu-collapsing core model is not fully adequate to describe the
state of the infalling material and/or that some of the CO and CS
emission is associated with the outflow and surrounding
cloud. Moreover, gradients in the molecular abundances will affect the
parameters derived.
Copyright ESO 2002