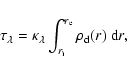 |
(1) |
The most important parameter controlling the output is the dust optical depth
The dust temperature at the inner radius of the envelope is fixed to
300 K and this sets the inner radius. The choice of this temperature
is motivated by the observations of line emission arising from highly
excited molecules in the envelope. However, the inner regions are
complex with breakdown of spherical symmetry and interactions between
disk, envelope and outflow. In the present analysis these
complications are ignored and for simplicity a smooth and
spherically-symmetric envelope is assumed. Recently,
Ceccarelli et al. (2000a) successfully modelled molecular line emission in
the envelope around IRAS 16293-2422 down to ![]() 30 AU,
assuming spherical symmetry.
While the separation of the two protostars
is approximately 800 AU (Looney et al. 2000), one of the protostars
IRAS 16293A (MM1) exhibits jet-like centimetre
wavelength emission, water maser emission and associated millimetre
molecular emission, thus appearing to be significantly more active
(Wootten & Loren 1987; Mundy et al. 1992;
Schöier et al. 2002a, in prep.), which justifies the approach
taken here. The central source of radiation is assumed to arise from
a blackbody at 5000 K. This is an oversimplification considering the
binary nature of IRAS 16293-2422 and the uncertainty in the
intrinsic SED of a protostar. The final model does not depend on
the exact stellar temperature adopted, however, within a reasonable
range of values, since the radiation is totally reprocessed by the
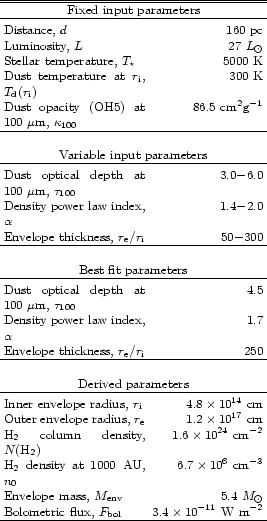
circumstellar dust. The input parameters are summarized in
Table 4.
30 AU,
assuming spherical symmetry.
While the separation of the two protostars
is approximately 800 AU (Looney et al. 2000), one of the protostars
IRAS 16293A (MM1) exhibits jet-like centimetre
wavelength emission, water maser emission and associated millimetre
molecular emission, thus appearing to be significantly more active
(Wootten & Loren 1987; Mundy et al. 1992;
Schöier et al. 2002a, in prep.), which justifies the approach
taken here. The central source of radiation is assumed to arise from
a blackbody at 5000 K. This is an oversimplification considering the
binary nature of IRAS 16293-2422 and the uncertainty in the
intrinsic SED of a protostar. The final model does not depend on
the exact stellar temperature adopted, however, within a reasonable
range of values, since the radiation is totally reprocessed by the
circumstellar dust. The input parameters are summarized in
Table 4.
The observational constraints, as presented in
Sect. 2, are the SED and radial brightness
distributions at 450 ![]() m and, to a lesser extent, 850
m and, to a lesser extent, 850 ![]() m.
The ability of the model to reproduce the observational constraints
are quantified using the chi-squared statistic
m.
The ability of the model to reproduce the observational constraints
are quantified using the chi-squared statistic
 |
Adopting the parameters of the circumstellar envelope derived from the dust radiative transfer analysis, the Monte Carlo code calculates the steady-state level populations of the molecule under study, using the statistical equilibrium equations. In the Monte Carlo method, information on the radiation field is obtained by simulating the line photons using a number of model photons, each representing a large number of real photons from all transitions considered. These model photons, emitted locally in the gas as well as injected from the boundaries of the envelope, are followed through the envelope and the number of absorptions are calculated and stored. Photons are spontaneously emitted in the gas with complete angular and frequency redistribution, i.e., the local emission is assumed to be isotropic and the scatterings are assumed to be incoherent. The weight of a model photon is continuously modified as it travels through the envelope, to take the absorptions and stimulated emissions into account. When all model photons are absorbed in, or have escaped from, the envelope the statistical equilibrium equations are solved and the whole process is then repeated until some criterion for convergence is fulfilled. Once the molecular excitation, i.e., the level populations, is obtained the radiative transfer equation can be solved exactly. The resulting brightness distribution is then convolved with the appropriate beam to allow a direct comparison with observations. In this analysis, the kinetic temperature of the gas is assumed to follow that of the dust (Ceccarelli et al. 1996; Doty & Neufeld 1997; Ceccarelli et al. 2000a).
Typically, energy levels up to ![]() 500 K in the
ground vibrational state were retained in the analysis. Vibrationally
excited levels are not included since the radiative excitation
due to the dust is generally inefficient and,
for the temperature and
density ranges present here, collisional excitation to these levels is
negligible. Line emission from rotational transitions within
vibrationally excited states has, however, been observed for some
species (e.g., the CS (v =1,
500 K in the
ground vibrational state were retained in the analysis. Vibrationally
excited levels are not included since the radiative excitation
due to the dust is generally inefficient and,
for the temperature and
density ranges present here, collisional excitation to these levels is
negligible. Line emission from rotational transitions within
vibrationally excited states has, however, been observed for some
species (e.g., the CS (v =1,
![]() )
Blake et al. 1994). In Sect. 5 the nature of such
emission is discussed further. Collisional rate coefficients are taken from the
literature and, in the case of some linear molecules, extrapolated
both in temperature and to transitions involving energy levels with
higher J quantum numbers when needed (see Schöier et al. 2002b, in prep. for
details). For other (non-linear) species for which such extrapolations
are not obvious, the excitation is assumed to be in LTE for levels for
which no collisional rate coefficients are available.
)
Blake et al. 1994). In Sect. 5 the nature of such
emission is discussed further. Collisional rate coefficients are taken from the
literature and, in the case of some linear molecules, extrapolated
both in temperature and to transitions involving energy levels with
higher J quantum numbers when needed (see Schöier et al. 2002b, in prep. for
details). For other (non-linear) species for which such extrapolations
are not obvious, the excitation is assumed to be in LTE for levels for
which no collisional rate coefficients are available.
In what follows, all quoted abundances, ![]() ,
for a
particular molecular species X are relative to that of molecular
hydrogen, i.e.,
,
for a
particular molecular species X are relative to that of molecular
hydrogen, i.e.,
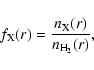 |
(4) |
The beam profile used in the convolution of the modelled emission is
assumed to be Gaussian which is appropriate at the frequencies used
here. The best fit model is estimated from the ![]() -statistic
defined in Eq. (3) using the observed integrated
intensities and assuming a 30% calibration uncertainty. Even though
the new data presented in Table 3 appear to be slightly
better calibrated, the old data set constitutes the vast majority of
observational constraints so the larger calibration uncertainty is
applied to the full data set, for simplicity. Only in the cases of
CO and CS was a lower calibration uncertainty
of 15% adopted. These molecules are regularly observed towards
IRAS 16293-2422 and used as standard spectra.
-statistic
defined in Eq. (3) using the observed integrated
intensities and assuming a 30% calibration uncertainty. Even though
the new data presented in Table 3 appear to be slightly
better calibrated, the old data set constitutes the vast majority of
observational constraints so the larger calibration uncertainty is
applied to the full data set, for simplicity. Only in the cases of
CO and CS was a lower calibration uncertainty
of 15% adopted. These molecules are regularly observed towards
IRAS 16293-2422 and used as standard spectra.
Copyright ESO 2002