5 Molecular abundances

The basic envelope parameters derived from the dust radiative transfer modelling performed in Sect. 4, in particular the density and temperature distributions, are used as input for the Monte Carlo modelling of the molecular line emission. The static power-law model is adopted; the abundances obtained with the best fitting infall model generally differ by no more than $\sim$25% for a constant abundance model. However, models where a drastic enhancement in the abundance is introduced ("jump-models'') require 2-3 times larger abundances in the inner hot part for a Shu-type collapsing model, reflecting the significantly lower density compared to the static power-law model in this region (Fig. 5). Changing the envelope parameters describing the static power-law model within the accepted range of values (Fig. 2) typically affects the abundances obtained for the best fit model by less than $\pm$25% for constant abundance models. In "jump-models'' the effect on lines which are sensitive to the conditions in the innermost dense and hot regions can be higher, up to $\pm$50%.

5.1 Constant abundance models

The abundances are initially assumed to be constant throughout the envelope. For simplicity the observed lines are assumed to be broadened (in addition to thermal line broadening) by microturbulent motions only. The microturbulent velocity is set equal to 2 km s^-1 throughout the envelope typically producing lines $\sim$4 km s^-1 (FWHM) wide (see Sect. 6). The presence of a global velocity field, e.g., infall, outflow, or rotation, would serve to reduce the optical depths of the line emission, so that the abundances presented in Table 5 are strictly lower limits. However, such effects will not significantly increase the inferred abundances since they are largely derived from optically thin lines. The observational constraints used in the modelling are the total velocity-integrated line intensities.

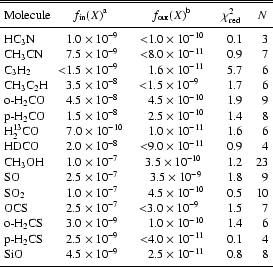
In many cases the observations are well reproduced assuming a constant abundance throughout the envelope, as seen from their reduced $\chi^2 \sim1$. In the cases where the fits are good the derived abundances are generally consistent with typical values found in quiescent molecular clouds. In addition, the isotopic ratios of ¹⁸O/ $^{17}\rm O\sim3.9$ determined from CO observations and ³²S/ $^{34}\rm S\sim25$ from CS observations, agree well with interstellar values (Wilson & Rood 1994). A notable exception is the relatively low abundance, $\sim$ $7\times10^{-11}$, derived for HNC. The abundances derived by Blake et al. (1994) and van Dishoeck et al. (1995) agree surprisingly well with the new, more accurate, estimates presented here (Table 5), typically within a factor of $\sim$2. Those abundances were derived from statistical equilibrium equations assuming a constant temperature and density. The agreement indicates that the adopted values were representative of the region from which most of the submillimetre emission arises.

For the main isotopes of HCN and HCO⁺ the emission is highly optically thick and the models are relatively insensitive to the molecular abundance. The abundances of these molecules were instead estimated from the rarer isotopomers assuming a standard isotope ratio, i.e., ¹²C/ $^{13}\rm C=60$. The abundances obtained in this way fail to account for all of the observed flux in the HCN and HCO⁺ lines, as evidenced by their high reduced $\chi ^2$-values in Table 5. Adopting the best fit Shu-infall model derived from CO and CS observations and presented in Sect. 4.3 introduces a large-scale velocity field which reduces the line optical depths and increases the line intensities thus improving the fit to observations. Material in the outflow can also contribute to these lines.

The observed transitions are only in LTE throughout the envelope for abundant molecules like CO and OCS, including their isotopomers observed here. For less abundant species, where collisional excitation is less efficient, departures from LTE are found. For example, the level populations of common molecules like CS and H₂CO are in LTE out to ${\sim}1{-}2\times10^{16}$ cm. For most molecules, populations of the observed lines are in LTE within ${\sim}2\times10^{15}$ cm.

From Table 5 it is also evident that the line emission from several molecular species is not fitted well, in particular molecules where the emission probes a large radial range, e.g., in the case of H₂CO and CH₃OH. In addition, the isotopic ratios derived in many of these cases are far from their interstellar values and what is commonly derived for these kind of objects. Typically, the model intensities from lines sampling the inner parts of the envelope are too low compared to observed values, whereas the opposite is true for the lines probing the outer part of the envelope. An obvious explanation is that a steep gradient is present in the abundances of these molecules.

   
5.2 Jump models

In order to improve the quality of the fits, models with a jump in the molecular abundances are considered. A jump is introduced at the radius in the envelope where the temperature reaches 90 K, at which point the ice starts to evaporate from the grain mantles. In our models, this occurs at ${\sim}2\times10^{15}$ cm or 150 AU. The free parameters in the modelling are then the fractional abundances in the inner ( $f_{{\rm in}}$; T>90 K) and outer parts of the envelope ( $f_{{\rm out}}$; T<90 K). For most species, the isotopic abundance ratios are assumed to be fixed to the standard interstellar values to increase the number of constraints used in the modelling. The results from the excitation analysis are presented in Fig. 7 for several species. The reduced $\chi ^2$ for the best fit models are generally very good, $\sim$1, and significantly better than the constant abundance models. Typically, a jump of $\sim$100 in abundance is derived, leading to abundances that are significantly higher than found in quiescent molecular clouds and comparable to those found in the prototypical hot core in Orion (Sect. 6).

The jump models can only be applied to species for which a significant number of lines are observed covering a wide range of excitation conditions. These include H₂CO, CH₃OH, CH₃CN, H₂CS, SO and SO₂ (see the columns of $E_{\rm max}$ and $E_{\rm min}$ included in Table 5). For HC₃N and OCS, only lines from highly-excited levels have been observed, so that for these molecules the values of $f_{{\rm out}}$in the outer envelope are poorly constrained. For most simple linear rotors such as HCN, HCO⁺, CN, however, the observed lines arise from levels below 90 K, so that no information on the inner warm part is obtained. The only exception is SiO, where the combination of many ²⁸SiO and ²⁹SiO lines allows a jump to be inferred. Molecules such as HNCO, CH₂CO and H₂S for which only one or two lines are observed and where the emission mainly probes hot gas (Table 5) only the inner part of the envelope were modelled. The significantly higher abundances obtained (Sect. 6) compared with the constant abundance models illustrates the point that orders of magnitude higher abundances can be derived if the emission is assumed to originate only from the inner warm region.

  

Table 6: Various molecular abundances derived using a jump in their fractional abundance, introduced at T = 90 K.

$^{\rm a}$ Abundance in the inner, dense, and hot part of the envelope.
   $^{\rm b}$ Abundance in the cooler, less dense, outer part of the envelope.

The observations analyzed in this paper do not include the lowest rotational transitions probing the coldest outer parts; thus, so-called "anti-jump'' models, in which the abundances are decreased below a certain temperature due to freeze-out, cannot be tested, except for the case of CO. There are also some molecules, e.g., C₃H₂, for which the jump-models give a worse $\chi ^2$-fit than the constant abundance models; such molecules are good candidates for the "anti-jump'' models if lower transitions are available. In the following, a few individual cases are described in more detail, before discussing the general results.

Figure 7: $\chi ^2$-maps of various molecular species introducing a step function in abundance at $T_{{\rm gas}}=90$ K. Contours are drawn at $\chi ^2_{{\rm min}}$+(2.3, 4.6, 6.2) indicating the 68%, 90%, and 95% confidence levels, respectively. The number of observational constraints used, N, are also shown. The quality of the best fit model can be estimated from the reduced chi-squared $\chi ^{2}_{{\rm red}} = \chi ^{2}_{{\rm min}}$/(N-2). Fixed isotope ratios of 28SiO/ $^{29}\rm SiO=20$, OCS/OC $^{34}\rm S=20$ and OCS/O $^{13}\rm CS=60$ were assumed.

5.3 CO

Carbon monoxide, CO, is difficult to destroy but relatively easy to excite through collisions, even in the outer low-density and cold part of the envelope. Brightness maps of the ¹²CO molecular line emission associated with IRAS 16293-2422 reveal a complex structure (Walker et al. 1988) indicating two bipolar outflows. Interferometric BIMA observations suggest that the ¹³CO ( $J = 1\rightarrow 0$) emission is also associated with the outflow to some extent (Schöier et al. 2002a, in prep.). Single-dish observations of higher transitions of ¹³CO show no direct evidence for tracing the outflow based upon the shape of their line profiles (see Fig. 4). This is also the case for lines from the less abundant C¹⁷O and C¹⁸O molecules. Thus these lines can possibly be used to trace the CO content in the circumstellar envelope.

Assuming a constant abundance throughout the envelope the radiative transfer calculations give abundances of $6.5\times10^{-7}$, $6.2\times10^{-8}$ and $1.6\times10^{-8}$ for ¹³CO, C¹⁸O, and C¹⁷O, respectively. The derived C¹⁸O/C¹⁷O ratio is 3.9, in good agreement with typical interstellar values (Wilson & Rood 1994). Jørgensen et al. (2002) derived ¹⁸O/ $^{17}\rm O=3.6\pm1.1$ for their survey of protostellar objects. The ¹²CO abundance is estimated to be $4.0\times10^{-5}$ from C¹⁷O assuming the terrestrial ratio ¹²CO/C $^{17}\rm O=2500$. This is in excellent agreement with the value of $3.9\times10^{-5}$ estimated from ¹³CO using the interstellar value ¹²CO/ $^{13}\rm CO=60$. In addition, the upper limits obtained for the ¹³C¹⁷O ( $J = 2\rightarrow 1$) and ¹³C¹⁸O ( $J = 3\rightarrow 2$) line emission are also consistent with these values. In all, the consistency of the derived values and quality of the model fits (Fig. 4 and Table 5) are reassuring. Due to the high optical depths in the observed ¹³CO lines, their profiles tend to be somewhat broader than those from the less abundant isotopomers, and their intensities are less sensitive to the assumed abundance. The observed lines are all in LTE, indicating that the derived abundances are not sensitive to the adopted set of collisional rates.

The total inferred CO abundance is about a factor of two to four lower than the value of $8\times 10^{-5}$ found in dark clouds (Frerking et al. 1982) and $2\times 10^{-4}$ in warm regions (Lacy et al. 1994). A plausible explanation is that CO freezes out in the cool external parts of the envelope. To simulate this situation, a "jump'' model with an abrupt decrease in the CO abundance at 20 K was introduced; this is a characteristic temperature below which pure-CO ice can exist (Sandford & Allamandola 1993). To compensate for this freeze-out, the CO abundance in regions above 20 K needs to be raised. In Fig. 8 the result of varying the CO abundance in the inner and outer parts of the envelope is presented. A maximum allowed value for the CO abundance of gas above 20 K is $\sim$ $7\times 10^{-5}$ while at the same time the abundance in the outer cooler envelope needs to be lowered to ${\la}2\times10^{-5}$, i.e., a depletion of about a factor four. However, in the present analysis a constant abundance model is equally probable. The molecular line modelling performed in Sect. 4.2 suggests that in the envelope around IRAS 16293-2422, $T_{{\rm gas}} \ga 0.7\times$ $T_{{\rm dust}}$. This in turn means that it is not possible to explain the apparently low CO abundance with a significant decoupling of the gas temperature from that of the dust.

For the similar modelling of the larger sample of class 0 and I objects, Jørgensen et al. (2002) found that the CO abundance in general was lower for the class 0 objects than the class I objects (average CO abundances of respectively $2.0\times 10^{-5}$ and $1.2\times 10^{-4}$). Further it was found that abundance jumps at 20 K of more than a factor 3 could be ruled out in most cases and that constant fractional abundances over the temperature range covered by the CO rotational lines provided good fits. This lead to the suggestion that CO in the class 0 objects could be trapped in a porous ice matrix with H₂O from which it does not fully evaporate until at temperatures of $\sim$60 K. More observational constraints on isotopic CO ( $J = 1\rightarrow 0$) as well as higher-J CO lines are needed to verify if CO is frozen out onto dust grains only at the lowest temperatures or if a substantial fraction of CO evaporates more gradually up to $\sim$90 K, as suggested by recent experiments of CO-H₂O ice mixtures (Collings et al. 2002).

In Fig. 4 the line profiles obtained from the constant abundance model of the CO emission are presented. The asymmetry present in some of the observed spectra is not possible to model using a static envelope and requires the presence of a global velocity field, as discussed in Sect. 4.3.

Figure 8: CO jump-model assuming an abrupt change in abundance at 20 K using the integrated intensities of the observed 13CO, C18O, and C17O line emission as constraints. Contours are drawn at $\chi ^2_{{\rm min}}$+(2.3, 4.6, 6.2) indicating the 68%, 90%, and 95% confidence levels, respectively. The number of observational constraints used, N, are also shown. The quality of the best fit model can be estimated from the reduced chi-squared $\chi ^{2}_{{\rm red}} = \chi ^{2}_{{\rm min}}$/(N-2).

5.4 H $_{\mathsfsl 2}$CO and CH $_{\mathsfsl 3}$OH

H₂CO and CH₃OH are two particularly useful molecules to model in detail, because of the relative complexity of the energy level structure of asymmetric rotors and symmetric top molecules. For example, for H₂CO dipole transitions between various K_p-ladders are not allowed while collisional transitions are, making these transitions good probes of the temperature structure. In addition, the wealth of available lines in the submillimetre regime makes them ideal to probe various parts of the envelope (Mangum & Wootten 1993; van Dishoeck et al. 1993; Ceccarelli et al. 2000b). It is clear from Table 6 that the reduced $\chi ^2$ values are considerably lowered in the jump-model for an abundance contrast of $\sim$60-100 for H₂CO and $\sim$50 for CH₃OH. The H₂CO and CH₃OH abundances in the cool outer part of the envelope are in line with values in quiescent molecular clouds, whereas those in the inner envelope are of the same order of magnitude as derived for some hot cores (Sect. 6). Typical CH₃OH and H₂CO abundances in interstellar ices are ${\la}2\times10^{-6}$ and $\sim$10^-6(Dartois et al. 1999; Keane et al. 2001), illustrating that the drastic increases could be explained by ice evaporation from dust grains above 90 K. For high-mass protostars, van der Tak et al. (2000a) found a similar CH₃OH abundance jump for some sources, but no evidence for significant jumps in the H₂CO abundance. The H₂CO/CH₃OH ice abundance ratio is sensitive to the atomic hydrogen density in the ice-forming region, which could be different for low- and high-mass protostars.

When a significant number of transitions with varying excitation conditions are observed the data have the potential to determine the characteristic temperature at which the majority of the molecules are evaporated. The sensitivity of the data presented here to the adopted jump-temperature can thus be tested for H₂CO and CH₃OH. The H₂CO models are not very sensitive to the jump temperature until it drops below about 40 K at which point the reduced $\chi ^2$ increases fast. It is found that a temperature of $\sim$50 K gives the best fit indicating that formaldehyde starts to evaporate at temperatures below 90 K (see also Ceccarelli et al. 2001). In the case of methanol (CH₃OH), the best fit is obtained for $\sim$90 K whereas temperatures below $\sim$50 K give poor fits, indicating that this molecule evaporates mainly at $\sim$90 K.

The ortho-to-para ratio of H₂CO is not well constrained. Based on the $\chi ^2$-analysis, its lower limit is $\sim$0.9, with a best-fit value of 2.5. A further complication is that the ortho-to-para ratio may vary, e.g. according to temperature, through the envelope. In the present analysis it is not possible to confirm this. Fixing the ortho-to-para ratio to 2.5 throughout the envelope increases the number of constraints used in the modelling and enables "jump-models'' for H₂¹³CO and HDCO to be inferred. From the isotopic ratio, the derived ¹²C/¹³C-ratio is $\sim$100 with considerable uncertainty and fully consistent with the interstellar value of 60 adopted elsewhere in this paper. From deuterated formaldehyde (HDCO) it is possible to estimate the D/H ratio and a value $\sim$0.3 is derived. This is significantly higher than what is obtained from DCO⁺/HCO⁺, DCN/HCN and DNC/HNC (see Table 5), and suggests a different scenario for H₂CO. The high degree of deuterium fractionation of H₂CO, further strengthened by the recent detection of D₂CO in this source (Loinard et al. 2000; Ceccarelli et al. 2001), is about five times larger than values obtained towards other low-mass protostars (Roberts et al. 2002) and dark clouds like TMC-1 and L134N (Turner 2001) but consistent with estimates for the Orion hot core (Turner 1990). Due to the limited number of lines any radial variations in either the ¹²C/¹³C-ratio or the deuterium fractionation cannot be established. Ceccarelli et al. (2001) argue, based on spatially resolved emission, that H₂CO and its deuterated counterparts are formed mainly from grain-surface reactions in a previous cold, dark cloud phase. For HCO⁺, HCN and HNC the degree of deuteration can be explained by gas-phase reactions at low temperatures (Roberts et al. 2002).

5.5 Vibrationally excited emission?

For linear rotors such as CS and HCN, the observed lines cover only a limited range in excitation energy. Much higher frequency data are needed to probe the abundances of these molecules in the warm gas through pure rotational lines in the vibrational ground state (e.g., Boonman et al. 2001). Some lines of vibrationally-excited molecules have been detected toward IRAS 16293-2422, however, in particular the CS (v = 1; $J =7\rightarrow 6$) line. Since this line originates from a level at about 1900 K above ground, it cannot be excited by collisions only. Instead, radiative excitation by dust emission must play a role.

The addition of radiative excitation by dust is straightforward in the Monte Carlo scheme if scattering is assumed to be negligible, which is the case at the wavelengths of importance here: the CS fundamental vibrational transition occurs around 8 $\mu$m. In the absence of scattering events only emission and absorption by the dust particles need to be considered. The dust is assumed to locally emit thermal radiation described by the dust temperature T(r), according to Kirchhoff's law. The model photons emitted by the dust are released together with the other model photons and the additional opacity provided by the dust is added to the line optical depth.

The CS abundance of $2.5\times 10^{-9}$ derived previously fails to account for the observed CS (v = 1; $J =7\rightarrow 6$) line emission by many orders of magnitudes. Even a "jump-model'' with the abundance increased by a factor of 100 fails to account for all the observed emission.

Recently, Highberger et al. (2000) failed to detect any vibrationally excited CS emission in lower J-transitions towards IRAS 16293-2422 down to $T_{{\rm rms}} \sim10$ mK. One possibility is that the CS (v = 1; $J =7\rightarrow 6$) line was mis-identified by Blake et al. (1994). Their observations were obtained in dual sideband and the CS line was supposed to reside in the lower sideband. However, in the upper sideband two H₂CS lines ( $J_{K_-,K_+} = 10_{5,6}\rightarrow 9_{5,5}$ and $J_{K_-,K_+} = 10_{5,5}\rightarrow 9_{5,4}$) at 343.202331 GHz coincide with the position of the CS line in the lower sideband. To check the possibility that these transitions contribute significantly to the observed intensity of the line, a LTE jump-model was run using the parameters derived previously for H₂CS. It is indeed found that these high lying energy levels ( $E_{\rm u} = 418$ K) are sufficiently excited to account for all of the flux observed in this line.