Whereas the presence of a B-mode, and an additional contribution to
the E-mode due to source clustering must occur, one needs to estimate
the relative amplitude of this effect as compared to the "usual''
cosmic shear strength described by ![]() .
This estimate requires
a model for the source clustering, i.e., a model for the function
.
This estimate requires
a model for the source clustering, i.e., a model for the function
![]() .
g can be related to the three-dimensional correlation
function
.
g can be related to the three-dimensional correlation
function
![]() of galaxies,
of galaxies,
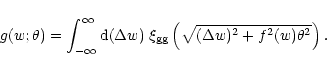 |
(65) |
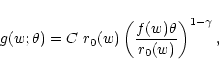 |
(66) |
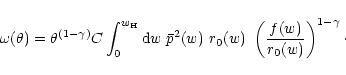 |
(67) |
For this reason, we shall assume the power-law dependence of
![]() as given above; in addition, we will make the
simplifying assumption that the comoving clustering length r0(w) is
independent of distance w; this assumption is not too
critical, since the function
as given above; in addition, we will make the
simplifying assumption that the comoving clustering length r0(w) is
independent of distance w; this assumption is not too
critical, since the function
![]() is relatively
well peaked and therefore large w-variations of the correlation
length are not probed. Then, (69) determines this constant
comoving correlation length r0. We obtain in this case
is relatively
well peaked and therefore large w-variations of the correlation
length are not probed. Then, (69) determines this constant
comoving correlation length r0. We obtain in this case
![\begin{displaymath}g(w;\theta)=\omega(\theta){[f(w)]^{1-\gamma} \over
\int{\rm d} w'~\bar p^2 (w')~[f(w)]^{1-\gamma} }\cdot
\end{displaymath}](/articles/aa/full/2002/27/aah3374/img256.gif)
In order to make further progress, we need to assume a redshift
distribution for the sources from which the shear is measured. We
employ the form (Brainerd et al. 1996)
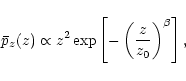 |
(69) |
In Fig. 2 we show an example of the various power spectra
considered here; all power spectra are multiplied by ![]() to
obtain dimensionless quantities. For this figure, we employed a
standard
to
obtain dimensionless quantities. For this figure, we employed a
standard ![]() CDM model with
CDM model with
![]() and
and
![]() and normalization
and normalization
![]() .
Sources are distributed
in redshift according to the foregoing prescription, with z0=1. The
amplitude of the angular correlation function of galaxies was chosen
to be
A(1')=0.02, and the slope of
.
Sources are distributed
in redshift according to the foregoing prescription, with z0=1. The
amplitude of the angular correlation function of galaxies was chosen
to be
A(1')=0.02, and the slope of
![]() for the
three-dimensional correlation function was used; the corresponding
correlation length in this case is
for the
three-dimensional correlation function was used; the corresponding
correlation length in this case is
![]() .
To calculate the three-dimensional power spectrum and its redshift
evolution, we used the Peacock & Dodds (1996) prescription for the
non-linear evolution of
.
To calculate the three-dimensional power spectrum and its redshift
evolution, we used the Peacock & Dodds (1996) prescription for the
non-linear evolution of
![]() .
.
The power spectrum of the projected mass density,
![]() ,
is
the same as that in SvWJK, except for a slightly different choice of
the cosmological parameters. The spectrum
,
is
the same as that in SvWJK, except for a slightly different choice of
the cosmological parameters. The spectrum
![]() is very much
smaller than
is very much
smaller than
![]() ,
as expected from the smallness of the
amplitude of the angular correlation function; in fact, the ratio
,
as expected from the smallness of the
amplitude of the angular correlation function; in fact, the ratio
![]() is nearly constant at a value of
approximately
(1+B)A(1'), with
is nearly constant at a value of
approximately
(1+B)A(1'), with
![]() for this choice of the
parameters.
for this choice of the
parameters.
The behavior of the power spectra which arise from source clustering,
![]() and
and
![]() ,
as a function of
,
as a function of ![]() is quite different. First, both of these spectra are very similar,
which is due to the fact that the J4-term in (61)
is much smaller than the J0-term. Second, although both of
these spectra are small on large angular scales, i.e. at small
is quite different. First, both of these spectra are very similar,
which is due to the fact that the J4-term in (61)
is much smaller than the J0-term. Second, although both of
these spectra are small on large angular scales, i.e. at small ![]() ,
their relative value increases strongly for smaller angular
scales. Hence, as expected, the relative importance of source
clustering increases for larger
,
their relative value increases strongly for smaller angular
scales. Hence, as expected, the relative importance of source
clustering increases for larger ![]() .
What is surprising, though, is
that these power spectra have the same amplitude as
.
What is surprising, though, is
that these power spectra have the same amplitude as ![]() at a
value of
at a
value of
![]() ,
corresponding to an angular scale
of
,
corresponding to an angular scale
of
![]() ,
and the relative contribution of the
B-mode amounts to about 2% at an angular scale of 1'. It should be
noted here that cosmic shear has already been measured on scales below
1'; therefore, source clustering gives rise to a B-mode component in
cosmic shear which is observable.
,
and the relative contribution of the
B-mode amounts to about 2% at an angular scale of 1'. It should be
noted here that cosmic shear has already been measured on scales below
1'; therefore, source clustering gives rise to a B-mode component in
cosmic shear which is observable.
We shall now consider the behavior of
![]() for large
values of
for large
values of ![]() .
The aforementioned properties of
.
The aforementioned properties of
![]() can be summarized as
can be summarized as
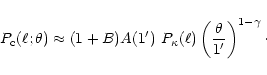
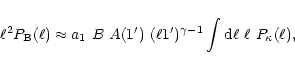
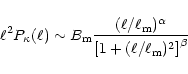
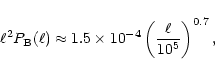
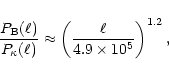
![\begin{figure}
\par\includegraphics[width=7cm,clip]{fig3.tps}\end{figure}](/articles/aa/full/2002/27/aah3374/Timg292.gif) |
Figure 3:
For the same model as in Fig. 2, several correlation
functions are plotted. The solid line shows
|
In Fig. 3 we have plotted several correlation functions; they have
been calculated from the power spectra plotted in Fig. 2 by using (20). The first point to note is that
![]() differs from
differs from ![]() by less than 1% for angular scales larger than 3''; hence, the relative contribution caused by the source
correlation is even smaller than that seen in the power spectra. This
is due to the fact that the correlation function is a filtered version
of the power spectra, however with a very broad filter. This implies
that even at small
by less than 1% for angular scales larger than 3''; hence, the relative contribution caused by the source
correlation is even smaller than that seen in the power spectra. This
is due to the fact that the correlation function is a filtered version
of the power spectra, however with a very broad filter. This implies
that even at small ![]() scales, the correlation function is not
dominated by large values of
scales, the correlation function is not
dominated by large values of ![]() ,
where the contribution from source
clustering is largest, but low values of
,
where the contribution from source
clustering is largest, but low values of ![]() contribute
significantly. The influence of source clustering on the "-'' modes
is larger, since the filtering function for those are narrower (i.e.,
J4(x) is a more localized function that J0(x)), and
contribute
significantly. The influence of source clustering on the "-'' modes
is larger, since the filtering function for those are narrower (i.e.,
J4(x) is a more localized function that J0(x)), and
![]() differs from
differs from ![]() appreciably on scales below about
1'.
appreciably on scales below about
1'.
Finally, in Fig. 4 we have plotted the aperture measures. On scales
below about 1', the dispersion of ![]() is larger than about 1% of
that of
is larger than about 1% of
that of
![]() .
Hence, the ratio of these E- and B-mode aperture
measures are very similar to that of the corresponding power spectra.
.
Hence, the ratio of these E- and B-mode aperture
measures are very similar to that of the corresponding power spectra.
![\begin{figure}
\par\includegraphics[width=7cm]{fig4.tps}\end{figure}](/articles/aa/full/2002/27/aah3374/Timg293.gif) |
Figure 4:
Aperture measures, for the same model as used in Fig. 2. Shown here is the dispersion of the aperture mass,
|
The fact that
![]() and
and ![]() are very similar in
amplitude means that by measuring
are very similar in
amplitude means that by measuring ![]() ,
one can make an
approximate correction of
,
one can make an
approximate correction of ![]() ,
obtaining a value close to
,
obtaining a value close to
![]() by subtracting
by subtracting ![]() from
from ![]() .
Owing to the
relative amplitude of these correlation-induced powers, such a
correction may be needed in future high-precision measurements of the
cosmic shear.
.
Owing to the
relative amplitude of these correlation-induced powers, such a
correction may be needed in future high-precision measurements of the
cosmic shear.
Copyright ESO 2002