

Up: B-modes in cosmic shear
Subsections
In the previous section we have presented the decomposition of a
general shear field into E/B-modes. It is usually assumed that lensing
alone yields a pure E-mode shear field, so that the detection of a
B-mode in the van Waerbeke et al. (2001) data (see also Pen et al. 2002) was surprising and interpreted as being due to systematic errors
or a signature of intrinsic alignment of sources. Here we show that
lensing indeed does generate a B-mode component of the shear if
the source galaxies from which the shear is measured are clustered.
Define the "equivalent'' surface mass density for a fixed source
redshift, or comoving distance w,
![\begin{displaymath}%
\kappa(\vec\theta,w)=
\int_0^w {\rm d} w'\; F(w',w)\;
\delta[f(w')\vec\theta,w']
\end{displaymath}](/articles/aa/full/2002/27/aah3374/img187.gif) |
(43) |
where
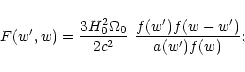 |
(44) |
here, H0 and 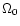 denote the Hubble constant and the density
parameter, w is the comoving distance, f(w) is the comoving
angular-diameter distance to comoving distance w,
denote the Hubble constant and the density
parameter, w is the comoving distance, f(w) is the comoving
angular-diameter distance to comoving distance w, 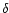 is the
density contrast, and
a(w)=(1+z)-1 is the cosmic scale factor,
defined such that a=1 today, again using the notation of BS01.
Accordingly, we define the shear components
is the
density contrast, and
a(w)=(1+z)-1 is the cosmic scale factor,
defined such that a=1 today, again using the notation of BS01.
Accordingly, we define the shear components
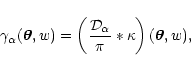 |
(45) |
where the operator 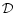 is defined in (1) and (2).
Then, the shear correlation function for two sources at positions
is defined in (1) and (2).
Then, the shear correlation function for two sources at positions
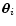 and distances wi becomes
and distances wi becomes
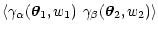 |
= |
![$\displaystyle \left( {\cal D}_\alpha {\cal D}_\beta\over \pi^2 \right) *
\int_0...
...elta[f(w_1')\vec\theta_1,w_1']\;\delta[f(w_2')\vec\theta_2,w_2'] \right\rangle,$](/articles/aa/full/2002/27/aah3374/img194.gif) |
|
where the first 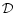 operates on
operates on
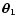 ,
and the second
,
and the second 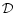 on
on
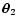 .
This equation is of the form (BS 2.78), and thus we obtain, using
(BS 2.82),
.
This equation is of the form (BS 2.78), and thus we obtain, using
(BS 2.82),
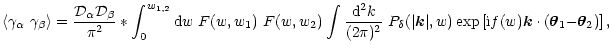 |
|
|
(46) |
where we have temporarily dropped the arguments of the shear
correlator,
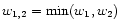 ,
and
,
and 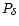 is the power
spectrum of the density fluctuations which develops as a function of
cosmic time (or as a function of comoving distance w). The upper
limit of the integral expresses the fact that a correlated shear can
only be generated by matter which is at smaller distance than both
sources.
is the power
spectrum of the density fluctuations which develops as a function of
cosmic time (or as a function of comoving distance w). The upper
limit of the integral expresses the fact that a correlated shear can
only be generated by matter which is at smaller distance than both
sources.
The operators 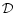 only act on the final term of (47) which
can be evaluated using the Fourier transform of
only act on the final term of (47) which
can be evaluated using the Fourier transform of 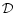 ,
as in (11),
,
as in (11),
so that
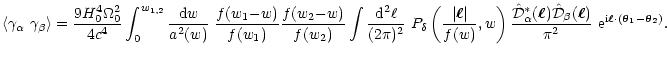 |
|
|
(47) |
Evaluating the relevant combinations, one finds
where
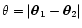 and
R(w,wi)=f(wi-w)/f(wi) is the ratio of the angular diameter
distances of a source at wi seen from the distance
and
R(w,wi)=f(wi-w)/f(wi) is the ratio of the angular diameter
distances of a source at wi seen from the distance 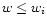 and
that seen from an observer at w=0.
and
that seen from an observer at w=0.
When measuring cosmic shear from source ellipticities, the source
galaxies have a broad distribution in redshift, unless information on
the redshifts are available and taken into account. Hence, to
calculate the observable shear correlation functions, the
foregoing expressions need to be averaged over the source redshift
distribution. Let
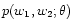 be the probability density for
comoving distances of two sources separated by an angle
be the probability density for
comoving distances of two sources separated by an angle 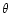 on
the sky; then we have for the observable correlation functions
on
the sky; then we have for the observable correlation functions
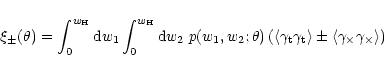 |
(48) |
and 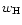 is the comoving distance to the horizon.
By changing the order of integration according to
is the comoving distance to the horizon.
By changing the order of integration according to
we obtain
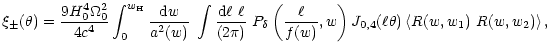 |
|
|
(49) |
where the angular brackets denote the averaging of the
angular-diameter distance ratios over the source distance
distribution.
We shall write the source redshift distribution as
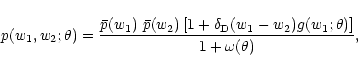 |
(50) |
where
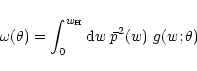 |
(51) |
is the angular correlation function of the galaxies, and 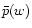 describes their redshift distribution. The second term in (51) accounts for source clustering. In making this ansatz,
we have accounted for the fact that redshift clustering occurs only
over a very small interval in redshift over which all the other
redshift-dependent functions occurring in (50) can be
considered constant. Note that (51) is normalized,
describes their redshift distribution. The second term in (51) accounts for source clustering. In making this ansatz,
we have accounted for the fact that redshift clustering occurs only
over a very small interval in redshift over which all the other
redshift-dependent functions occurring in (50) can be
considered constant. Note that (51) is normalized,
as required. Then, the average of the angular-diameter distance
ratios becomes
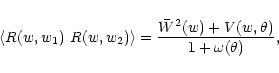 |
(52) |
where
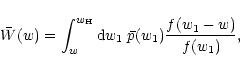 |
(53) |
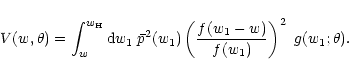 |
(54) |
The correlation of sources thus yields an average of the
angular-diameter distance ratios which is not simply the square of the
mean distance ratio 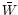 ,
but contains in addition a correlated
part described by V and the normalization correction
,
but contains in addition a correlated
part described by V and the normalization correction 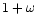 .
If
the angular separation of the sources is large, the correlation in
redshift is expected to be small; hence, for large separations one
expects V and
.
If
the angular separation of the sources is large, the correlation in
redshift is expected to be small; hence, for large separations one
expects V and 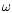 to vanish. The degree of redshift correlation
depends on the angular separation considered; the fact that the mean
of the product of the angular diameter distance ratio (53)
depends on the separation
to vanish. The degree of redshift correlation
depends on the angular separation considered; the fact that the mean
of the product of the angular diameter distance ratio (53)
depends on the separation 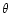 is the cause for a B-mode
contribution to the shear correlation function!
is the cause for a B-mode
contribution to the shear correlation function!
One can check that the correlated redshift probability distribution
behaves as expected in some simple cases. For example, if
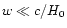 is very much smaller than the characteristic source distance w0,
one finds that
is very much smaller than the characteristic source distance w0,
one finds that
in this case, the lensing strength of matter at distance w is
basically independent of the exact source redshift, so that source
redshift clustering is irrelevant for those lens redshifts. Another
case of interest occurs when the selected sources come from a very
narrow distance interval, of width 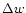 centered on w0; then, (52) yields the relation
centered on w0; then, (52) yields the relation
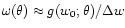 ,
and
,
and
Hence, also in this case,
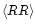 does not depend on
does not depend on 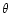 ,
and
therefore no B-mode contribution occurs - as noted before, if all
sources are at the same redshift, one obtains a pure E-mode shear
field.
,
and
therefore no B-mode contribution occurs - as noted before, if all
sources are at the same redshift, one obtains a pure E-mode shear
field.
We can now rewrite (50) in the form
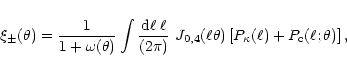 |
(55) |
where the 0 (4) corresponds to 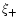 (
(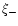 ),
),
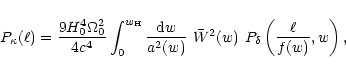 |
(56) |
and
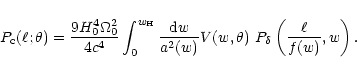 |
(57) |
The first term of (56) in the absence of source correlations
(i.e., 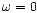 )
is the one usually derived in cosmic shear
considerations;
)
is the one usually derived in cosmic shear
considerations; 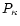 is the power spectrum of the projected
matter density, related to the three-dimensional power spectrum
is the power spectrum of the projected
matter density, related to the three-dimensional power spectrum
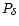 by a Limber-type equation (e.g., Kaiser 1992). The second
term in (56) and the "normalization correction''
by a Limber-type equation (e.g., Kaiser 1992). The second
term in (56) and the "normalization correction'' 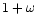 comes about due to source correlations.
comes about due to source correlations.
From the correlation functions (56), by writing
we can derive the
E- and B-mode power spectra, making use of (19),
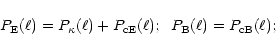 |
(59) |
with
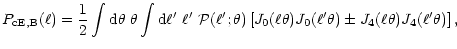 |
|
|
(60) |
where the "+'' ("-'')-sign corresponds to the E- (B-) mode. If the
ratio containing the power spectra did not depend on 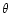 ,
,
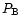 would vanish identically, as it should. However, this term
does depend on
would vanish identically, as it should. However, this term
does depend on  due to source correlations; therefore,
without using redshift information, the presence of B-modes in cosmic
shear observations is unavoidable.
due to source correlations; therefore,
without using redshift information, the presence of B-modes in cosmic
shear observations is unavoidable.
Using the definitions of the E- and B-mode correlation function, we
obtain


Up: B-modes in cosmic shear
Copyright ESO 2002
![\begin{displaymath}%
\kappa(\vec\theta,w)=
\int_0^w {\rm d} w'\; F(w',w)\;
\delta[f(w')\vec\theta,w']
\end{displaymath}](/articles/aa/full/2002/27/aah3374/img187.gif)
![$\displaystyle \left( {\cal D}_\alpha {\cal D}_\beta\over \pi^2 \right) *
\int_0...
...elta[f(w_1')\vec\theta_1,w_1']\;\delta[f(w_2')\vec\theta_2,w_2'] \right\rangle,$](/articles/aa/full/2002/27/aah3374/img194.gif)
![]() only act on the final term of (47) which
can be evaluated using the Fourier transform of
only act on the final term of (47) which
can be evaluated using the Fourier transform of ![]() ,
as in (11),
,
as in (11),
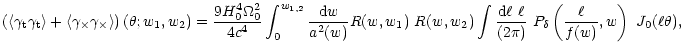
![]() be the probability density for
comoving distances of two sources separated by an angle
be the probability density for
comoving distances of two sources separated by an angle ![]() on
the sky; then we have for the observable correlation functions
on
the sky; then we have for the observable correlation functions
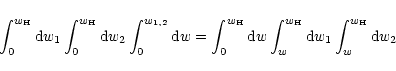
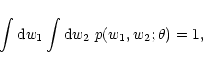
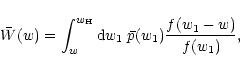
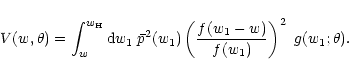
![]() is very much smaller than the characteristic source distance w0,
one finds that
is very much smaller than the characteristic source distance w0,
one finds that
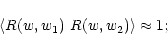
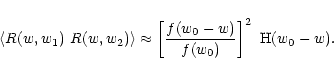
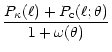
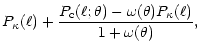
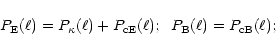
![$\displaystyle %
\xi_{\rm E+}(\theta)=\int{{\rm d} \ell\;\ell\over (2\pi)}~P_\ka...
...)
\left( {4\over {\vartheta}^2}-{12\theta^2\over {\vartheta}^4} \right)\Biggr],$](/articles/aa/full/2002/27/aah3374/img238.gif)
![$\displaystyle \xi_{\rm B+}(\theta)=\int{{\rm d} \ell\;\ell\over (4\pi)}
\Biggl[...
...)
\left( {4\over {\vartheta}^2}-{12\theta^2\over {\vartheta}^4} \right)\Biggr],$](/articles/aa/full/2002/27/aah3374/img239.gif)
![$\displaystyle \xi_{\rm E-}(\theta)=\int{{\rm d} \ell\;\ell\over (2\pi)}~P_\kapp...
...heta})
\left( {4\over \theta^2}-{12{\vartheta}^2\over \theta^4} \right)\Biggr],$](/articles/aa/full/2002/27/aah3374/img240.gif)
![$\displaystyle \xi_{\rm B-}(\theta)=\int{{\rm d} \ell\;\ell\over (4\pi)}
\Biggl[...
...})
\left( {4\over \theta^2}-{12{\vartheta}^2\over \theta^4} \right)\Biggr]\cdot$](/articles/aa/full/2002/27/aah3374/img241.gif)