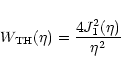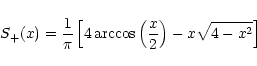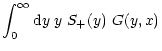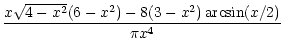Up: B-modes in cosmic shear
Subsections
In this section we provide the basic relations for the decomposition
of the shear field into E- and B-modes. Most of these relations
have been obtained in C01; we shall write them here in standard
lensing notation.
If the shear field is obtained from a projected surface mass density
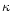 as in Eq. (1), then the gradient of the density
field
as in Eq. (1), then the gradient of the density
field 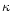 is related to the first spatial derivatives of the
shear components in the following way (Kaiser 1995):
is related to the first spatial derivatives of the
shear components in the following way (Kaiser 1995):
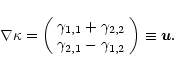 |
(3) |
The vector field 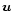 can be obtained from observations, e.g. in
weak lensing cluster mass reconstructions, by obtaining a smoothed
version of the shear field and then differentiating this
numerically. Owing to noise, the resulting ("observed'') field
can be obtained from observations, e.g. in
weak lensing cluster mass reconstructions, by obtaining a smoothed
version of the shear field and then differentiating this
numerically. Owing to noise, the resulting ("observed'') field 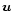 will in general not be a gradient field. The non-gradient part of
will in general not be a gradient field. The non-gradient part of 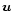 is then a readily identifiable noise component and can be filtered
out in the mass reconstruction. Seitz & Schneider (1996) provided a
scheme for this noise filtering (see also Seitz & Schneider 2001 for
a simpler though equivalent method), which was shown by Lombardi &
Bertin (1998) to be an optimal reconstruction method.
is then a readily identifiable noise component and can be filtered
out in the mass reconstruction. Seitz & Schneider (1996) provided a
scheme for this noise filtering (see also Seitz & Schneider 2001 for
a simpler though equivalent method), which was shown by Lombardi &
Bertin (1998) to be an optimal reconstruction method.
If the shear field cannot be ascribed to a single geometrically thin
gravitational lens, the non-gradient part of 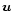 is not
necessarily due to noise. For example, if the galaxies have intrinsic
alignments, this may induce a curl-part of
is not
necessarily due to noise. For example, if the galaxies have intrinsic
alignments, this may induce a curl-part of 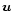 .
To project out the
gradient and curl part of
.
To project out the
gradient and curl part of 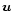 ,
we take a further derivative
of
,
we take a further derivative
of 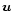 ,
and define
,
and define
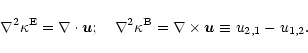 |
(4) |
Through these relations,
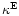 and
and
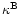 are not
uniquely defined on a finite data field; as discussed in Seitz &
Schneider (1996), a further condition is needed to specify the two
modes uniquely. However, we shall not be concerned here with
finite-field effects.
are not
uniquely defined on a finite data field; as discussed in Seitz &
Schneider (1996), a further condition is needed to specify the two
modes uniquely. However, we shall not be concerned here with
finite-field effects.
An alternative way to define
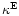 and
and
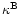 is
through the Kaiser & Squires (1993) mass-reconstruction relation
is
through the Kaiser & Squires (1993) mass-reconstruction relation
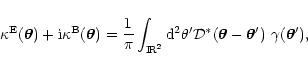 |
(5) |
which formally requires data on an infinite field; here,
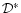 denotes the complex-conjugate of the complex kernel (2). If
denotes the complex-conjugate of the complex kernel (2). If
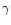 is of the form (1) with a real field
is of the form (1) with a real field 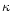 ,
then the result from (5) will be real,
,
then the result from (5) will be real,
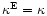 ,
,
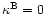 .
In applications of the KS-formula (5) to observational data, where the recovered shear field
necessarily is noisy, one usually takes the real part of the integral
to obtain the projected mass density field. For a general shear field,
the result from (5) will be complex, with the real part
yielding the E-mode, and the imaginary part corresponding to the
B-mode.
.
In applications of the KS-formula (5) to observational data, where the recovered shear field
necessarily is noisy, one usually takes the real part of the integral
to obtain the projected mass density field. For a general shear field,
the result from (5) will be complex, with the real part
yielding the E-mode, and the imaginary part corresponding to the
B-mode.
To simplify notation and calculations, it is convenient to express
two-component quantities in terms of complex numbers. We define the E-
and B-mode potentials
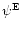 and
and
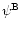 by
by
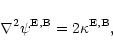 |
(6) |
and combine the two modes into the complex fields
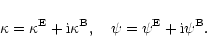 |
(7) |
The complex shear
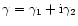 is obtained from
the potential
is obtained from
the potential 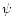 by
by
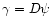 ,
where the differential
operator
,
where the differential
operator
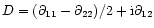 ;
hence,
;
hence,
Inserting this into (3) yields
Indeed, the shear field can be decomposed into E/B-modes,
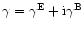 ,
with
,
with
where the operator 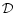 is defined in Eqs. (1), (2), and "*'' denotes complex conjugation. Thus, the two
components can be obtained from the shear field by filtering, except
for an additive constant.
is defined in Eqs. (1), (2), and "*'' denotes complex conjugation. Thus, the two
components can be obtained from the shear field by filtering, except
for an additive constant.
The discussion above dealt with the shear field itself. In the
application to cosmic shear, one usually does not investigate the
shear of a 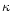 -field itself, but its statistical properties. In
this paper we shall concentrate solely on two-point statistical
measures of the cosmic shear, and their decomposition into E- and
B-modes.
-field itself, but its statistical properties. In
this paper we shall concentrate solely on two-point statistical
measures of the cosmic shear, and their decomposition into E- and
B-modes.
Owing to statistical homogeneity and isotropy of the Universe,
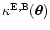 are homogeneous and isotropic random
fields. Hence, in terms of their Fourier transforms
are homogeneous and isotropic random
fields. Hence, in terms of their Fourier transforms
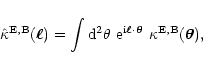 |
(8) |
one defines the two power spectra 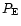 ,
,
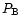 ,
and the
cross power spectrum
,
and the
cross power spectrum
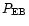 by
by
where
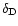 denotes Dirac's delta distribution.
In terms of the complex field
denotes Dirac's delta distribution.
In terms of the complex field 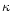 ,
we then have
,
we then have
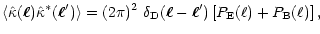 |
|
|
|
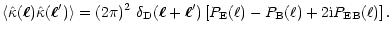 |
|
|
(10) |
The Fourier transform
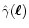 of the shear is related to
of the shear is related to
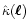 through
through
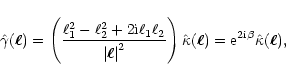 |
(11) |
where 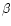 is the polar angle of
is the polar angle of 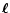 .
The correlators of the
shear then become
.
The correlators of the
shear then become
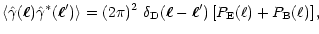 |
|
|
|
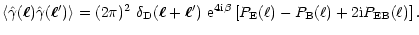 |
|
|
(12) |
Next we define the correlation functions of the shear. This is done by
considering pairs of positions
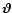 and
and
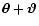 ,
and
defining the tangential and cross-component of the shear at position
,
and
defining the tangential and cross-component of the shear at position
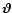 for this pair as
for this pair as
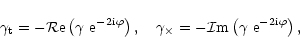 |
(13) |
respectively, where 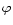 is the polar angle of the separation vector
is the polar angle of the separation vector
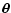 .
Then, the shear correlation functions are defined as
.
Then, the shear correlation functions are defined as
The shear correlation functions are most easily calculated by choosing
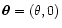 ,
in which case
,
in which case
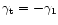 ,
,
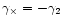 ,
and expressing the shear in terms of its
Fourier modes,
,
and expressing the shear in terms of its
Fourier modes,
Making use of the orthogonality of Bessel functions,
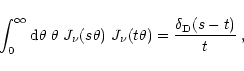 |
(17) |
we can invert the relations (15) and (16) and
express the power spectra in terms of the correlation functions,
Hence, we have now expressed the various power spectra in terms of the
directly observable correlation functions 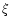 .
One notes that the
correlation functions
.
One notes that the
correlation functions 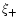 and
and 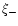 depend on both, the E- and
B-mode power spectra, whereas the cross-correlation
depend on both, the E- and
B-mode power spectra, whereas the cross-correlation
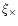 depends on the cross-power
depends on the cross-power
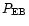 only. It is obvious that the
cross-power and its corresponding correlation function do not "mix in''
with the E- and B-mode; in addition, the cross-power vanishes if the
shear field is statistically invariant under parity transformations,
which leave
only. It is obvious that the
cross-power and its corresponding correlation function do not "mix in''
with the E- and B-mode; in addition, the cross-power vanishes if the
shear field is statistically invariant under parity transformations,
which leave
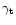 unchanged, but transform
unchanged, but transform
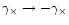 .
One can therefore assume that in
realistic cases,
.
One can therefore assume that in
realistic cases,
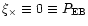 .
However, since
cosmic shear is measured from finite data fields, cosmic variance may
lead to a non-zero measurement of the cross-power; in fact, the
measurement of the cross-power may serve as a lower limit on error bars
of the other power spectra.
For a determination of the power spectra, the expressions (19) require a measurement of the correlation functions over
an infinite range in angle; whereas the
correlation functions decrease with
.
However, since
cosmic shear is measured from finite data fields, cosmic variance may
lead to a non-zero measurement of the cross-power; in fact, the
measurement of the cross-power may serve as a lower limit on error bars
of the other power spectra.
For a determination of the power spectra, the expressions (19) require a measurement of the correlation functions over
an infinite range in angle; whereas the
correlation functions decrease with 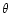 and become very small for
large
and become very small for
large 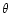 ,
so that in effect the integrals can be replaced by
ones over a finite range of integration, one might want to obtain more
local decompositions into E- and B-modes.
,
so that in effect the integrals can be replaced by
ones over a finite range of integration, one might want to obtain more
local decompositions into E- and B-modes.
We define the four correlation functions
which are defined such that in the absence of B-modes,
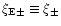 ;
these four correlation functions have also been
defined in C01, although only the "+'' ones were investigated in more
detail there. Inserting (19) into the
foregoing definitions, one obtains
;
these four correlation functions have also been
defined in C01, although only the "+'' ones were investigated in more
detail there. Inserting (19) into the
foregoing definitions, one obtains
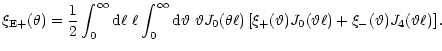 |
|
|
(20) |
The 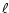 -integration can be carried out; consider the function
-integration can be carried out; consider the function
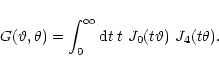 |
(21) |
Making use of the recurrence relations for Bessel functions, one
can express J4 as
By using Eq. (11.4.41) of Abramowitz & Stegun (1965), together with (18), one can perform the integration in (22) term by
term to obtain
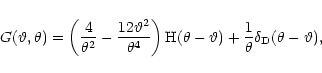 |
(22) |
where
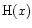 is the Heaviside step function. We also note the
interesting property,
is the Heaviside step function. We also note the
interesting property,
which is readily shown using (18).
Thus, (21) becomes
We have obtained a combination of shear correlation functions
which depends only on the E-modes; however, in order to obtain
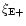 one would need to know
one would need to know 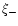 for arbitrarily large
separations. However,
for arbitrarily large
separations. However,
depends on the observable correlation functions 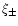 over a
finite range only and thus can be measured from finite data sets.
Analogously, we find for the B-mode correlation functions
over a
finite range only and thus can be measured from finite data sets.
Analogously, we find for the B-mode correlation functions
We note that
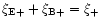 ,
,
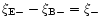 .
In order to calculate the E- and B-mode correlation
functions, one needs to know either the observable correlation
function
.
In order to calculate the E- and B-mode correlation
functions, one needs to know either the observable correlation
function 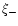 to arbitrarily large, or
to arbitrarily large, or 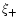 to arbitrarily small
separations. This is of course impossible, owing to the finite size of
data fields on the one hand, and the impossibility to measure shapes
of very close pairs of galaxies. In either case, the lack of
measurements for large (or small) separations can be summarized in two
constants: suppose that
to arbitrarily small
separations. This is of course impossible, owing to the finite size of
data fields on the one hand, and the impossibility to measure shapes
of very close pairs of galaxies. In either case, the lack of
measurements for large (or small) separations can be summarized in two
constants: suppose that 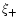 can be measured down to separations of
can be measured down to separations of
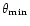 ;
then, the integral in the "-'' modes over
;
then, the integral in the "-'' modes over 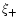 can be split into one from 0 to
can be split into one from 0 to
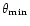 ,
and one from
,
and one from
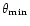 to
to 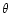 .
The former one has the
.
The former one has the
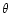 -dependence
-dependence
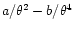 ,
where a, b are two
constants, depending on
,
where a, b are two
constants, depending on 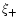 for
for
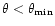 .
The
decline of this contribution, with leading order
.
The
decline of this contribution, with leading order
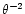 ,
shows
that it has a small influence on the determination of the "-'' modes
for
,
shows
that it has a small influence on the determination of the "-'' modes
for
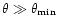 ;
in addition, "reasonable guesses''
for a and b may be obtained by extrapolating the measured
;
in addition, "reasonable guesses''
for a and b may be obtained by extrapolating the measured 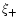 towards small angles. The same reasoning shows the analogous
situation for the "+'' modes.
towards small angles. The same reasoning shows the analogous
situation for the "+'' modes.
One very convenient way to separate E- and B-modes is provided by the
aperture mass: defining the tangential and cross component of the shear
relative to the center of a circular aperture of angular radius
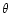 ,
and defining
,
and defining
it was shown in C01 that E-modes do not contribute to 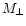 ,
and
B-modes do not contribute to
,
and
B-modes do not contribute to
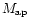 ;
in fact, this can be easily
seen directly by inserting the Fourier transform of the shear (11) into (28). Here,
;
in fact, this can be easily
seen directly by inserting the Fourier transform of the shear (11) into (28). Here,
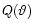 is an
axially-symmetric weight function which can be chosen arbitrarily. The
integration range in the foregoing equations extends over the support
of the weight function Q. The aperture mass was introduced by
Schneider (1996) in an attempt to detect mass peaks from shear fields,
and later used by SvWJK as a two- and three-point statistics for
cosmic shear.
is an
axially-symmetric weight function which can be chosen arbitrarily. The
integration range in the foregoing equations extends over the support
of the weight function Q. The aperture mass was introduced by
Schneider (1996) in an attempt to detect mass peaks from shear fields,
and later used by SvWJK as a two- and three-point statistics for
cosmic shear.
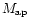 can also be written as a filtered version
of the surface mass density (with a different and compensated weight
function which is related to Q), whereas
can also be written as a filtered version
of the surface mass density (with a different and compensated weight
function which is related to Q), whereas 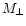 has no direct
physical interpretation; in the absence of B-modes,
has no direct
physical interpretation; in the absence of B-modes, 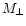 should
vanish, and any non-vanishing signal is usually interpreted as being
due to noise or remaining systematics, and thus as a convenient error
estimate for
should
vanish, and any non-vanishing signal is usually interpreted as being
due to noise or remaining systematics, and thus as a convenient error
estimate for
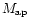 .
In SvWJK, a family of convenient weight
functions Q was considered, the simplest of which is
.
In SvWJK, a family of convenient weight
functions Q was considered, the simplest of which is
where 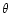 is the radius of the aperture. This form of the weight
function shall be assumed in the following.
is the radius of the aperture. This form of the weight
function shall be assumed in the following.
Using the complex number
where 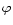 is the polar angle of
is the polar angle of
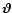 ,
one finds that
,
one finds that
with
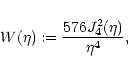 |
(29) |
which was derived by using the Fourier transform (11) of the
shear, and the final steps are as in SvWJK. Similarly, one obtains
Combining the two previous equations, one thus gets
so that these two-point statistics clearly separate E- and B-modes. In
addition, they provide a highly localized measure of the corresponding
power spectra, since the filter function 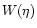 involved is quite narrow (see SvWJK);
in fact, Bartelmann & Schneider (1999) have shown that replacing
involved is quite narrow (see SvWJK);
in fact, Bartelmann & Schneider (1999) have shown that replacing 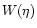 in (32) by
in (32) by
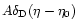 ,
with
,
with
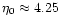 ,
provides a fairly accurate approximation.
Furthermore, (31) can
be used to check whether the shear data contain a contribution from
the cross power
,
provides a fairly accurate approximation.
Furthermore, (31) can
be used to check whether the shear data contain a contribution from
the cross power
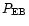 .
.
The aperture measures can be obtained directly from the observational
data by laying down a grid of points, at each of which
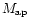 and
and 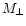 are calculated from (28). However, obtaining
the dispersion with this strategy turns out to be difficult in
practice, since data fields usually contain holes and gaps,
e.g. because of masking (for bright stars), bad columns etc. It is
therefore interesting to calculate these dispersions directly in terms
of the correlation functions, which can be done by inserting (19) into (32),
are calculated from (28). However, obtaining
the dispersion with this strategy turns out to be difficult in
practice, since data fields usually contain holes and gaps,
e.g. because of masking (for bright stars), bad columns etc. It is
therefore interesting to calculate these dispersions directly in terms
of the correlation functions, which can be done by inserting (19) into (32),
where we have defined the functions
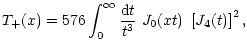 |
|
|
|
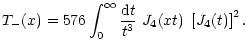 |
|
|
(33) |
The integration range in (33) formally extends from zero to
infinity, but as we shall see shortly, the functions  vanish for
x>2, so the integration range is
vanish for
x>2, so the integration range is
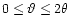 :
for T-(x), an analytic expression can be obtained, using Eq. (6.578.9) of Gradshteyn & Ryzhik (1980),
:
for T-(x), an analytic expression can be obtained, using Eq. (6.578.9) of Gradshteyn & Ryzhik (1980),
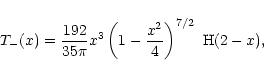 |
(34) |
so that T-(x) vanishes for x>2.
Furthermore, the two functions T+ and T-(x) are related: using
(18), one finds that
so that
T-(x) =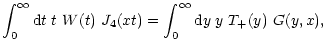 |
|
T+(x) =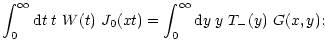 |
|
using the latter expression, together with (35)
and (23), one obtains
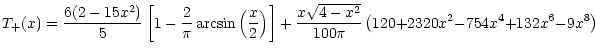 |
|
|
(35) |
for 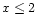 ,
and T+(x) vanishes for x>2. Hence, the integrals in (33) extend only over
,
and T+(x) vanishes for x>2. Hence, the integrals in (33) extend only over
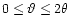 ,
so that
,
so that
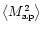 and
and
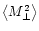 can be obtained directly in
terms of the observable correlation function
can be obtained directly in
terms of the observable correlation function 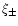 over a finite
interval. The two functions
over a finite
interval. The two functions 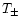 are plotted in Fig. 1.
are plotted in Fig. 1.
![\begin{figure}
\par\includegraphics[width=5.3cm,clip]{fig1.tps}\end{figure}](/articles/aa/full/2002/27/aah3374/Timg176.gif) |
Figure 1:
The four functions defined in text. |
Another cosmic shear statistics often employed is the shear dispersion
in a circle of angular radius 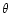 .
It is related to the power
spectra by
.
It is related to the power
spectra by
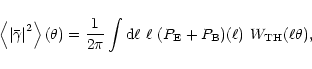 |
(36) |
where
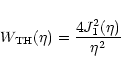 |
(37) |
is the top-hat filter function. In contrast to the aperture measures
of the previous subsection, the shear dispersion (37)
contains both modes; furthermore, the filter function
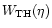 is much broader than
is much broader than 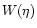 in (30), as
demonstrated in SvWJK. It thus provides a much less localized measure
of the power spectra than the aperture measures. On the other hand,
this larger filter width implies that the signal of the shear
dispersion is larger than that of the aperture measures, which
explains why the first cosmic shear detections (van Waerbeke et al.
2000; Bacon et al. 2001; Kaiser et al. 2000) were obtained in terms
of the shear dispersion.
in (30), as
demonstrated in SvWJK. It thus provides a much less localized measure
of the power spectra than the aperture measures. On the other hand,
this larger filter width implies that the signal of the shear
dispersion is larger than that of the aperture measures, which
explains why the first cosmic shear detections (van Waerbeke et al.
2000; Bacon et al. 2001; Kaiser et al. 2000) were obtained in terms
of the shear dispersion.
As before, the shear dispersion can be obtained by calculating the
mean shear in circles which are laid down on a grid of points, with
the drawback of being affected by gaps in the data
field. Alternatively, the shear dispersion can be obtained directly
from the correlation function,
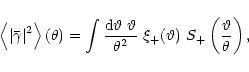 |
(38) |
where (van Waerbeke 2000)
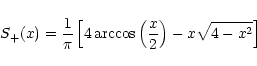 |
(39) |
for 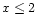 ,
and zero otherwise. Hence, the integral in (39)
extends only over the finite interval
,
and zero otherwise. Hence, the integral in (39)
extends only over the finite interval
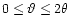 ,
which
makes this a convenient way to calculate the shear dispersion.
,
which
makes this a convenient way to calculate the shear dispersion.
One can also define the shear dispersions of the E- and B-mode,
according to
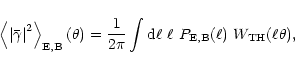 |
(40) |
but they cannot be individually obtained from measuring the shear
directly. Nevertheless, both of these dispersions can be obtained in
terms of the correlation functions,
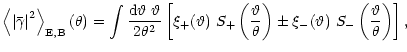 |
|
|
(41) |
which can be derived in close analogy to the derivation of
(33), and the function S- is related to S+ in the same
way as the corresponding T-functions,
| S-(x) |
= |
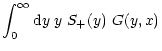 |
|
| |
= |
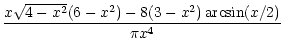 |
(42) |
for 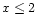 ,
and
S-(x)=4(x2-3)/x4 for x>2. Hence, the
integrals in (42) do not cut off at finite separation, which
was to be expected, since a constant shear cannot be uniquely assigned
to an E- or B-mode, but contributes to
,
and
S-(x)=4(x2-3)/x4 for x>2. Hence, the
integrals in (42) do not cut off at finite separation, which
was to be expected, since a constant shear cannot be uniquely assigned
to an E- or B-mode, but contributes to
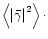


Up: B-modes in cosmic shear
Copyright ESO 2002
![]() as in Eq. (1), then the gradient of the density
field
as in Eq. (1), then the gradient of the density
field ![]() is related to the first spatial derivatives of the
shear components in the following way (Kaiser 1995):
is related to the first spatial derivatives of the
shear components in the following way (Kaiser 1995):
![]() is not
necessarily due to noise. For example, if the galaxies have intrinsic
alignments, this may induce a curl-part of
is not
necessarily due to noise. For example, if the galaxies have intrinsic
alignments, this may induce a curl-part of ![]() .
To project out the
gradient and curl part of
.
To project out the
gradient and curl part of ![]() ,
we take a further derivative
of
,
we take a further derivative
of ![]() ,
and define
,
and define
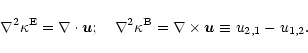
![]() and
and
![]() is
through the Kaiser & Squires (1993) mass-reconstruction relation
is
through the Kaiser & Squires (1993) mass-reconstruction relation
![]() and
and
![]() by
by
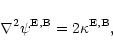
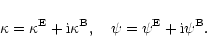
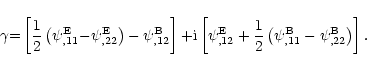
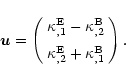
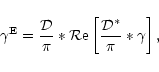
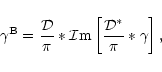
![]() -field itself, but its statistical properties. In
this paper we shall concentrate solely on two-point statistical
measures of the cosmic shear, and their decomposition into E- and
B-modes.
-field itself, but its statistical properties. In
this paper we shall concentrate solely on two-point statistical
measures of the cosmic shear, and their decomposition into E- and
B-modes.
![]() are homogeneous and isotropic random
fields. Hence, in terms of their Fourier transforms
are homogeneous and isotropic random
fields. Hence, in terms of their Fourier transforms
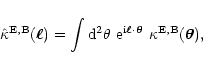
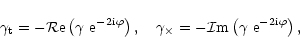
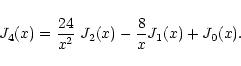
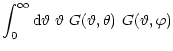
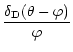
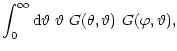
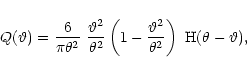
![]() and
and ![]() are calculated from (28). However, obtaining
the dispersion with this strategy turns out to be difficult in
practice, since data fields usually contain holes and gaps,
e.g. because of masking (for bright stars), bad columns etc. It is
therefore interesting to calculate these dispersions directly in terms
of the correlation functions, which can be done by inserting (19) into (32),
are calculated from (28). However, obtaining
the dispersion with this strategy turns out to be difficult in
practice, since data fields usually contain holes and gaps,
e.g. because of masking (for bright stars), bad columns etc. It is
therefore interesting to calculate these dispersions directly in terms
of the correlation functions, which can be done by inserting (19) into (32),
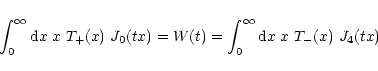
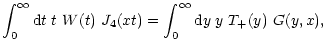
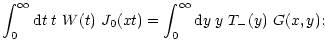
![]() .
It is related to the power
spectra by
.
It is related to the power
spectra by